齿轮箱迷宫密封仿真试验优化

姜紫薇，陈 庆，时 龙

(吉林化工学院 机电工程学院，吉林 吉林 132022)

随着我国高速动车组的不断发展，对其安全性和可靠性的要求也不断提高，传动齿轮箱为动车组列车驱动系统中的传动轴传递动力，是其重要零部件之一.动车在高速行驶时传动轴的转速非常高，这就导致箱内的润滑油油温升高，气压分布不均匀，黏度降低，出现窜油、漏油的现象[1]，会严重影响齿轮箱的密封性能，降低动车的工作效率.为了维持齿轮箱的高速运转和工作中的稳定压力，确保其平稳运行，通常在齿轮箱的轴端采用非接触式迷宫密封[2-3].

如今，针对高速齿轮箱密封特性的研究有很多，并且提出了有关迷宫密封泄漏量的计算方法.焦圳等[4]用CFD方法对三角形、矩形、梯形和圆弧形4组不同的齿形结构进行数值模拟与理论计算对比，得出圆弧形齿结构密封性能最好.巴鹏等[5]利用FLUENT分析了密封间隙对迷宫密封性能的影响，在相同尺寸下，齿间间隙宽度越大，泄漏量越大.贾文聪等[6]利用正交实验模拟计算得到了一些迷宫密封结构参数对泄漏量的影响.原建博等[7]对现今高速齿轮箱密封存在的问题进行了讨论，并指出了未来的发展方向.尹露等[8]研究了迷宫密封在不同腔室、间隙和齿数的动力特性，并对比分析了S-CO2和空气两种不同工作介质对密封稳定性的影响.顾乾磊等[9]通过实验和数值分析模型计算研究了迷宫密封的进口预旋对整体密封稳定性的影响，结果表明正预旋会降低系统稳定性,但对于较少齿数的迷宫密封,正预旋会提高系统稳定性.本文首先通过Fluent对迷宫密封进行模拟计算，再分析端面各个参数对密封性能的影响，找出最优的密封结构.

1 迷宫密封结构及模拟仿真

1.1 建立模型

以高速传动齿轮箱传动轴轴端的迷宫密封为研究对象，利用Creo建立三维模型，如图1～2所示.

图1 迷宫密封三维模型

图2 齿轮箱径向密封结构示意图

半径为65 mm,改变不同的齿顶长度，即2.3、2.5、2.7、2.9 mm，不同齿距为0.5、0.6、0.7、0.8 mm.将模型导入到Fluent中，模拟气体在迷宫密封内的流动情况，并探究改变齿距、齿顶长度、入口压力、转速对迷宫密封性能的影响.

1.2 网格划分

图3为迷宫密封的整体网格划分.使用GAMBIT2.4.2对计算域进行网格划分，首先对整体模型进行区域划分，生成轴向网格，再用平面对齿轮进行径向切分生成面网格，面网格精度控制在0.1 mm，最后整体生成体网格，共1 105 000个四面体单元.

图3 整体结构网格

1.3 Fluent前处理

在Fluent设置中采用标准的k-ε模型，介质用理想可压缩气体来代替正常工作时的油气混合物，压力入口设定为100 Pa，入口温度为375 K，操作压力为环境背压，数值为101 325 Pa，转子壁面为旋转壁面，转速为100 r/min，不考虑壁面与气体间的传热.

1.4 数学模型

由于迷宫密封中流体介质为理想气体，气体流动可认为是二维的稳态湍流流动.根据连续性方程、动量守恒方程和能量守恒方程，其通用微分形式[10]为：

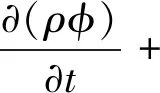
(1)

式中：φ为通用变量；u为速度矢量；Γφ为扩散系数；Sφ为源相.

迷宫密封仿真时湍流模型选用Standardk-ε模型，湍流能k和湍流能耗散率ε的方程[11]分别为：

(2)

(3)

式中：Gk为平均速度梯度引起的湍动能；Gb为浮力引起的湍动能；YM为可压缩流的脉动扩张；Cε1、Cε2、Cε3为常数；σk、σε分别为k、ε的Prandtl数；Sk、Sε为源相.

对于理想气体，其状态方程为

p=ρRT，

(4)

式中：R为气体常数；T为绝对温度.

2 迷宫密封内流场及泄漏量分析

2.1 齿距宽度对泄漏量的影响

通过改变的大小齿距，用Fluent模拟计算得到了其压力分布云图和速度矢量图，如图4～5所示.由图6可知，随着齿距的增大，齿轮箱入口处的压力值不断减小，速度不断增大，泄漏量成线性增加.这是由于迷宫密封进出口压差为定值时，齿距越大，产生的透气现象越严重使得节流作用减弱，泄漏量增大.

图4 不同齿距的压力分布云图

图5 不同齿距的速度矢量图

齿距/mm图6 泄漏量随齿距宽度的变化曲线

2.2 齿顶长度对泄漏量的影响

由图7～9可知，迷宫密封的压差一定时，泄漏量随着齿顶长度的增加先减小然后基本保持不变，内流场的压力最大值随齿顶长度的增大而逐渐增大.

齿顶长度/mm图7 压力随齿顶长度的变化曲线

齿顶长度/mm图8 速度峰值随齿顶长度的变化曲线

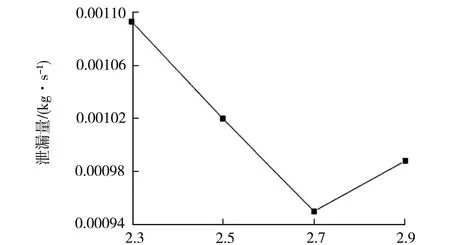
齿顶长度/mm图9 泄漏量随齿顶长度的变化曲线

当齿顶长度为2.7 mm时，密封内流场的空腔内出现了强烈的涡流效应，使泄漏量降到最低，得出2.7 mm是迷宫密封最佳齿顶长度；齿顶长度为2.3 mm时，空腔中的涡流现象不剧烈，导致泄漏量较大；当齿顶长度大于2.7 mm时，空腔中涡流的能量消耗与透气现象到了动态平衡，所以泄漏量变化不大.

2.3 转速对泄漏量的影响

忽略温升的影响，取齿距和齿顶长度为前文模拟得到的最佳参数，即0.5 mm和2.7 mm，入口压力分别为1 000、2 000、3 000、4 000 Pa，转速的取值范围是1 000、2 000、3 000、4 000 r·min-1.转速与入口压力变化对泄漏量的影响如图10所示.

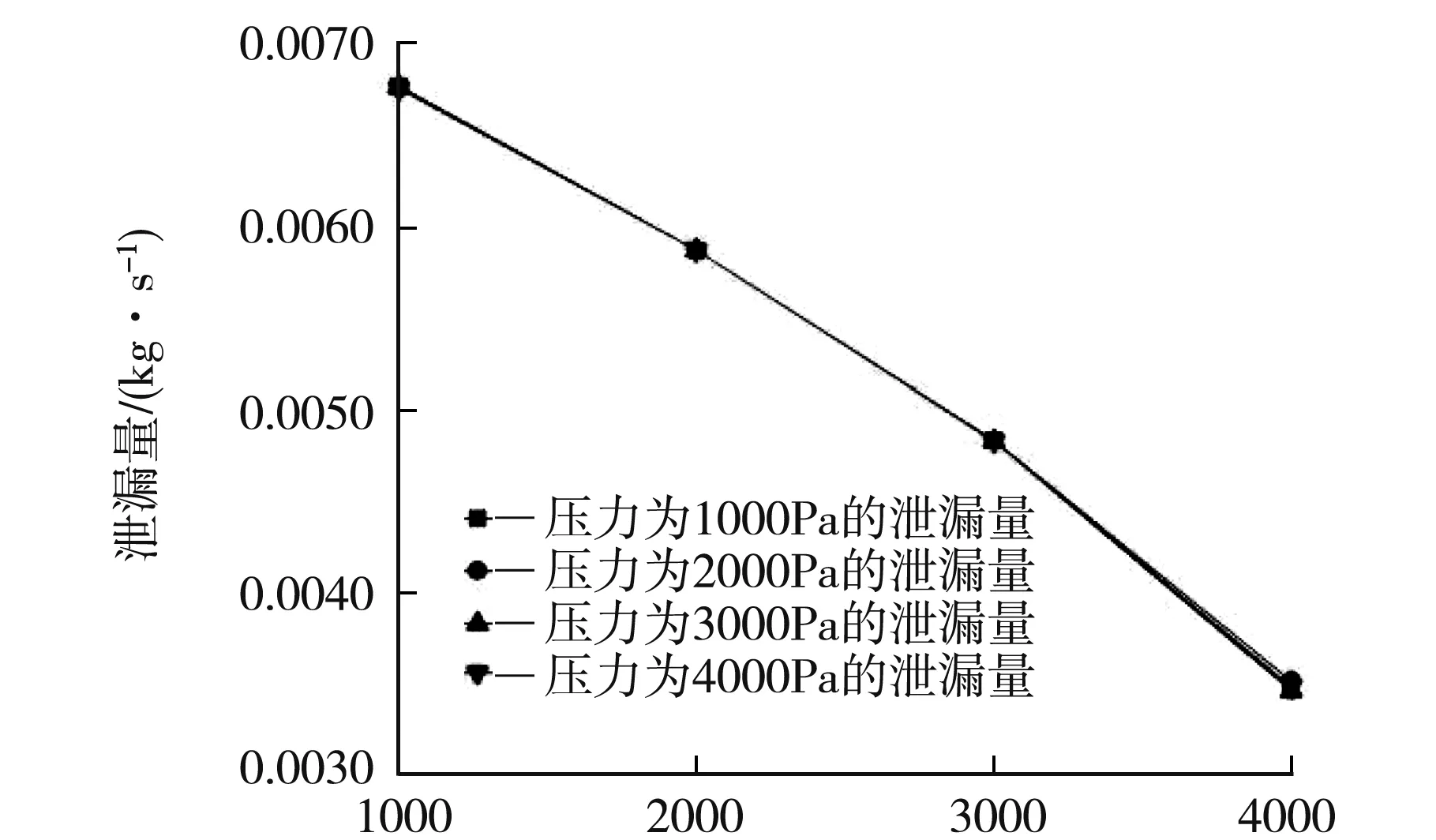
转速/(r·min-1)图10 转速和入口压力对泄漏量的影响

从图10可知，随着转速的增加，泄漏量逐渐增大.这是由于当转速增大时，轴端的周向速度也随之变大，内流场的气流受周向速度影响，气流变成了一条螺旋线，周向速度越大，螺旋线就越长，从而增大了气流的阻力，使泄漏量减小.当齿轮轴转速从1 000 r·min-1增加到4 000 r·min-1时，泄漏量仅减少了0.003，因此转速对泄漏量影响不大.

3 结 论

(1)随着齿距的增大，产生的透气现象越严重使得节流作用减弱，导致泄漏量成线性增加，所以齿距在0.5 mm时较好.

(2)当迷宫密封齿顶长度为2.3 mm时，空腔中的涡流现象不剧烈，导致泄漏量较大；当齿顶长度大于2.7 mm时，空腔中涡流的能量消耗与透气现象到了动态平衡，使得泄漏量变化不大；当齿顶长度为2.7 mm时，迷宫密封的空腔内出现了剧烈的涡流效应，使泄漏量最低，即最佳齿顶长度为2.7 mm.

(3)当转速和入口压力同时增大时周向速度变大，内流场气流受周向速度影响增大了气流流线阻力，所以泄漏量减小，但转速从1 000 r·min-1增加到4 000 r·min-1，泄漏量变化不大，因此得出转速对泄漏量几乎没有影响.