双足机器人节能步态规划算法
2021-06-17卢志强侯媛彬周福娜
卢志强,侯媛彬,孟 芸,周福娜
(1.西安科技大学 机械工程学院,陕西 西安 710054;2.河南大学 计算与信息工程学院,河南 开封 475004)
0 引 言
双足机器人具有类人的结构和外观,可以很好地适应人类的生活环境,是替代人类从事如煤矿救援等危险性工作的理想机器人[1]。人们期待双足机器人能够以类人的方式在现实环境中稳定可靠地行走[2],甚至是奔跑[3]。虽然人类可以相对轻松地执行各种运动,但将人类的行为转化为双足机器人动态运动仍然是一项具有挑战性的任务。近40 a来,国内外研究机构与学者在双足机器人领域进行了许多理论[4]和实验研究[5],并取得显著的发展,如HRP-4可以将车辆行驶在道路中央[6],ATLAS能跨越障碍、攀爬楼梯等[7]。
双足行走问题是双足机器人运动研究中最重要且最根本的问题,按照研究思想的不同,提出双足行走方法可分为3类:其一是以人类行走特征为参考的步态生成方法。双足机器人设计的原型是人类本身,很多研究人员使用高速光学运动捕捉系统获取人体运动的轨迹,分析人类的运动特征,并将这些特征应用到仿人机器人的运动中。BOUTIN等捕捉人体全身运动轨迹,生成双足机器人步行模式,将该方法成功应用于HRP-2和HOAP-3这2款机器人的行走[8]。吴伟国等采集人体髋、腿、踝的运动样本,构建机器人仿人步行样本库,实现机器人与人跟随步行[9]。其二是基于中枢模式发生器(central pattern generator,CPG)的步态生成方法。人类的双足运动具有周期节律性的特征,CPG是能够产生节律运动的神经环路网络,模仿CPG产生节律信号,可控制机器人步行运动。刘成菊等使用脚底压力和腰部加速度作为CPG的驱动,实现了机器人NAO对不同地形的自适应行走[10]。JUANG等使用连续多目标蚁群优化的全连接递归神经网络构成CPG,解决NAO的多目标步态生成问题[11]。其三是基于双足机器人简化模型的步态生成方法。双足机器人一般有几十个自由度且没有固定的基座,导致其动力学系统非常复杂。考虑到系统复杂度和计算复杂度,利用完整的动力学系统模型难以实现双足机器人的步行运动,简化动力学系统便成为实现双足机器人步行运动很好且容易实现的方案。HONG等将仿人机器人简化成一个单质点和可伸缩不计质量的腿构成的线性倒立摆模型[12],SHAFII等将双足机器人简化成一个不计质量桌子与将全部质量集中在一辆在桌面上行驶小车构成的桌子-小车模型[13],SHIMMYO等在单质点倒立摆模型的基础上,进一步考虑了支撑腿和摆动腿质量,构成了三质心倒立摆模型[14]。
目前,已有的双足机器人结构复杂程度还远逊于人类,这决定了以人类特征为参考和基于中枢模式发生器的步态生成方法有其局限性,研究人员更倾向于采用双足机器人简化模型的方法。简化模型的精度决定了控制效果的精度,LUO等在三质心模型中,采用加入角动量的模型预测控制,获得了比单质心模型或一般三质心模型高的零力矩点寻迹精度[15]。另一方面,减少机器人控制中的约束条件能获得更优的控制效果,SHIN等允许机器人身体垂直运动,提高了行走速度、降低了驱动电机的能耗[16]。若允许机器人身体有更多自由度的运动,可以获得更好的控制效果。约束条件的减少,则意味着机器人控制中参数空间的增大,用人工智能的方法寻找最优解将是一个有意义的问题,WRIGHT等综述了机器人运动控制中的常用智能算法[17]。
结合当前双足机器人行走步态规划领域的研究成果和存在的不足,文中提出一种兼顾双足机器人行走稳定性的节能步态规划算法,解决双足机器人行走的步态规划与控制问题。
1 问题陈述
1.1 系统结构
文中使用的双足机器人,具有双臂和双腿,可以模仿人体的行走运动,机器人的每条腿有5个自由度,分别为髋部转角q1/q6,q2/q7,膝盖转角q3/q8,脚踝转角q4/q9和q5/q10,设关节向量q=[q1,q2,…,q10]T。机器人前、侧和垂直方向,分别被定义为X轴、Y轴和Z轴方向。世界坐标系的原点定位于机器人直立时的两脚中点,机器人模型如图1所示。双足机器人每个脚底分别安装4片FSR压力传感器,用来测量脚底作用力的分布,表1列出了机器人身体及右腿的质量及长度,机器人左腿的参数相同。
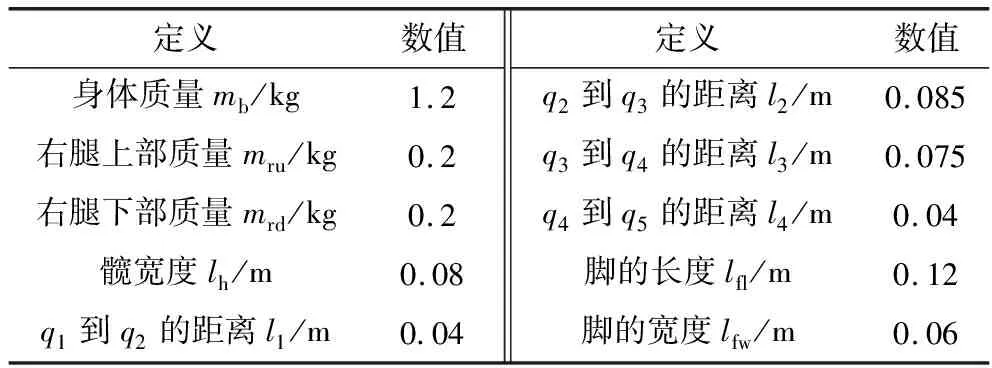
表1 双足机器人的基本参数

图1 实验机器人的连杆结构
拟议的双足机器人步态行走基于以下假设。
1)上身在任何时候都保持直立的姿态。人的躯干俯仰角度一般在3°以内[18],多数相关研究表明,这个假设是可以接受的[8-10,12-16]。
2)双脚总是与地面平行。常见的多数仿人机器人没有脚趾,在抬脚和落脚时,不能发挥改善驱动性能的作用[19]。

1.2 ZMP方程
在诸多双足机器人的动态稳定性指标中,使用最为广泛的是零力矩点(zero moment point,ZMP)概念,ZMP是地面上由重力和惯性产生的总力矩水平分量为零的点[20]。设双足机器人的5个质量点分别为身体b,左腿lu,左足ld,右腿ru,右足rd,组成集合Pc={b,lu,ld,ru,rd},位置为{ri|i∈Pc},其中b与髋中心点的距离为hb。同时,设左髋关节lh,左膝关节lk,左踝关节lf,右髋关节rh,右膝关节rk,右踝关节rf,组成集合Pr={lh,lk,lf,rh,rk,rf},位置为{rj|j∈Pr}。机器人的位置示意如图2所示。

图2 双足机器人的五质心模型
在ZMP位置rZMP=[xZMP,yZMP,0]T处,地面作用力的合力F产生的力矩MZMP,与由于各质心的重力和惯性施加于机器人身体的合力矩M,满足
n×MZMP=n×(M-rZMP×F)=0
(1)
式中
(2)
(3)

(4)
1.3 有效ZMP区域
双足机器人的建模中不可避免的存在建模误差,HONG等将ZMP固定在支撑脚的中心,以实现最稳定的行走[12],但这并不是高效的方法。在支撑脚的区域内,划出一些边缘区域,用来补偿建模误差[16],并使ZMP位于支撑脚中部的有效ZMP区域(allowable ZMP region,AZR)方法,是一种在克服误差与高效行走之间权衡的较好方法。设足长lfl、足宽lfw的双足机器人,步行时步幅为s,双足Y轴距离是w,AZR示意如图3所示。文中分别用ηl=lal/lfl和ηw=law/lfw表示脚长方向和脚宽方向的容限,后续步态规划算法中,ηl取固定值,并约定η=ηw。以左脚在前,右脚在后为例,在第1个DSP中,AZR是由点r1,r2,r3,r4,r5,r6构成的六边形区域;在SSP时,AZR是由点r4,r5,r6,r7构成的长方形;在第2个DSP中,AZR是由点r5,r6,r7,r8,r9,r10构成的六边形。
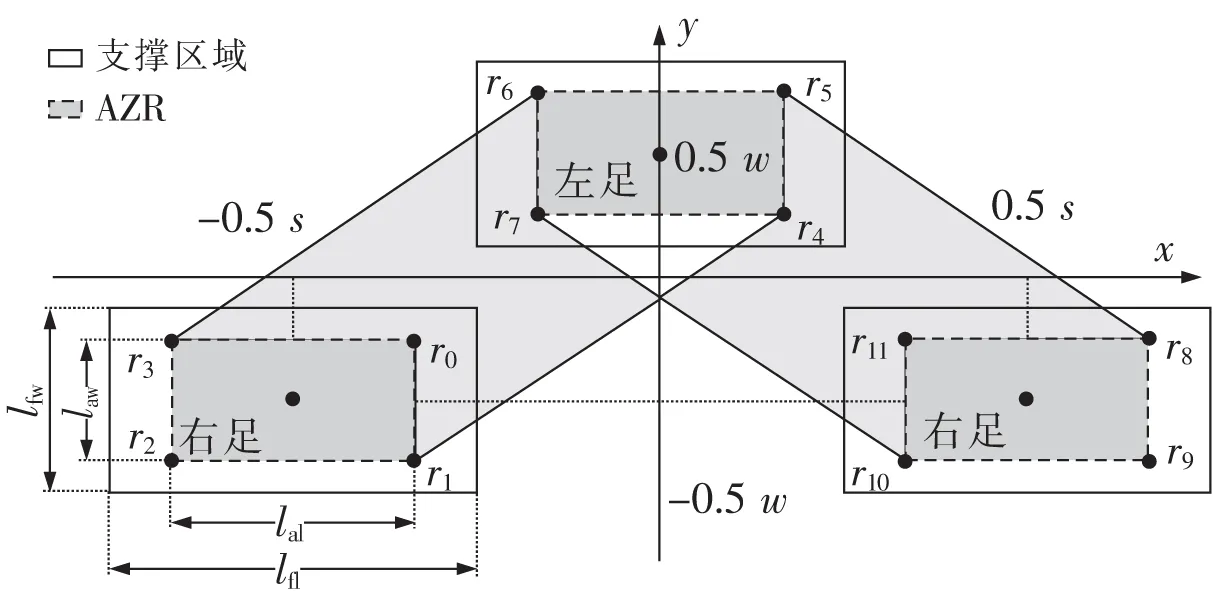
图3 双足机器人的AZR
1.4 能耗指标函数
依赖电池提供能源的双足机器人,能耗E包括运动能耗Em和非运动能耗Ea这2部分[22]。Em用于维持电机的运行,是系统能耗的主要部分,其值为电机瞬时电压向量um(t)和电流向量im(t)对时间t的积分。Ea用于传感器、控制器和内部电路运行,其功率Pa在一段时间内是相对稳定的,可以表示为时间t的线性函数。即
(5)

(6)
1.5 问题定义
基于前面的分析,文中的节能步态规划问题可表述为
1)给定双足机器人步长和AZR,允许身体在行走中三维运动,满足1.1中假设条件,确定最小化能耗指标函数E的步态轨迹。
2)已知运动距离,确定包含开始步、中间步和停止步的完整步态轨迹,并利用AZR,提高双足机器人行走的鲁棒性。
2 步态规划算法
2.1 算法概述
文中提出的步态规划算法分为步态参数优化(gait parameter optimization,GPO)算法和步态合成(gait synthesis,GSYN)算法2部分,如图4所示。
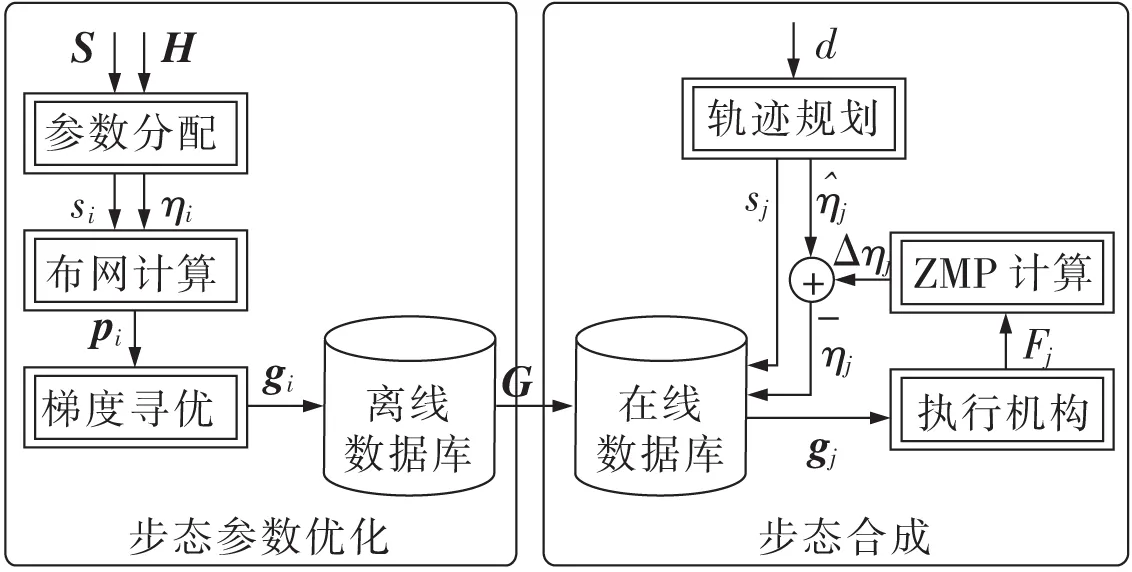
图4 步态规划算法示意
1)GPO算法从步长集合S和AZR容限集合H选取元素si和ηi,在si傅里叶级数表示空间中布网运算,获得符合ηi要求的种子集合Pi,在Pi中元素pi的邻域,依据文中1.4中的算法计算能耗指标函数,按照最优梯度法迭代运算,获得最小能耗指标函数的电机优化角度序列(步态轨迹)gi={qi(n)|N=1,2,…,N},存入数据库。
GPO算法运算时间较长,算法宜于离线运行,对S和H完成运算后,将离线数据库中的结果,复制到在线数据库,GSYN计算中可实时调用。

2.2 GPO算法
GPO算法用于生成步态控制的电机角度序列,是文中算法的核心。按照双足机器人行走的精度要求,从最小步长至最大步长离散取值,确定S中的元素si。H从值域[0,1]选取若干等级,对应不同的鲁棒性要求的ηi。GPO算法从S和H依次选取元素si和ηi,进行布网梯度优化计算,以获得满足最小化E的gi。
2.2.1 布网计算方法
所谓布网计算,是将多维参数取值按照一定间隙离散化为网格,使构成的参数空间网格化,进而计算各个网格交点函数值的过程。若机器人步长为si,身体b进行满足1.1中假设1的三维周期运动,位置rb(n)=[xb(n)yb(n)zb(n)]T可用有限阶的傅里叶级数表示,即
(7)
式中rb(n)用参数{ak|k=1,2,…,18}表示;N为步态周期,ω0=2π/N。若ak∈[dk,uk]按照间隙μk取值为Ak={dk,dk+μk,dk+2μk,…,uk},k=1,2,…,18。则布网形成的交点集合U为(Ak|K=1,2,…,18)的笛卡尔积,即U=A1×A2×…×A18。
另一方面,若设机器人运动起始为左腿在前,右腿在后的双支撑阶段,随后右腿摆动向前,且右脚rf起始位置为[0 0 0]T,并设运动满足1.1中假设3,则位置rrf(n)=[xrf(n)yrf(n)zrf(n)]T运动轨迹为
(8)
式中w为步宽,cm;hf为步高,cm;N1=N/16,N2=7N/16,N3=3N/8。机器人的双足运动具有对称性,左脚轨迹rlf(n)为rrf(n)时移N/2,并在Y方向对称取值。
HERZOG等论述了已知rb(n)和rrf(n)求解双足机器人关节角度q(n)的逆动力学方法[24]。布网空间U一般具有较大的元素数目,考虑rb(n)具有的运动特性,可排除rb(n)在U中的一些不合理取值,从而减少需要的逆动力学计算数量。常见的rb(n)特性有如下特点。
1)xb(n)在步态周期内单调增。
2)yb(n)前半个周期为凸函数,后半个周期为凹函数,且在半个周期内无拐点。
3)zb(n)在前、后半个周期内均为先单调增,后单调减。
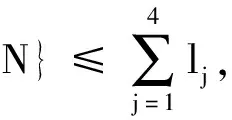

2.2.2 梯度寻优算法
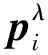

算法2.1 梯度寻优算法
给定Pi,δλ,AZR,
forλ=1,2,…,Λ do

重复进行


end for
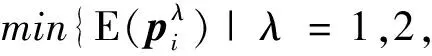
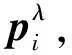
2.3 GSYN算法
给定运动距离d,规划S*={sj|j=1,2,…,c}包括2个起始步s1和s2,2个停止步sc-2和sc-1,多个循环步sm,m=3,4,…,c-3。其中s1=sc-1,s2=sc-2,循环步sm具有相等的距离。起始步和停止步的总长db控制在1~2sm,即sm (9) yMIN=min{c0(yZMP(n)-yAZR(n))|n=1,2,…,N} (10) 按照增量PI控制算法,可计算Δηj (11) 式中kP,kI分别为比例、积分系数。 (12) 表2 梯度寻优中的 图5 能耗指标函数收敛曲线 为对比算法性能,以机器人髋高度固定[15]和髋高度按余弦波形垂直变化[16],其他条件与文中算法相同,设置算法二和算法三,经过优化计算后,其E分别为280.4和252.4 mJ,并标识于图5中。设机器人步态以DSP起始,单步周期N=16,DSP比率σ=0.25,3种算法的单步ZMP轨迹如图6所示,其中文中算法采用能耗E=231.5 mJ时的步态数据。 图6 ZMP数据分析 表3 ZMP轨迹分析 若取d=90 cm,sm=12 cm,按照式(9)计算得c=10,s1=2 cm,s2=7 cm,则机器人运动的步长S*={2,7,12,12,12,12,12,12,7,2}。在机器人运动的每步均以ηj=5/6从在线数据库中取得gj=[q1q2…q16],j=1,2,…,10,控制机器人的关节运动,对应的双足机器人步态运动的动态仿真如图7所示。 图7 机器人步行的动态仿真 依照前述仿真数据,实测机器人行走试验如图8所示。试验中,设定行走距离90 cm,在第1步为右脚支撑,设定SSP右脚yAZR=-1.5 cm,初始η1=1/3,在行走中,检测到yMIN=1.53 cm,经过式(11)PI及逻辑运算,得Δη1=-1/3,按式(12)取η2=2/3。其后,经过第2,3步的校正后,η值稳定在5/6。若控制中选用η1=1/3的控制方法,行走sm=12 cm时,E=276.3 mJ。而采用文中的GSYN算法,调整η=5/6后,行走12 cm的E=231.5 mJ,其值下降了16.21%。 图8 机器人行走的试验 1)电机驱动的机器人具有质量分散的特点,建立多质心机器人模型可较好的描述机器人物理特性。在机器人多质心模型的基础上,建立了以负荷转矩为主要参数的能耗函数,能在仿真中精确而方便地计算机器人运动的能耗指标。 2)GPO算法中的对运动空间网格化的过程中,要求单个网孔内不出现多个峰值,选择合适的网孔间隙,此方法适用于多数系统的优化。算法的梯度逼近中按照精度要求,确定逐次逼近的步长,在网孔规模较大时,可采用将网孔空间再次网格化的方法加速逼近过程。GPO算法对系统优化的过程中需要进行大量的运算,可在有限的时间内确定找到最优值,随着计算机科学的进步,其对比随机优化算法,将愈加表现出其优越的性能。 3)GSYN算法按照实际机器人行走的要求,规划含起始步、中间步和停止步的完整运动过程。在机器人的行走过程中,算法根据反馈的ZMP数据,修改机器人运动的AZR,从而克服建模和环境误差的干扰,可实现低能耗和高鲁棒性的折中,较好地解决具有高度非线性特征的双足机器人行走问题。因此,该算法也作为一种新途径,推广到煤矿救援机器人的开发中。
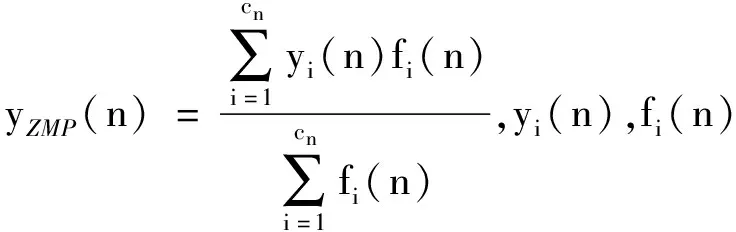

3 仿真与实验分析





4 结 论
