基于广义帕累托分布的中纬度地区地磁场极值预测

2021-06-17周宁馨查虹丽马龙雄

西安科技大学学报 2021年3期

周宁馨，刘青，查虹丽，马龙雄

(西安科技大学电气与控制工程学院，陕西西安 710054)

0 引言

极端地磁暴是一种客观存在的自然灾害。磁暴期间的感应地电场在电网中诱发的地磁感应电流(GIC)，对电网的威胁已引起普遍关注[1-3]。

目前国内关于感应地电场和地磁感应电流的计算多采用固定的地磁场变化率，或者针对某一次特定的地磁暴事件进行评估分析[4-7]。实际上，自然灾害对实际工程造成的潜在风险进行评估时，需要考虑的并非已经观测到的一般事件的概率，而是极端事件可能发生的微小概率，因此往往采用百年重现水平值作为评估的输入条件[8-9]。

BEGGAN等人将地磁场极值估计的结果与英国大地模型和高压输电网络相结合，预测了100 a一遇和200 a一遇的极端地磁暴场景产生的变压器节点GIC[10]。这项研究采用的极值数据来源于THOMSON等人对欧洲地磁场重现水平的估计，他们利用极值理论建立地磁场水平分量的分钟值及其变化率的广义帕累托分布(generalized pareto distribution，GPD)模型，得到高纬度地区100 a一遇和200 a一遇地磁场可能出现的极值范围[11]。

地磁暴作为一种全球性、几乎同时发生变化的地磁场扰动，从赤道到极区均可观测到显著变化现象[12]。但不同纬度地区地磁场所受到磁暴影响的机理有所差异[13-15]，因此需要结合中国高压输电网络主要处于中纬度范围的地理特点，选取中纬度地区的地磁台观测数据进行分析。

国内利用极值理论对极端天气进行重现水平的分析应用广泛，但在地磁暴领域的研究目前相对较少，吴伟丽等人利用磁场数据和复镜像法构造地电场统计样本，通过建立地电场的GPD模型估算出喀什地区50 a一遇和100 a一遇的感应地电场强度[16]。

文中以兰州地磁台的观测数据为基础，利用基于广义帕累托分布的超阈值模型(peak over threshold，POT)对地磁场的水平分量及其分钟变化率进行拟合，通过极大似然估计方法和轮廓似然函数得到T年一遇的重现值结果，为施加地磁场激励的幅值选取提供理论参考。

1 地磁暴诱发的感应地电场

现有地磁暴感应地电场计算方法中应用最广泛的为平面波理论，即假设空间电流源为电流密度恒定，距离地面足够远的无限大面电流。若大地电导率均匀，则根据麦克斯韦方程和法拉第电磁感应定律，通过地磁台观测的地磁场水平分量估算出感应地电场为

(1)

(2)

式中Ex，Ey分别为南北及东西向感应地电场；μ0为真空磁导率；σ为大地电导率；gx(u)为南北方向磁场变化率；gy(u)为东西方向磁场变化率。

由于地磁台数据为离散序列，在编程计算时需要将公式离散化。设地磁台记录水平分量B数据的采样周期表示为Δ=Tn-Tn-1，在采样间隔[Tn-1,Tn]内有g(t)=(Bn-Bn-1)/Δ。设t=TN，代入式(1)并进行离散化处理得

(3)

将g(t)=(Bn-Bn-1)/Δ代入上式得

E(TN)=

(4)

其中bn=Bn-Bn-1为地磁场分量的一阶差分。通过式(4)可以看出影响磁暴感应地电场的关键因素是地磁场水平分量变化率。

以2006年12月的地磁暴事件为例，基于兰州地磁台(LZH)磁暴监测数据计算感应地电场。图1给出了磁暴期间Bx和dBx/dt随时间的变化曲线。设置均匀大地电导率为0.001 S/m，由此计算的东西方向感应地电场Ey如图2所示。

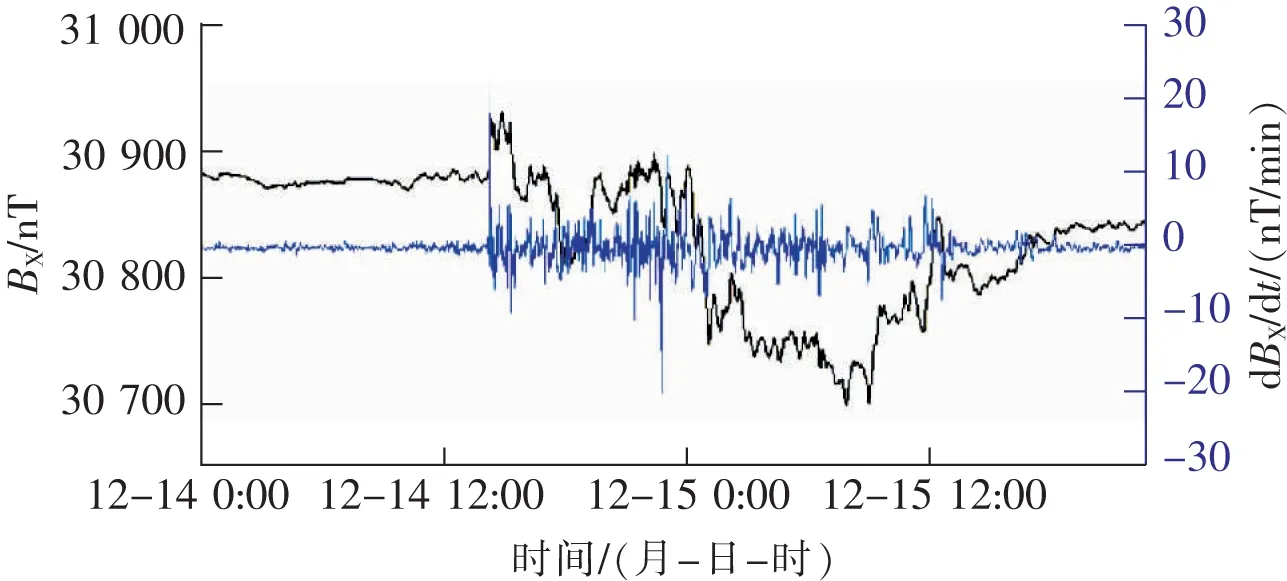
图1 磁暴期间地磁场水平分量及其变化率

图2 磁暴期间感应地电场

对比可知，相比较于地磁场分量Bx，地电场幅值出现最大值的时刻与地磁场变化率dBx/dt更相关，证明地磁场变化率是地磁活动影响电力系统过程中最主要的物理量，故文中选取地磁场水平分量BH和变化率dBH/dt进行概率模型的拟合。

2 地磁场的极值预测模型

2.1 极值理论与应用

鉴于地磁场的观测数据有独立的分钟值样本，文献[8]提出在地磁活动的统计分析中广义帕累托分布(GPD)最为适合。这种基于广义帕累托分布对超过某一充分大的阈值的所有观测数据进行拟合的模型称为超阈值(POT)模型。

假定地磁场水平分量及水平分量变化率的随机变量列x1，x2，…，xn服从GPD分布，其表达式为

(5)

式中μ为位置参数；σ为尺度参数(σ>0)；ξ为形状参数。位置参数μ将选定为阈值u。随机变量列x1，x2，…，xn是否服从GPD分布还需要进行模型检验。

通过将地磁台的观测数据集与GPD函数进行拟合建立POT模型，可以评估观测数据集以外更为极端的地磁活动发生概率[17]。通常采用极大似然估计法确定模型中的参数，也可利用轮廓似然函数得到更为精确参数的估计范围[18]。

在对参数进行估计后，通过概率分布函数中分位数p的定义，可以得到某一确定重现期T下磁暴极值的估算公式

(6)

式中N/Nμ为样本总数与样本中超出量个数之比；xp为重现期为T=1/(1-p)所对应重现水平。

利用P-P图(概率图)与Q-Q图(分位数图)进行模型检验，理论上当某种分布函数与样本实际分布越贴近时，P-P图和Q-Q图应该更近似为直线[19]。通过分析模型检验结果可以确定选取的概率分布函数是否符合实际数据的真实分布情况。

2.2 地磁数据资料

选取我国观测状态正常、保存数据记录年份较长的兰州地磁台(LZH)进行分析[20-23]。结合我国超、特高压输电网络主要处于中纬度范围的地理特点，同样选取国际上其他4个中纬地磁台数据进行GPD拟合，并将重现值估计结果对比分析。地磁台地理坐标和数据记录时间见表1。

表1 台站列表

2.3 模型拟合与检验

利用R语言进行数据处理，建立LZH地磁台2001—2019年的地磁场水平分量分钟值BH的POT模型。拟合过程中需要选取某一确定阈值，阈值太大将只有少数几个超出量，导致估计量方差过大；而阈值太小则使得超出量与GPD分布出现较大偏差，估计量成为有偏估计[24]。

图3给出了形状参数和修正尺度参数随阈值变化的趋势，修正尺度参数σ*=σ-ξμ。若阈值适当，则超出量服从GPD分布，参数的估计值应该保持在变化较小的范围内。从图3可以看出在[31 050，31 055]的区间内，ξ和σ*的估计量都比较稳定。为了保证模型的准确性，应在参数估计量呈平稳趋势的区间内尽量选取较大的阈值，因此选择μ=31 055，此时阈值门槛的筛选比例为99.97%，与文献[8]中确定的筛选标准相近，同时超阈值的样本量不足1%，可以较好的满足GPD尾部建模条件。

通过求解GPD分布的对数似然函数的最大值，得到尺寸参数σ极大似然估计为9.295 6，标准误差1.239 0；形状参数ξ极大似然估计为-0.291 9，标准误差0.085 8。由估计值和标准误差可知σ和ξ置信度近似为95%的置信区间分别为[6.87，11.72]和[-0.46，-0.12]。由于形状参数ξ决定分布的类型，图4利用ξ的轮廓对数似然函数得到更高精度的95%置信区间为[-0.44，-0.09]，与之前得到的区间相比范围稍有缩小。ξ所在置信区间为负意味着对应一个有界分布，这与地磁场水平分量具有上限的实际观测情况相符合。

图4 形状参数ξ的轮廓似然估计

图5为利用GPD分布拟合地磁场水平分量的POT模型诊断图。图5(a)和图5(b)分别为P-P图和Q-Q图，可以明显看出样本数据点均落在一条直线。图5(c)为重现水平估计值随着重现期变化的趋势及其95%置信区间，由于ξ的估计值和考虑置信区间后均为负值，相应分布具有有限上界，故重现水平渐进地趋于某个有限值。最后，图5(d)的概率密度曲线也与样本数据直方图相吻合。诊断图表明POT模型适用于地磁数据的拟合，而且在进行模型数值外推时具有稳定表现。

图5 地磁场水平分量BH的POT模型拟合诊断

在分析地磁场水平分量变化率时同样利用式(5)拟合建立POT模型，数据来源于BH进行差分处理后的分钟值变化率dBH/dt。结合MRL曲线和参数随阈值变化情况，选取的阈值门槛为99.5%。对GPD分布中参数进行估计，得到尺寸参数σ极大似然估计为6.311 6，标准误差2.350 3；形状参数ξ极大似然估计为0.071 4，标准误差0.305 7。通过计算得到形状参数ξ的95%置信区间为[-0.53，0.67]，利用轮廓似然曲线得到更精确的置信区间为[-0.28，0.64]。

拟合诊断图如图6所示。图6(a)和图6(b)分别为P-P图和Q-Q图，可以看出样本点几乎均匀地落在参考直线附近，表明POT模型适用于对样本数据的拟合。图6(c)的重现水平曲线近似为线性，考虑到ξ的估计值和大部分置信区间都为正，相应分布的没有上界，这表明极端地磁活动不被某些最大值所限制；同时服从Gumbel或Fraechet尾部分布，意味着其概率将随着重现水平的增大而呈指数或多项式下降趋势，在更长的重现期才可能会出现更高的极值。图6(d)的概率密度曲线与样本实际分布的直方图较为吻合，综合4个诊断图认为POT模型同样适用于对地磁场水平分量分钟值变化率dBH/dt的拟合。

图6 地磁场水平分量变化率dBH/dt的POT模型拟合诊断

3 重现水平估计

在建立地磁场水平分量BH和地磁场水平分量变化率dBH/dt的POT模型后，根据式(6)计算出不同重现期下的轮廓对数似然曲线，如图7和图8所示，包括50 a一遇、100 a一遇和200 a一遇极值的重现水平估计。图中横坐标为重现水平范围，纵坐标为轮廓对数似然函数，其极大值对应横坐标即为重现水平估计值，用于参考的水平直线指出了该重现水平的95%置信区间。

图7 地磁场水平分量BH重现水平的轮廓似然估计

图8 地磁场变化率dBH/dt重现水平的轮廓似然估计

可以看出随着重现期的增加，地磁场水平分量BH和地磁场水平分量变化率dBH/dt的轮廓对数似然曲线均表现出更强的不对称性。由于重现期越长，观测数据所能提供的信息就越少，得到重现水平估计值的95%置信区间就越宽。

表2给出在不同重现期下，地磁场水平分量分钟变化率dBH/dt的估计上限和以最大观测值为基准的放大倍数，表中第1行为20 a观测数据中的最大值。可以看出随着重现期的增长，dBH/dt呈现出较为缓和的增长趋势，而非简单的线性关系。相比较于采用统一倍数标准对观测历史最大值进行放大[2]，POT模型可以为极端磁暴活动提供更为准确的预测极值参考。

表2 T年重现期的dBH/dt重现水平上限值

考虑到经纬度的差异，利用GPD分布对全球范围内中纬度地区的5个地磁站台观测数据进行拟合，给出了最大观测值与所建立的POT模型中100 a一遇和200 a一遇估计结果的对比。图9和图10分别为5个不同站台的地磁场水平分量BH和地磁场水平分量变化率dBH/dt的极端磁暴场景估计值，括号内为站台所在纬度。

图9 中纬度地区地磁场水平分量BH估计值

图10 中纬度地区地磁场水平分量变化率dBH/dt估计值

从图10中可以看出，随着重现期的增加，地磁场变化率dBH/dt的重现水平有较大幅度的增加。此外，纬度相近的地磁站台SPT与SUA的BH和dBH/dt重现水平均有较大差异，表明dBH/dt不仅与所处纬度有关。综合全球范围中纬度各个地磁台的极值预测情况，给出中纬度地区100 a一遇的磁暴期间地磁场分钟变化率约为200～500 nT/min，200 a一遇的磁暴期间地磁场分钟变化率约为200～800 nT/min。