周期荷载激励下覆冰输电线的舞动特征研究

杨曙光,刘小会1,,梁浩博,蔡萌琦

(1.重庆交通大学 省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074；2.重庆交通大学 土木工程学院，重庆 400074；3.成都大学 建筑与土木工程学院，成都610106)

在如今这个信息化的时代里，电能早已成为了人们日常生活中不可或缺的一部分，因此输电线路的安全稳定运行就十分重要。在恶劣的自然环境中，雨雪冰冻天气容易使得输电线覆冰，覆冰输电线在外部风的激励下又容易产生单个或多个半波大振幅、低频率的舞动[1]。输电线舞动又会产生跳闸、断股、输电塔倒塌等事故。为了使电力能源远距离安全、稳定地传输，输电线路的非线性舞动特征研究是十分有必要的。

早在1932年国外学者Den Hartog[2]就提出了垂直舞动机理，研究发现覆冰输电导线舞动横向幅值远小于竖向幅值，表明舞动主要发生在竖直方向，并在同年提出了邓哈托判别准则。Desai等[3]在邓哈托判别准则的基础上，运用有限元方法研究相邻跨会对舞动幅值产生的影响；在此基础上，Rega等[4]运用摄动法求解了弱激励下的非线性偏微分方程，分析了幅频函数图像的多值性，然而以上论文均没有考虑空气动力荷载。此外，1983年，Luongo等[5]考虑弹性电缆的非线性运动学关系推导出了连续非线性方程，并研究了输电线舞动风速和相应参数的关系及其气动稳定性；曹化锦等[6]运用ANSYS建立了输电塔及输电线的有限元模型，对不同风况的输电塔和输电线耦合体系进行了舞动仿真，得到了舞动振幅和输电塔的动力响应；张栋梁等[7]采用Hamilton原理建立了4自由度非线性舞动方程，提出了一种新的覆冰输电线舞动分析的有限元模型。然而以上论文没有考虑相邻档导线之间的影响。王建军等[8]用数值方法研究了单自由度参数振动系统在外荷载激励下多频响应的非线性特征；黄坤等[9]研究了梁索耦合结构在高频激励、低频激励和高频与低频组合激励下幅值随激励参数变化的规律；赵跃宇等[10]对参数激励下斜拉索主参数共振的稳定性分析表明固有频率和外激励参数对斜拉索稳态解和稳定性存在直接影响。然而以上论文对于索的研究没有考虑气动荷载对输电线的负阻尼影响。郝淑英等[11]建立四分裂覆冰输电线周期振动的非线性动力学偏微分方程，揭示了输电线在舞动过程中会出现固有频率漂移的现象；刘海英等[12]建立了覆冰四分裂导线连续体非线性动力学模型，运用数值模拟和理论分析发现非线性因素会使得振幅对频率产生影响。然而以上论文研究了输电线在气动荷载的舞动特征，并未同时考虑周期激励和气动荷载对输电线的影响。

长期以来，科研工作者对输电线舞动做了深入的研究，然而对于考虑动态风对覆冰输电线的作用和考虑相邻档对舞动档的影响是比较少的。本文考虑覆冰输电线由于受到动态风与相邻档的影响存在周期激励的一般性，将施加有空气动力荷载和周期激励的覆冰输电线作为研究对象，运用多尺度法求出该系统的解析解；对解析解和数值解进行精确度比较，并且分析风速、张力、弹性模量的变化对覆冰输电线幅频曲线的影响。

1 输电线舞动力学模型

对于平原地区的覆冰输电线，大部分档的导线可视为等高差输电线，因此本文选取两端固定支座的等高差单档输电线作为研究对象。通常风都是不稳定的，本文在静态风的基础上添加周期激励，将覆冰输电线看作受到一个有动态影响的风荷载；并且选取最危险工况认为风沿水平方向且与导线的轴向垂直，所建立的单档导线舞动的力学模型如图1所示。(x，y)为平面直角坐标系，s表示曲线的自然坐标。覆冰输电线档距为L，其变形可分为两个阶段进行描述：(1)仅在重力作用下的静止状态时，平衡状态的构形为ξ1，垂度为d。(2)输电线覆冰后，在风的激励下，输电线在O-xy平面发生竖向振动，由初始构形ξ1经过一段时间后变化为ξ2（仅考虑竖直向振动）；由此竖向振动所引起的x、y方向上的动位移可分别表示为函数u(s，t)，v(s，t)，p*cos(Ωt)为自激-受迫系统中的受迫激励项，将受迫项中的激励幅值p*考虑成施加在覆冰输电线竖直方向的均布荷载，并且本文取图1中微段ds作为输电线在静止状态下的研究对象。

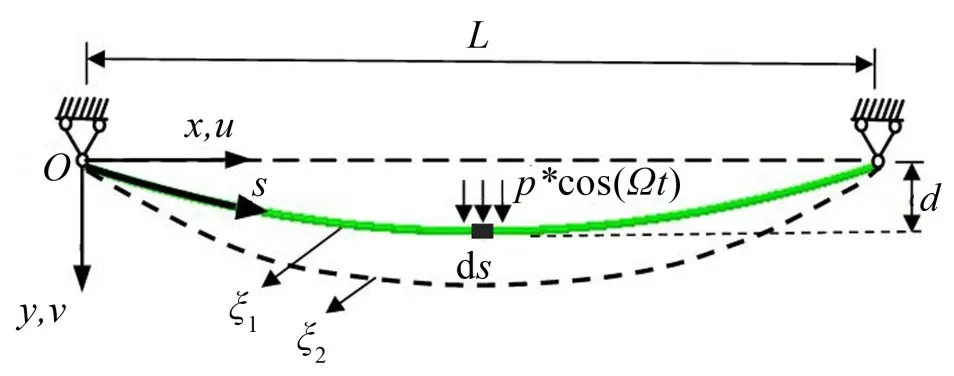
图1 输电线平面图

如图2所示，输电线覆冰后，其横截面形状从原有的圆形变成了新月形。选取图1中覆冰导线微段ds的横断面作为研究对象，以未产生振动时微段的质心平衡位置作为参考坐标系O1-zy，且振动中心为O1；其中O1z为水平轴，p*cos(Ωt)为受迫激励项。平均风U作用在覆冰输电线上会产生向上的升力Fy=ρU2hCy/2，竖直向的空气动力系数可拟合为Cy=A′α+B′α3，其中代表运动状态变化的攻角α=/U，表示水平风作用于覆冰输电线产生的竖直向振动速度，并且A′和B′表示竖直向空气动力拟合系数，则升力Fy[13]：

图2 输电导线横截面图

式中参数分别为

式中：ρ表示空气密度，h表示输电线的直径。

输电线属于大跨度的柔性索结构，针对这种类型的结构，可做出如下假设：

(1)在静止状态下，输电线的重力平衡曲线可以通过抛物线y=4d[x/l-(x/l)2]来描述。

(2)假设H为导线静态下初始张力的水平分量。

对于研究的小弧垂输电线，结合图1只考虑静态风作用下输电线竖直方向运动的控制方程为[4]

式中：E表示输电线的弹性模量，S表示输电线的横截面积，m表示单位长度的质量，μ表示结构阻尼，y′表示抛物线方程对x的一次导数，v′表示竖直方向运动函数对x的一次偏导，表示竖直方向运动函数对时间t的一次导数，表示竖直方向运动函数对时间t的二次导数。

输电线在自然环境下，受到自然风作用下也会产生舞动。式(3)模型的建立主要是针对静态风U，而自然风可以表示成平均风U和脉动风(t)的叠加。在工程分析中，可以采用谐波叠加法进行脉动风荷载模拟，利用谱分解和三角级数叠加来模拟脉动风的随机过程，将随机信号通过傅里叶分析变换得到一系列不同频率和幅值的正弦波或其他谐波[14]，即可以表示出自然风对覆冰输电线的气动力表达式：

式中：Ui为每个谐波成分对应的幅值，Ωi和φi为脉动风变换后对应谐波项的圆频率和相位差，并且忽略了气动力的高阶小量。自然风中稳定的部分使得输电线产生自激振动，不稳定的部分会引起外部激励[15]。自然风对输电线的气动力如式(4)所示。其中存在谐波激励项，因此可以在传统稳定风作用下的输电线舞动方程基础上添加周期激励来模拟动态气动荷载对输电线的作用。此外，如果考虑相邻档导线的影响，则相邻档导线也会给舞动档导线施加一个周期激励，如图3所示。

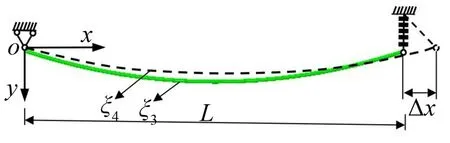
图3 输电线平面图

图3中Δx是相邻导线运动导致的端部位移，ξ3原始导线的构型，ξ4为运动后导线的构型。忽略输电线横向变形及几何非线性引起的附加弹性动张力，可以容易给出上述导线的运动控制方程：

式中：8dESΔx·cos(Ωt)/(L2LS)表示端部周期位移的激励项，该端部位移是相邻档导线舞动所产生的[16]，其中Ω为端部位移激励的圆频率，Ls=L[1+8(d/L)2]为考虑垂度的输电线长度。

自然风对输电线的作用，自然风中的平均风使得覆冰输电线发生自激振动，脉动风使得覆冰输电线发生受迫振动；结合脉动风与相邻档对舞动档的影响来考虑，将原有空气动力荷载和周期激励组合来进行模拟。在本文中为了使公式具有一般意义，主要研究外部激励的参数变化对舞动特征的影响。那么对式(3)添加如图2中的简谐激励p*cos(Ωt)后得到自激-受迫系统的控制方程：

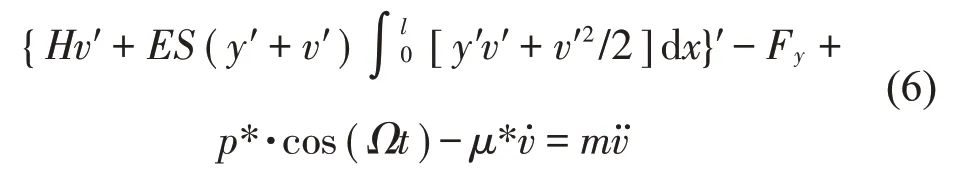
采用模态叠加法将v(x,t)表示为模态函数f(x)和时间函数q(t)的乘积：

将式(7)代入式(6)后可得到一个非线性常微分方程，则竖直向运动函数对x和时间的导数分别为，其中模态函数为f(x)=sin(nπx/L)，令n=1，即以研究1阶阵型为主。为了使方程便于计算，采用Galerkin方法将方程化简得到覆冰导线舞动的振动动力学方程：

式中的参数分别为

对于式(9)，参数w为输电线系统的固有频率；由于p*考虑成竖直方向的均布荷载，因此受迫项的模态函数f1(x)=1，I的值取决于模态函数f(x)，其定义如下：

在式(8)中，针对弱非线性系统，对振幅进行限制，可以对阻尼项和非线性项作如下转换：

式中：ε是与时间有关的小量为系统新变量，为了公式简洁，后文仍用q、μ、来表示。将式(11)代入式(8)中可得弱激励下接近共振的自激系统：

2 非线性舞动方程解析解求解

2.1 弱激励下的自激系统

对于弱非线性系统式(12)，即为接近共振的受迫振动，取ε=0.1，偏微分算子符号、受迫项频率以及振幅可以划分为

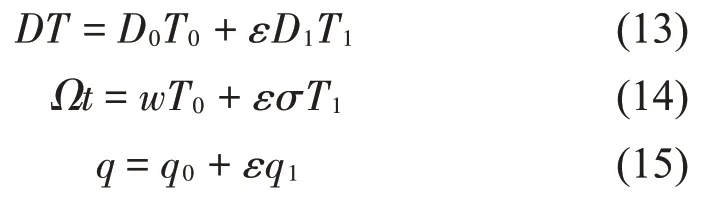
式中：σ为激励频率的调谐参数，将式(13)、式(14)和式(15)代入式(12)后，比较ε同次幂系数后得到一组关于εn(n=0，1)线性偏微分方程：

式中：Dk表示对Tk求偏导数，求解式(16)得到：

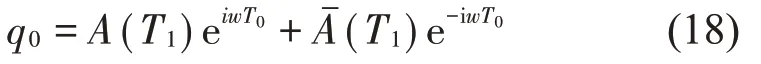
式中：A可定义为

将式(18)和式(19)代入式(17)，分离久期项得到对应的1阶微分算子，然后再分离微分算子的实部和虚部可得到系统振幅和相位的变化率方程：

为了确定稳态运动定常解的振幅和相位，引入γ=σT1-β,令D1A=0，然后消掉γ得到幅频响应方程：

2.2 强激励下的自激系统

将式(12)改写为远离共振的受迫振动，则舞动方程为

将式(13)、式(14)和式(15)代入式(23)，其中式(23)Ωt=ξT0+εσT1，然后按照相应小量阶次进行划分可得到一组关于εn(n=0,1)线性偏微分方程：

式中：Dk表示对Tk求偏导数，式(24)的解为

式(26)中A和B可分别表示为

将式(26)代入式(25)得到：

限于文章篇幅，对于式(29)，先不考虑谐波共振，因此为了防止产生超谐波和次谐波共振项，取Ω=w/4。结合式(27)、式(28)和式(29)分离久期项得到对应的1阶微分算子，然后再分离微分算子的实部和虚部可得到系统振幅和相位的变化率方程：

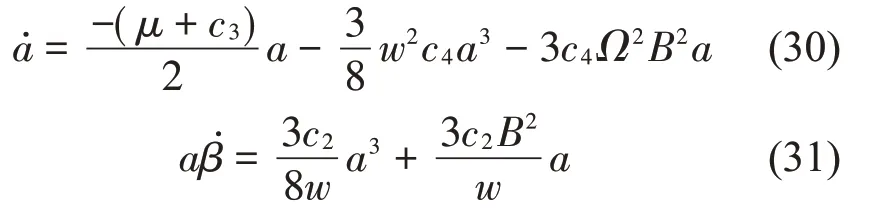
对式(31)进行时间积分后可得到：

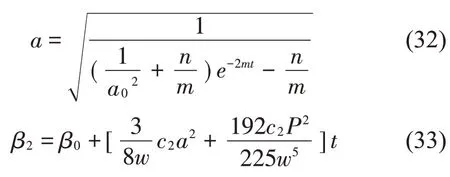
对于幅值函数a(t)的表达式，其中m和n取决于输电线的物理结构参数和气动参数，并且m决定了振幅的变化趋势。

当外激励比较弱时，自激-受迫系统中存在有自激振动，即满足存在自激振动的充分必要条件为

此时满足参数m＞0，那么式(32)即为收敛的情况，激励幅值满足式(34)的条件，此时系统仍然可以形成自激振动，不会破坏自激振动的条件，系统的稳态运动就由自激振动和受迫振动叠加而成。

当外激励比较强时，m＜0，即破坏自激振动的条件为

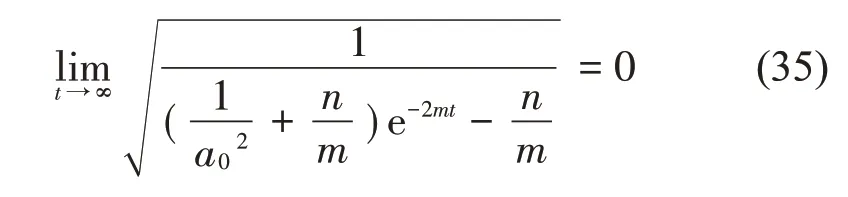
激励幅值不满足式(34)的条件，那么自激振动振动幅值随着时间变化趋近于0，激励幅值符合式(35)的条件，则无法形成自激振动，表明此时自激-受迫系统中不存在自激振动。式(32)、式(34)和式(35)中各参数分别为

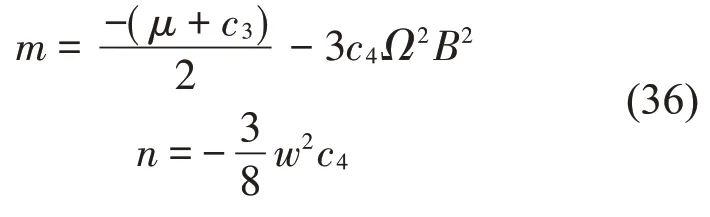
3 数值解与解析解分析

输电线覆冰后，冰型对气动力也存在很大的影响，因此选用具有代表性的新月形作为研究对象。为了便于分析比较，选用文献[17]的几何参数、材料参数和相应的气动力参数如表1所示。

空气动力荷载作用下的覆冰输电线，经过物理建模和数学分析得到运动状态下的偏微分控制方程，运用模态叠加法和Galerkin法得到舞动常微分方程式(8)。如图4所示。使用表1的数据并且给输电线施加竖向的初始扰动后，令初值竖向扰动q(0)=0.01 m，并且将激励幅值p*=0.186 8 N/m代入式(8)中，计算的步长取1/10，用MATLAB求解式(8)得到覆冰输电线舞动时中点的竖向位移时程图像。在1 725 s后振动幅值趋于稳定；局部放大图为幅值稳定后2 000 s～2 020 s的时程位移曲线。从图4中可以看出，施加受迫激励幅值稳定后的时程位移图，其幅值随时间变化会产生向上或者向下不规则的抖动，主要是由于周期激励项的频率与系统固有频率不一致而造成的。

表1 覆冰输电线线路物理参数

图4 位移时程图

在自激-受迫振动系统中，既存在平均风的气动荷载激励，又存在脉动风与相邻档影响的周期激励。图5是使用Maple软件绘制自激-受迫系统的振幅解析解式(32)得到的，其中曲线b、c、d、e分别对应激励幅值p*=0.934、3.736、9.343、14.948 N/m中自激振动的幅值变化；激励幅值增大，使得空气动力荷载下覆冰输电线的自激振动的幅值越来越小；随着激励幅值的增大，自激振动幅值曲线达到稳定的时间也不断延长；图5中曲线b、c、d即在判别式(34)的范围内，曲线e在判别式(34)的范围外，随着激励幅值p*=0.934 N/m对应的曲线b增加到p*=9.343 N/m对应的曲线d，响应幅值从点ab下降到点ad；当激励幅值p*=14.948 N/m时，响应幅值趋紧于0，即表现为该自激-受迫系统中不存在自激振动的形式。

图5 受激励幅值影响的自激振动幅值曲线

随着激励幅值的增加，气动荷载激励下的覆冰输电线自激振动条件被受迫激励所破坏，这种现象称为猝息。

对于施加受迫激励的自激系统，多采用幅频和相频响应曲线进行分析。为了验证本文幅频响应关系式推导结果的正确性，令激励频率Ω等于系统固有频率w，调谐参数σ=-0.8、0、0.8，用数学软件Maple绘出式(22)的幅频响应曲线。运用MATLAB求解式(8)得到激励幅值p*=3.736、7.472、11.210、14.948、18.68 N/m时的时程位移图，分别得到稳定时的振幅幅值如图6中的点a1、a2、a3、a4、a5。如图6所示。MATLAB求得的数值解和运用多尺度求得的幅频响应函数曲线吻合较好；并且发现σ=0.8时，随着激励幅值的变化，响应幅值会发生跳跃和多值现象；当响应幅值大于2时，幅频响应曲线的精确度也会随着激励幅值的增大而降低。

图6 激励幅值-响应幅值曲线

4 线路参数分析

风速对覆冰输电线舞动有非常大的影响，甚至可以决定覆冰输电线形成自激振动的条件。对于施加弱激励的自激系统，为了研究其非线性共振特性，用Maple数学软件绘出方程式(22)的函数曲线。激励幅值p*=0.186 8 N/m，风速U=4，8，12，16，20 m/s时系统的幅频响应曲线如图7所示。实线表示稳定，虚线表示不稳定。随着风速的不断增大，响应幅值也不断增大，从风速U=4 m/s的点p4增加到U=20 m/s的点p20；稳态解的不稳定区域也逐渐变大，从风速U=8 m/s的r1区域依此变化到U=12，16，20 m/s的r2，r3，r4区域；并且导致非线性也不断增强，自激-受迫系统呈现硬弹簧特性更加明显。

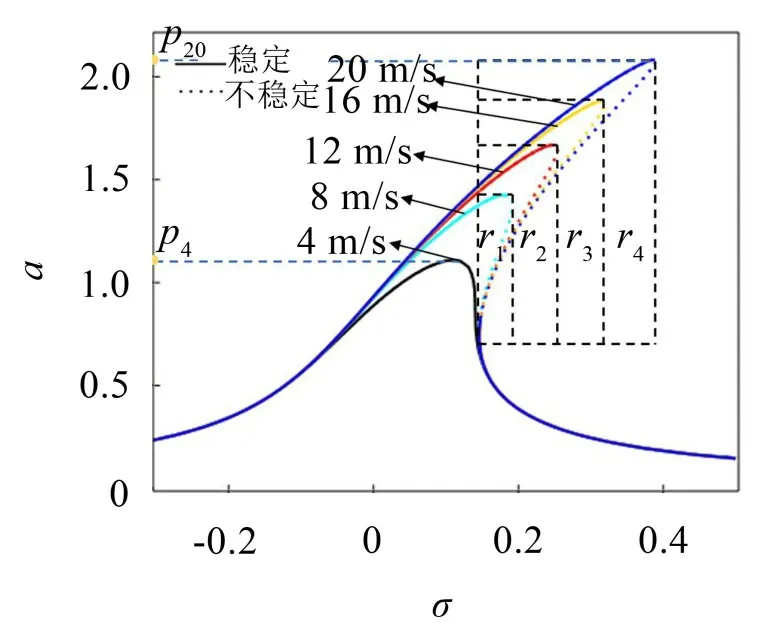
图7 不同风速的幅频响应曲线

为了弄清楚激励幅值对自激振动的影响，令式(22)的激励幅值p*=1.121、2.802、5.604、14.944 N/m，风速U=4 m/s，受迫激励项的频率Ω=w，并且运用Maple得到图8。

图8 不同激励幅值对应的幅频响应曲线

如图7所示。随着激励幅值增大，系统的响应幅值也逐渐增大，也就表明周期荷载激励项对响应幅值有着直接的影响。

风速和激励幅值的增大，都能使得响应幅值增大；由于风速表现为非线性舞动方程中负阻尼项，因此风速的增加又使得覆冰输电线舞动的非线性特征增强。

为了分析在相同线路参数和相同气动荷载情况下张力和垂度对覆冰输电线舞动特征的影响。取激励幅值p*=0.934 N/m，风速U=4 m/s；引用文献[18-19]中垂度与张力之间的公式d=mgl2/8H，取张力分别为H=15 000、20 000、25 000、30 000、40 000、50 000、60 000、70 000 N，分别对应于图9中A、B、C、D、E、F、G和H幅频曲线。使用MAPLE绘出式(22)的函数曲线，得到不同张力对应的幅频响应图。如图9(a)所示，随着张力从15 000 N增大到30 000 N，响应幅值从a15增加到a30；如图9(b)所示，随着张力从30 000 N增大到70 000 N，响应幅值a30从减小到a70；张力由小变大，垂度不断变小，自激-受迫系统的响应幅值出现先增大，后减小的现象，因此在工程应用中，适当增加输电线的张力可以减小覆冰输电线的舞动幅值。

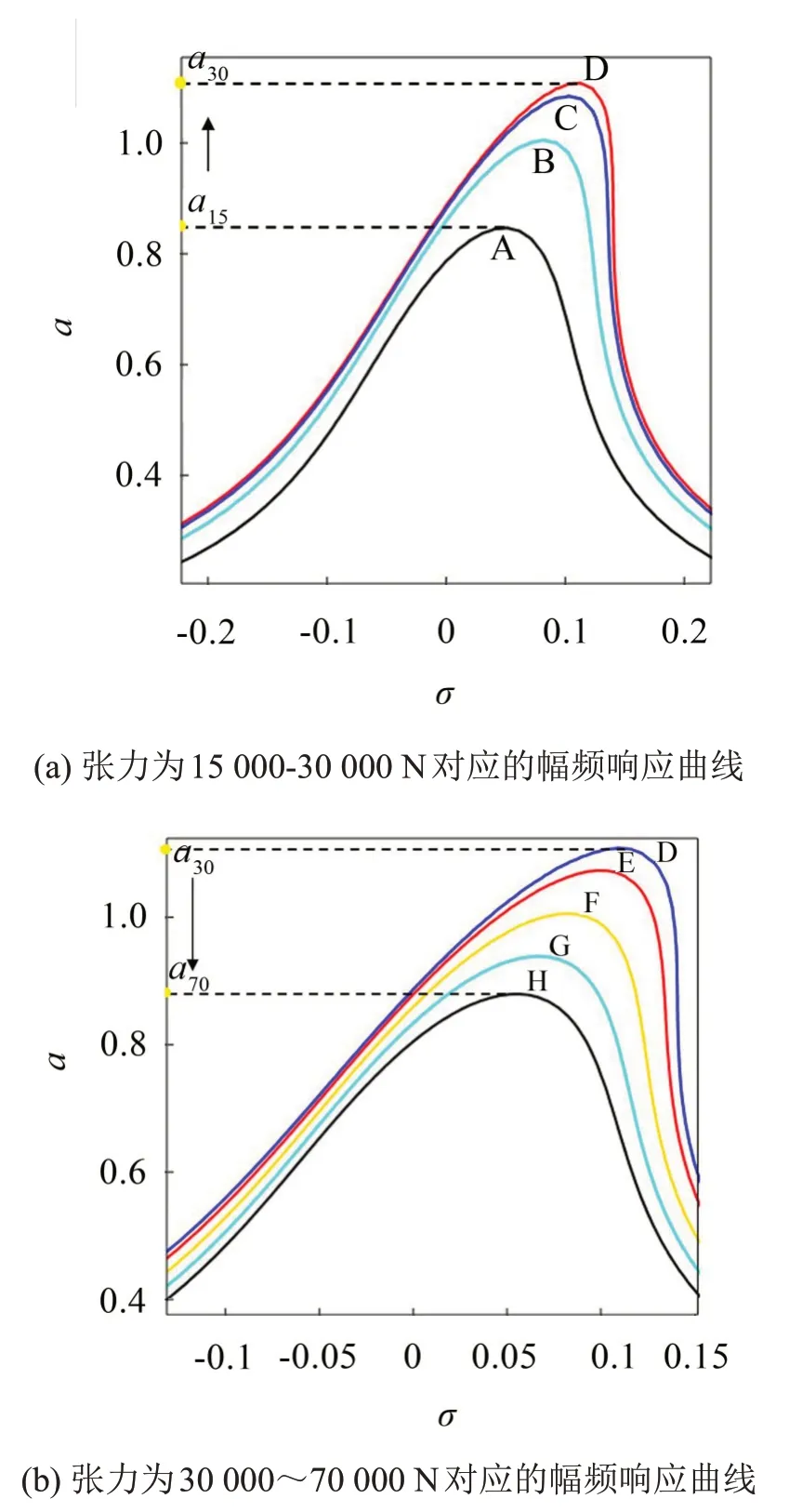
图9 不同张力对应的幅频响应曲线

为了分析输电线弹性模量变化对弱激励下自激系统的非线性特征影响，对于幅频函数式(22)，取张力H=30 000 N，垂度d=1.539 3 m，激励幅值p*=0.934 N/m，风速U=4 m/s；弹性模量为：E=9 560.7、47 803.3、239 016.5、478 033、2 390 165 N/mm2，分别对应着图10中A、B、C、D、E曲线。如图10(a)所示，弹性模量由小变大，输电线结构刚度不断增加，输电线舞动的幅值逐渐减小，使得自激-受迫系统非线性增强趋向于硬弹簧特征；随着弹性模量增大到239 016.5 N/mm2即曲线C时，系统的非线性特性随即开始减弱，幅值也随着变小，然而响应幅值产生跳跃、多值和不稳定现象。

图10 不同弹性模量和张力对应的幅频响应曲线

为了弄清楚输电线不同张力情况下，弹性模量变化对自激-受迫系统非线性特征的影响，如图10(b)，取张力H=20 000 N，d=2.309 0 m；如图10(c)，取张力H=50 000 N，垂度d=0.923 6 m。弹性模量E=9 560.7 N/mm2对应图10中曲线A的共振峰值，其中图10(b)的共振峰值最大，图10(c)的峰值最小；弹性模量E=478 033 N/mm2对应图10中曲线D的共振峰值，然而图10(c)的共振峰值最大，图10(b)的共振峰值最小；则表明在相同的线路参数、环境参数、以及相同弹性模量范围内，张力越大，响应幅值变化幅度越小。

从图10中也可以看出，从张力为20 000 N的图10(b)到张力为30 000 N的图10(a)，再到张力为50 000 N的图10(c)，随着弹性模量的增加，自激-受迫系统的硬弹簧特性也更加明显，响应幅值产生跳跃、多值和不稳定的现象增加。

弹性模量的增大能有效降低输电线舞动的共振幅值；增大弹性模量，同时增大输电线的张力，也能降低输电线舞动的共振幅值，然而随着张力的增大，自激-受迫系统的响应幅值出现了跳跃、多值和不稳定的现象。

5 结语

(1)当自激-受迫系统中激励幅值不断增大，其中自激振动幅值会越来越小甚至消失出现猝息现象，自激-受迫系统由自激振动和受迫振动叠加的振动形式转变为受气动荷载负阻尼影响的受迫振动。

(2)对于自激-受迫系统，风速的不断增大，使得系统呈现硬弹簧特性，并且导致系统非线性也不断增强，不稳定区域也逐渐变大；输电线张力和弹性模量同时由小变大，输电线结构刚度不断增加，也能有效地减小输电线舞动共振幅值，然而该系统也伴随着非线性特征的出现；因此适当增加输电线张力和弹性模量有利于减小输电线舞动的共振幅值。