车载设备悬吊位置及悬挂参数对车辆系统的影响

肖乾，李妍铭，罗志翔

（1.华东交通大学 运载工具与装备教育部重点实验室，南昌 330013；2.中车株洲电力机车有限公司 大功率交流传动电力机车系统集成国家重点实验室，湖南 株洲412001)

快速市域列车作为服务于大都市市域范围内的城市轨道交通工具，因其速度比地铁快、安全系数高、节能环保性强等特点而得到了广泛应用。在车辆运行过程中，车载设备与车体会发生耦合振动，若不选择合适的悬吊位置及悬挂参数，将会使车体地板面振动加剧，影响到整车的乘坐舒适性，因此对列车车载设备悬吊位置和悬挂参数进行研究，具有较大的理论价值和工程实际意义。

在车载设备悬吊位置的研究方面，国内机构和学者进行了较为广泛的研究[1-5]。其中，范乐天等[1]主要从悬挂设备功能的实现和车体重量的平衡角度分析了高速动车组车下设备的分布位置。吴娜等[2]建立了基于弹性车体的某高速动车组刚柔耦合模型，模型中不考虑设备的激励，探讨了车下设备的布置形式对车辆动力学特性的影响。

在车载设备悬挂参数研究方面，也进行了大量研究[3-6]。罗光兵等[7]建立了高速列车车辆垂向动力学模型，模型中不考虑设备的激励，研究了车下设备弹性悬挂参数与车体振动的关系。赵春等[8]基于SIMPACK软件建立了考虑弹性车体的高速客车刚柔耦合系统动力学模型，模型中不考虑设备的激励，研究了车下设备悬挂参数对车辆振动的影响规律。尤泰文等[9]研究了不同吊挂方式及刚度对车体垂向弯曲频率的影响。匡成骁等[10]研究一个镟轮周期内车载设备不同悬吊参数对车体振动的影响。贺小龙等[11-12]建立了车体-设备的27自由度刚柔耦合模型，对不同悬挂频率、不同悬吊位置、有无车辆设备这3种情况下乘客垂向乘坐舒适性的问题进行探讨。

从以上研究可以看出，研究人员通常以单个激励源的车载设备为对象，对高速列车悬吊位置和悬挂参数进行优化研究，但对于车载设备带有多个激励源、且车辆运行速度相对高速列车偏低的市域车而言，研究得还较少。因此，本文以市域车车载设备悬吊位置和悬挂参数优化研究为目标，引入刚柔耦合动力学理论来研究市域车不同悬吊位置和悬挂参数与车辆之间的动力学关系。

1 刚柔耦合系统动力学理论

许多学者基于矩阵缩减理论提取整备车体模态，采用SIMPACK和ANSYS建立基于弹性车体的刚柔耦合系统动力学模型，但由于矩阵缩减法只能生成近似的质量矩阵和阻尼矩阵[13]，计算结果存在一定误差。本文借助多体动力学软件UM，采用Craig-Bampton固定界面模态综合法[14]（简称C-B法）模拟复杂的弹性体模型。弹性体的特征模态由下式(1)求出：

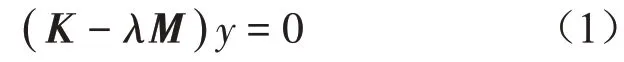
式中：K为刚度矩阵，M为质量矩阵，λ为特征值，y为特征模态。

采用模态矩阵H计算广义质量矩阵和广义刚度矩阵：

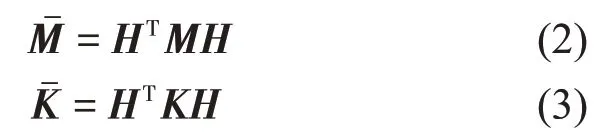
由式(2)和式(3)可知，计算出的和具有对角形式，再进行正则化处理：

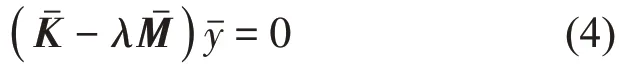
模态转变基于以下公式进行：

刚柔耦合系统动力学方程可表示为

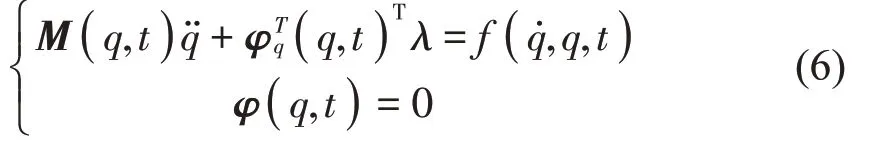
式中：M(q,t)∈Rn×m为广义质量矩阵，q∈Rn为广义坐标向量，λ∈Rm为Lagrange乘子向量，f(,q,t)为广义力向量，φ(q,t)为约束的代数方程列阵，φq(q,t)为雅可比矩阵。

2 刚柔耦合系统动力学模型建立

2.1 动力学模型拓扑图

本文研究的某160 km/h快速市域车主要由1个车体（含有车载设备）、2个构架、8个轴箱、4个轮对、一系悬挂系统和二系悬挂系统组成，快速市域列车拓扑示意图如图1所示。

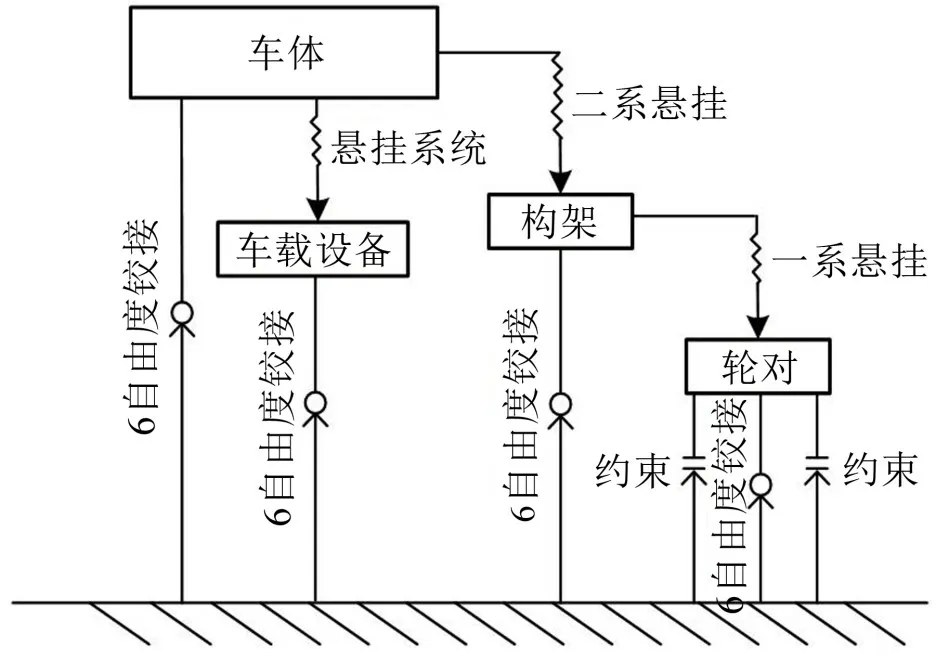
图1 动力学模型拓扑关系

2.2 刚柔耦合动力学模型建立

首先，建立弹性车体模型，弹性车体模型比刚性车体模型更能够真实反映车体的实际结构。根据车辆系统实际结构参数，采用UG软件建立市域车头车车体的几何模型，并导入HYPERMESH的前处理中获得车体的有限元模型，采用四节点壳单元SHELL181进行离散，顶盖边梁、内装和设备窗等采用质量点MASS21进行离散，整个头车车体模型划分为1 52 527个单元，874 515个节点，得到车体有限元网格模型并导入ANSYS软件中，采用C-B法对车体有限元模型进行弹性化处理。为了验证弹性车体模型的准确性，本文采用Block Lanczos求解器计算得到车体前21阶自由模态值，去除前6阶刚体模态值，对比自由模态值与正则化转换成弹性车体模型之后的模态值，见表1。发现最大误差处于2 %之内，这个计算结果能够用于指导工程实践，证明弹性车体模型建立的准确性较高。

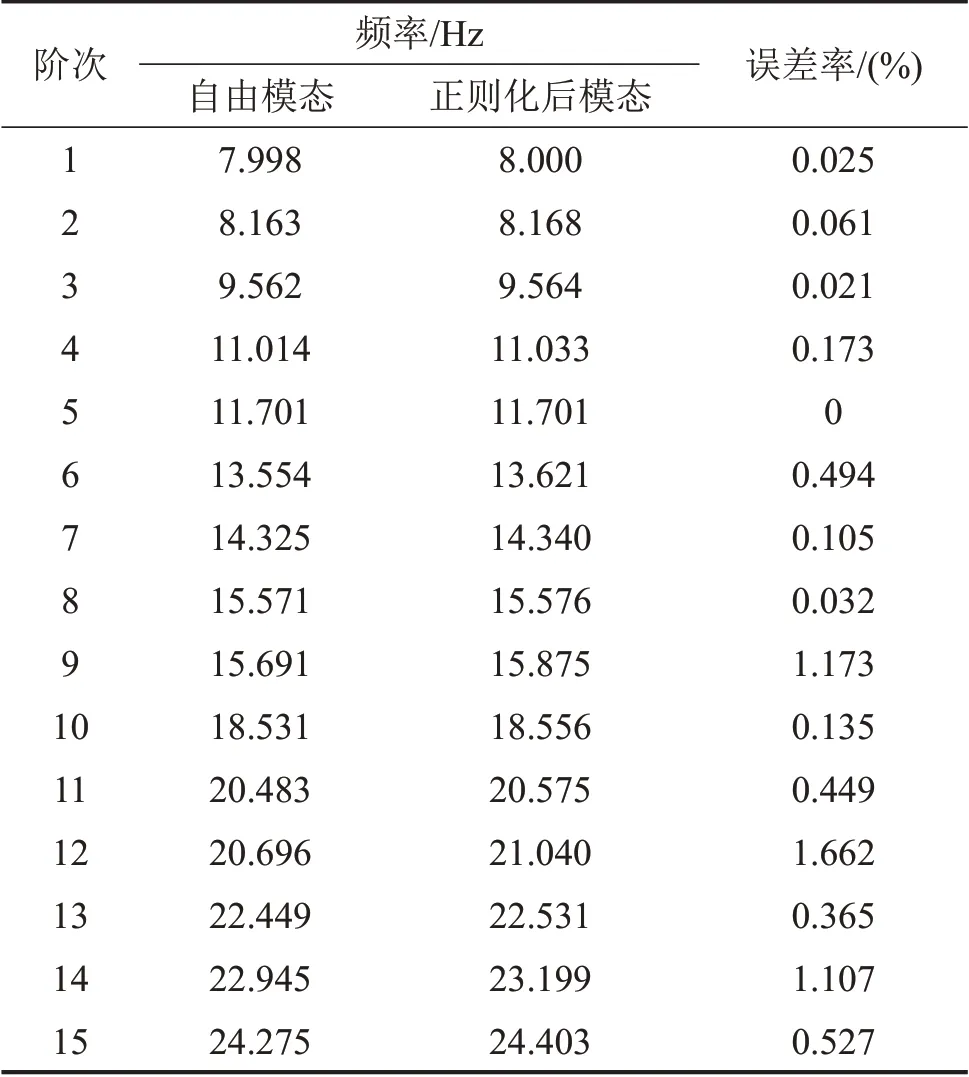
表1 模态对比

再次，在UM前处理软件中建立前、后转向架模型，并设置轨道不平顺。通过线性有限元子系统模块将前后转向架模型导入弹性车体模型文件，并借助UM软件将完整的车载设备模型加入到弹性车体模型。由于本文主要研究的是车载设备悬吊位置与悬挂参数的优化设计，因此将质量比较重、体积比较大的设备作为重点研究的对象。本文选取辅助变流器、前后空调以及悬挂梁（由于悬挂在横梁上的辅助制动、低压箱与横梁采用螺栓刚性连接，且此横梁只悬挂了这两个设备，因此将其作为一个整体进行研究，并将这个整体简称为悬挂梁）为重点研究对象，将其作为刚体处理，而其它设备如：辅助风缸、开闭机构、贯通道等将重点以考虑车载设备质量而基本忽略转动惯量的质量点形式加载到弹性车体上。车载设备与车体均采用刚性连接方式。车轮采用LM型面，钢轨采用CHN60型面，考虑到计算速度和精度，选用FASTSIM算法进行轮轨之间的滚动接触计算。图2所示为包含车载设备的刚柔耦合系统动力学模型，模型中考虑了车体的弹性振动和具有6个自由度的车载设备。

为验证计算模型的准确性，采用UM软件计算该模型在运行平稳性、乘坐舒适性、运行安全性3个方面的动力学性能。计算平稳性和舒适性指标时，车辆以160 km/h的车速匀速运行1 000 m，车体振动加速度采集按照GB 5599-1985规定的方法进行设置，测点位置如图3所示（X为纵向，Y为横向），选择测点A和C计算运行平稳性指标，选择测点F计算乘坐舒适性指标，计算结果见表2。分析得：A点和C点处横向平稳性和垂向平稳性指标值都在GB 5599-1985规定的安全限值内，且处于“优”级；车体中心F点的舒适性指标处于UIC513－1994中的“最佳”级，车辆直线运行平稳性及舒适性指标满足国家标准。计算车辆运行安全性指标时，以转向架1位和2位轮对左侧轮为研究对象，计算其在曲线工况下的轮重减载率、轮轴横向力、脱轨系数、轮轨横向力、轮轨垂向力这几个关键性指标，计算结果见表3。

表2 平稳性和舒适性指标值

表3 曲线工况下各指标最大值

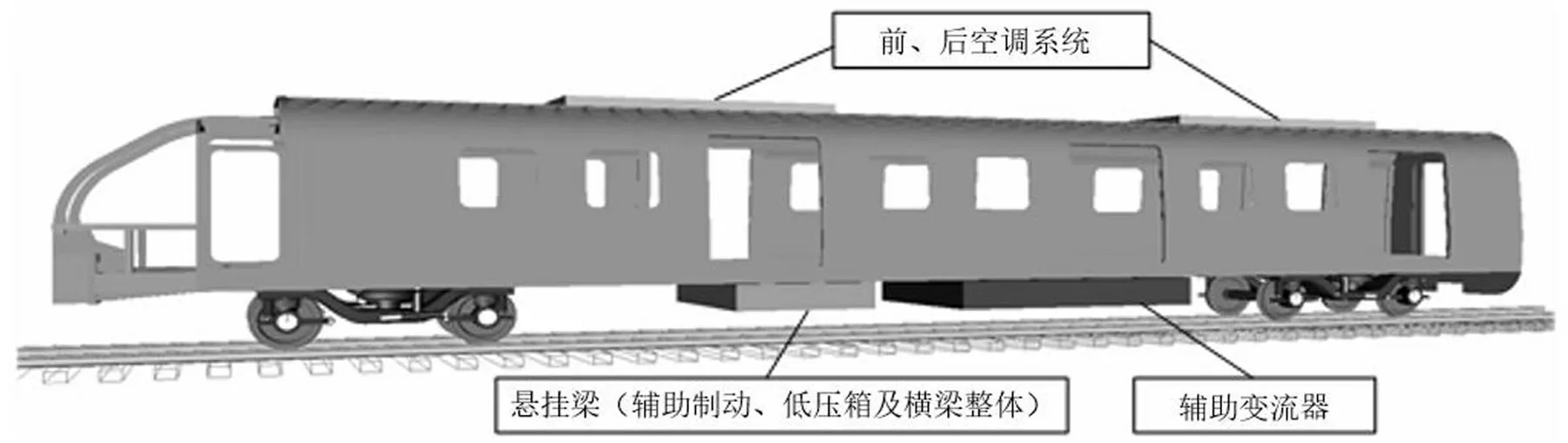
图2 基于弹性车体的市域车车辆-轨道刚柔耦合系统动力学模型

图3 加速度测量点位置

分析得：轮重减载率的最大值为0.504，小于GB 5599－1985所规定的0.65；轮轴横向力的最大值为21.205 kN，小于根据GB 5599－1985所计算的46.433 kN；脱轨系数的最大值为0.280，远小于GB 5599－1985规定的1.0，也小于TB/T2360－1993规定的0.6；轮轨横向力的最大值为17.837 kN，小于根据GB 5599－1985所计算的46.802 kN；轮轨垂向力的最大值为87.24 kN，远小于国标准规定的170 kN。综上得，所建计算模型动力学特性满足相关国家标准，可以用于动力学仿真计算。

3 车载设备不同悬吊位置对车辆动力学特性的影响

3.1 辅助变流器悬吊位置对车辆动力学特性的影响

以辅助变流器为对象，只考虑辅助变流器的激励，空调处于关闭状态，其它设备处于建模原始位置，研究辅助变流器悬吊在车体底架不同纵向位置对车辆动力学特性的影响规律。辅助变流器的纵向悬吊位置以其质心纵向位移为考察对象，辅助变流器与车体连接点设置为4个（前后各2个）。

图4、图5是随着辅助变流器从车体后端向前端移动，车体前、中、后端平稳性指标的变化规律。分析可得：随着辅助变流器从车体后端向前端移动，车体前端横向平稳性指标在高、低速下都逐渐变好；中部横向平稳性指标在低速时变化不大，在高速时逐渐变差；后端横向平稳性指标在低速下逐渐变差，在高速下先变好再逐渐变差，在变差转折点时，辅助变流器质心的纵向位移为-1.265 m左右。对于车辆垂向平稳性指标，随着辅助变流器从车体后端向前端移动，车体前端垂向平稳性指标逐渐变好；车体中部、后端垂向平稳性指标在低速下逐渐变好，高速下逐渐变差，160 km/h下车体中部垂向平稳性曲线在位置2 m附近有“突变”，这可能是由于辅助变流器缓慢移动时，车体与辅助变流器在此位置发生共振，从而引起垂向平稳性指标急剧增大的现象；车体后端垂向平稳性曲线在80 km/h和120 km/h下趋势相反，这可能是由于车载设备悬吊位置与车辆运行速度不同引起车体振动情况不同，动力学平稳性指标有所不同，导致两种速度下平稳性曲线趋势相反。辅助变流器悬吊位置越靠近车体前端对车体前端的平稳性指标越有利，对车体中部及后端平稳性指标越不利；当悬吊位置靠近车体后端时，车体前端的运行平稳性变差，在160 km/h和120 km/h速度下的车体后端横向平稳性变差。

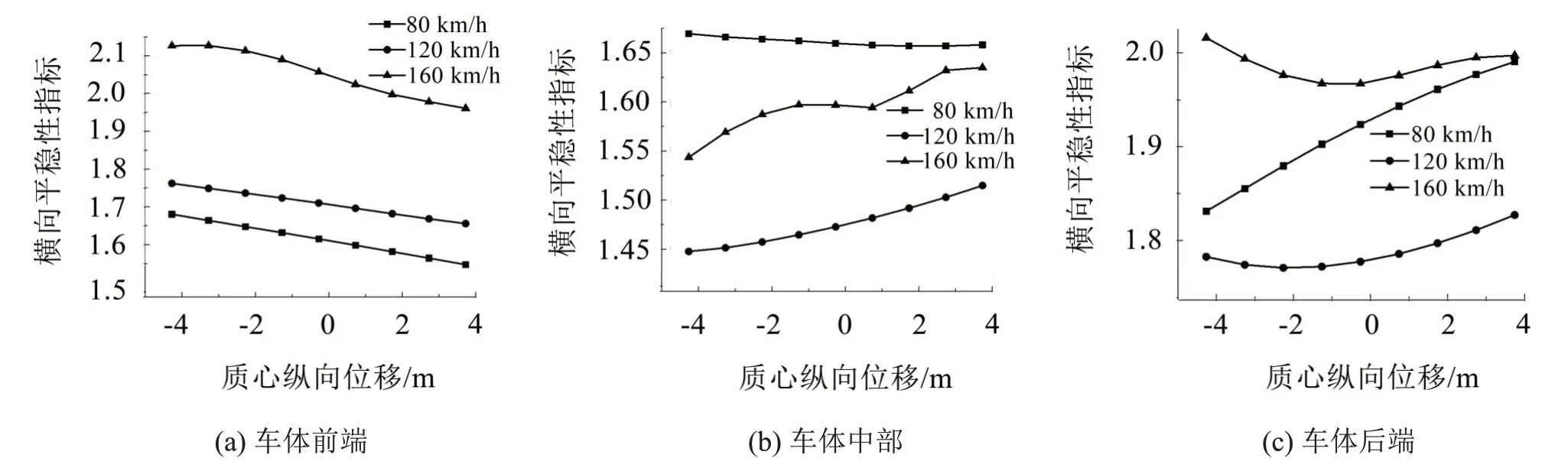
图4 横向平稳性指标

图5 垂向平稳性指标

3.2 悬挂梁悬吊位置对车辆动力学特性的影响

将横梁位置的移动看作是悬挂梁刚体质心的移动，研究刚体质心纵向位移的变化对车辆动力学性能的影响。图6、图7是随着悬挂梁从车体后端向前端移动，车体前、中、后端平稳性指标的变化规律。分析得：随着悬挂梁质心纵向位移从-4.8 m向5.2 m移动，车体前端横向平稳性指标逐渐变好，垂向平稳性指标在高速下逐渐变好；垂向平稳性指标在高速下先变好后趋于平缓；车体后端横向平稳性指标在低速下逐渐变差，垂向平稳性指标在高速下逐渐变好。

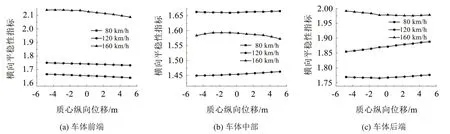
图6 横向平稳性指标

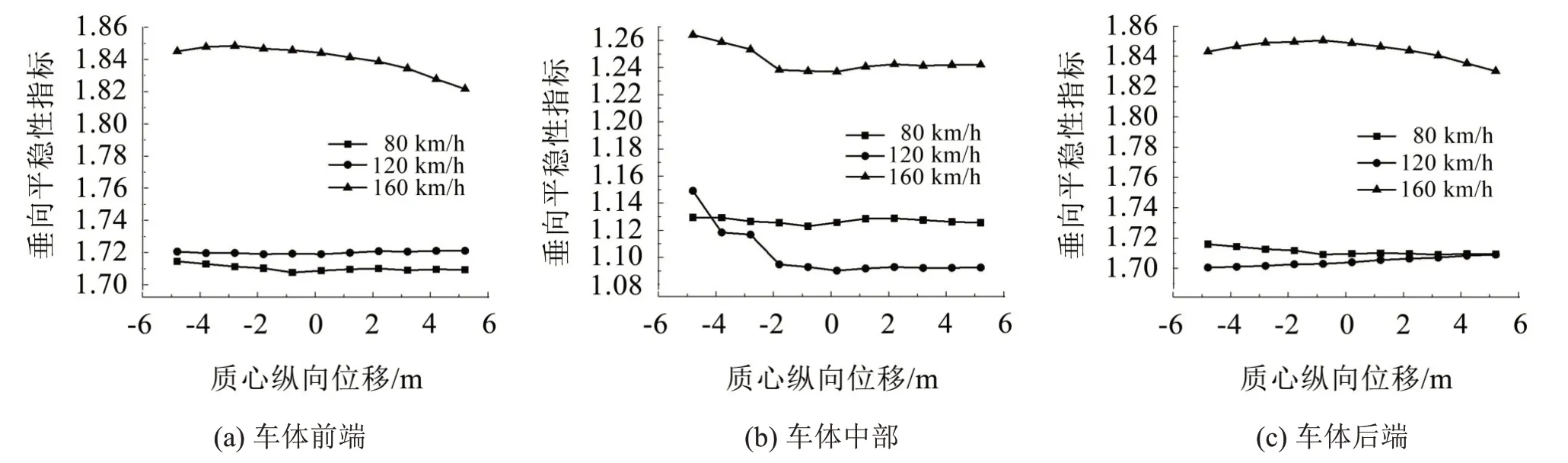
图7 垂向平稳性指标

4 不同悬挂参数对车辆系统振动的影响

4.1 悬挂刚度对车辆系统振动的影响

（1）辅助变流器悬挂刚度对车体振动的影响

图8列出了辅助变流器横向、垂向悬挂刚度对车体中部地板振动的影响。分析可得：120 km/h时车辆系统可能出现反共振从而导致120 km/h时车体横向振动最小。随着辅助变流器横向悬挂刚度的逐渐增大，车体地板面振动逐渐增大，但当刚度≥0.5 MN/m时，继续增大横向刚度对车体地板面的振动基本没有影响，当车辆以120 km/h运行时，刚度较低对应的车体地板面振动越大，振动突变点刚度值为0.2 MN/m。当刚度逐渐降低时，辅助变流器自身的振动也会加剧，因此，辅助变流器横向刚度的最优区间应选为0.2MN/m～0.5 MN/m，垂向悬挂刚度应选为1 MN/m～2.6 MN/m。

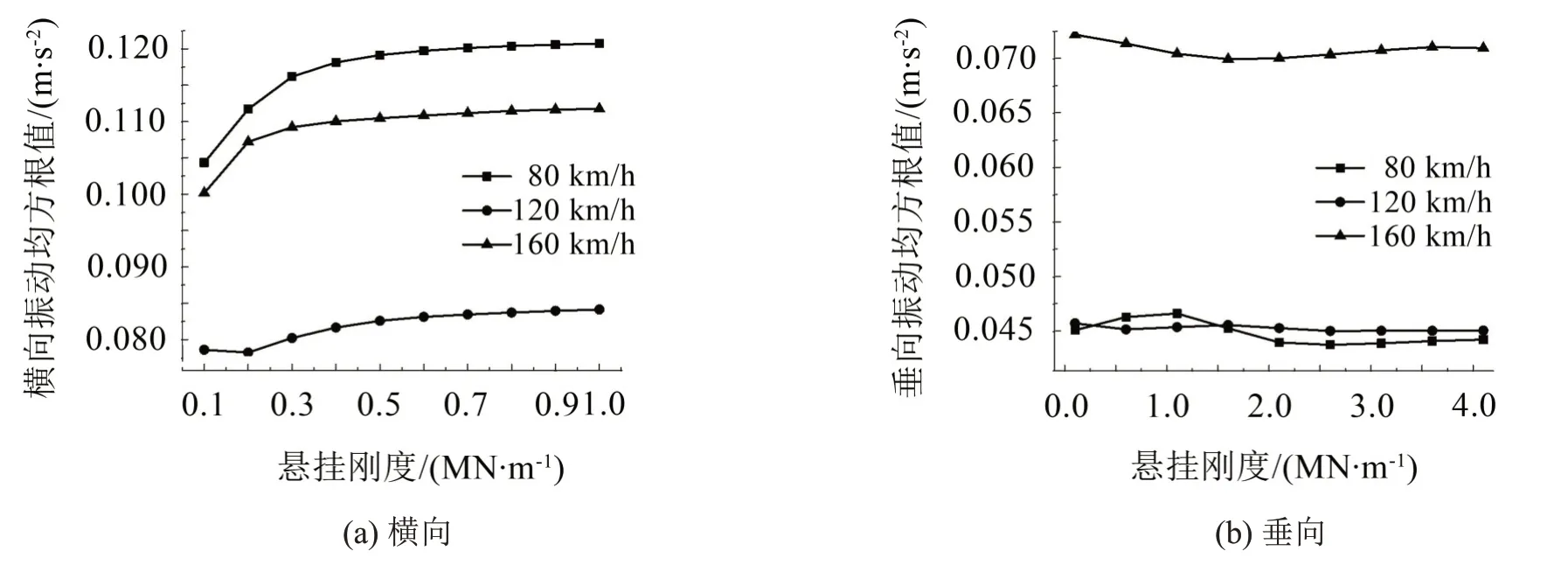
图8 车体中部振动加速度均方根

（2）空调悬挂刚度对车体振动的影响

图9是空调横向、垂向悬挂刚度对车体中部地板面的振动特性。分析可得：随着空调横向悬挂刚度从0.01 MN/m增加到0.21 MN/m，车辆系统的横向振动在0.07 MN/m之前急剧增大，在0.07 MN/m之后趋于平缓并略有减小。随着空调垂向悬挂刚度的增大，车体中部振动先缓慢增大后急剧增大。综合考虑，空调系统横向悬挂刚度的最优区间为0.01 MN/m～0.07 MN/m，垂向悬挂刚度最优区间为0.1 MN/m～0.5 MN/m。

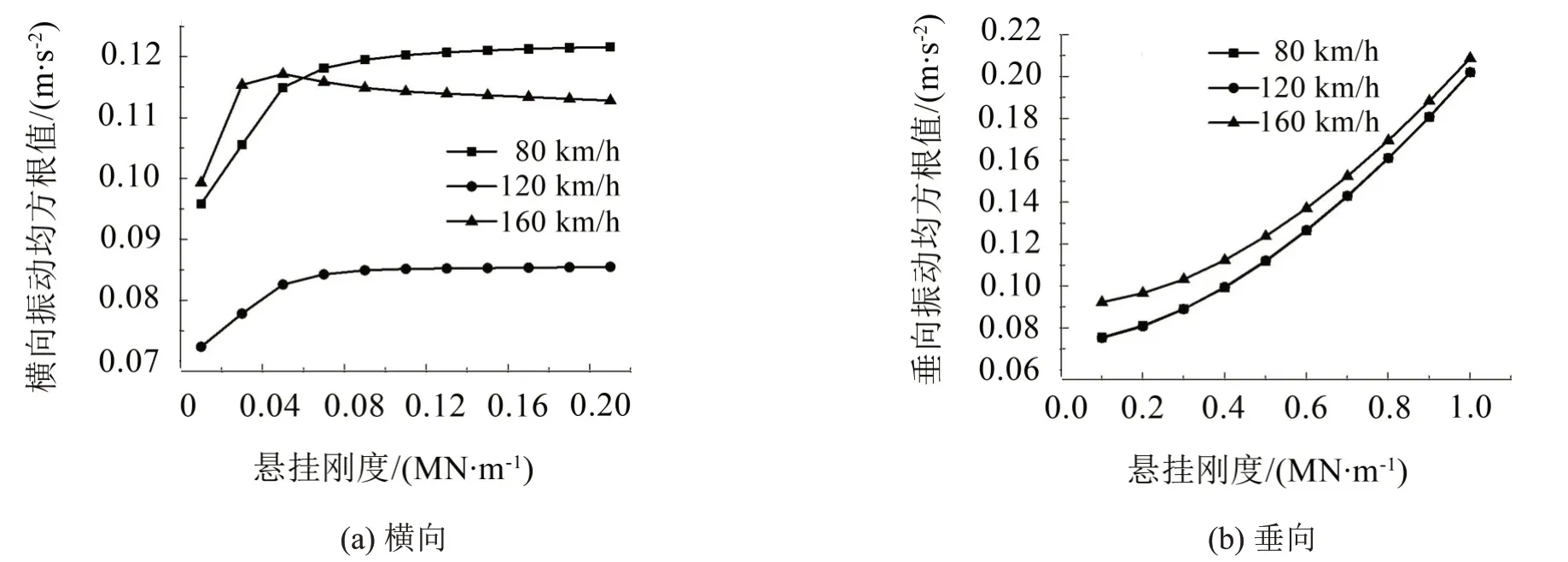
图9 车体中部振动加速度均方根

4.2 悬挂阻尼比对车辆系统振动的影响

（1）辅助变流器悬挂阻尼比对车体振动的影响

图10、11分别是辅助变流器悬挂阻尼比对车体中部地板及设备本身振动的影响。分析可知：随着阻尼比的增大，车辆地板面的振动逐渐减小。当悬挂阻尼比接近零时，车体地板面的振动将会恶化，因此阻尼比的取值应尽可能远离零。当阻尼比达到0.1左右时，继续增大阻尼比，对车体中部地板面的横向和垂向振动变化不大。从图11可看出当阻尼比在0.1以上时，继续增大阻尼比对设备的振动起到一定的抑制作用，但阻尼比增大会引起橡胶减振器的发热量增大，容易老化蠕变，因此，辅助变流器的最优悬挂阻尼比为0.1，最优悬挂阻尼比区间为0.08～0.12。

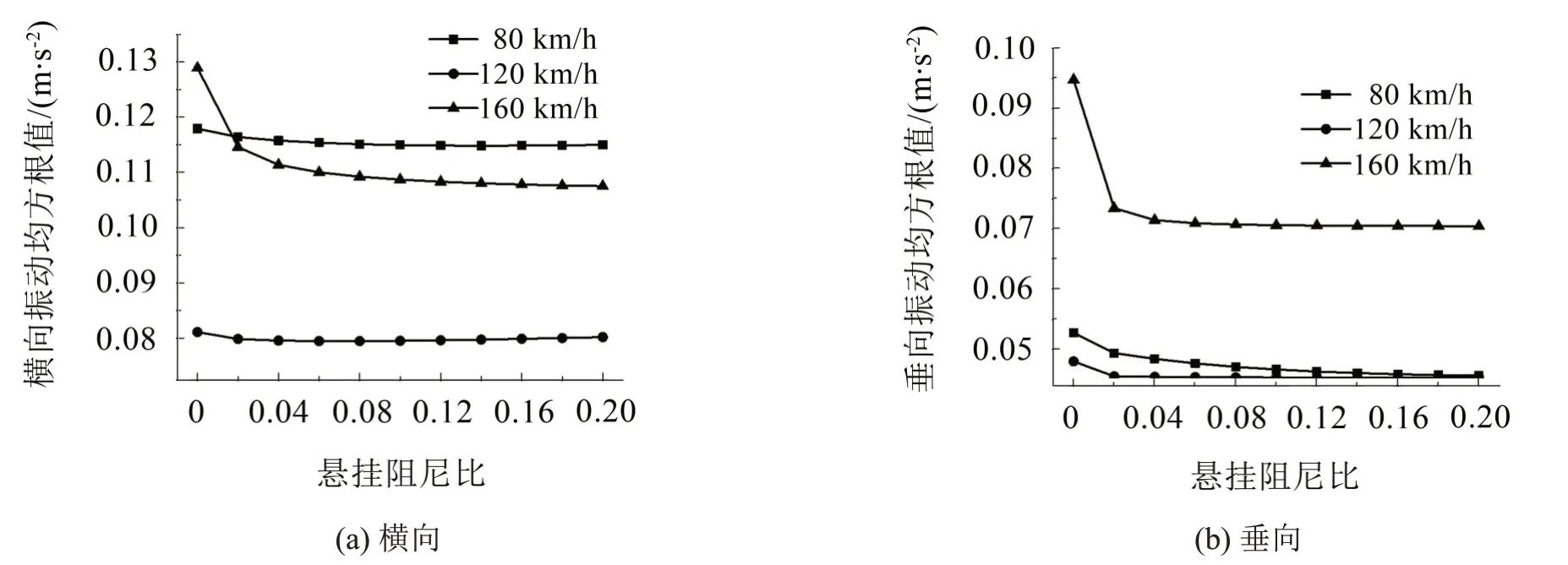
图10 车体中部振动加速度均方根

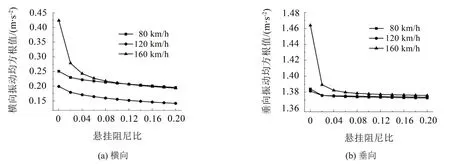
图11 设备中心振动加速度均方根

（2）空调悬挂阻尼比对车体振动的影响

图12为空调悬挂阻尼比对车体中部地板的影响。由图得：空调不同悬挂阻尼比对车体地板面的横向振动和垂向振动都会产生一定的影响，但对垂向影响大于横向。随着悬挂阻尼比的逐渐增大，车体地板面的横向振动先减小后基本不变，车体地板面的垂向振动在阻尼比0.04之前逐渐减小，在0.04～0.2时逐渐增大。综合考虑车辆系统的振动特性，空调悬挂系统的最优阻尼比为0.04，最优区间为0.02～0.06。

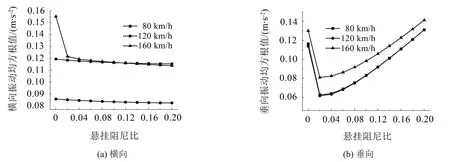
图12 车体中部振动加速度均方根

5 结语

本文通过建立车辆-轨道刚柔耦合系统动力学模型，分析了车载设备悬吊位置对市域车动力学特性的影响及辅助变流器和空调的悬挂刚度、悬挂阻尼比对车辆系统振动的影响，求出车载设备最优悬吊位置区间与最优悬挂参数区间，得出以下结论：

（1）辅助变流器纵向位置应处于车体中心偏后位置，当辅助变流器质心纵向位移处于-3.5 m～-1 m时，车辆直线运行平稳性能最佳；悬挂梁在车体纵向悬吊位置不同对车辆在高速运行下动力学特性影响较低速时更大，质心纵向位移在1 m～5 m时，整车的动力学性能最佳；

（2）辅助变流器各参数最优区间值：横向刚度为0.2 MN/m～0.5 MN/m，垂向悬挂刚度为1 MN/m～2.6 MN/m，悬挂阻尼比为0.08～0.12；空调系统各参数最优区间值：横向刚度为0.01 MN/m～0.07 MN/m，垂向悬挂刚度为0.1 MN/m～0.5 MN/m，阻尼比为0.02～0.06。