基于空间近邻关系的非平衡数据重采样算法
2021-06-16李睿峰李文海孙艳丽吴阳勇
李睿峰,李文海,孙艳丽,吴阳勇
海军航空大学,烟台 264001
非平衡数据的分类问题已经成为当今许多数据密集型应用中一个关键的研究方向[1],例如信用卡欺诈数据[2]、网络入侵[3]、金融工程[4]、生物医学数据分析[5]和设备故障检测[6]等. 这类应用中的少数类样本通常蕴含重要的信息,是数据分析的重要目标,其已成为数据挖掘研究的热点之一[7].例如在设备故障检测应用中,不平衡的测试数据广泛存在,通常正常样本的数据量要远远大于故障样本[8]. 由此导致使用传统的故障诊断方法训练所得的结果分类器对正常样本产生很高的检测率,对故障样本的检测和隔离效果却很差,而故障样本的检测率在故障诊断领域中更有意义,也更为重要.
目前,机器学习和数据挖掘领域针对不平衡数据集的处理思路[9]主要有两大类:改进算法[10]以适应非平衡数据集,或者对数据集进行重构[1]以适应现有的分类算法. 改进算法是指在算法层面进行改进以适应非平衡学习问题,如代价敏感学 习[11]、 支 持 向 量 机[12]( Support vector machine,SVM)、集成学习[13]等. 通过修改算法中的代价敏感信息以适应数据不平衡,但也面临着一些问题,如修改算法后如何避免分类性能恶化,多类分类问题的代价敏感信息确定困难等[14]. 数据集重构也称为重采样方法,它在不修改分类算法的情况下修改训练数据集的大小,可容易地应用于任何分类算法. 重采样方法利用少数类样本过采样和多数类样本欠采样两种手段[15],人为调整实例数量来平衡数据集的分布. 欠采样主要包括随机欠抽样[16]、单边选择[17]、近邻清理[18]和基于欧氏距离的随机欠抽样[19]等方法,过采样主要有随机插值、先验复制[14]和合成少数类过采样技术[20-21](Synthetic minority oversampling technique,SMOTE)等方法. 由于单独采用欠采样方法可能导致样本信息丢失,单独采用过采样方法可能导致分类器出现增加时间开销、过拟合现象等问题,于是人们较多采用混合采样的非均衡数据处理方法[7]. 包括谷琼等[22]提出的一种基于SMOTE-Clustering的混合采样算法;冯宏伟等[7]提出的基于“变异系数”的边界混合采样方法(Boundary mixed sampling,BMS);陶新民等[23]提出的基于随机欠采样(Random under-sampling,RU)与 SMOTE相结合的SVM算法等.
由于人为地增加样本或者减少样本都不可避免的会导致噪声点增加并损失数据原有信息,从而降低分类精度,因此合理的过采样和欠采样方法是重采样方法的核心. 为了对数据集做有效的均衡化处理,本文提出了一种基于样本空间近邻关系的重采样(Resampling based on neighbour Relationship,RBNR)方法. 本方法首先根据数据集中少数类样本的空间近邻关系进行安全级别评估[24],根据安全级别有指导的进行SMOTE升采样;然后对多数类样本依据其空间近邻关系计算局部密度[7],从而对多数类样本密集区域进行降采样处理. 采用十折交叉验证的方式产生训练集和测试集,在对训练集进行重采样之后,以核超限学习机(Kernel extreme learning machine,KELM)[25]作为分类器进行训练,并在测试集上进行了验证.
1 基本算法与相关定义
1.1 核超限学习机


与传统ELM相比,KELM无需设置映射函数和隐层神经元数量,人为干预更少,能有效避免隐层神经元随机赋值导致的泛化性和稳定性降低的问题. 同时,KELM又继承了传统ELM在处理分类任务上的优势:①以最小化训练误差和输出权重范数为训练目标,相对于其它传统人工神经网络(Artificial neural network,ANN)算法具有更高的泛化性能,从而抑制过拟合[14];②简洁高效的隐层结构能够大量压缩算法运行时间和内存空间开支[26-27].
1.2 安全级别
对少数类样本进行升采样,应当尽可能的接近样本原始分布,因此以安全级别指导SMOTE方法对少数类样本进行升采样.
1.3 局部密度
在非均衡数据中正负样本数量差异较大,在对少数类样本进行升采样时增加了样本总量. 于是,为控制数据集规模,可以适当减少样本密集区域的多数类样本. 因此,采用局部密度的概念[28]识别非均衡数据中多数类样本的密集区域.
定义1(k-距离)设D为数据集,k为任意正整数,定义对象p与对象o∈D之间的距离k_dist(p)=dist(p,o)为对象p的k-距离,满足条件:
①存在不少于k个对象q∈D{p},使得dist(p,q)≤dist(p,o);
②存在不多于k-1个对象q∈D{p},使得dist(p,q)<dist(p,o).
定义2(k-近邻)定义所有与p的距离小于等于k-距离的对象为对象p的k-近邻. 即:

定义3(局部密度)对象p与其k-近邻距离均值的倒数定义为该点的局部密度:
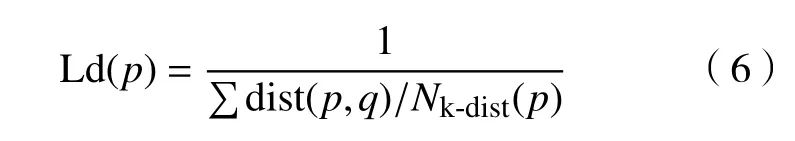
2 RBNR算法
RBNR重采样算法首先评估原始数据集中少数类样本的安全级别,基于其安全级别进行SMOTE升采样,从而增加少数类样本的占比;对于多数类样本,寻找出局部密度较大的区域,样本量二倍于降采样数量,进行随机减采样,从而对多数类子集进行约简. 算法流程如图1所示.

图1 RBNR算法流程图Fig.1 Flowchart of the RBNR algorithm


3 实验分析
3.1 评价指标
在非平衡分类问题的研究中,通常基于混淆矩阵(如表 1)来评价算法的性能[7],表 1中,TP,FN,FP,TN均表示个数.

表1 混淆矩阵Table 1 Confusion matrix
(1)召回率(又称查全率),表示正类(少数类)样本被预测正确的比例,即
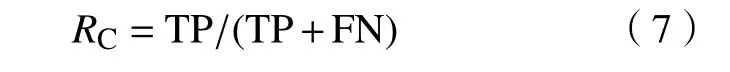
(2)F-value评价少数类的分类精度,定义如下:

其中,PR=TP/(TP+FP)为少数类样本的查准率(又称为精准率). 通常令调节参数 α =1.
(3)G-mean用以衡量算法对少数类和多数类进行分类的均衡程度,定义如下:

其中,PA=RC为真正率,NA=TN/(TN+FP)为真负率.
3.2 UCI数据集
UCI数据库是机器学习领域中使用最广泛的公开数据库之一,为客观验证所提算法的整体性能,选取其中具有非平衡性特征的数据集进行实验,数据集描述如表2.

表2 选用的UCI数据集Table 2 UCI data set
其中:CTG数据集为胎儿心电图数据,以“正常”为多数类,“病态”为少数类;Diabetes为糖尿病人的身体监测数据集,直接将两个类别分别作为多数类和少数类;Glass为玻璃类型分类数据集,以前四类作为多数类,后两类作为少数类;Wine数据集为三个不同品种的葡萄酒化学分析结果,将第1、2类合并为多数类,第3类作为少数类.
3.3 实验设计
(1)电路选型.
电子电路的测试和故障诊断技术对提升电子产品的可靠性、降低生产成本等方面具有重要意义[29],因此实验选取串联稳压电路(图2)作为应用案例来分析所提方法在电子电路故障诊断中的性能. 该电路包含20个可更换单元,共可产生58个硬故障,即各个元器件上的短路和开路故障. 在输入端施加信号幅度为10 V、频率为50 Hz的正弦波信号,从8个测试点上收集稳态电压信息,取电压值特征作为原始测试数据.

图2 串联稳压电路Fig.2 Serial regulating circuit
(2)实验环境.
依托实验室现有的激励、测试仪器,通过实物测量的方式,获取电路正常和故障状态下的测试数据. 测试环境如图3.

图3 测试环境图Fig.3 Testing environment
(3)测试数据集.
通过重复测试,共采集到188组正常状态下的样本,此后电路发生故障,电容1击穿,后采集了45组故障状态下的样本,特征维数为9(其中图中测试点1作为整流桥输出点,采集了其信号稳定后电压最大值V1_max和最小值V1_min,测试点2~8均采集了信号稳定后的电压有效值,即V2~V8),不平衡比为1∶4.17. 根据不平衡数据集分类问题的相关研究[7,9,12,22],该不平衡比例具有一定的代表性. 数据集记为Regulator,部分数据如表3.

表3 电路实测数据(部分)Table 3 Some circuit measured data
3.4 参数分析
将RBNR算法与SMOTE过采样方法、随机欠采样与SMOTE相结合的算法(RU-SMOTE)[23]和基于“变异系数”的边界混合采样方法BMS[7]进行对比实验,分类器均采用KELM. 在传统的面向分类问题的机器学习方法中,普遍采用最小化交叉验证分类误差的方式选取模型参数. KELM涉及到核函数、正则化参数与核参数的设置,借鉴文献 [26]~[27],核函数选用 RBF核,正则化参数C取值范围设定为{10-5,10-4,104,105},在训练样本间的最大欧式距离和最小欧式距离间等间隔取20个离散值作为核参数σ的范围(调用dd_tools工具箱的scale_range函数实现). 采用网格搜索法,以最小化交叉验证分类误差为目标,确定各参数.
由前文可知,RBNR算法为了使数据集分布均衡,根据两类样本的数量差,令升、降采样量相等.为公平起见,将RU-SMOTE算法和BMS算法中的升、降采样量也设为相等Nup=Ndown. SMOTE算法只包含升采样,令其升采样量与其他三种算法中少数类样本的升采样量设置为相同值,进而确定采样倍率Nsample=[Nup/Nmin]. 文献[20]将SMOTE算法中的最近邻阈值KSMOTE设置为采样倍率的2.5倍,因此在实验中将其设置为KSMOTE=[Nsample×2.5].RBNR算法涉及少数类样本近邻值和多数类样本近邻值两个参数,采用网格搜索法,最终确定k1=Nmin和k2=Nmaj/3时算法性能总体最优.

图4 BMS 算法参数分析. (a)RC 值分析;(b)F-valve值分析;(c)G-mean 值分析Fig.4 Parameter analysis of BMS: (a) analysis of the RC; (b) analysis of the F-valve; (c) analysis of the G-mean
3.5 结果分析
为消除随机因素的影响,取5×10折交叉验证的方式,每次实验前随机生成训练集和测试集. 在实验之前,运行一次交叉验证以确定正则化参数C和核参数σ,模型参数标注在最后一列. 计算50个结果中RC、F-value和G-mean有效数据的统计平均值,将最大值加粗表示;计算实验结果的标准差,将最小值加粗表示. 结果如表4.

表4 F-value和G-mean性能比较Table 4 Comparison between the F-value and G-mean
由实验结果可以得出以下结论:① 无论是选用UCI数据集还是电路实测数据进行训练,RBNR算法取得的RC均值、F-value均值和G-mean均值在绝大多数情况下是最高的. ②虽然在Wine数据集上,采用SMOTE算法得到的F-value均值和G-mean均值更高一些,但是RBNR算法的结果与之非常接近且更稳定(标准差最低),并且SMOTE算法得到的重采样数据集规模会很大,冗余数据给后续的分类器处理过程带来了较大的开销. ③在Regulator数据集上,采用RU-SMOTE算法得到的RC均值最高,但是其标准差也是最高的,说明该算法的稳定性较差;而且RU-SMOTE算法在Regulator数据集上取得的F-value均值和G-mean均值均为最低,说明该算法在提高少数类样本召回率的前提下没能兼顾到多数类,可能随机删除了一些重要的多数类样本;此外,其分类结果在其他数据集上表现也并不好. ④由于每次都随机产生训练集和测试集,从多次重复训练的结果来看,本文所提算法在多次交叉验证中所得RC、F-value和G-mean值的标准差大部分都是最低的(在个别不是最低的情况下也与最低值相差很小),说明算法性能较为稳定,在整体上具有更为优良的性能. ⑤在数据规模相当的情况下,RBNR普遍优于RU-SMOTE和BMS算法,且RBNR算法在某些数据集(Diabetes、Glass)上优势显著.
为了更直观的进行对比,将表4中的RC、F-value和G-mean值绘制了柱状图,如图5.

图5 结果对比柱状图. (a)RC 值对比;(b)F-value 值对比;(c)G-mean 值对比Fig.5 Bar graph of result comparison: (a) comparison of RC; (b) comparison of F-value; (c) comparison of G-mean
从整体来看,RBNR算法是明显优于其他算法的,其分类效果也更为稳定.
4 结论
数据挖掘领域的研究者们提出了大量的重采样算法用于解决数据集非平衡问题,而这一问题的关键就在于如何使得重采样之后的新数据集更接近真实的样本分布,因此本文提出了一种基于空间近邻关系的混合重采样算法RBNR来解决这一问题. 实验表明,以KELM作为分类器,RC、F-value和G-mean作为评价指标,RBNR的总体性能优于SMOTE、RU-SMOTE和BMS算法. 这是由于RBNR算法通过计算安全级别,以一种更接近少数样本原始分布的方式指导升采样,而不是像SMOTE算法一样随机扩充数据,也不像BMS算法一样只扩充边界少数类(事实上这种方法更容易引入噪声). 通过计算局部密度,约简多数类样本密集区域,从而更加合理的控制了数据规模. 这种根据空间近邻关系视情处理的方式,可以更加有效地均衡化原始数据集. 本文存在的不足在于只是针对二分类问题,后续将针对多类分类中的数据不平衡问题进行研究.
