基于虚拟材料复模量非均匀分布的螺栓连接薄板结构半解析建模
2021-06-16刘晓峰
刘晓峰,孙 伟✉,孙 悦
1) 东北大学机械工程与自动化学院,沈阳 110819 2) 东北大学航空动力装备振动及控制教育部重点实验室,沈阳 110819
螺栓连接由于结构简单、成本低、便于装拆且具有一定可靠性而被广泛应用. 现代航空发动机的连接结构亦多采用螺栓进行紧固连接. 螺栓连接结构相比于整体结构,其结合部处整体刚度会有所下降,且该部分会产生一定的阻尼作用,两者共同作用,从而对整个结构的力学特性产生影响. 因此,如何有效的模拟螺栓连接结构的结合部,对研究整个螺栓连接结构的力学特性至关重要.
近年来,很多学者致力于螺栓连接结构的力学特性研究,研究人员通常会建立精确地高保真模型进行螺栓结合部的静力学分析. 例如,Reid和Hiser[1]采用非线性有限元分析方法,建立了螺栓结合部在剪切荷载作用下单向滑动的模型,在一定精度上再现了物理实验中出现的力-位移滞回曲线. Sawa等[2]建立了螺栓连接结构的三维有限元模型,分析了考虑螺纹的螺旋应力分布和其分别在循环载荷和静载荷作用下的弹塑性变形状态. Luyt等[3]对两种圆形螺栓法兰装置进行了完整的有限元建模,可以准确地预测带有黏弹性垫圈的平面和凸起法兰组件在阀座状态下的蠕变松弛效应. Zhang等[4]建立了考虑螺旋螺纹的螺栓连接板结构三维有限元模型,研究了其在轴向张力作用下沿啮合螺纹的载荷传递行为. 由于高保真模型建模复杂、耗时长,分析过程比较缓慢,尤其在进行螺栓连接结构的动力学研究时高保真模型更加难以适用,因此研究者们建立了螺栓连接结构的简化模型以提高模型计算效率. Luan等[5]用线性弹簧模拟螺栓连接法兰结合部接触界面,建立了简化的螺栓连接法兰结构动力学模型,并结合物理实验讨论了结构纵向振动频率与横向振动频率的关系. Meisami等[6]将螺栓法兰结构的结合部和螺栓分别视为悬臂梁和弹簧,建立了一个能反映实际结合部行为的解析模型,得到了载荷与挠度之间的精确关系. Xiang等[7]提出了一种考虑孔间隙和摩擦效应的改进弹簧法,并基于弹簧法和有限元理论对七螺栓双搭接板进行建模,研究了板宽、板厚、螺栓间距和间隙对载荷分布的影响. Deaner等[8]利用弹簧单元、粘滞阻尼单元以及一个四参数的Iwan单元建立了螺栓连接的双梁结构模型,在一定的受力水平范围内准确的描述了结构的刚度及阻尼. 李玲等[9]将栓接结合部刚度等效为结合面刚度和螺栓刚度的串联,并利用ANSYS软件建立了栓接梁结构的有限元模型. 孙伟等[10]提出采用简化的Iwan模型模拟螺栓结合面之间的非线性动力学现象,从而建立了螺栓连接组合梁非线性解析模型.
除上述针对螺栓结合部简化建模的方法外,还有很多学者将螺栓接合部简化成一种虚拟材料,并基于此完成螺栓连接结构的建模与分析. 例如,Iranzad和Ahmadian[11]采用薄层虚拟弹塑性材料模拟螺栓连接梁结合部的接触界面,建立了完整的动力学模型,并利用试验数据对其参数进行了识别. Wang和Fan[12]将螺栓连接梁的连接界面简化为虚拟材料,建立了螺栓连接梁的有限元模型,采用刚度和阻尼随频率变化的子结构描述结合部非线性动力学行为. Zha等[13]提出将螺栓结合面接触部分用一种横观各向同性的虚拟材料模拟并以此建立螺栓连接板的有限元模型,并将求解得到的模型固有频率和振型与实验结果进行比较,验证了模型的正确性. Yang等[14]提出了一种基于分形理论的虚拟材料模型并将其用于预测碳纤维增强塑料复合材料螺栓连接的固有频率.Shi和Zhang[15]提出了一种基于虚拟材料的栓接结合部界面参数化模型,在不同加载条件下对一个具有螺栓连接的力学结构进行了数值仿真. Ye等[16]利用螺栓结合部基本特征参数与材料应变能的关系推导出虚拟材料的参数,然后利用有限元分析软件建立了包含结合部的单螺栓连接内孔圆接头分析模型. Zhao等[17]提出了一种基于表面接触应力的非线性虚拟材料方法来描述螺栓连接,并以一个箱型螺栓连接结构模型为例进行了较精确的动态性能分析.
上述利用虚拟材料法建立的螺栓连接结构模型均与实验结果较为接近,但是上述模型中通常用赋以均匀参数的虚拟材料模拟螺栓结合面.事实上,真实螺栓结合部的接触面压力是非均匀分布的,而这种非均匀分布的接触面压力会影响到结构的振动特性. 因此,本文以螺栓连接薄板结构为研究对象,采用复模量非均匀分布的虚拟材料模拟螺栓连接结构的搭接部分,建立螺栓连接板的半解析模型. 文中具体介绍了建模思想及原理,给出了基于遗传算法反推虚拟材料各参数的辨识流程,并创新性地给出了求解频响函数的公式. 最后,以一个具体的螺栓连接薄板结构为例进行了实例研究,通过模型与物理实验结果间的对比验证了上述建模思想及方法的正确性和合理性.
1 基于虚拟材料复模量非均匀分布的螺栓搭接部分建模理念
1.1 建模理念
螺栓连接薄板结构由两块薄板搭接并由若干螺栓紧固在一起,本文考虑将搭接部分用虚拟材料进行模拟,在建模时将结构划分为板1、搭接部分及板2三个部分,并分别建模,如图1(a)所示.而为了更好地模拟搭接部分的力学特性,这里假设虚拟材料的储能模量分别服从线性分布、抛物线分布、正弦分布等非均匀分布形式,如图1(b)所示. 所研究的螺栓连接薄板结构,长度为l,宽度为,搭接部分长度为 l2-l1,宽度为,未搭接部分厚度为,搭接部分厚度为.

图1 虚拟材料储能模量非均匀分布. (a)三维结构示意;(b)二维结构示意Fig.1 Nonuniform distribution of the storage modulus of a virtual material: (a) 3D structure diagram; (b) 2D structure diagram
在本文的建模方法中,将虚拟材料的材料参数用复模量表示,具体为

首先确定搭接部分具体的储能模量分布. 基于图1中所描述的搭接部分储能模量以线性、抛物线、正弦分布的假定,搭接部分任意位置处的储能模量求解式可分别确定如下:

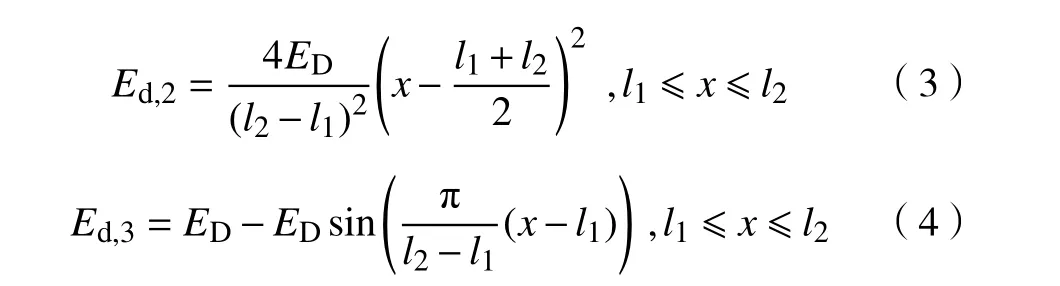
接下来确定搭接部分的耗能模量分布. 考虑到真实的螺栓结合部阻尼作用机理的复杂性,为简化建模,这里将搭接部分的耗能模量视为均匀分布,即搭接部分任意位置处的耗能模量均取值为.
1.2 虚拟材料储能模量与耗能模量参数确定方法
在上述的建模方法中,需要确定任意位置处的虚拟材料复模量值,其中储能模量已经给出了特定分布,故只需确定该分布下的最大储能模量值即可,而本文虚拟材料的耗能模量为均匀分布,即只需确定参数的值.
本文采用反推辨识法[18-19]识别上述待定参数及,将待定参数定义为设计变量,通过匹配计算不断对设计变量进行修正,使计算得到的结构振动特性与实验结果逐渐趋于一致,最终反推出待识别参数. 虚拟材料的储能模量直接影响到螺栓连接结构的固有频率,而其耗能模量直接影响螺栓连接结构的频响函数幅值,因而本文通过实际测试螺栓连接结构的固有频率和频响函数幅值来反推虚拟材料的储能模量与耗能模量.
图2为反推辨识虚拟材料储能模量和耗能模量的流程图,主要包括三部分内容:实验测试,通过锤击试验获取螺栓连接结构的各阶固有频率和频响函数;理论计算,利用自编半解析程序建立螺栓连接结构半解析模型,详情见第2部分;匹配计算,建立模型计算结果与实验测试结果的匹配关系,这里采用遗传算法[20-22]进行参数寻优,迭代计算辨识待定参数.

图2 虚拟材料储能模量(耗能模量)辨识流程Fig.2 Identification process of the storage modulus (loss modulus) of the virtual material
反推辨识虚拟材料储能模量的目标函数可表示为
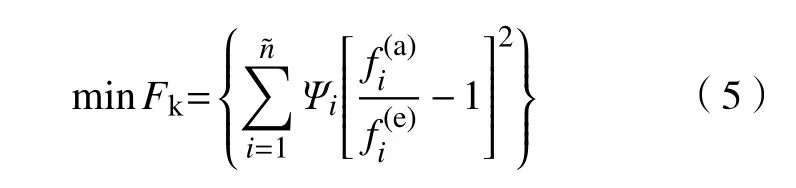
反推辨识虚拟材料耗能模量的目标函数可定义为
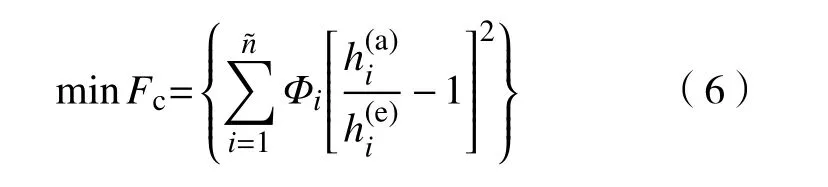
在算法中设定好目标函数的权重后,还需设定好算法中的种群数量(即每次迭代中给出的待辨识参数的数量)、变异概率(即种群中待辨识参数发生变异行为的概率)、交叉概率(即种群中待辨识参数发生交叉行为的概率),本文设定收敛条件为达到最大的迭代次数,通过若干次迭代发现目标结果已达到稳定值,由此输出辨识的待定参数,即获得辨识之后的虚拟材料储能模量及耗能模量参数.
2 螺栓连接薄板结构半解析建模及分析
2.1 搭接薄板结构能量方程的推导
上文建模理念中,将螺栓连接薄板结构划分为三部分(板1、搭接部分和板2),因其均属于薄板结构,故基于Kirchhoff假设和经典薄板理论,将整个结构的位移场[23-24]表示为
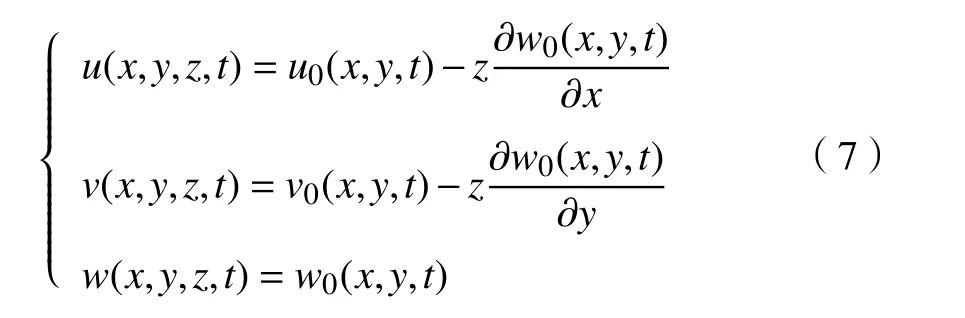
结构任意一点的应变可以用位移表示为

模型的应变能可表示为


2.2 螺栓连接薄板结构振动特性求解
假设自由状态下螺栓连接薄板结构中面横向位移 w0(x,y,t)做简谐运动,可表示为


3 实例研究
3.1 问题描述
这部分以螺栓连接钢板为例,描述本文提出的用复模量非均匀变化的虚拟材料模拟搭接部分的力学特性,进而完成整个结构的动力学建模与分析的方法. 图3为所研究的螺栓连接薄板结构,其由两块钢板经两个M6外六角头螺栓紧固连接构成,与所建半解析模型边界条件一致,其一端固定支撑在实验台上,相关几何及材料参数见表1.

图3 螺栓连接薄板结构实物图Fig.3 Real structure of the bolted thin-plate structure

表1 螺栓连接薄板结构中板的相关材料及几何参数Table 1 Material and geometric parameters of the plate in a bolted thin plate structure
螺栓预紧力影响着结合部的物理属性,预紧力的变化会对结合部的刚度和阻尼产生影响,进而会使得螺栓连接结构的固有特性产生一定变化,本文重点描述建模方法,因而仅以一个定常预紧力为例做研究. 对每个螺栓均施加3 N·m的预紧力,采用锤击法对该螺栓连接薄板结构进行固有特性测试,测试中通过PCB SN 30272力锤对薄板连接结构施加宽频激励,使用Polytec PDV-100激光多普勒测振仪拾振,LMS SCSDAS数据采集分析仪用于获取激励及响应信号,最终由获取的频响函数获得固有频率及模态振型. 实验过程中,拾振点如图3所示不变,在获取模态振型时,锤击点为图3中标注的所有节点,而图中突出标注的是下文所选取的频响函数在实验获取时的对应锤击点. 相关测试结果列在后续的与理论分析相对照的各图表中.
3.2 螺栓连接薄板结构半解析建模
两块连接薄板的搭接部分长为60 mm,宽为120 mm,按照式(2)~(4),依次给与搭接部分复模量以线性、抛物线、正弦分布,建立三种非均匀分布下的螺栓连接薄板结构半解析模型. 为了明确用哪种分布形式更能提升分析模型的精度,在这里进行了对比研究. 同时为了体现这种虚拟材料复模量非均匀分布建模理念的先进性,还对比了虚拟材料复模量均匀分布建模力学特性的结果.分别采用反推辨识技术,利用实测的前5阶固有频率,针对不同的虚拟材料复模量非均匀分布建模方式,确定虚拟材料的最大储能模量,其中对前5阶分配的权重依次为0.3、0.2、0.3、0.1、0.1,遗传算法中种群数量、变异概率、交叉概率、迭代次数依次设置为50、0.05、0.9和50,相关辨识结果见表2.
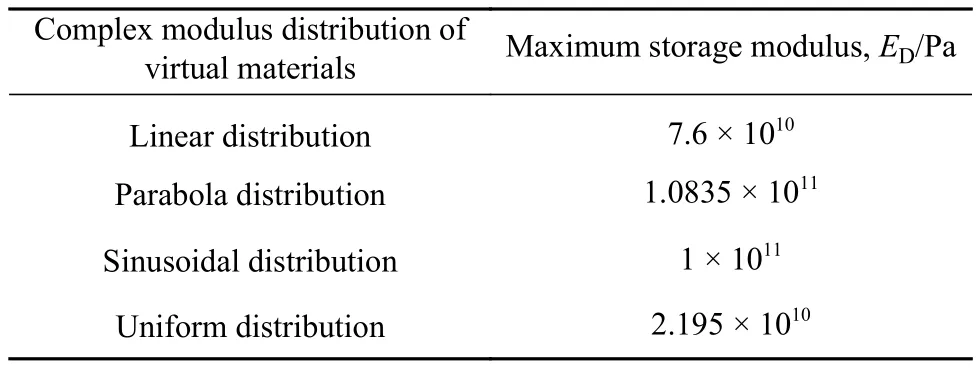
表2 反推法辨识获得的各分布状态下的虚拟材料储能模量Table 2 Storage modulus of the virtual material for each distribution obtained using the inverse identification technique
需要说明的是,表中的储能模量值是使对应分布下的模型达到最高模拟精度的量值. 用此储能模量值获得的螺栓连接薄板的前5阶固有频率与实验的比对分别见表3.

表3 各虚拟材料储能模量分布模型固有频率与实验固有频率对比Table 3 Comparison of the natural frequencies obtained using the virtual-material storage modulus distribution model and the experiment
由表3各数据间的对比可以非常直观的看出虚拟材料储能模量均匀分布时模型的固有频率与实验的接近程度明显差于虚拟材料储能模量非均匀分布时的结果. 进一步,利用均方根误差(RMSE)方法[26]对比上述三种非均匀分布模拟时的各阶固有频率与实验的偏差,将表3中的数据代入到式(24),获得对应三种分布形式的仿真与实验前5阶固有频率的RMSE,结果见表4.

表4 各非均匀分布形式中仿真与实验前5阶固有频率的均方根误差Table 4 Root mean square error (RMSE) of the first five natural experimental and simulated frequencies in various nonuniform distributions
通过表4中的RMSE对比可以看出,采用抛物线分布时,模型前5阶固有频率与实验的接近程度更好. 故在后续分析时,对于本文的结构,均采用虚拟材料储能模量按抛物线分布的模型进行模拟.
3.3 振动特性求解
前一部分已描述了固有频率的求解,这里继续求解螺栓连接板的模态振型. 仿真计算获得的模态振型与实测值的比对见表5,可以看出两者的振型基本一致.

表5 实验与仿真前5阶振型对照Table 5 Comparison of the first five experimental and simulated vibration modes
由于要确定虚拟材料的耗能模量,接下来进行模型频响函数的计算. 参照图3中描述的激励点和拾振点位置,利用式(23)进行频响函数的计算. 首先,利用反推辨识,对前5阶频响函数值依次分配 0.3、0.2、0.1、0.1、0.3的权重,设置种群数量、变异概率、交叉概率、迭代次数为50、0.05、0.9和50,不断迭代模型中虚拟材料的耗能模量值,使模型的频响函数曲线尽可能接近实测曲线,完成迭代后,虚拟材料的耗能模量为1.625×109Pa.接着用此耗能模量值获得最终的频响函数曲线并与实测比对,见图4. 从图中也可看出,仿真与实测的频响函数也有较好的接近.

图4 实测与仿真频响函数对比Fig.4 Comparison of the frequency response functions obtained based on the measured and simulated data
4 结论
(1)本文提出用复模量非均匀分布的虚拟材料来模拟螺栓搭接部分的刚度及阻尼特性,并给出详细的建模流程和方法. 实践表明本文采用假定的正弦、抛物线和线性等非均匀变化的虚拟材料模拟螺栓搭接部分,相比于均匀分布能够更加精确地模拟螺栓连接结构的动力学特性.
(2)采用虚拟材料模拟螺栓搭接部分,虚拟材料的材料参数用复模量表示,可直接生成复数形式的刚度矩阵,省却了常规建模中生成结合部阻尼矩阵的步骤,在保证模型精确性的基础上,简化了螺栓搭接部分的建模过程. 提出利用反推法辨识虚拟材料的储能模量和耗能模量,其中储能模量参数确定为其分布函数的最大值,耗能模量取相同值. 通过所提出的反推辨识流程可较为精确的确定虚拟材料的参数.
(3)为了更好地实施所研发的建模理念以及反推辨识确认虚拟材料的复模量参数,自行研发了半解析程序. 重点描述了复模量非均匀分布的虚拟材料引入螺栓连接结构半解析模型的过程,并推导出了快速求解半解析模型任意锤击点与拾振点处频响函数的公式. 最终的研究表明:用所创建的半解析模型计算获得的固有频率、模态振型以及频响函数值均与实验结果较为接近,从而证明了提出的用复模量非均匀分布的虚拟材料模拟螺栓影响区进而实施半解析建模可实现较高的仿真计算精度.
