基于模糊PID的变幅液压控制系统
2021-06-16陈志高胡仕成黎新齐
陈志高,胡仕成, 黎新齐
(1.中南大学 机电工程学院,湖南 长沙 410083;2.高性能复杂制造国家重点实验室,湖南 长沙 410083;3.山河智能技术中心,湖南 长沙 410100)
引言
高空带电机器人[1-2]是由机械臂、抓手、液压控制系统、车体所构成,抓手通过控制来完成自主识别导线位置,自动剥切导线绝缘层和支线线路与引线线路搭接等工作,因此保证抓手位置和操作的精确定位完全要依靠臂架的稳定控制,在其工作过程中,臂架不能出现振动抖动,要保证臂架相对稳定。
为了提高臂架液压控制的稳定性,对液压控制技术进行广泛研究[3-8],李阁强等[9]提出BP神经网络控制策略,设计了神经网络控制器,搭建模型并对其仿真,结果显示基于神经网络控制的闭环液压系统可以提高速度和压力的控制精度及稳定性能;李广等[10]采用非线性PID控制的方法,设计了非线性PID控制模型,通过跟踪器调节控制器参数,对液压缸活塞的速度进行了仿真验证,结果表明该控制方法可以提高液压系统的稳定性;石家庆等[11]提出了阀控缸液压系统在变负载下液压锁的一种模式,解决了系统振动抖动幅度较大的问题。
响应滞后时间、超调量、稳定时间是系统稳定性的反映指标,高空带电机器人是要保证抓手的工作精度,即工作时抓手可以精准的抓到主线完成线路维护检修任务,因此系统的超调量是优先需要满足的指标,必须尽可能降到最低。本研究设计了模糊PID控制器闭环液压控制系统来提高臂架的稳定性,不仅要满足超调量降低的要求,还要相对缩短系统的响应滞后时间和稳定时间,达到系统高精度、快响应的目标。以高空带电机器人的臂架变幅液压系统为研究对象,建立变幅液压系统液压缸的数学模型[12],设计模糊PID控制器,在MATLAB的Simulink环境下建立无PID、经典PID、模糊PID三种控制方案的仿真模型,最后通过搭建实验平台验证了所设计的模糊PID控制器的控制性能。
1 臂架系统总体设计
1.1 臂架三维模型
高空带电机器人主要包括臂架系统和液压控制系统,臂架系统包括底座、竖直臂、水平杆、伸缩杆、摆动杆、抓手。臂架液压控制系统主要由5大部分构成,分别为动力元件、执行元件、控制调节元件、辅助元件和工作介质,臂架系统如图1所示,具体杆件参数如表1所示,液压缸参数如表2所示。

1.旋转底座 2.竖直臂 3.连接杆 4.水平杆5.摆动杆 6.抓手图1 高空带电机器人三维模型

表1 臂架各杆件参数
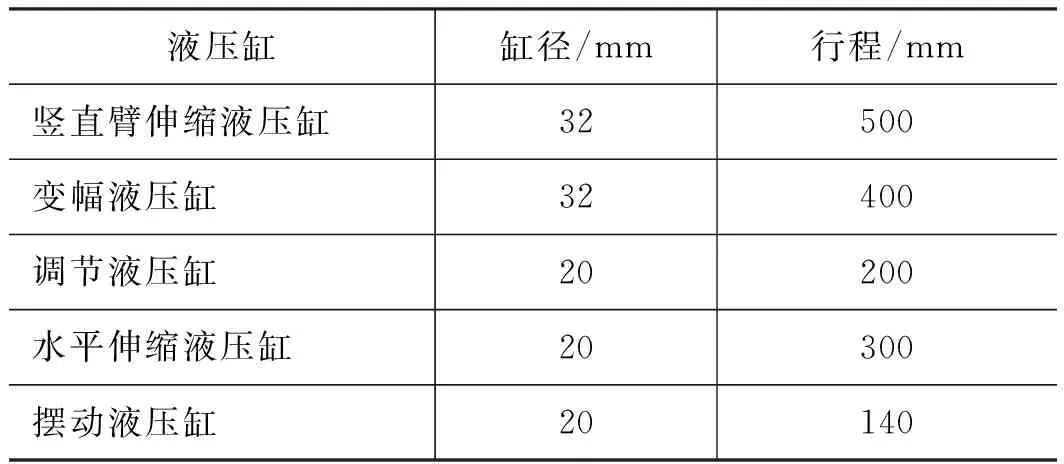
表2 臂架各液压缸参数
1.2 臂架的变幅液压控制系统
高空带电机器人通过远程控制臂架的液压系统来完成一系列高空带电工作,臂架的液压控制系统依靠顶升油缸、摆动油缸、变幅油缸的协调配合来实现,变幅液压控制系统原理图如图2所示,主要由液压泵、电液换向阀、平衡阀、变幅液压缸等组成。
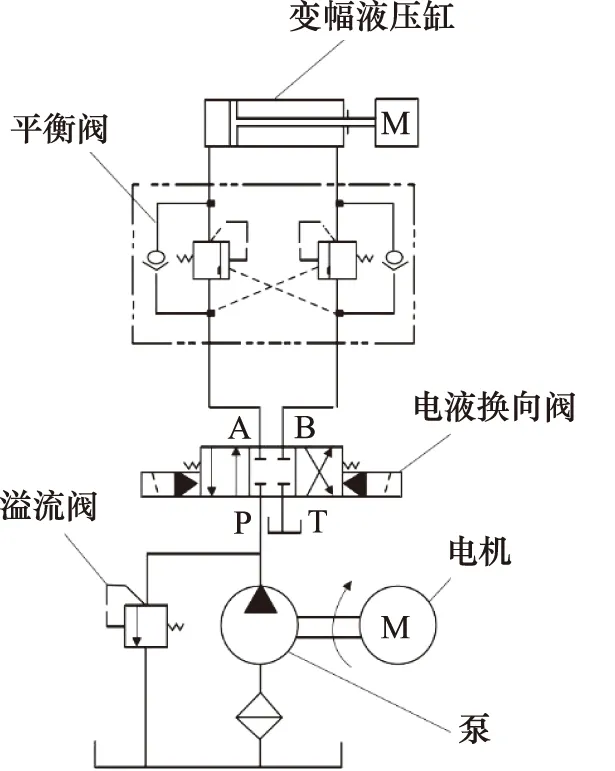
图2 变幅液压控制系统原理图
2 液压平衡回路数学模型的建立
液压平衡回路如图3所示,该回路液压缸力平衡方程为:

图3 液压缸平衡回路
(1)
式中,m—— 总质量
xp—— 活塞的位移
B—— 阻尼系数
FL—— 外负载力
Ff—— 摩擦力
pA—— 无杆腔压力
AA—— 无杆腔有效面积
pB—— 有杆腔压力
AB—— 有杆腔有效面积
拉普拉斯变换:
AApA(s)=MY(s)·s2+BY(s)+KY(s)
(2)
流量连续方程:
(3)
式中,np—— 电机转速
Dp—— 液压泵的排量
Cp—— 泄漏系数
pp—— 液压泵出口压力
VA0—— 无杆腔初始容积
βε—— 有效体积弹性模量
拉普拉斯变换得:
(4)
系统的传递函数为:
(5)
3 模糊控制器设计
3.1 模糊PID原理
自适应模糊PID控制器[13-14]以液压缸活塞杆的偏差e和偏差变化率ec作为输入,可以满足不同时刻的e和ec对PID参数自整定的要求。利用模糊控制规则在线对PID参数进行修改,便构成了自适应模糊PID控制器,其结构如图4所示。

图4 模糊PID控制器结构
图中r(t)是输入设定值函数,y(t)输出实际值函数,Δkp, Δki, Δkd为模糊输出变量。PID控制器的输入变量依据为:
Kp=Δkp+{e,ec}p
Ki=Δki+{e,ec}i
Kd=Δkd+{e,ec}d
其中,{e,ec}为不同时刻的偏差和偏差变化率对PID参数的调整函数。
3.2 模糊变量与模糊规则
设置e,ec,Δkp,Δki,Δkd的论域范围,输入变量e,ec设置为{NB,NM,NS,ZO,PS,PM,PB},模糊论域[15]均为{-3,-2,-1,0,1,2,3}。模糊推理后的输出变量Δkp,Δki,Δkd,采用增量形式,其变化范围:Δkp为[-1,1],Δki为[-10,10],Δkd为[-0.03,0.03],其中e,ec输出变量的隶属度函数设为7个,具体隶属度函数曲线如图5所示。

图5 各变量隶属度函数
模糊推理环节需要确定模糊控制规则,从系统的稳定性、响应速度、超调量和稳定精度等各方面来考虑模糊控制规则,模糊规则是根据当前时刻系统产生的误差,来制定的相应应对措施,确保系统各方面的性能。比例系数针对的是系统响应速度,积分系数针对的是系统稳态误差,微分系数针对的是系统动态特性,模糊规则表建立的依据如图6所示,Δkp,Δki,Δkd的具体模糊规则表见表3~表5。

图6 模糊规则表建立的依据
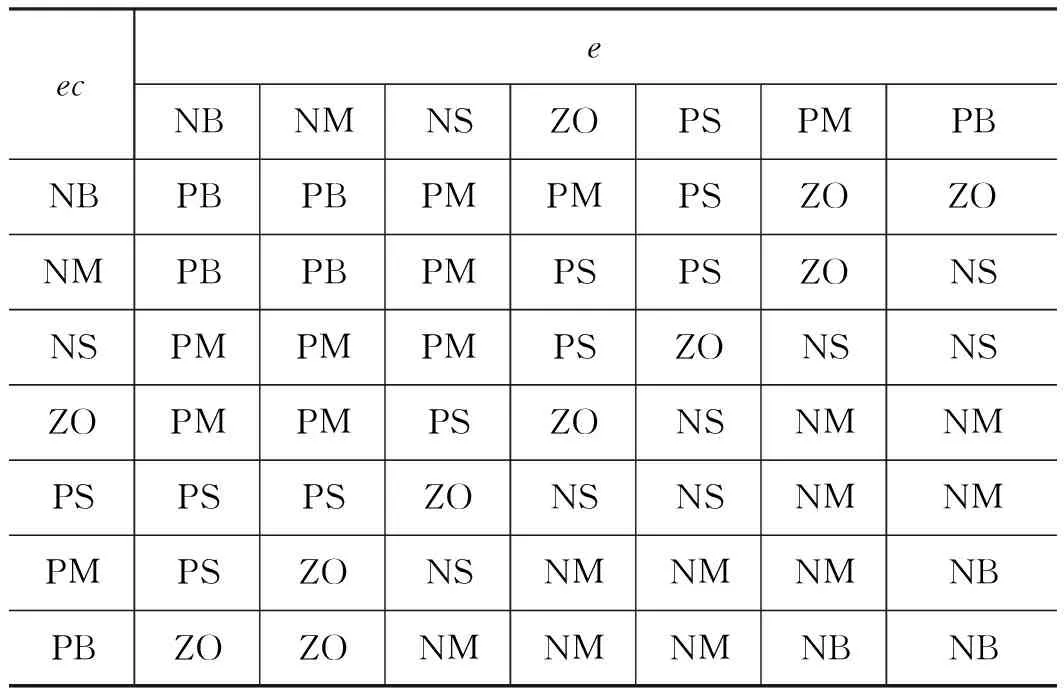
表3 Δkp的模糊规则表

表4 Δki的模糊规则表

表5 Δkd的模糊规则表
输出变量的模糊控制规则表建立好后,可根据以下流程来进行Δkp,Δki,Δkd的自适应校正,具体工作流程图如图7所示。

图7 工作流程图
4 MATLAB仿真分析
根据变幅液压控制系统模型,用MATLAB的Simulink进行建模仿真,模型为模糊PID控制、经典PID控制和无PID控制三种方案的比较仿真模型。建立的仿真模型图如图8所示。输入信号设为阶跃信号,所得到仿真结果如图9所示。

图8 3种方案的仿真模型
由图9可知,在第2秒时给变幅液压控制系统输入信号后,模糊PID相对于经典PID在响应时间、超调量、稳定时间上有较大改善。

图9 3种控制系统的仿真对比图
模糊PID控制的响应滞后时间最短为0.2 s,相对于经典PID的0.55 s,缩短了63.6%,超调量也大大降低,由PID控制系统的最大超调量0.09 m降到了0.01 m,超调量相对降低了88.9%,稳定时间也由PID控制系统的2.4 s缩短至0.4 s,相对降低了83.3%。
5 实验验证与结果分析
为了验证无PID控制、经典PID控制和模糊PID控制3种方案的实际控制效果,根据变幅液压控制系统的工作原理进行搭建实验平台[16],保证实验所添加的负载等外界条件与仿真的一致,按照仿真模型的思路进行逐一实验,并且给定相同的阶跃信号,所得到的实验结果数据如图10所示。
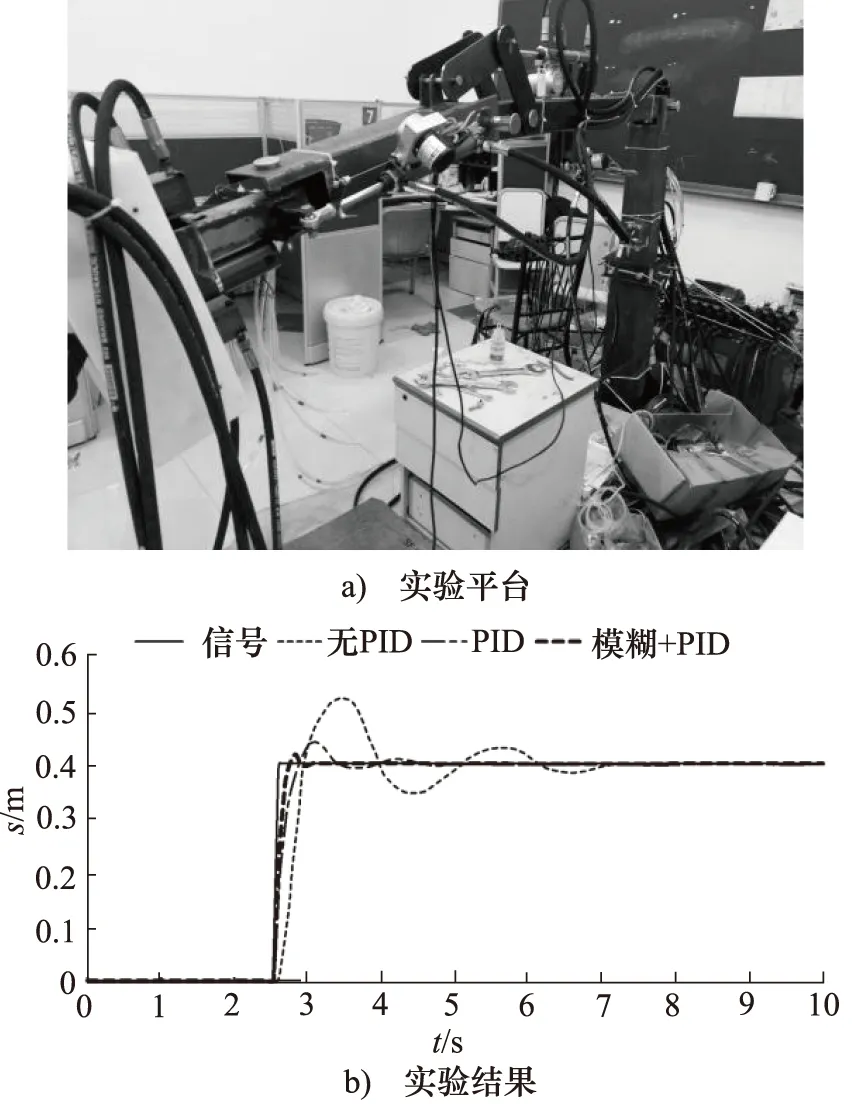
图10 3种方案实验图
由实验结果图可知,在2.5 s时给变幅液压系统输入阶跃信号后,三种系统控制方案的实验结果与仿真结果大体相近,并且从实验结果上可以看出模糊PID控制器在响应时间、超调量、稳定时间相较于无PID与经典PID都有较大的改善,模糊PID控制下的系统响应滞后时间相对于经典PID缩短了0.2 s,超调量降低了0.03 m,稳定时间缩短了1.7 s。
6 结论
(1) 本研究所设计的模糊PID控制器,在变幅液压控制系统中表现出来的控制性能优越,相较于经典PID有较明显的改进,能够大幅度的降低超调量和减少稳定时间,提高臂架的稳定性能;
(2) MATLAB仿真结果显示,模糊PID控制器相较于经典PID响应滞后时间缩短了63.6%,超调量相对降低了88.9%,稳定时间相对降低了83.3%;
(3) 实验结果显示,模糊PID控制下的系统响应滞后时间相对于经典PID缩短了0.2 s,超调量降低了0.03 m,稳定时间缩短了1.7 s。
