单桩式海洋风电装置风振数值分析和现场监测研究

李凯文,黄帅

(1. 广东电网能源发展有限公司,广东 广州 510160；2. 应急管理部国家自然灾害防治研究院,北京100085)

0 引言

随着风电装置大型化的发展,其结构的柔性也逐渐显著,由于空气动力、惯性力和弹性力等交变荷载的作用产生振动或变形,尤其是基础冲刷将会对结构动力特性产生显著影响,影响系统运行的可靠性,甚至会导致风电机整体倒塌,造成巨大的经济损失。国内外学者已经展开相关研究,但现场测试环境与条件相对恶劣,海上风大浪急,现场监测具有局限性[1—2]。现有研究主要集中在针对风电机结构数值进行仿真模拟,文献[3]分析了风浪对海上风电机动力特性的影响；文献[4]对p-y曲线法在海上单桩基础风电机的适用性进行了修正；文献[5]利用Fluent软件对风电机叶轮的气动性能进行了数值仿真研究；文献[6]根据现场监测数据对p-y曲线法在海上单桩基础在动力作用下的适用性进行了研究；文献[7]利用ANSYS建立了风电机塔架模型,对其固有频率和振型进行了研究；文献[8]对风电机叶片的流固耦合效应进行了分析；文献[9]对风电机叶片进行考虑流固耦合的数值模拟,分析了叶片与流场的相互作用对叶片和结构特性的影响；文献[10]研究了风场模型中强耦合算法与弱耦合算法的区别；文献[11]对大型海上单桩基础风电机桩土相互作用数值模拟进行了研究；文献[12—13]研究建模参数变化对风电机结构动力特性的影响。

综上所述,尽管对风电装置结构数值模拟及其数值方法研究方面取得了阶段性的成果,但以往研究主要是对单叶片或是基础的分析,未将风电机整机的风振反应纳入探讨。文中针对实际风电机的结构特点,建立了“风轮-机舱-塔架-基础”耦合的整机模型,并与现场监测数据进行对比分析,验证了精细化模拟的准确性。

1 风电机塔架振动现场监测

1.1 工程概况

现场监测的风电机组位于某海洋风电场,选取其中的单个风电装置为监测对象,该风电装置装机容量3.0 MW,轮毂高度86 m,塔架高度75 m,塔筒底部直径4.5 m,壁厚50 mm,塔筒顶部直径3.07 mm,壁厚20 mm,塔筒材料采用Q345；叶轮为三叶片形式,直径110 m；机舱罩为矩形结构,尺寸为12.9 m×5.0 m×5.9 m；风电机切入风速3.0 m/s,切出风速25 m/s。采用单桩式钢管基础,桩径5.0 m,桩长43 m,壁厚60 mm,桩基材料采用Q345。工程场地土的类型属于中软场地土,沿桩身方向向下,土层类型分别为粉砂层1、粉土层、粉砂层2、层状粉土层、粉质黏土层以及粉细砂层。各土层物理力学性能指标见表1。

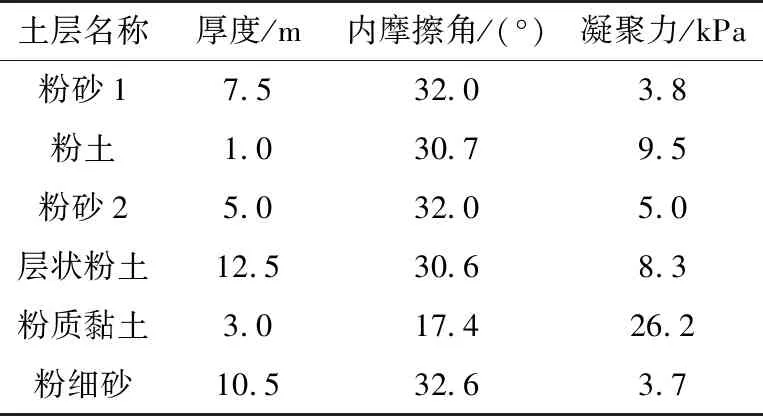
表1 土层物理力学性能指标Table 1 Physical and mechanical performance index of soil

1.2 传感器布置方案

加速度监测点沿风电机塔架高度方向布设,各组测点对应布置在平台一至平台五处,在观测点处放置一个单向加速度传感器,利用动态信号处理系统记录强风荷载作用下加速度的变化情况[14]。测试项目为风电机塔架的水平向振动加速度。测点布置和监测设备连接如图1所示。

图1 现场监测点的布设Fig.1 The arrangement of sensors at the monitoring

1.3 自振频率的测试

固有频率是反映结构动力特性的重要参数,现场监测中采用急刹车试验来测定风电机系统的固有频率。对风电机进行急刹车试验,即当风电机叶轮转速减至3.0 r/min时,进行急停试验,测试可以得到各个测点加速度时程曲线[15],试验数据如图2所示。

图2 急刹车测试时塔架顶部测点的自功率谱Fig. 2 Torsional power spectrum curve on top of the tower at braking test

由图2可以看出,2次急刹车试验的监测结果基本相近,对2次试验所测频率取平均值,得到该风电机整机结构的基本自振频率为0.329 Hz,阻尼比为0.009 5。文中所研究的风电机叶轮的转速范围为6.5～13.2 r/min,则风轮旋转频率为0.108～0.22 Hz,风轮叶片通过频率为0.325～0.66 Hz,塔架的自振频率在叶轮频率和叶片的通过频率之间,属于柔性塔。流固耦合效应对柔性塔结构的影响较大,风电机运行时风轮振动易与结构共振引起异常振动。风电机运行时风轮振动的激励频率允许范围可以参照《海上风力发电机组认证规范》,根据式(1)进行计算。

(1)

式中：fR为激励频率,指正常运行范围内风轮的旋转频率或风轮叶片通过频率；f0,n为支撑结构的第n阶固有频率。

由式(1)可知,若风轮转速在6.5～6.9 r/min持续运行,风轮激励会引起与风电机整个系统的共振。因此,在风电机运行过程中,应对其运行状态进行实时监测,并控制风轮旋转频率靠近激励频率,防止风电机系统因共振而产生破坏。

2 流固耦合计算方法

2.1 流体力学运动方程

风电机塔架结构流固耦合的区域可以描述为风压引起塔架结构的变形,而后者反过来影响风压分布。流体可以分为不可压缩流体和可压缩流体,而空气是最常见的不可压缩流体之一。三维不可压缩粘性流体的Navier-Stokes方程[13,16—17]为：

divu=0

(2)

(3)

式中：u为流体速度,u=(u1,u2,u3),其中u1,u2,u3分别为x,y,z方向上的速度分量；x1为体积上x方向,x2为体积上y方向,x3为体积上z方向；μ为流体动力粘度；p为流体压强；Fi为作用在流体区域上的体积力。

2.2 弹性结构体有限元方程

将结构划分为无限个单元,其中单个单元的运动方程可表述为：

(4)

结构整体的运行方程式可以根据单元的运动方程作为基础按一定方式叠加而得到：

(5)

2.3 流固耦合动力方程

在流固耦合计算中,分别定义风场模型和结构模型。结构模型基于Lagrangian坐标系,位移是基本未知量,而流体模型采用Arbitrary-Lagrangian-Eulerian坐标系,流体在力的作用下引起界面变形,并传递至结构引起结构的变形,通过流固耦合求解,可以计算出流场和结构场的应力应变、位移、加速度等,应用在流固耦合界面的基本条件是位移协调和力平衡,具体如下：

(6)

式中：uf为流体模型的位移；us为结构模型的位移；τf为流体模型的应力；τs为结构模型的应力。

根据力平衡条件,在流固耦合界面上,流体的分布力根据下式积分为集中力施加到相应的结构节点上：

(7)

式中：ud为结构节点的位移；S为流固耦合界面的面积。

流固耦合问题的物理实质就是联合求解方程组式(2)—式(4)和式(7)。

3 基于流固耦合的数值模拟方法

3.1 数值模型

将“风轮-机舱-塔架-桩基”作为整体来进行研究,并利用ADINA软件建立三维空间动力有限元模型。风轮为三叶片形式,采用3-D solid进行模拟；机舱由长方体在轮毂处切割一定倾角,采用3-D solid单元模拟；塔架采用壳体分段建立,单元划分采用9节点规则shell单元,网格密度采用定长值；桩基础采用beam单元模拟,桩土相互作用采用p-y曲线法[18]予以考虑,并在结构模型所有受风荷载的边界面上设定流固耦合边界条件,采用小变形假设,具体如表2所示。风场数值模型如图3所示。

表2 计算域的边界条件(缩尺比1∶1)Table 2 Boundary conditions with scale of 1∶1

图3 风电装置模型Fig.3 Model of the wind power installation

3.2 监测时的风速

现场风速可以通过风电机机舱顶部的测风系统进行实时记录,风速采集频率为10 Hz。现场测试随机风速情况如图4所示。

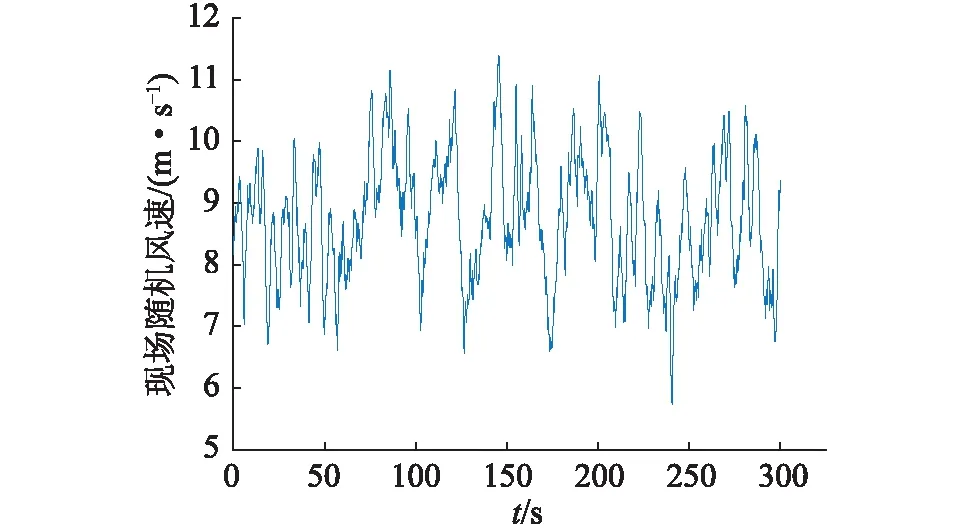
图4 监测现场随机风速Fig.4 Random velocity monitoring site

3.3 数值计算结果分析

文中采用有限元软件对风电机系统进行模态分析,风电机结构前4阶典型振型模态如图5所示。

图5 风电机前4阶模态振型Fig.5 The first four modal shapes and frequencies of typical wind turbine

由图5可知,风电机塔架的振动形式主要表现为侧向弯曲振动和实测得到的振动形式相同,考虑桩土相互作用时风电机塔架一阶频率0.320 Hz,实测值为0.329 Hz,通过比较可知,风电机塔架结构频率数值模拟值比实测值偏低,相差2.89%,从工程意义上来讲满足工程要求。

文中基于流固耦合理论,对在风速作用下,风场与结构的流固耦合作用进行了模拟分析,图6、图7为流场中典型的轴截面部分流速、湍流、流速以及气动压力云图。

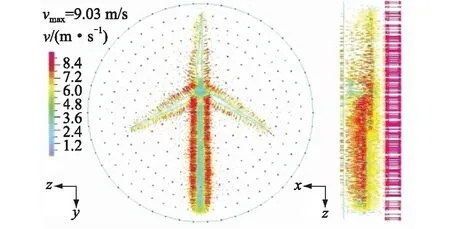
图6 风电机正面和侧面绝对速度矢量流场Fig.6 The front and side absolute flow velocity vector of wind turbines

图7 风电机正面和侧面流场压力分布Fig.7 Front and side pressure distribution of the flow field of wind

从图6可以看出,风场模型中,沿风电机流固耦合边界面处出现明显的速度集中区域,并在流固耦合边界面上流速方向改变,风速在不同程度上受到结构的阻碍作用。从图7可以看出,风电机流固耦合边界面上流场压力集中,区域外侧气体压强未受到扰动,风电机迎风面压力与背风面变化较大,说明文中提出的流固耦合的数值模拟方法能较好地反映风电机的流固耦合性质。此外,从图中可以明显地观测到风电机整机的气动特性和风速的流动现场,及其风速、流速等重要气动参数的分布特点,并能很好地显示出风电机周围的流场分布。

4 与现场监测结果对比分析

为了验证数值模型的合理性,在风电机塔架沿塔筒高度方向设置了多个测点,并计算了各个测点的振动情况,对比分析表明,不同测点的计算结果存在差异,但各测点结果的变化趋势相似。图8、图9比较了塔架不同高度位置测点塔门方向与塔门法向加速度值的现场监测结果和数值模拟结果。图中现场监测数据为塔门方向与塔门法向的加速度监测值,A5-2测点布设于塔架高度73.5 m处,A4-2测点布设于塔架高度44.8 m处,数值模拟中观测点对应于现场测试中的测点。

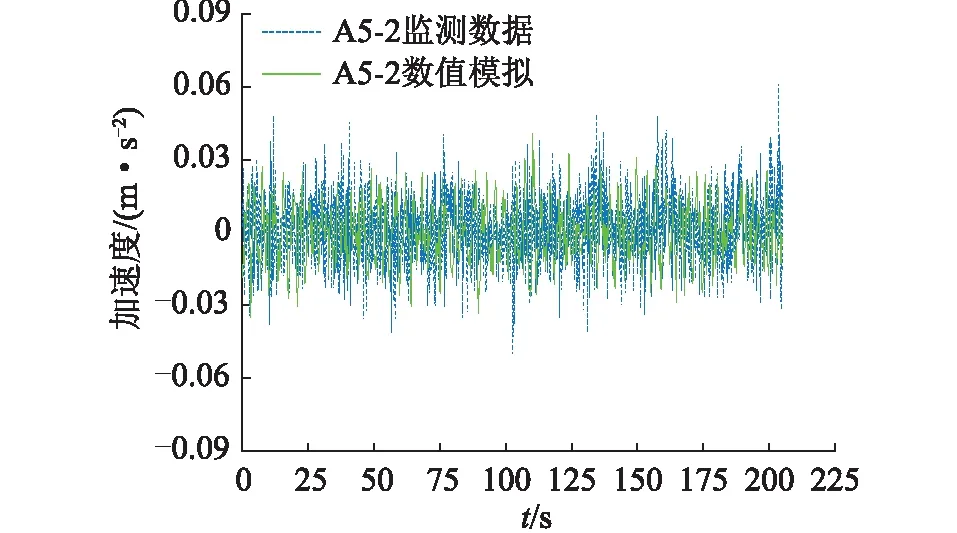
图8 塔架73.5 m处加速度模拟值与监测值Fig.8 Simulation and site monitoring values of acceleration at tower 73.5 m

图9 塔架44.8 m处加速度模拟值与监测值Fig.9 Simulation and site monitoring values of acceleration at tower 44.8 m

由图8可知,计算结果与实测结果在幅值和相位上存在一定的差异,分析认为这些差异是由于模型中约束及荷载边界条件与实际情况间的差异所致,但总体来说计算得到的结果同实测结果的变化趋势接近,表明文中模型较为合理,可用于大型风电机塔架结构风振反应分析中。

图10 比较了风电机塔架不同高度测点塔门方向和塔门法向加速度峰值的计算值与监测值。由于现场情况复杂,实测得到的各测点加速度峰值随风电机塔架高度不同而波动,但总的趋势仍然是逐渐增加,且与数值模拟相比,在峰值和递增规律上基本一致。

图10 塔架不同高度处加速度峰值模拟值与监测值Fig.10 Simulation and site monitoring values of peak acceleration at different tower heights

风电机塔架顶部塔门法向测点数值模拟结果为510 gal,与监测值相差17.3%,塔门方向观测点数值模拟值为1.7 gal,与监测值相差15%。虽然数值模拟值与监测值具有一定的差异,但是综合考虑数值模拟模型与实际模型存在一定的差异、实际风电机周边流场环境极为复杂以及监测本身也存在误差等情况,从工程应用研究的方面来说,是可以接受的。此外,从图中还可以看出,随着塔架高度的增加,塔架的直径与壁厚的变化会对塔架的动力响应产生影响。因此,在风电机塔架的加速度分析中,不能简单地乘以一个相同系数来处理不同高度加速度变化量。

5 结论

文中通过对风电机塔架进行现场监测与数值模拟对比分析可以得到以下结论：

(1) 通过现场监测测得了风电机整机系统基本振动频率,该频率与风轮振动的激励频率允许范围较为接近,容易引发风轮激励与塔架结构共振,因此在风电机运行中,须予以重视。

(2) 采用p-y曲线法模拟桩土相互作用,采用“风轮-机舱-塔架-基础”整机建模方法,并对其进行模态分析,分析结果与现场监测结果较为吻合,验证了整机建模的合理性。

(3) 考虑风荷载与风电机整机结构的流固耦合效应的动力响应分析,并与现场振动监测结果较为接近,从一定程度上说,采用数值风洞对风电机整机结构进行风振分析是可靠、可行的,可为风电机塔架风致振动的判别以及结构设计提供依据。

(4) 不同约束条件下风电机系统的固有频率不同,因此在风电机塔架结构施工中,可通过控制桩基础的约束程度来控制风电机塔架的固有频率,以避免风电机整机系统共振。