电化学储能参与电网低频第三道防线的控制策略
2021-06-16孙诚斌李兆伟李碧君邹燕周挺薛峰
孙诚斌,李兆伟,2,李碧君,邹燕,周挺,薛峰
(1. 南瑞集团(国网电力科学研究院)有限公司,江苏 南京 211106;2. 华北电力大学电气 与电子工程学院,北京 102206;3. 国网江苏省电力有限公司,江苏 南京 210024)
0 引言
目前,电化学储能(下文简称“储能”)已经成为新能源大规模接入和特高压直流建设的重要技术支撑,在电力系统中得到了广泛应用[1—4]。截至2020年6月底,我国储能的累计装机规模位列世界第二,为1 831.0 MW,同比增长53.9%[5]。
电网中故障引起的大容量功率缺额会造成系统频率下降,甚至引发频率崩溃,不断增加的新能源发电占比和高电压大容量输电恶化了电网频率的安全稳定[6]。低频减负荷是频率安全第三道防线的重要组成部分[7],可以快速响应有序切除部分负荷,防止频率进一步跌落。2019年英国“8·9”事件即是低频减负荷正确动作防止全网频率稳定破坏的典型案例[8]。但低频减负荷本身仍会造成大量用户失电,因此优化传统的频率校正控制策略,并将储能、直流等控制资源纳入其中,对提高电网应对极端严重故障的能力具有重要意义[9—13]。
储能系统具有响应速度快、有功/无功协调双向控制、功率转换效率高等特点,可以在电网频率偏移时快速调节其输出功率,改善电力系统的动态频率特性。随着储能电池性能的优化和成本的降低,将储能纳入电网频率安全防御体系中也更加具有研究价值[14—16]。文献[17]从频率安全角度出发,分析了储能在频率安全第三道防线里的作用及其容量配置的技术要点、储能技术未来的研究和应用方向;文献[18]提出了切机和储能协调实施紧急控制的思路,减少切机量和储能充放电次数。但如何制定储能参与频率安全第三道防线的控制策略,包括储能动作的频率阈值、分轮次功率调整容量等,现有文献中鲜有提及。
文中针对电网低频安全稳定问题,阐述了储能在电网低频第三道防线中的功能定位,提出储能参与校正控制的频率响应模型,并以频率恢复效果和控制代价为综合指标,提出适应多运行方式和故障场景的储能低频校正控制策略,最后在实际电网中对该方案的控制效果和适应性进行仿真验证。
1 储能参与频率安全第三道防线的定位和频率响应模型
储能参与电网频率安全第三道防线是指在电网频率大幅偏移的情况下,储能电站(单元)根据检测到的频率信号,转换充放电状态或调节输出功率大小,避免系统频率崩溃,主要用于应对诸如多台发电机跳闸、多回直流闭锁、稳定控制系统拒动等电网安全稳定第三级标准故障[19]。与低频提升直流、低频切泵等控制措施类似[20],是对传统低频切负荷、低频解列等频率校正控制措施的进一步扩展。
对于电网中广泛分布的分散式储能,采用就地分散校正控制可以降低通信成本和控制难度,提高系统可靠性。在低频第三道防线中加入储能不能替代现有低频减负荷的配置,而是为了利用储能调节灵活的优势,减少低频减负荷的动作风险,逐步优化第三道防线的配置容量和控制效果。为了提高电网应对极端故障的能力,同时降低低频减负荷动作风险,应单独设置用于低频校正控制的储能动作轮次。考虑储能动作代价以及直流功率支援对异步互联电网的影响,储能低频动作顺序应在直流功率调制之前,优先于低频切泵、低频减负荷的基本轮首轮次动作,并根据电网特性和储能可用容量确定频率级差和动作延时。
分析储能参与第三道防线对频率响应的影响,基于单机带集中负荷模型,含储能的转子运动方程为:
(1)

如果考虑负荷的频率特性,参与系统频率的调节,并且忽略负荷功率随母线电压变化,则负荷模型可简化为静态有功功率模型,负荷的有功功率-频率特性可表示为:
ΔPL=KLΔf
(2)
式中:ΔPL为负荷有功功率的变化量;Δf为频率偏差;KL为负荷的静态频率调节效应系数。
发电机组通过原动机的调速系统实现频率的有差调节,忽略原动机的再热时间常数,并考虑调速器响应时间,可用一阶惯性环节来表示发电机的功频调节特性[21]:
ΔPm=ΔfKG/(1+TGs)
(3)
式中:ΔPm为发电机的机械功率增量;KG为发电机的功频特性系数;TG为调速器时间常数;s为拉普拉斯算子。该式用来衡量在一定的频率偏差下,发电机机械功率出力变化的动态过程。
对于复杂的多机系统,发电机惯性时间常数可用加权平均法等值[22],如式(4)所示,调速器和负荷参数可基于遗传算法进行辨识等值[21]。
(4)
式中:SBi为第i台发电机的容量;HGi为第i台发电机的惯性时间常数;n为发电机数量。
在大功率扰动故障下,对于常规火电机组,电网运行准则要求其在频率变化时至少具备6%额定容量的调节能力[23]。由调速器模型可知,当系统频率偏差超过限值Δfm时,调速器的输入信号将达到限幅,而系统功率扰动越大,调门指令达到限幅的时间越短,即在大扰动故障下,可将调门指令等效为阶跃信号。
不同于储能参与一次调频,在储能的快速校正控制中,可以省去变流器的外环控制,忽略动态调节过程,在频率达到动作阈值时,储能的输出功率可快速调至给定值Ps[24]。忽略较小的时间常数和非线性部分,由此建立储能参与频率安全第三道防线的频率响应模型,具体如图1所示。

图1 储能参与频率安全第三道防线的频率响应模型Fig.1 Frequency response model of third defense lines containing energy storages
其中,ΔPe为系统的有功功率缺额,用阶跃响应表示,即ΔPe=Pe/s。若频率达到启动阈值的时间为te,经过延时td后储能调节输出功率,即ΔPs=Pse-tzs/s,tz=te+td。当Δf>Δfm时,调速器达到最大可调功率Pm,max。由图1可得功率发生缺额后系统频率响应的频域表达式,当Δf<Δfm时,调速器未达最大可调功率,有:
(5)
其中:
(6)
(7)
当Δf>Δfm时,用于一次调频的旋转备用满发,有:
(8)
经拉氏反变换可得频率时域表达式,Δf<Δfm时,频率响应表示为:
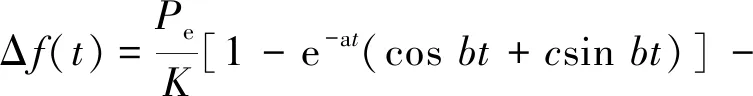
(9)
其中:
a=ξωn
(10)
(11)
(12)
K=KL+KG
(13)
当Δf>Δfm时,频率响应表达式为:
(14)
其中:
(15)
稳态频率偏差表示暂态过程结束后频率的恢复程度,由式(9)和式(14)可得稳态频率偏差表达式为:
(16)
储能系统在运行时,一般要考虑储能相关约束的限制。由于校正控制暂态时间尺度短,荷电状态几乎不变,因此在上述频率响应模型中可不考虑储能容量的约束。频率安全第三道防线需要能够应对电网中的各种不确定运行状态和随机扰动故障,并且其控制量无法精确统计,因此不考虑故障发生之前储能的充放电状态。考虑电网中所有储能全部参与校正控制,各轮次动作量按储能额定总容量的百分比进行调节(即控制量),减小储能运行状态对每轮次动作量的影响。
2 储能参与低频第三道防线的控制策略
储能参与低频校正控制的分轮次控制策略中,需要整定的参数主要包括:储能各轮次启动的频率阈值fe,k,各轮次功率的控制量和各轮次的动作延时td,k。综合考虑电网正常频率的运行范围及一次调频的运行要求,储能第一轮的动作阈值不宜高于49.5 Hz。当参与第三道防线的储能容量充足,需要设置多个储能低频动作轮次时,各轮次之间的频率级差可以按0.1~0.2 Hz确定,储能最终轮与低频减负荷第一轮的频率级差可以按0.1~0.2 Hz考虑。在实际工程应用中,各轮次的动作延时需要兼顾装置动作防误和频率控制效果两方面,一般设置为200~300 ms,可调整空间不大。
2.1 储能分轮次动作的临界容量
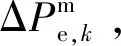
在发生大功率缺额扰动时,由式(16)可知,若第k轮不动作,则频率偏差达到Δfe,k对应的功率缺额为:
(17)
将频率由fe,k恢复到fsa的第k轮储能功率增量为:
(18)
目前储能在电网中的容量占比还相对较小,当达到储能低频动作阈值时,储能可快速投入最大功率,快速提供频率支撑。如果可用于校正控制的储能配置容量较大,则这种粗犷的控制策略可能造成电网发电功率过剩,导致频率高于正常水平,进而引发过频切机或新能源机组脱网等连锁事故。
由于电网运行方式具有复杂性和多变性,无法对所有的运行方式进行逐一计算,为了减少工作量,选取若干种典型的运行方式,如夏大、夏小、冬大、冬小等。通过对历年电网数据的分析,统计出电网各种运行方式累计运行时间、出现故障的类型及次数,得出概率分布情况,选取具有代表性的典型运行方式集C;在此基础上进行电网安全稳定分析,在安全稳定第三级标准故障中得出可能引起大功率缺额的大扰动故障集F。
根据式(17)和式(18),结合典型运行方式集C和扰动故障集F,筛选出造成功率缺额最小的运行方式和对应的扰动故障,代入频率响应模型,计算出满足电网频率过调约束的储能放电功率,其最大值即为储能分轮次参与低频安全第三道防线的临界容量Ps,b。当系统中可用于第三道防线的储能容量高于该值时,必须进行分轮次动作。
2.2 储能参与低频第三道防线的控制策略
在安排储能参与校正控制的策略时,根据电网的频率响应特性和已有的频率校正控制措施,整定频率阈值、延时和放电功率控制量。其中,储能低频动作的各轮次频率阈值应设定为不低于低频减负荷的首轮频率门槛值,使储能以更高的优先级参与到电网低频安全第三道防线中。若低频减负荷基本轮或特殊轮的频率作用范围和储能存在动作重合区,则必须考虑两者的协调:延时较短和控制代价较低的储能优先动作防止频率进一步降低,低频减负荷特殊轮动作防止频率在较低水平长时间悬浮;当储能全部轮次动作仍无法解决低频问题时,则由低频减负荷继续提供频率支撑。
确定了储能的频率阈值和延时后,对各轮次控制量进行整定和优化计算。储能的放电功率值逐轮次递增,各动作轮次整定量互相影响,决定了有功功率的支撑能力和频率的恢复效果。因此,为了制定控制效果最优的储能校正策略,必须综合考虑电网的运行方式、系统的功率不平衡量和各轮次动作量的情况,以储能轮次动作后的频率指标和控制代价为综合指标进行优化,确定在相关约束条件下各轮次储能的最优功率增量。由n个轮次储能功率增量表示的优化变量X为:
X=[ΔPds,1,ΔPds,2,…,ΔPds,n]
(19)
表征频率恢复效果和控制代价的综合指标为:
(20)
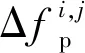
以上各系数的选取原则及其量纲的统一方法为:切负荷的控制代价要高于储能的控制代价,最低和最高频率指标的权重要高于稳态频率的权重;控制代价用各运行方式下储能动作量或切负荷量占额定储能容量或负荷功率的相对值表示(即控制量),频率指标用标幺值表示,以统一不同运行方式下的量纲。
构建考虑各种故障场景和运行方式的加权优化目标函数:
(21)
式中:λi为运行在方式i下的概率,μj为发生故障j的概率,均可根据历史数据统计得到;Nc为典型运行方式数;Nd为故障场景数。
综合储能的功率控制能力、电网频率、联络线功率的约束条件设定如下:
(22)
式中:Ps,max为储能系统最大放电功率值;最高和最低暂态频率的偏差值和也要满足一定约束,分别不能高于Δfd,max和Δfp,max,防止频率大幅度波动,避免一系列连锁故障[6];为了保障恢复效果,必须要求稳态频率在合理范围之内,Δfs,min和Δfs,max分别为稳态频率最小和最大值的偏差约束;同时,Ssec为断面的潮流约束,要满足联络线的最大送电能力Ssec,max的约束。
结合式(19)—式(22)的目标函数和约束条件,求解出最优储能放电功率增量ΔPds,k,并折算为占总装机容量Ps,N的比值ΔIs,k,得到各轮次储能的控制量:
(23)
综上,储能参与低频第三道防线控制方案的制定流程如图2所示。准备策略制定所需的数据,在典型运行方式集C和引起大功率缺额的大扰动故障集F下,建立计及储能参与频率安全第三道防线的频率响应模型,安排储能的动作轮数、各轮次启动的频率阈值和动作延时,优化储能各轮次控制量,得到储能低频校正控制方案,并校核校正控制动作后系统潮流的合理性。
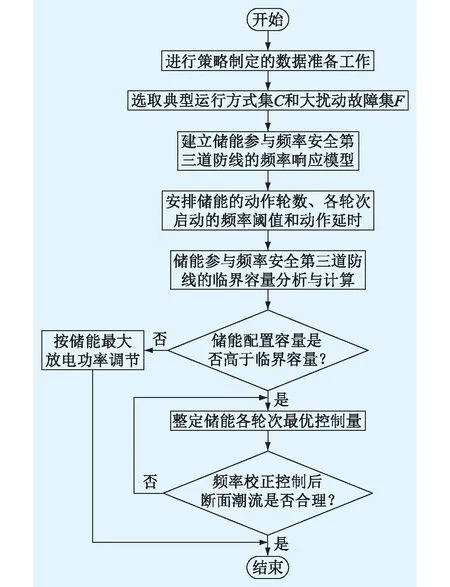
图2 最优控制方案的制定流程Fig.2 Tuning flowchart of the optimal control scheme
3 华东电网算例分析
在华东电网2个典型运行方式下进行仿真分析。华东电网的直流馈入示意如图3所示。
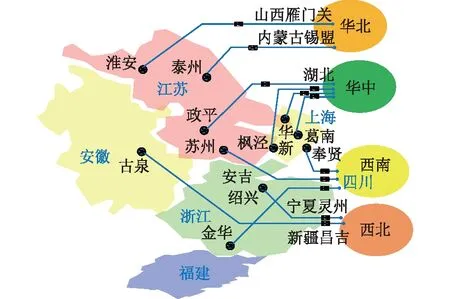
图3 华东电网直流馈入示意Fig.3 Schematic diagram of DC feed-in for East China Power Grid
方式Ⅰ总负荷功率为154 GW,总直流馈入功率为48.6 GW。方式Ⅱ总负荷功率为353 GW,总直流馈入功率为73 GW。低频减负荷的配置方案为:3轮基本轮和1轮特殊轮,在频率跌至49.0 Hz,48.75 Hz,48.5 Hz时分别切除负荷3.5%,4%和5.3%,并且频率低于49.0 Hz达到15 s以上时切除3%的负荷;2种方式下均配置了可用于校正控制的分散式储能,总计22.5 GW。典型故障场景由各直流的单/双极闭锁故障组成。经计算,方式Ⅰ和方式Ⅱ的临界储能容量分别为9.93 GW和14.4 GW。制定3种控制方案,其中方案1为储能不参与频率校正控制,结合电网频率特性,将储能轮次安排为3轮;方案2为按照文中方法得到的储能3个轮次控制方案;方案3为储能功率平均分配到3个轮次的控制方案,如表1所示。
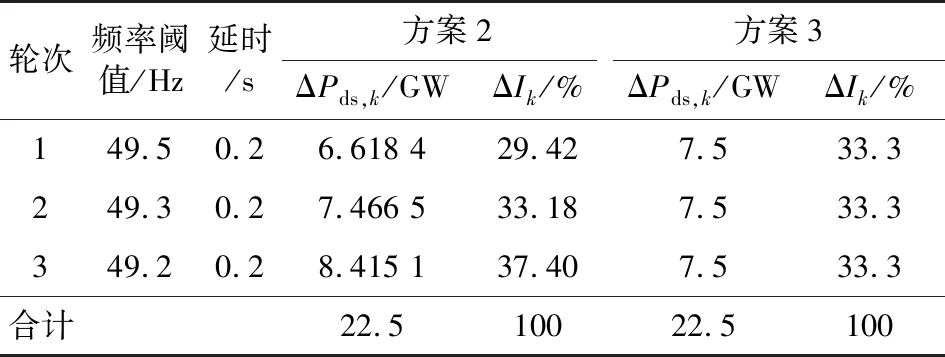
表1 储能参与低频第三道防线方案Table 1 Control schemes of third defense lines for low frequency containing energy storages
图4为2种运行方式下分别在0 s发生大功率缺额扰动a和b时,3个频率校正控制方案的频率响应曲线。

图4 不同控制方案下的频率曲线对比Fig.4 Comparison of frequency curves under different control schemes
其中,方式Ⅰ下发生故障a(锦苏、宾金直流双极闭锁,龙政直流单极闭锁),共造成功率缺额15.95 GW;方式Ⅱ下发生故障a,共造成功率缺额16.7 GW;方式Ⅱ下发生故障b(锦苏、宾金、复奉直流双极闭锁,雁淮直流单极闭锁),共造成功率缺额25.6 GW。可以看出,方案1中储能不参与控制,触发低频减负荷动作,或使频率悬浮于较低水平。而方案2和方案3均可以将频率恢复至额定值附近。
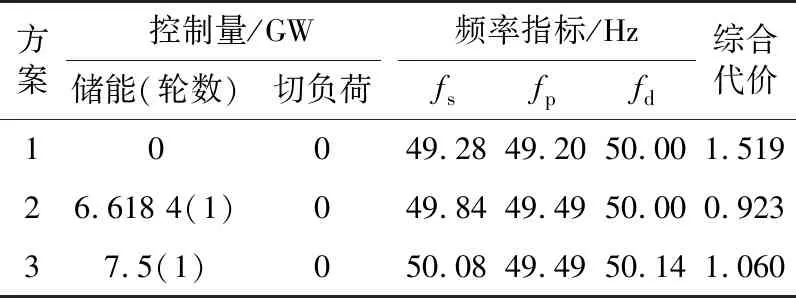
表2给出3种情况下不同控制方案的动作量、频率指标和综合指标。可以看出,方案2具有相较于其他方案更优的综合指标。方案1易触发低频减负荷动作,控制代价较大,且控制效果不佳,而方案3虽然可以避免切负荷,但在部分方式下会产生较大的频率过调,影响控制效果。因此,在结构较复杂和元件模型较多样的实际电网中,所述方法可以制定出较优的储能校正控制策略,解决各种运行方式下发生大功率缺额扰动后的低频问题,具有实际应用价值。

表2 控制量和频率指标的比较Table 2 Comparison of control quantity and frequency index(a) 方式 I 发生故障a
(b) 方式Ⅱ发生故障a
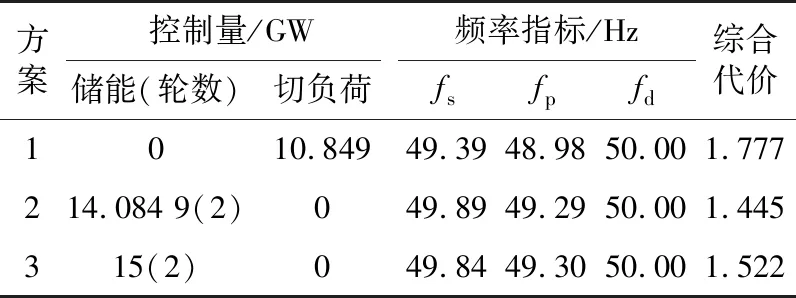
(c) 方式Ⅱ发生故障b
4 结语
新能源发电的快速发展和特高压直流的建设支撑了国家的能源转型战略实施,但也给电网的频率安全稳定控制带来了新的挑战。储能作为可以快速响应的有功控制资源,有利于提高电网的频率稳定水平,文中将其应用到低频第三道防线中,有如下结论:
(1) 分析了储能参与低频第三道防线的定位,将储能用于频率校正控制,可以充分利用储能的优势,既有利于电网的频率安全,也有助于提高储能的多重化利用效益。
(2) 考虑机组一次调频特性及负荷频率特性,建立了储能参与频率安全第三道防线的频率响应模型,有助于提高制定储能校正控制策略的工作效率。
(3) 提出了储能参与低频第三道防线的控制策略制定方法,综合考虑稳态频率、暂态频率以及控制代价,在保障频率安全的同时,降低低频减负荷动作风险。
将储能纳入到频率安全第三道防线依赖于储能的容量规模和运行状态,综合考虑储能多方面约束、协调储能在各种层面的控制,以及考虑频率安全风险的储能运行优化都有待进一步研究。
本文得到国网江苏省电力有限公司科技项目“大容量储能支撑机网安全稳定运行关键技术研究”(J2019027)资助,谨此致谢!
