独立轮电液伺服转向系统数学建模与验证

陈晖， 王涵， 杜恒， 张志忠

(福州大学机械工程及自动化学院， 流体动力与电液智能控制福建省高校重点实验室， 福建 福州 350108)

0 引言

汽车转向系统发展至今经历了机械式转向系统、 液压式助力转向系统、 电控电动式助力转向系统、 电控液压式助力转向系统等[1]. 对重型车辆助力转向系统而言， 传统的机械式全轮转向和液压式全轮转向系统无法同时满足多轴车辆灵活性和稳定性的要求， 而新型电控电动式转向系统功率密度小， 无法满足重型车辆负载大的要求[1]. 因此， 重型车辆的转向系统普遍采用电控液压式助力转向系统， 该转向系统同时满足重型车辆转向控制灵活性和高驱动能力的要求[2-4]. 传统的电液助力转向系统研究的大多是单自由度梯形机构， 这种转向系统通过横拉杆的作用实现双侧轮的同步转向. 但上述系统并不能满足重型车辆在蟹行、原地转向、 横移、 异向转向等极端工况下的转向要求. 相比较于传统转向系统， 独立轮转向系统具有更好的机动灵活性， 能使车辆满足更多的转向要求[5-7]. 所以， 为了改善重型车辆的转向性能特别是在极端工况下， 学者考虑将独立轮电液伺服转向系统应用于重型车辆.

建立准确的独立轮电液伺服转向系统数学模型是研究的关键一环, 由于实车测试的成本较高、 周期长, 易受空间天气影响. 为验证所建立模型的准确性， 搭建了与实车成1∶1比例的实验台架进行在环实验[8-10], 并且添加手动方向盘转角信号输入， 使其更接近实际转角工况. 该模型的验证成功对后续基于模型的非线性控制与分析研究提供了基础.

1 独立轮转向系统的理论建模

基于转向系统的机械结构建立拉格朗日动力学模型， 并以运动学关系以及液压系统建立数学模型，

再将数学模型转换为状态空间方程的形式.

1.1 机械结构的运动学和动力学建模

阀控单缸独立轮电液助力转向系统中的伺服比例阀直接控制一侧的单个非对称缸, 以实现单个车轮的独立转向. 由于转向系统为对称结构， 左、 右侧机构运动原理相同， 仅研究一侧转向系统即可清楚整个系统的特性. 以电液助力转向系统右侧结构为研究对象进行数学建模[11]. 车轴转向桥如图1所示.

图1 电液伺服转向运动结构和液压控制系统示意图(右侧转向)Fig.1 Schematic diagram of EHSS motion structure and hydraulic control system (right side)

设右侧车轮转角为β， 假设逆时针转向为正方向.系统的运动可简化为轮胎整体结构绕主销的转动， 其等效转动惯量为JR. 根据拉格朗日第二类方程建立单侧转向桥刚体约束动力学方程[12]， 如下式所示.

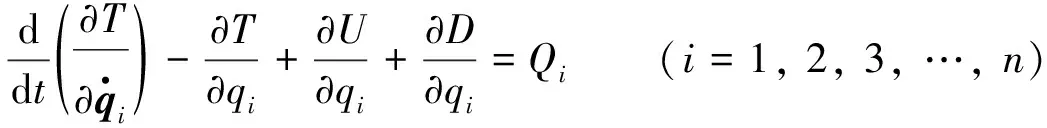
(1)

因考虑右侧的单缸转向， 系统的总动能即为右侧的转动动能. 除了轮胎整体结构的动能， 还存在势能和耗散能. 当小转向角产生弹性变形时， 势能表现为轮胎的弹性势能， 但由于建立轮胎弹性特性的分析模型较为困难， 直接将弹性势能部分纳入外负载的范畴来考虑. 因此以右侧车轮转角β为坐标， 有：

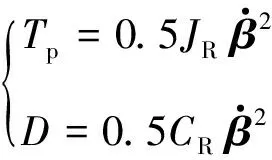
(2)

式中：JR为轮胎整体结构绕其主销转动的等效转动惯量;CR为轮胎整体结构的等效阻尼系数.

通过虚功原理和虚速度法， 可得广义力表达式：

(3)

式中：vR为转向节臂上转向助力缸驱动力作用点的速度；θ3为转向助力缸作用力与作用点速度的夹角；FR为助力缸的推力；TR为右轮转向阻力矩和.

如图1所示， 以上其他参数为：

(4)

式中：s30为s3的初始值.

式(3)中， 转向助力液压缸的输出力FR可表示为：

FR=p1RA-p2Ra

(5)

式中：p1R,p2R分别为右侧转向助力液压缸的无杆腔压力和有杆腔压力；A，a分别为右侧转向助力液压缸的无杆腔有效活塞面积和有杆腔有效活塞面积.

将式(2)～(5)代入拉格朗日方程(1)中， 即可得到阀控单缸电液助力转向系统转向运动的动力学方程：

(6)

1.2 电液伺服转向液压控制系统的数学建模

为实现独立轮转向系统中液压部分的控制， 需要对电液伺服转向液压控制系统进行数学建模， 建立伺服比例阀的阀口流量方程、 右侧转向助力缸的流量连续性方程. 忽略液压系统的一些次要因素， 进行如下假设：

1) 液压源是恒压源， 即ps为常数， 并且回油压力为零. 由于伺服比例阀到转向助力缸的油管较短， 其影响较小， 所以忽略管长的影响， 不考虑沿程损失， 不对其进行数学建模.

2) 伺服比例阀的阀口流量方程为：

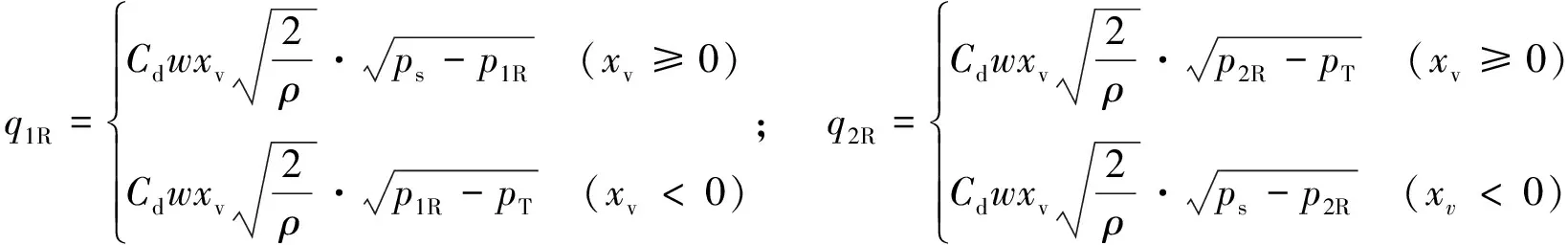
(7)

式中：Cd为伺服比例阀各节流口的流量系数；w为伺服比例阀各节流口的面积梯度；xv为伺服比例阀的开口量， 阀芯向左移为正方向；ρ为液压油的密度；ps为伺服比例阀P口的进油压力；pT为回油压力；p1,p2分别为伺服比例阀A口和B口的工作压力；q1,q2分别为流入和流出两转向助力缸的流量.

3) 助力缸的流量连续性方程：

(8)

式中：q1R,q2R分别为进入右侧转向助力缸无杆腔和有杆腔的流量；V1R,V2R分别为右侧转向助力缸无杆腔和有杆腔的容积.

其中，V1R和V2R满足关系式为：

V1R=V1R0+AxR;V2R=V2R0-axR

(9)

由式(4)可知：

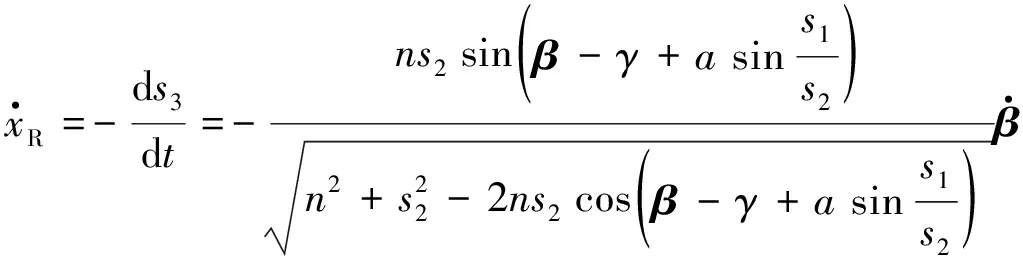
(10)

1.3 电液伺服转向液压控制系统的状态空间模型

为便于后续的研究及非线性控制方法的设计， 且状态空间模型可以更直观看出各变量之间的联系， 将所建立的数学模型转化为状态空间方程的形式. 定义状态变量， 输入和输出如下式所示：

(11)

从而获得转向系统状态空间表达式：

1.4 模型Simulink仿真验证

根据实际车辆工况以及实验器材(液压助力缸、 伺服比例阀、 液压油等)的具体参数， 转向系统的参数[1]设置如表1所示， 对模型进行初步仿真验证， 对所建立的状态空间模型(12)进行经典的PID控制， 在Simulink中进行仿真.

表1 转向系统的主要参数

在Simulink中搭建之前所建立的阀控单助力缸独立轮转向状态空间模型， 目标正弦信号空载后仿真结果如图2所示. 为了更贴近实际工况， 进一步引入2 t负载模型进行仿真验证[1]， 结果如图3所示.

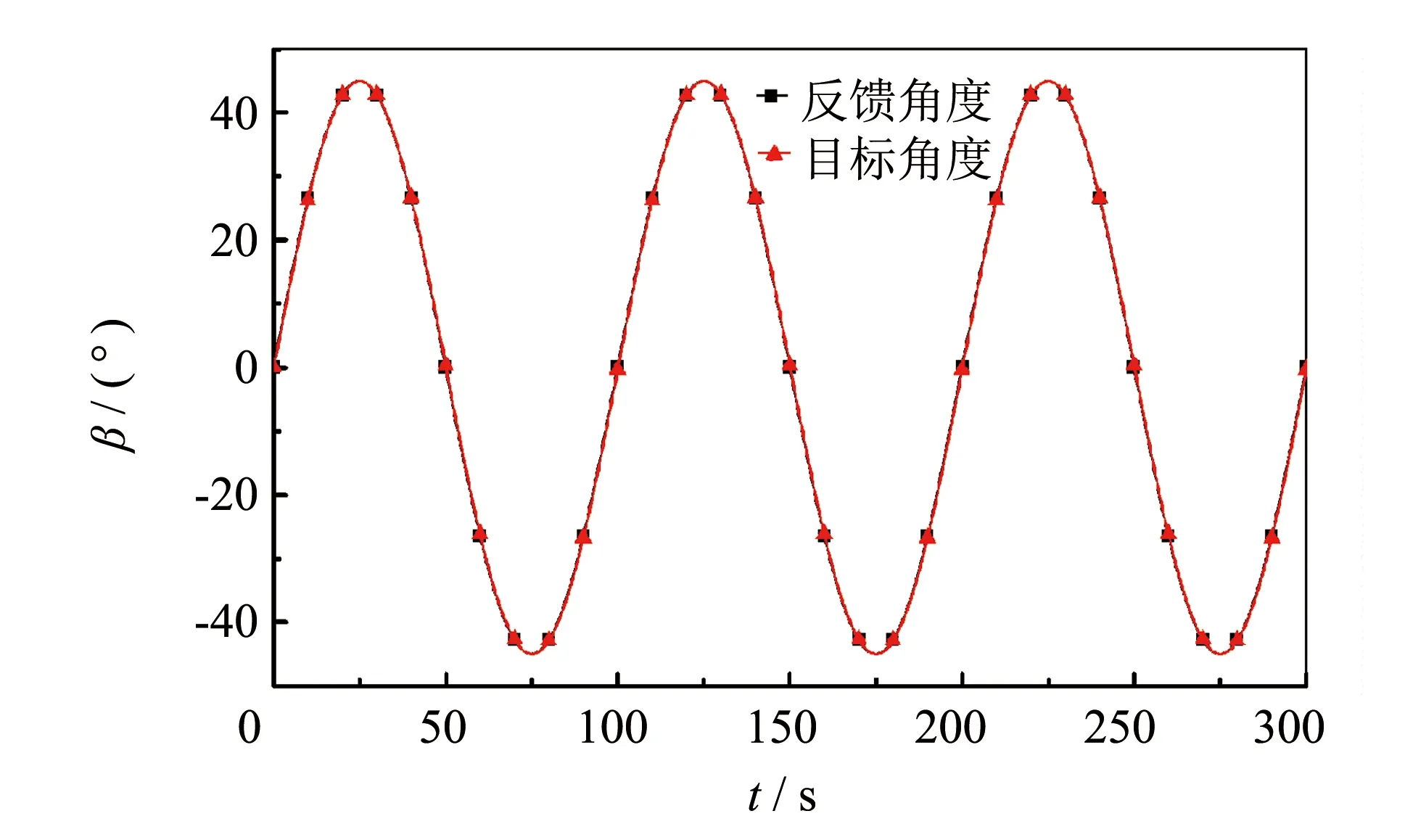
图2 PID控制策略跟踪效果Fig.2 PID controller tracking effect

图3 带载模型仿真跟踪效果Fig.3 Tracking effect of the loaded model

由以上仿真结果可以看出曲线跟踪良好， 误差约±1°， 满足控制要求. 因此, 可以进行模型验证实验的设计和操作.

2 阀控单缸独立轮模型实验验证

通过MLC控制器与dSPACE硬件， 设计单助力缸独立轮转向系统控制实验方案， 进行模型验证.

2.1 模型实验验证方案的设计

2.1.1 实验验证方案

为了验证所建模型的准确性， 需要对比实际物理模型与理论数学模型的跟踪效果和误差. 由于无法建立准确的阻力矩模型， 且为了减少扰动误差， 将模型和实验台架设为空载状态， 即轮胎悬空，TR=0. 利用dSPACE设备采集实时泵源压力并输入仿真模型内， 以接近实际波动泵源工况[13].

实验环境与流程如图4所示， 将目标转角信号同时输入MLC控制器和dSPACE设备， 以实现实际物理模型和理论数学模型的同步运行. 利用dSPACE ControlDesk软件同时监测台架和模型运行的反馈转角和压力与转角跟踪误差[13]， 对比验证仿真与实验反馈的跟踪角度和工作压力， 验证数学模型的准确性.

图4 实验环境与流程图Fig.4 Experimental environment and flow chart

2.1.2 实验参数确定

该系统由200 L·min-1变量泵提供动力. 由于其高响应性和可靠性， 采用力士乐MLC作为系统的控制器. 角度传感器用于采集安装在右轮上的实时角度信号. 供给压力、 有杆腔和无杆腔压力由3个压力传感器采集. dSPACE采集各个传感器的信号， 并实时监测转角、 压力和阀芯电压的信号. 其余模型仿真的各个参数与实验参数一致. 泵源压力取13 MPa， 控制器比例增益系数Kp=0.4.

由于系统转向过程中的阻尼力和惯性力无法建立准确的阻力矩模型， 且这部分对实验结果的影响不能忽略， 所以通过实验测得各种工况下转向助力缸两腔的压力. 经过计算得到空载状态下缸的推力， 拟合出轮胎整体结构的等效阻尼系数CR的范围为800～1 800， 且在此范围内的波动对仿真结果并无明显影响， 因此模型内的阻尼系数CR取1 000[14].

2.2 试验数据分析

为了模拟各种工况下的目标信号输入以更好地验证模型的准确性， 采用包括正弦信号和斜波信号在内的多种周期性固定信号输入， 以及模拟实际操纵情况， 通过方向盘进行手动信号的输入. 对比各种信号的跟踪效果.

2.2.1 固定信号输入分析

周期性固定信号的实验数据曲线如图5、 6所示. 由于系统的惯量大， 固有频率较低， 取正弦信号频率为0.1 Hz， 斜波信号的斜线斜率为±8 (°)·s-1. 实际工况如此大角度下， 频率0.1 Hz是非常快的， 且系统截止频率为1.13 Hz， 只有转向角度较小时才能达到如此高的频响[15]. 由图对比角度、 转角误差和工作压力的数据， 角度误差小于±2 (°)·s-1， 有杆腔和无杆腔的工作压力波动趋势和大小较为匹配. 因此可验证固定信号下所建模型的准确性.

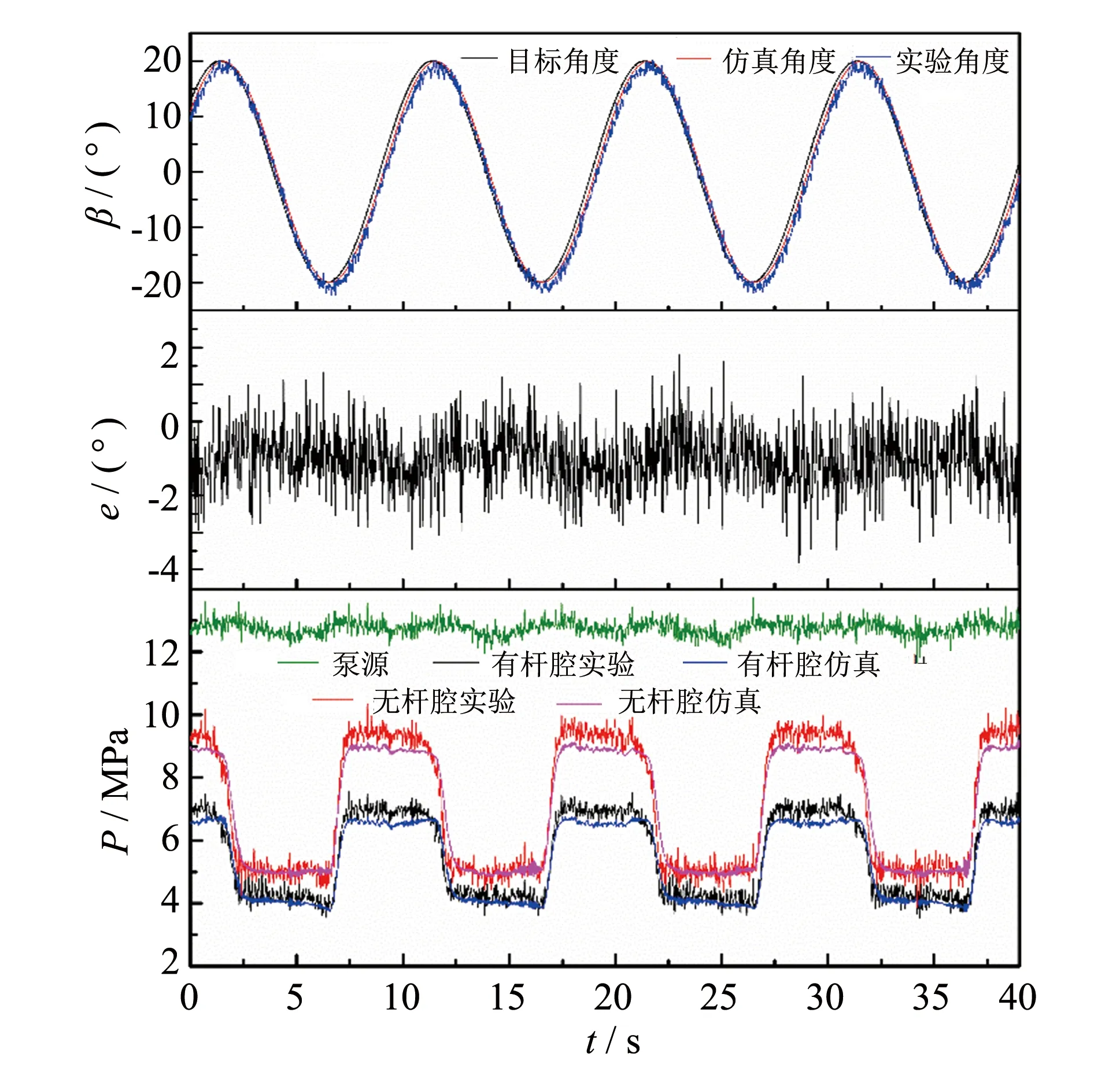
图5 正弦信号实验仿真对比Fig.5 Experimental simulation comparison of sinusoidal signals

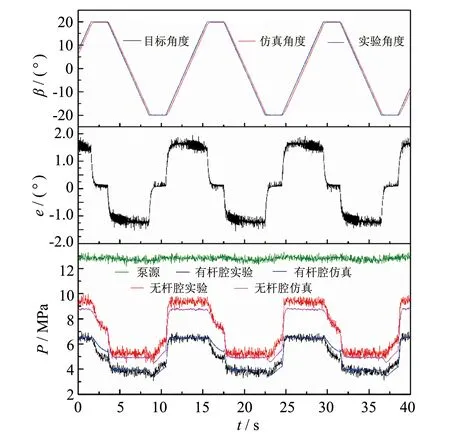
图6 斜波信号实验仿真对比Fig.6 Experimental simulation comparison of oblique wave signals

2.2.2 手动信号输入分析

手动输入角度跟踪曲线如图7、 8所示. 由图中可以看出， 系统可以进行良好的跟踪， 并且实验转角曲线和仿真转角曲线基本一致， 系统误差保持在-0.5°～1.5°以内. 可以得出实验曲线与仿真曲线不管是在数值还是变化趋势上都较为匹配.

图7 手动信号角度实验仿真对比Fig.7 Experimental simulation comparison of manual signals

图8 手动信号下角度误差Fig.8 Angle error of manual signals

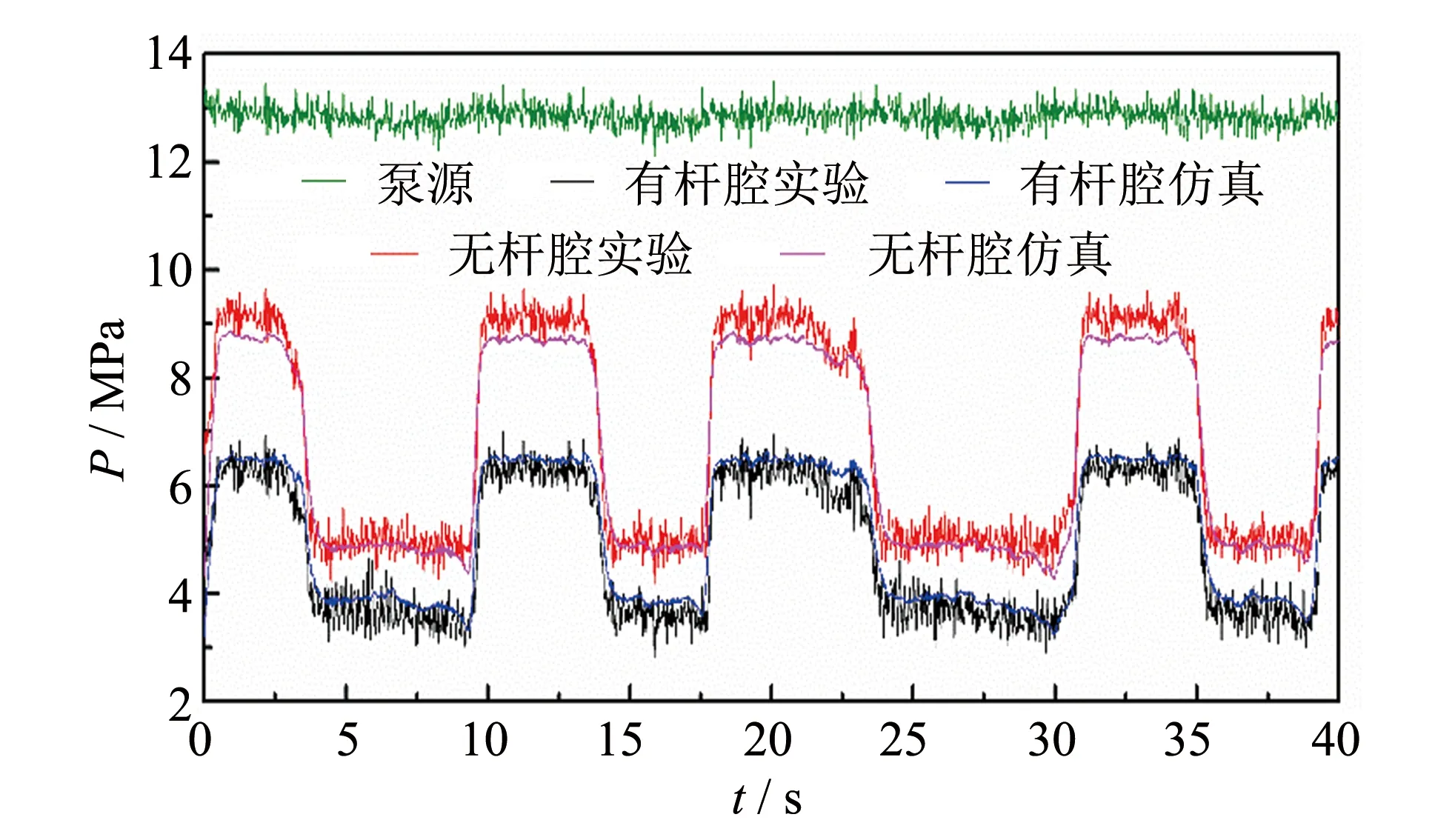
图9 手动输入信号下工作压力对比Fig.9 Working pressure comparison of manual signals

图9为伺服比例阀有杆腔和无杆腔仿真和实验的工作压力对比. 由图中可以看出其变化趋势和数值在阀处于工作状态时， 实验与仿真的结果基本一致. 由于实验采用的为非对称缸， 有杆腔面积小于无杆腔面积， 因此有杆腔压力大于无杆腔压力， 且有杆腔压力和无杆腔压力之和并不等于泵源压力.

从上述的分析可知， 在手动信号输入的状态下， 所建立的数学模型仍然能够较好地表达整个电液伺服转向系统， 证明了无论是手动随机信号输入还是各种固定信号输入， 各项状态数据曲线都基本匹配， 因此所建立的数学模型能很好地表达阀控单缸独立轮转向系统.

3 结语

基于拉格朗日动力学方程， 建立一种重型车辆阀控单缸独立轮电液助力转向数学模型， 并将其转化为状态空间模型. 同时搭建一套与实车转向系统1∶1比例的实验台架， 设计实验方案在各类输入信号下验证模型的准确性. 实验结果显示不同目标转角下角度跟踪误差在±2°以内， 有杆腔和无杆腔工作压力跟踪基本匹配， 表明本研究所建立独立轮电液伺服转向系统数学模型正确.

由于本研究所采用的控制器为PID控制， PID参数值越大时， 响应速度越快， 误差值越小， 但是增大到一定范围后实验抖动现象加重， 因此提高响应速度和减小误差需进一步研究非线性控制， 可为后续基于模型的非线性控制奠定基础.