公交乘客可靠度信号配时优化

赖元文， 马振鸿

(福州大学土木工程学院, 福建 福州 350108)

0 引言

交叉口作为城市交通系统的重要节点， 对于交通的疏解具有决定性作用， 而信号配时优化可以改善主要交叉口的运行状况[1]， 提升路网可靠性. 因此， 为了有效提升城市道路交通的运行效率， 使交叉口从堵点变成疏点， 有必要对交叉口配时优化和可靠性进行研究， 以最大限度提升交叉口可靠性， 提高交叉口使用效率.

现已有许多关于公交优先信号控制方面的研究， 如为公交车辆提供优先服务的双向行驶单车道[2]， 基于布朗运动的公交信号优先优化模型[3]， 针对过饱和信号交叉口提出的信号周期时长优化方法[4]， 分别以乘客、 车辆延误为优化目标的信号配时优化模型[5-6]， 考虑公交车和社会车差异建立的车道信号协同配置模型[7]， 以及基于相位清空可靠度建立的信号配时优化模型[8].

对于可靠性理论而言， 目前可靠性技术已在道路交通系统及公共交通系统中得到较多研究， 越来越多的交通问题研究引入可靠性理论. 如在公交服务可靠性上， 有公交服务可靠性测度指标模型[9]， 基于公交服务可靠性的公交到站时刻表编排模型[10]； 在道路连通可靠性上， 有道路连通可靠度模型[11]， 求解道路连通可靠度的递推分解算法[12]； 在道路通行能力可靠性上， 包丹文等[13]构建的城市组团运输通道可靠度测算模型， 以及研究快速路路段的通行能力可靠性评估方法[14]； 在行程时间可靠性上， 有评价公交行程时间可靠性的Mixed Logit模型[15]以及对公交行程时间可靠性影响因素的研究讨论等[16-18].

就交通问题的可靠性研究和信号配时优化研究而言， 现有的研究大多以车辆为研究对象， 从乘客角度研究的为数不多. 本研究从公交乘客角度出发， 引入公交乘客可靠度指标， 考虑公交车辆平均载客数分布性， 研究公交乘客可靠度与信号周期时长之间的关系， 推导得到给定公交乘客可靠度指标下的周期时长和绿灯时间的计算公式， 并与Webster信号配时方案对比， 通过仿真验证模型的有效性.

1 公交乘客可靠度模型

1.1 公交乘客可靠度定义

可靠度是在规定的条件和时间内， 完成规定功能的能力. 根据可靠度理论， 对公交乘客可靠度进行定义， 即在一定条件下， 相位i在绿灯时间内能够放行该周期内到达公交乘客的概率Bpi，Bpi可由下式表示.

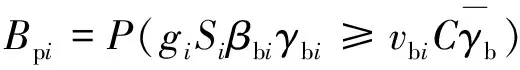
(1)

1.2 表征特征

公交车辆在交叉口运行情况最直观的表征指标是在规定绿灯时间内可以放行的车辆数量， 但是由于每辆公交车辆实际运载的乘客数存在差异. 因此对于公交乘客在交叉口疏散情况用绿灯时间内清空的公交车辆数表征则会存在一定偏差， 例如运载乘客数多的公交车辆未能通过交叉口， 而运载乘客数较少的公交车辆通过交叉口， 则该交叉口的公交乘客可靠度相对较低. 在实际情况下公交乘客可靠度越大， 说明交叉口放行的公交乘客越多， 也意味着公交乘客通过效率越大.

2 模型建立

2.1 计算模型

当公交车辆在站点完成停靠后， 其载客数不断变化. 对于有多个站点(包含首末站)的公交线路来说， 其载客数存在多种可能， 获取车辆实时载客数存在较大困难， 因此研究选取公交车辆平均载客数进行分布拟合.

2.1.1 公交车辆平均载客数分布拟合

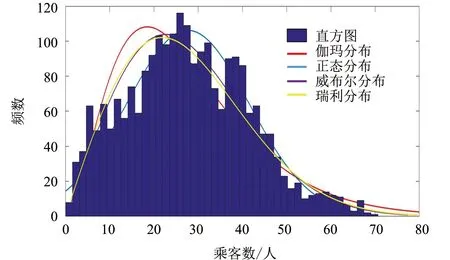
图1 公交车辆载客数分布拟合图 Fig.1 Fitting diagram of the distribution of the number of passengers on the bus

本研究利用福州市公交运营数据， 通过比选伽玛分布、 正态分布、 威布尔分布、 瑞利分布对公交车辆载客数的拟合效果， 确定拟合效果最好的概率分布.

具体步骤如下：

Step 1 剔除无效运营数据(如定制公交、 旅游专线等)， 计算公交车辆平均载客数， 通过频数和频率分析， 作直方图并初步分析公交车辆平均载客数的分布特征.

Step 2 对公交车辆平均载客数进行伽玛分布、 正态分布、 威布尔分布、 瑞利分布拟合， 如图1所示.

Step 3 计算出概率分布拟合的均方根(RMSE)和确定系数(R2)， 比选出优合度最髙的概率分布.

4种概率分布对公交车辆载客数的拟合优度对比见表1. 其中均方根RMSE是观测值和回归值误差平方和的均值的平方根， 如式(2)所示. RMSE的值越小， 说明模型选择和拟合更好. 确定系数R2是回归平方和(SSR)与总的变差平方和(SST)的比值， 如式(3)所示. 确定系数越接近1， 方程的解释能力越强， 模型对数据的拟合也越好.

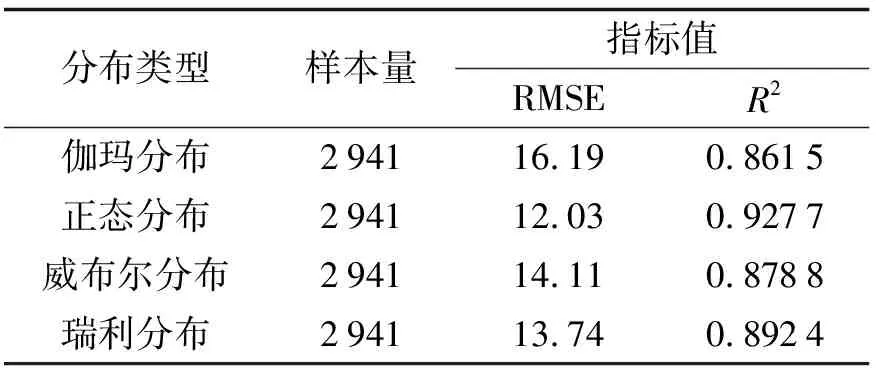
表1 各分布拟合对比

(2)

(3)

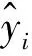
由表1可知， 正态分布对公交车辆平均载客数的拟合度是最好的.

根据福州市公交运营数据记录的客流量及运营班次， 可以得到公交车辆平均载客数， 部分公交运营数据如表2所示.

表2 2019年福州市96路公交运营数据(部分)

根据福州市2019年1月至9月的公交运营数据， 本研究确定公交车辆平均载客数为30人·辆-1.

2.2 模型表达

文献研究表明公交车到达率服从泊松分布[19]， 且具有不确定性. 通过对福州市公交车辆的到离站数据进行统计分析， 结果如图2所示， 金山明星站连续一周的到离站数据统计结果也证明了这一结论， 即公交车到达率具有不确定性.

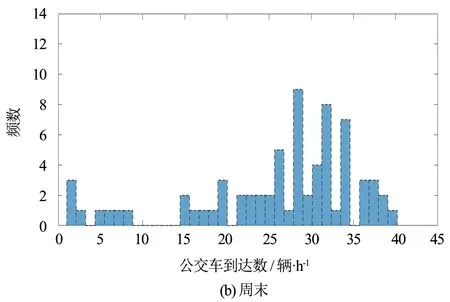
图2 金山明星站的到离站数据统计结果

(4)

根据标准正态分布表可知

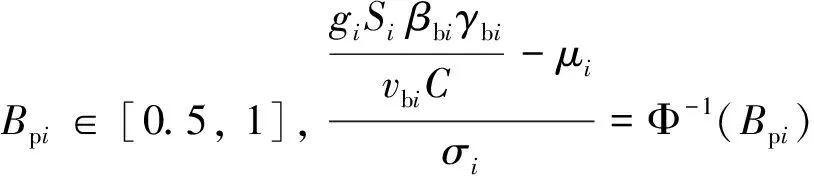
(5)

Bpi∈[0, 0.5], Φ-1(Bpi)=-Φ-1(1-Bpi)

(6)

于是可以得到

(7)

式中， Φ-1(Bpi)为标准正态分布函数Φ(Bpi)的反函数.

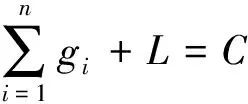
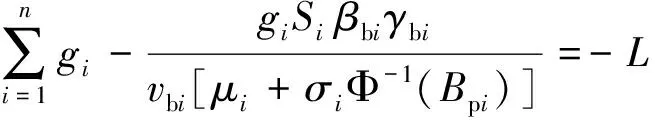
(8)

g1+g2+…+gi-1+gi(1-Ai)+gi+1+…+gn=-L

(9)

利用高斯消元法求解式(9)， 式(9)的增广矩阵为

(10)

对上述增广矩阵(10)进行初等变换， 得到如下矩阵

(11)

将矩阵(11)按第1行展开， 可得到式(9)的系数矩阵的行列式值D为

(12)

由Ai可知当βbi≠0， 即相位i有公交车辆到达时， 行列式值D≠0， 根据系数矩阵、 行列式值的定义可知式(9)有唯一解， 可得

(13)

3 案例分析

3.1 参数分析

设定某交叉口采用两相位信号控制方式， 且S1=S2=1 800辆·h-1， 信号总损失时间L=6 s， 分析周期时长与公交乘客可靠度之间的关系.

图3 不同公交车比例下周期与公交乘客可靠度之间的关系Fig.3 Relationship between cycle and bus passenger reliability under different bus ratios

假定两个相位的期望流量值都是1 000辆·h-1， 给定非公交优先方向的公交乘客可靠度为0.5， 即Bp2=0.5； 非公交优先方向的公交车比例为10%， 即βb2=10%. 公交优先方向的公交车比例分别为10%、 20%、 30%， 即βb1=10%、 20%、 30%. 分析公交优先方向不同公交车比例βb1及公交乘客可靠度Bp1对交叉口周期时长的影响， 结果如图3所示.

图3为信号周期时长与公交乘客可靠度在不同公交车比例下的变化趋势， 当Bp1从0.5增加到0.6时的信号周期增长速率比Bp1从0.8增加到0.9时快， 并且随着公交优先方向的公交车比例增加， 交叉口信号周期长度也随之增长. 总的来说， 增加Bp1的值会使信号周期时长增长， 一味地增加公交可靠度会使信号周期时长超出正常范围.

为研究公交乘客可靠度随非公交优先方向流量不同的变化趋势， 将本文模型和Webster信号配时方案代入公交乘客可靠度计算方法中， 将公交优先方向的流量设定为800辆·h-1, 公交优先方式和非公交优先方向的公交车比例分别为20%和10%. 图4为非优先方向流量变化下两个方向的公交乘客可靠度变化趋势. 可以看出， 随着非公交优先方向流量值的增加， 两个方向的公交乘客可靠度都在不断降低， 并且Webster信号配时方案下公交优先方向的公交乘客可靠度相对非公交优先方向下降更快， 而本文所提出的模型却没有出现此情况. 这是因为Webster信号配时方案没有考虑两个方向公交车比例的不同， 而本文所提出的模型在信号配时优化时考虑到公交优先方向公交车比例较大， 当非公交优先方向流量值不断增大时， 并不会分配非公交优先方向过多的绿灯时间.

图4 公交乘客可靠度与流量之间的关系

3.2 模型对比

假定公交优先方向的期望流量值为800辆·h-1， 非公交优先方向的期望流量值有3种情况(情况1、 情况2、 情况3)， 分别为400、 600、 800辆·h-1， 公交优先方向和非公交优先方向的公交车比例分别为20%、 10%， 且饱和流率均为1 800辆·h-1， 总损失时间为6 s. 本文模型与Webster信号配时方案对比， 结果如表3所示.

与Webster信号配时方案相比， 本文模型在较小的周期时长和绿灯时间情况下， 确保了可靠度不小于Webster信号配时方案. 因此， 本文所提出的模型是有一定效果的. 同时， 从表3可以看出， 当流量较大时， 可靠度提高较小. 可见当流量较大时仅依靠固定式信号控制已不能很好提高公交乘客可靠度， 还需进行主动优先控制.

表3 本文模型与Webster方案对比

3.3 仿真实验分析

图5 仿真场景Fig.5 Simulation scene

针对上文的信号配时方案结果， 本研究在VISSIM软件中模拟一个两相位控制的交叉口， 如图5所示， 输入相应的流量和信号配时方案.

运用VISSIM软件对Webster信号配时方案和本文模型控制下的交叉口进行测试， 选取车辆行程时间、 延误、 车辆排队长度3个指标作为评价指标. 两种信号配时方案的评价指标结果如表4所示.

从表4可以看出：

1) 总体来看， 相比于Webster信号配时方案， 本文模型控制下的公交优先方向和非公交优先方向的公交车辆平均行程时间分别降低了5.1%、 3.0%， 社会车辆平均行程时间分别降低了4.2%、 2.4%， 公交优先方向和非公交优先方向的车辆平均排队长度分别降低了16.7%、 10.5%. 由此可见， 该信号配时优化方法在提高交叉口车辆通行效益的同时， 更好地降低了车辆通过交叉口的行程时间损失和排队长度.

2) 本文模型控制下的公交优先方向和非公交优先方向的公交车辆平均延误分别降低了20.5%、 6.3%， 社会车辆平均延误分别降低了14.6%、 6.4%. 由此可见， 该信号配时优化方法在保证公交乘客可靠性的基础上， 有效提高了车辆的服务水平.

表4 两种配时方案下的评价指标对比

4 结语

本研究建立了基于公交乘客可靠度的信号配时优化模型， 并对公交乘客可靠度、 公交车比例与周期时长的关系进行分析， 研究非公交优先方向流量对公交乘客可靠度的影响， 最后通过与Webster信号配时方案的对比， 通过仿真验证所提出的模型具有一定的效果， 可为城市交通提供不同信号配时方法.

研究假定到达交叉口的公交车辆载客数固定， 如何实现载客数动态化处理还有待研究. 虽然通过公交运营数据拟合出的公交载客数比较符合正态分布， 但所建立的模型对于其他分布仍然适用. 此外， 考虑到公交车辆到达率具有不确定性， 假定公交车辆到达率为定值， 未来可结合公交车辆的地理位置信息探究公交车到达率对公交乘客可靠度的影响. 在实际的路网中， 随着交通流量的变化和路网状况的不同， 模型最适宜的应用范围还有待进一步研究.