利用多层感知机和I-V特性的光伏组件建模方法
2021-06-16余辉陈志聪郑巧吴丽君程树英林培杰
余辉, 陈志聪, 郑巧, 吴丽君, 程树英, 林培杰
(福州大学物理与信息工程学院, 微纳器件与太阳能电池研究所, 福建 福州 350108)
0 引言
近几十年来, 太阳能在全球经历了指数级的增长, 其中光伏发电是利用太阳能最普遍的方式[1]. 可靠、 准确的直流侧光伏组件建模对于优化整个光伏系统的设计和评估非常重要[2]. 作为光伏发电系统的核心, 光伏面板通常工作在复杂、 严峻的室外环境中, 在长期运行的情况下, 必然会导致光伏组件的性能下降. 常规的基于标称数据的光伏建模方法, 难以对实际工况下的光伏组件进行精确可靠的建模. 所以, 研究基于实际工作条件下光伏组件电流-电压(I-V)特性的建模方法具有重要的实际意义. 基于I-V特性的光伏建模方法通常包括基于等效电路的数学建模方法和基于机器学习的回归建模方法[3]两种.
光伏建模的数学方法需要搭建光伏组件的等效电路, 然后识别电路参数以及这些参数与环境条件(例如辐照度、 温度等)之间的关系. 光伏阵列基本上由串联/并联的太阳能电池组成, 并且太阳能电池实际上是将光转换为电流的光电二极管[4]. 因此, 基于等效电路的模型至少包含一个二极管和一个电流源. 根据二极管和寄生参数数量, 通常有单二极管五参数模型, 双二极管七参数模型和三二极管九参数模型[1, 5-6]. 这些方法识别出的参数对测量噪声非常敏感, 高度依赖现场测量的I-V曲线的质量, 并且这些参数识别方法只能在特定的工作条件下提取模型参数, 这可能导致建模的不确定性和不准确性. 总之, 基于等效电路的数学建模方法会受到等效电路的选择、 实际工作条件、I-V曲线的准确性以及确定模型参数与环境条件之间关系的极大影响[7].
基于机器学习的回归建模方法直接从实测数据通过回归方法建立模型, 与等效电路的方法相比, 不需要任何等效电路以及模型参数、 环境条件与模型之间的关系方程[8]. 一些典型的机器学习方法被用于光伏建模, 例如径向基神经网络(RBFNN)、 广义回归神经网络(GRNN)、 BP神经网络、 支持向量机(SVM)等[9-11]. 这些方法大多数使用辐照度、 环境温度以及实时电压来预测光伏组件的输出特性. 由于缺乏对原始数据的精细处理和对原始电气特征的设计, 这些方法的模型精度都受到了相当的限制. 本研究针对上述两种方法的不足之处, 提出一种精确的光伏组件建模方法. 首先对数据进行插值采样、 降采样减少数据冗余, 其次构造特征校正辐照度特征增强模型表征能力, 最后建立并训练多层感知机神经网络算法模型, 完成光伏组件I-V特性的精准建模.
1 数据集预处理
1.1 实测光伏I-V曲线数据集介绍

图1 安装在科罗拉多州Golden地区的光伏组件和测量设备Fig.1 PV modules and measurement equipment at Golden, Colorado
使用可公开获取的美国国家可再生能源实验室(NREL)提供的实测光伏组件I-V特性曲线数据集[12]来验证所提出的光伏建模方法的有效性. 该数据集包含一年中不同气候条件下三个不同地点的实测数据. 在本研究中, 使用的是安装在科罗拉多州Golden地区的光伏组件数据集, 数据的收集时间是2012年8月14日至2013年9月24日, 如图1所示. 该地区的数据集下有多种材料制成的光伏组件的实测数据, 包括单晶硅(xSi11246), 多晶硅(mSi0251), 碲化镉(CdTe75669), 硒化铜铟镓(CIGS1-001), 非晶硅(aSiMicro03038)和具有本征薄层的异质结(HIT05662). 使用现在光伏面板最常用的单晶硅(下文使用xSi代替)和多晶硅(下文使用mSi代替)的实测数据进行模型的训练和验证.
1.2 I-V曲线重采样
为了获得准确可靠的光伏模型, 应该对原始数据集进行合理的预处理, 以提高数据的质量. 在原始数据集中, 每条I-V曲线都包含大约200个数据点, 这些数据点是在大约I-V的几乎相等空间的电压阶跃处测量的. 但是, 众所周知,I-V曲线的最大功率点(MPP)远离短路(SC)点, 并且接近开路(OC)点, SC和MPP点之间的部分较为平坦, 但MPP和OC点之间的I-V曲线部分通常比较陡峭. 因此, 有很多分布在平坦部分的数据点包含相对较少的曲线关键信息, 但是分布在具有相对丰富关键信息的陡峭部分上的数据点却较少.
为减少数据冗余并且平衡I-V曲线数据点的分布, 提出一种利用线性插值的方法来重采样原始I-V曲线. 经过处理, 每条I-V曲线中包含的数据点数从原始的200个减少到最终的50个. 所提出的方法可以大大减少平坦部分的数据点, 同时在陡峭部分保留相对更多的数据点. 插值采样方法详细说明如下.
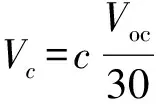
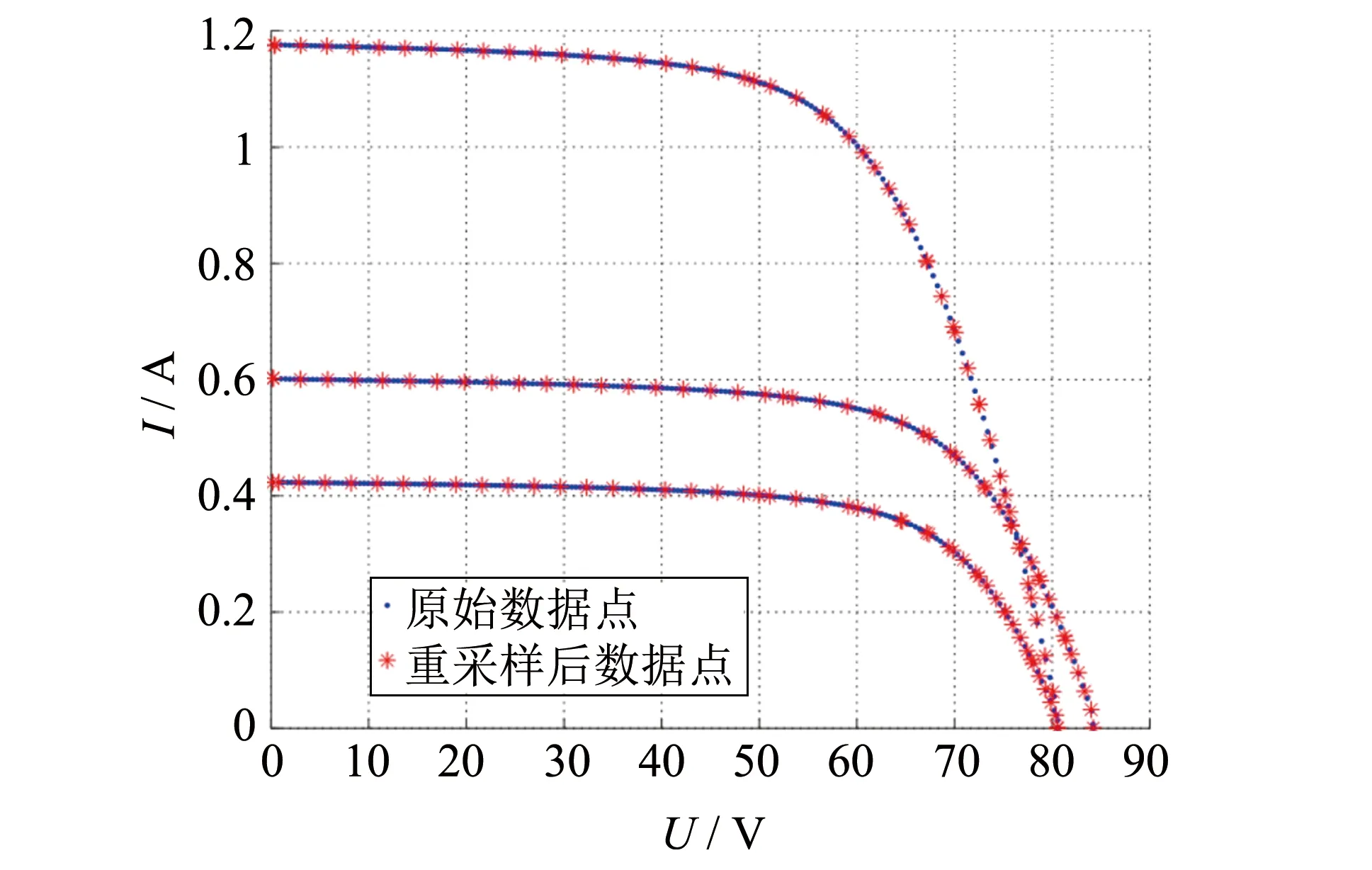
图2 重采样前后I-V曲线数据点对比Fig.2 Comparison of I-V curve data points before and after resampling
同理, 从每条I-V曲线等间隔的电流重采样20个数据点, 得到Id=dIsc/20(d=1, 2, …, 20), 通过线性插值方法获得与电流Id相对应的电压值Vd.
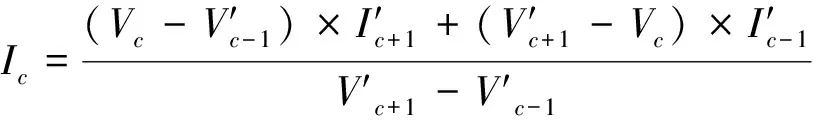
(1)

(2)
使用这种方法能够在0到最大电流Isc之间均匀采样20个数据点对.
最后, 通过按电压升序对采样得到的数据点进行排序, 形成新的重采样I-V曲线. 与原始曲线相比, 图2绘制了部分重采样的I-V曲线, 从中可以看出重采样曲线的数据点分布更为合理. 这样既能够减小数据冗余, 也能最大程度地保存关键点信息.
1.3 数据集降采样
原始数据集中, 数据样本的分布在环境条件方面并不平衡. 数据分布不平衡可能会导致模型在训练过程中的过拟合或者欠拟合, 从而影响模型的准确度. 为了平衡数据集中的环境条件, 采用基于辐照度和温度网格的降采样方法来挑选合理的I-V曲线, 这也可以在保持精度的同时大大减少数据量, 具体的降采样方法如下所述.
首先, 设置辐照度、 温度范围和间隔以确定采样网格. 辐照度和温度范围主要由原始数据集中的相应最大值和最小值确定, 而间隔则根据分辨率手动确定. 在这项研究中, 将辐照度网格数设置为60, 而将温度网格数设置为30. 其次, 根据辐照度和温度网格采样I-V曲线. 具体地, 根据辐照度对I-V曲线进行分类和划分, 然后根据温度对每个辐照度网格中的曲线进行分类和划分. 最后, 如果网格内存在曲线, 则在每个网格中随机选择一定数量的I-V曲线, 在本研究中将其设置为2条. 经过上述处理, 可将原始I-V曲线的数量从12 000条左右减少到1 300条左右.
2 基于多层感知机神经网络的光伏回归建模
2.1 多层感知机及Adam算法简介
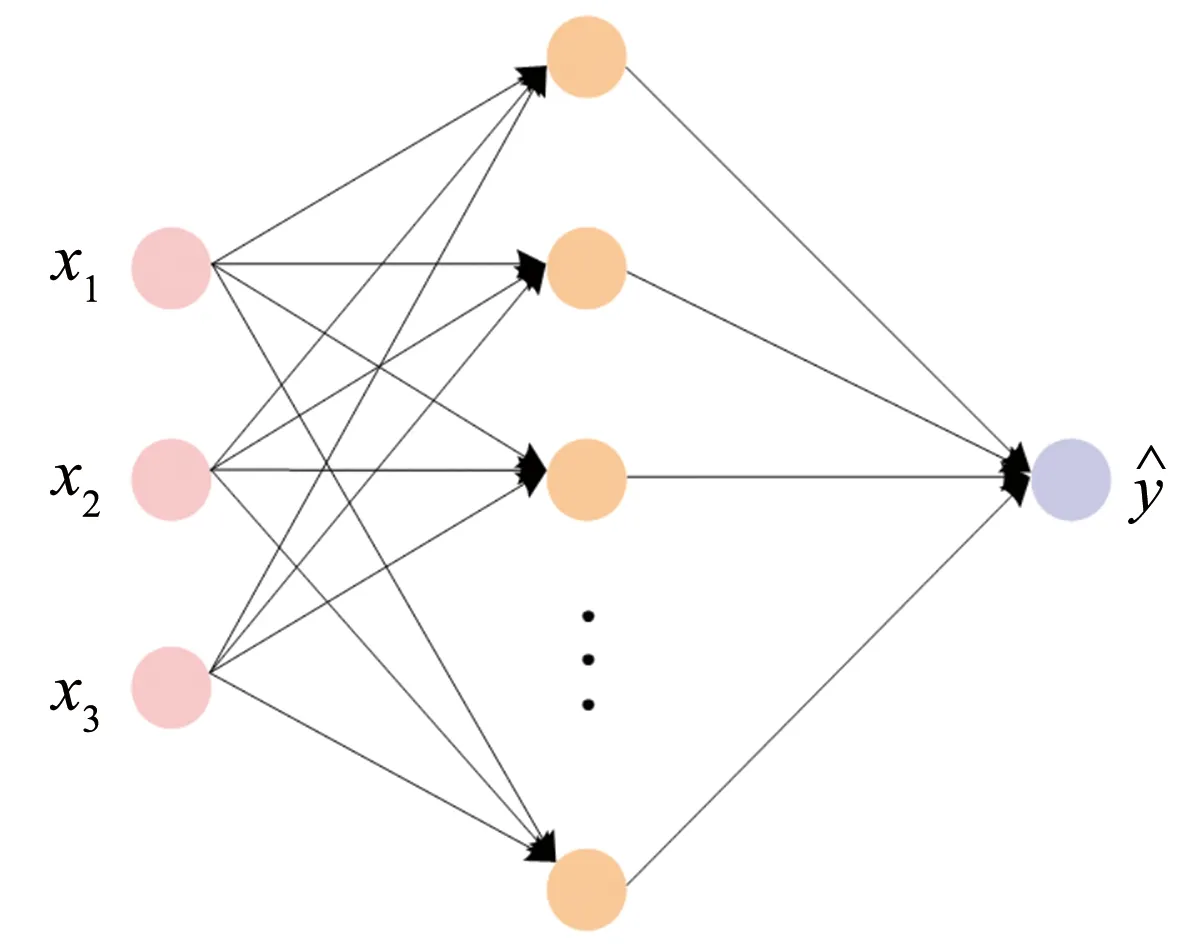
图3 含有一个隐藏层的多层感知机网络结构Fig.3 Multilayer perceptron network structure with a hidden layer
多层感知机(MLP)是一种常见的人工神经网络算法, 通常包含输入输出层和若干个隐藏层, 以回归问题的单隐层MLP为例, 其网络结构如图3所示.
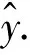
ai=g(w1ix1+w2ix2+w3ix3+bi)
(3)
假设隐藏层与输出层的连接权值为权重矩阵β, 激活函数为f(x), 偏置为常数值c, 那么网络的输出为:

(4)
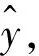
梯度下降法使用了损失函数的一阶导数信息, 存在收敛慢, 可能陷入局部最小值的风险. 所以本研究使用了Adam优化算法[13]来迭代求解模型参数. Adam算法记录了梯度的一阶矩和二阶矩, 并且使用动态的学习率衰减, 使算法能够快速准确地找到模型最优参数. Adam算法的伪代码如算法1所示.

算法1: Adam算法Require: 步长αRequire: 矩估计的指数衰减率, β1和β2在区间[0, 1)内Require: 参数为θ的随机目标函数f(θ)Require: 初始化参数θ0初始化一阶矩和二阶矩变量m0←0, v0←0初始化时间步t←0 while θt没有收敛 do t←t+1 gt←▽θft(θt-1) (计算目标函数在时间步t对参数的梯度) mt←β1 mt-1+(1-β1)·gt(更新一阶有偏矩估计) vt←β2vt-1+(1-β2)·gt2 (更新二阶有偏矩估计) m^t←mt/(1-βt1) (修正一阶矩的偏差) v^t←vt/(1-βt2)(修正二阶矩的偏差) θt←θt-1-α·m^t(v^t+) (更新参数) end whilereturn θt
2.2 光伏组件回归建模
2.2.1 模型输入特征选择
在数据处理的过程中, 是以I-V曲线为单位来进行处理的. 在实际的任务中, 往往是需要预测单个电流点的输出值, 需要将I-V曲线数据规整为合适的形式. 经过前面介绍的数据预处理方法处理后, 每个数据集原始的实测曲线由12 000条减少到1 300条左右, 而每条曲线包含50个电流-电压数据点对. 将每条I-V曲线拆分为50个数据样本, 这50个样本的环境参数(例如辐照度, 温度等)是相同的, 但是电压值不同, 预测的目标即电流值也是不同的. 这样, 每条I-V曲线就能拓展为50个样本, 方便后续的模型训练.
光伏发电系统是一个复杂的系统, 有许多因素可能会影响光伏组件的输出, 例如POA辐照度、 光伏组件的背面温度、 干球温度、 相对湿度、 大气压强等. NREL提供的实测数据集中包含上述多个环境因素, 其中相对湿度和大气压强的实测数据包含大量的缺失值, 如果剔除缺失数据的样本会导致关键信息的缺失, 但是若使用机器学习算法来预测这些缺失值又会引入新的误差, 所以将不考虑相对湿度和大气压强对光伏组件输出的影响. 在光伏建模中, POA辐照度和光伏组件的背面温度是与输出最相关的, 而其他因素可能有助于改善光伏组件的性能.
在实际的光伏系统中, 通常是使用一块小的光伏参考面板来测量辐照度数据. 如果参考板材质和光伏面板不同, 或者安装角度不同, 会导致辐照度测量误差. 基于此, 使用短路电流来校正辐照度, 校正辐照度的计算方法如下式所示:
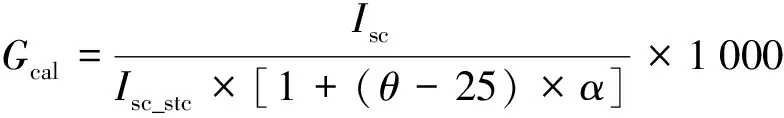
(5)
其中:θ是光伏组件的背面温度(℃);Isc是实际工作条件下的短路电流;Isc_stc是标准条件下的短路电流;α是短路电流的温度系数(光伏组件的数据手册提供).
另外, 研究了其他环境因素与光伏系统输出之间的相关性, 发现在建模过程中, 同时使用光伏组件的背面温度和干球温度更能准确表征光伏组件的输出特性.
最终, 使用校正的POA辐照度Gcal、 光伏组件的背面温度θb、 干球温度θd以及光伏组件实时输出电压V来预估光伏组件的输出电流I.可将上述的描述归纳为:
I=f(Gcal,θb,θd,V)
(6)
模型的任务就是找到一个合适的映射f, 使预测的电流与实际输出电流之间的误差尽可能小.
2.2.2 最优模型结构
使用的多层感知机模型包含一个输入层, 两个隐含层以及一个输出层. 其中: 两个隐含层都包含300个神经元. 隐含层的激活函数都是Sigmoid函数, 其表达式为:
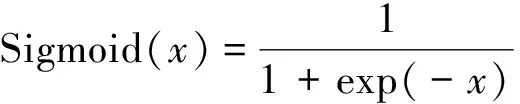
(7)
模型的损失函数为均方误差MSE, 优化算法为Adam算法. 迭代次数为100轮. 最终用于建模的网络结构及网络的输入输出如图4所示.
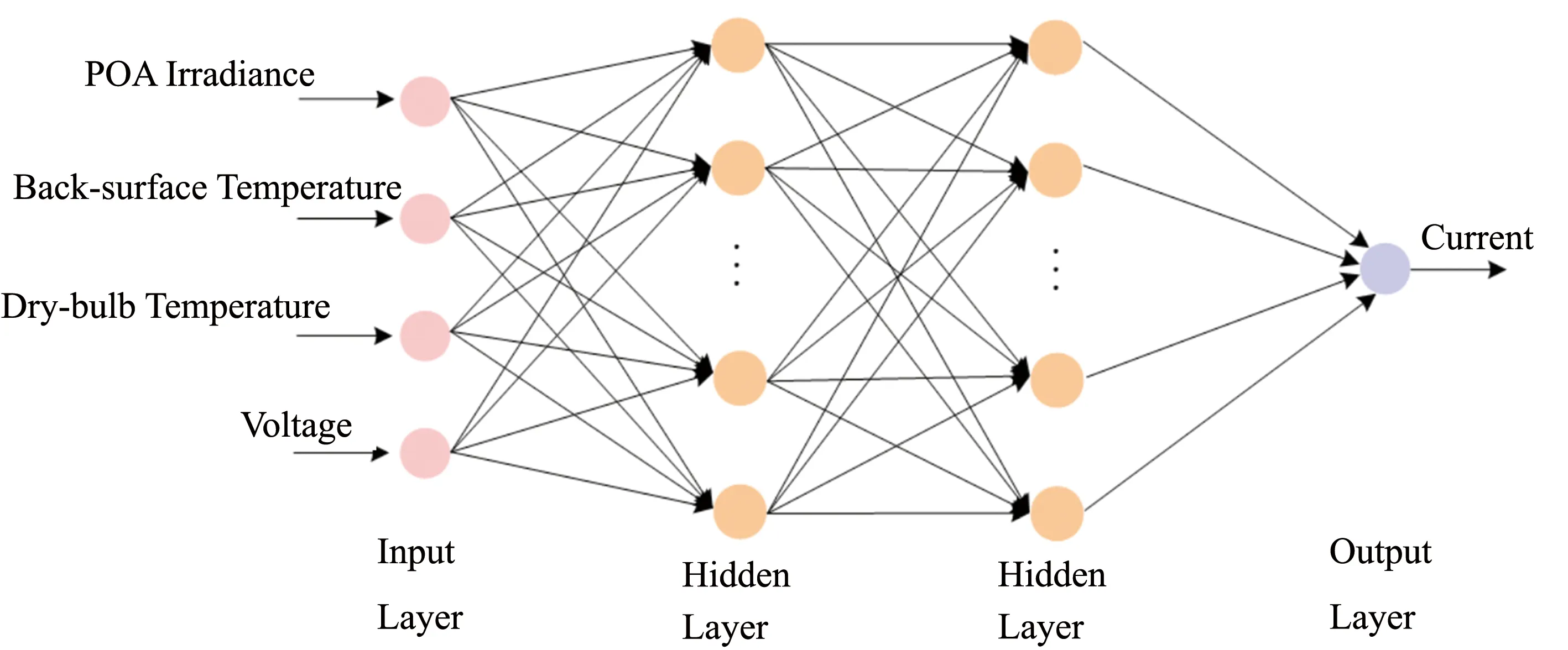
图4 光伏建模的实际网络结构Fig.4 Actual network structure of photovoltaic modeling
3 实验验证
3.1 性能指标
使用均方根误差(RMSE), 平均绝对误差(MAE)以及判定系数(R2)三个性能指标来评判模型的效果, 它们的计算公式如下所示:
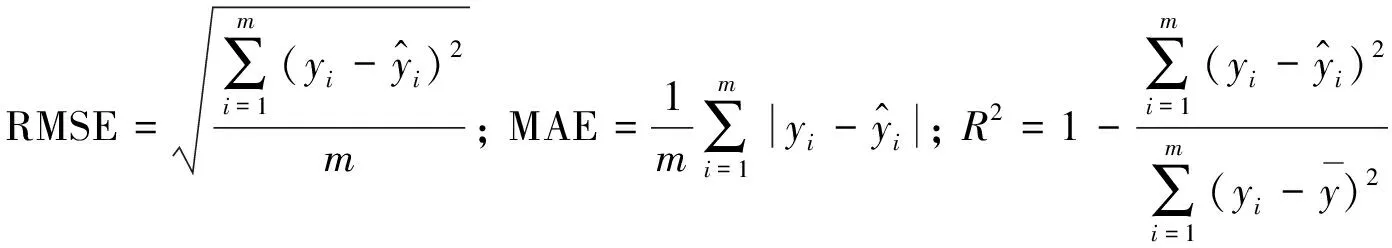
(8)
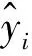
3.2 实验结果
3.2.1 数据预处理效果验证
为验证数据预处理的有效性, 设置实验来对比模型的预测性能. 在降采样过程中, 将12 000条I-V曲线减少到1 300条左右. 由于训练集和测试集来自于降采样后的1 300条I-V曲线, 如果采样不均匀, 丢失了关键信息, 可能会导致模型对其余的I-V曲线数据预测效果差. 基于上述原因, 在不包含测试集曲线的原始数据集中随机采样10次, 得到10个与测试集大小相同的随机采样测试集. 使用训练好的模型分别对10个随机采样测试集进行预测, 平均误差结果如表1所示. 可以看到, 在三个用于评估模型的性能指标上, 相差只有约0.02%, 证明降采样在降低了数据冗余的同时能够很好地保留了数据集的关键信息.
使用不处理的原始数据集进行建模, 得到如表2所示的实验对比结果. 实验表明, 没有预处理的数据包含较多的脏数据和较大的冗余, 会导致建模精度降低, 而采用本方法预处理后显著地提高了模型的准确度.
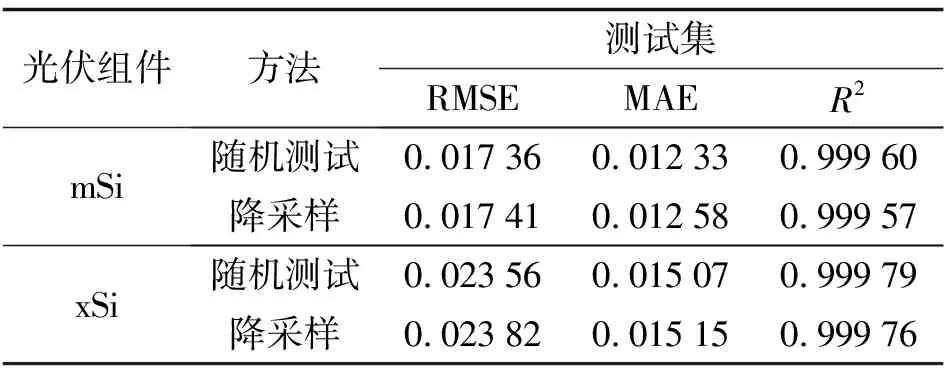
表1 降采样与随机采样的测试集性能对比

表2 有无预处理的模型性能对比
3.2.2 算法对比
为验证模型的有效性, 本研究与一些典型的算法进行对比, 例如支持向量回归(SVR)和梯度提升决策树(GBDT). 为保证实验的无偏性, 已将三个算法都调整到最优的参数. 其中, SVR的最优参数为: 径向基核函数, 核函数的gamma值为5, 损失函数的ε值为1, 其他为默认参数; GBDT的最优参数为: 800棵决策树, 每棵树的最大深度为5, L2正则项系数为5.0, 其他为默认参数; MLP算法最优参数已在上一章给出. 使用谷歌的开源Tensorflow库来搭建网络模型, 使用开源的GBDT算法实现lightGBM库[14]来实现GBDT算法, 使用libsvm库[15]来实现SVR算法. 实验结果如表3所示.
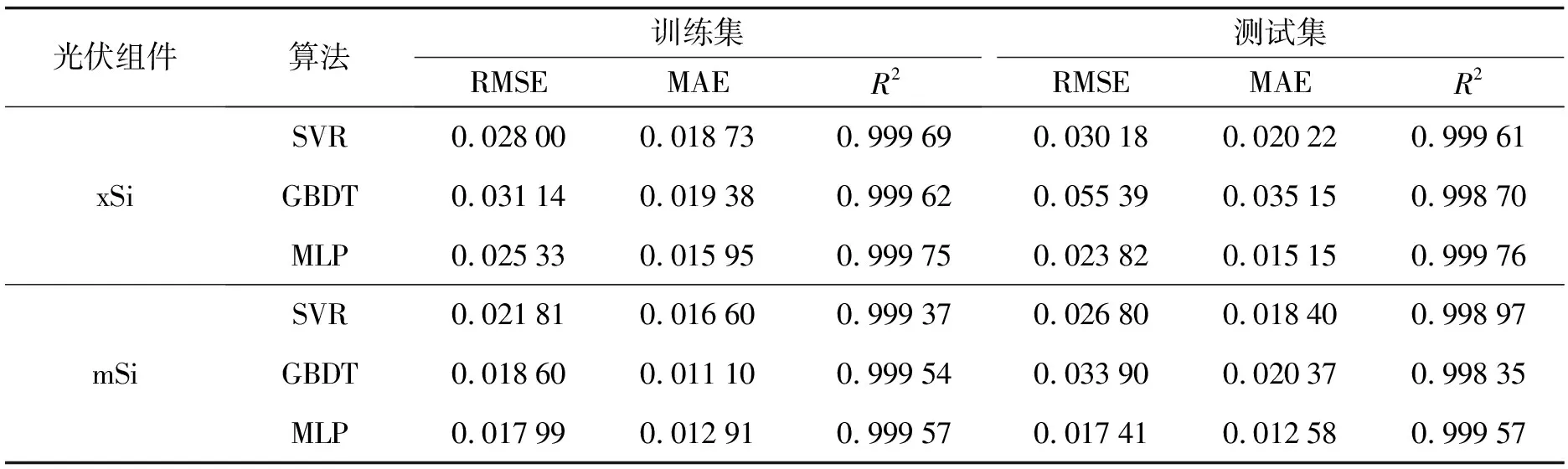
表3 三种算法的平均性能指标
在模型得到的预测值的基础上, 绘制了实测I-V曲线与模型预测I-V曲线的对比图, 如图5所示.
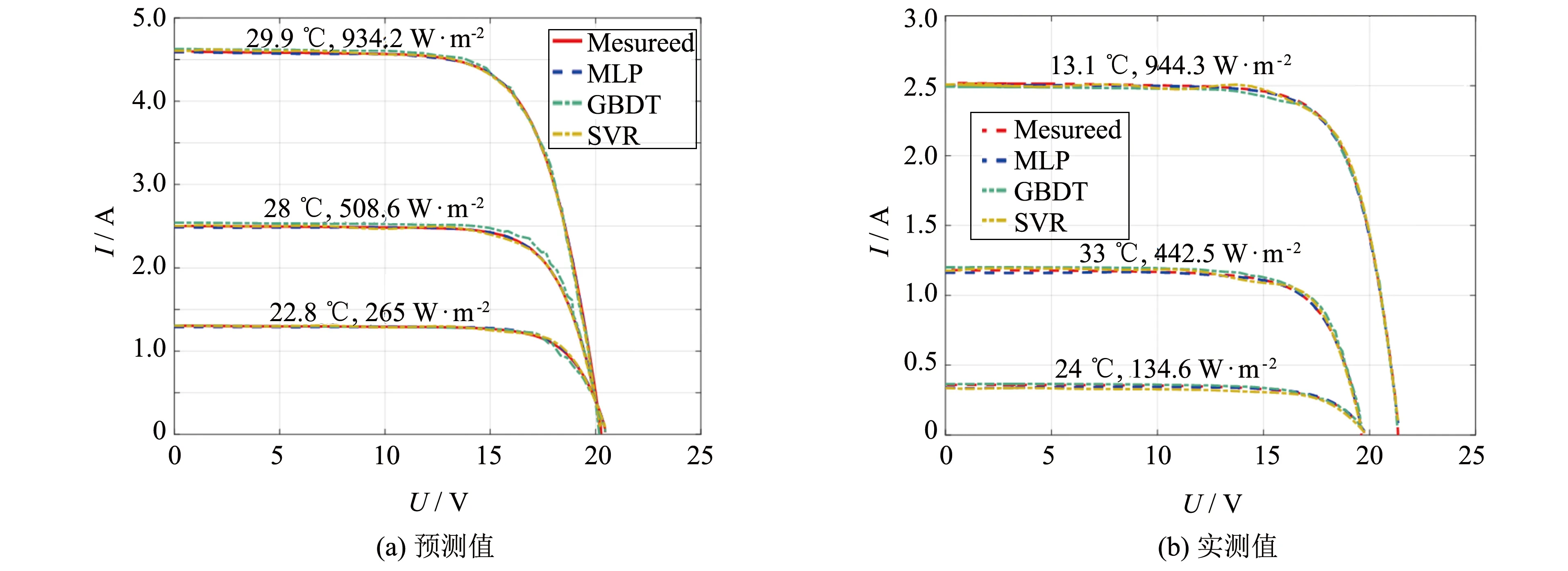
图5 网络的预测值与实测数据对比Fig.5 Comparison of the predicted value of the network with the measured data
4 结语
提出一种利用多层感知机神经网络和I-V特性曲线数据集的光伏组件精确回归建模方法. 首先, 使用双线性插值法对实测I-V曲线进行重采样, 以提高I-V曲线上数据点分布的均匀性; 进而, 使用基于温度-辐照度的网格采样法对I-V曲线数据集进行下采样, 降低数据冗余度; 最后, 提出一种基于双隐层多层感知机神经网络的光伏组件模型结构, 并基于预处理的I-V曲线数据集, 使用Adam算法训练该模型. 与常规的建模方法相比, 本研究使用高效的数据预处理方法, 校正了原始测量POA辐照度, 并且考虑了光伏组件背面温度和干球温度对其输出的影响. 基于NREL实测I-V曲线公开数据集的实验结果证明, 本研究提出的建模方法在测试集上的RMSE能低至1.7%~2.3%; 在两种光伏组件的数据集上, 相比SVR算法误差平均降低了28%, 相比GBDT算法误差平均降低了52%, 并且有很好的泛化性能.
