基于恶劣场景辨别法的微网随机自适应鲁棒模型

谌江波，陈碧云，王楚通

(1.南京工业大学浦江学院，南京 211200；2. 广西大学广西电力系统最优化与节能技术重点实验室，南宁530004；3. 浙江大学电气工程学院，杭州310027)

0 引言

随着分布式电源(distributed generator, DG)接入电网比例的不断提高，其出力的随机性和间歇性对电力系统的安全稳定运行构成威胁[1 - 2]。微网凭借先进的智能计量技术、协调控制技术以及信息通信技术，为有效解决DG并网提供了新的思路[3 - 4]。然而，由于电价的波动性和风光出力的随机性，不平衡惩罚依然存在，微网参与市场竞标仍存在很大的风险。

微网往往聚合可再生能源、储能、需求响应(demand response, DR)等多种分布式能源，通过协调内部各机组出力，实现作为一个有机整体参与电网运行与调度，极大减小了分布式电源单独并网对公网造成的冲击，并提高了其市场竞争力[5]。目前，对于微网问题的研究关键在于对不确定性因素(风电、光伏、市场电价)的处理以降低微网面临的失衡风险。文献[6 - 9]采用随机规划法处理风电、光伏出力的不确定性，通过给出不同出力情景下的概率分布，提高了计算结果的适应性。尽管随机规划法提高了模型计算结果的适应性，但是微网系统中的风电、光伏概率分布规律往往难以预测，且随机规划法引入了大量的计算场景，导致计算量过大，求解效率较低。文献[10 - 12]采用静态鲁棒优化法对不确定性因素进行处理，通过将不确定性划分在一个可能的最大区间，且无需知道不确定因素的概率分布，弥补了随机规划法的不足。但是静态鲁棒优化往往考虑最极端情况的收益，因此其求解结果过于保守。

两阶段鲁棒优化调度模型能够在仅知道不确定性因素边界值的基础下，严格保证极端条件下的系统运行可靠性，并通过动态迭代降低保守性，克服了静态鲁棒优化的缺点[13 - 15]。目前，两阶段鲁棒优化模型已经被应用于电力系统优化调度的各个领域。文献[16]将两阶段鲁棒优化法运用到机组组合问题中，通过构建三层max-min-max模型将机组组合问题转换为两个阶段的决策问题，并通过Benders算法进行模型的解耦计算。文献[17]考虑市场电价的不确定性，将两阶段鲁棒优化模型运用到电力市场的出清模型中，并通过列约束生成法(column and constraint generaion, CCG)将三层模型进行解耦，与静态鲁棒优化相比，两阶段鲁棒优化模型降低了求解结果的保守性，模型的适用性更强。

目前求解自适应鲁棒优化问题主要有4种思路：1)仿射算法[18]；2)Benders分解算法[19]；3)列约束生成法[20]；4)场景法[21]。首先，仿射算法利用线性决策规则建立决策变量与不确定参数之间的仿射关系，从而将两阶段问题转化为单阶段优化问题，但是结果较为保守；Benders分解算法以及列约束生成法在线性化过程中会引入大量的边界参数和整数变量，导致问题规模较大时模型求解复杂；场景法需要列举大量不确定场景集合，导致计算的效率偏低，求解时间过长。基于此，本文提出一种基于恶劣场景识别法的两阶段鲁棒优化求解算法，该方法将列约束生成法CCG算法与场景法结合，既避免了CCG算法线性化过程中引入大量边界参数和整数变量的弊端，也弥补了基于场景法求解效率偏低的问题。具体方法是将原来的三层优化问题分解为主问题和子问题进行迭代求解，主问题求解关键场景集下的微网单层优化模型，子问题则用来辨别恶劣场景集，从而极大地削减了求解所需的场景数量，提高了算法的求解效率[22]。在此基础上，考虑微网同时参与日前能量市场(day-ahead energy market, DAM)、实时能量市场(real-time energy market, RTM)以及碳交易市场(carbon trading market, CTM)的情况，进一步探究了微网的利润影响因素， 恶劣场景集对优化结果的影响以及恶劣场景辨别算法在保留不确定性上的优势，验证了该算法的有效性。

1 微网日前阶段经济调度模型

1.1 目标函数

设微网模型由光伏机组、电储能系统(electric energy storage system, ESS)，燃气轮机组以及可中断负荷组成，设计微网同时参与日前能量市场与实时能量市场，目标函数为微网发售电的最大化利润，包括在日前市场的收入以及供负荷收入，并扣除燃气轮机、需求响应补偿成本以及碳交易市场成本：

(1)

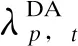
1.1.1 需求响应的补偿费用成本

现阶段，微网可通过电价引导用户侧进行需求响应，如在负荷高峰以及电价高峰，微网可通过向负荷支付一定补贴电价引导用户侧需求响应，常见的用户侧需求响应负荷类型为可中断负荷以及可转移负荷，考虑到本文的负荷单元性质为工业负荷，故以可中断负荷形式作为需求响应的代表形式。按照负荷中断对于用户的不同影响，将中断负荷分为不同的等级对用户进行补偿，需求响应补偿成本可以表示为[23]：

(2)

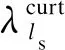
1.1.2 微型燃气轮机的运行成本

燃气轮机的成本曲线可表示为：

(3)

式中a、b、c为燃气轮机的成本系数。考虑到模型求解的高效性，尝试将燃气轮机成本曲线线性化，线性化后的成本曲线如式(4)所示。

(4)

其中

(5)

1.1.3 碳交易市场成本

碳交易机制作为一种市场化调节手段，能够有效削减电力行业的碳排放量，促进节能减排技术的发展。微网中的碳排放主要来源于燃气轮机机组，其碳排放量可以表示为：

(6)

式中：EC为微网实际碳排放量；σi为第i台燃气轮机机组的碳排放强度。

本文基于上海市发改委出台的有关碳排放配额分配方案，采用基准线法确定微网的碳排放配额。

(7)

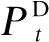
因此，微网的碳排放成本可以表示为：

Cc=λc(EC-ED)

(8)

式中：Cc为微网碳排放成本；λc为碳交易价格。

1.2 约束条件

1.2.1 燃气轮机约束条件

1)机组出力约束

(9)

(10)

(11)

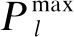
2)机组爬坡率限制

(12)

(13)

式中rU、rD为燃气轮机的向上、向下爬坡率。

3)机组启停变量限制

(14)

(15)

(16)

(17)

4)机组最小关机时间约束

(18)

(19)

式中：tsu、tsd分别为燃气轮机组的最小开关机时间；tsu,0、tsd,0分别为燃气轮机组的初始开关机时间。

1.2.2 电池储能约束

(20)

(21)

(22)

(23)

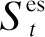
1.2.3 日前市场交易量约束

(24)

(25)

式中PDA,max、SDA,max为微网在日前市场的最大购售电量。

1.2.4 可中断负荷约束

(26)

(27)

(28)

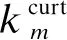
1.2.5 功率平衡约束

微网内各发电单元和各用电单元应保持供需平衡，其功率约束式为：

(29)

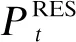
至此完成了微网日前阶段建模，所建模型为混合整数线性规划模型(MIP)模型。

2 微网两阶段鲁棒优化调度模型

2.1 微网两阶段鲁棒优化模型

考虑到市场电价随时间的波动性具有明显规律，可通过各类预测方法对其进行精确预测，从而减少其对于微网调度的影响。针对光伏出力难以预测、随机性强等特点，考虑研究最恶劣场景下的光伏出力，通过两阶段鲁棒优化法对其进行求解。

在日前市场阶段，微网在光伏出力等不确定因素确定之前进行决策，决策目标是微网利润最大化，决策变量包括燃气轮机组的启停以及与日前市场的交易电量[24]。

在实时市场阶段，微网在不确定因素实现之后进行决策，微网在所有光伏出力场景中，选择最恶场景下的光伏出力从而得到最小的微网利润。

最后，在日前决策变量和最恶劣光伏场景确定后，微网以最大化利润进行实时市场交易量决策与其他变量决策。

为方便表示，微网两阶段鲁棒优化模型可定义为模型M1，因此，M1表示为三层结构max-min-max形式。

2.2 目标函数

(30)

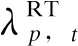
与日前调度模型相比，微网两阶段鲁棒优化模型在日前市场阶段考虑了电价场景，日前决策变量特征为均含有下标p、t；在实时市场阶段考虑了电价场景和光伏场景，实时决策变量特征为均含有下标p、t、s。

2.3 约束条件

1)微网日前运行约束：式(9)—(28)

2)微网实时调整运行约束

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

(42)

(43)

(44)

(45)

(46)

3 基于恶劣场景辨别的模型求解算法

3.1 恶劣场景概念及现实意义

事实上，从式(30)可以看出，整体目标函数包括两部分，包括第一阶段基准场景下的日前优化调度收益最大化，由于基准场景一般给定，所以第一阶段为确定性的优化模型。第二阶段考虑了所有可能出现的光伏场景，设该场景集合为Ω， 第二阶段的min-max问题其实质含义为，假设Ω集合中共计有ns中光伏场景，则内层max求解的是每一个光伏场景微网的实时调度收益最大化问题，共计有ns种最优解，分别对应不同场景。而外层的min主要用于辨别这ns种场景下使得微网实时收益最低的场景，若假设当取场景si时，对应的微网实时调度收益在所有场景中最低，则可认为此时的si最恶劣场景，也称恶劣场景。

从现实意义上来讲，所谓最恶劣场景，就是使得微网实时调度收益最低的场景，例如，当光伏出力波动较大，在本该出力较高的10-16时，由于天气等原因，此时光伏出力值较低，为了满足较高的负荷需求，微网在此时需要增加向电网的购电电量或增开燃气轮机组等其余发电设备，相较于成本较低廉的光伏发电，该举措使得微网的发电成本增加，从而其收益有所降低。

3.2 内层min-max模型的解耦

微网两阶段鲁棒优化模型的下层min-max模型难以直接求解，需要采用恶劣场景辨别法将其转换为单层优化模型求解。首先，根据历史数据定义不确定性集合W由一系列代表性场景构成。然后，针对含有有限数量场景的集合W，引入辅助变量βMP表示实时运行阶段的最恶劣的场景下min-max问题的解耦。为方便表示，定义基于解耦替换的两阶段鲁棒优化模型为M2，其目标函数如式(47)所示。

(47)

式中辅助变量βMP满足约束：

(48)

定义M2中代表性场景集合为W={w1,w2,w3…,ws}， 其中s为光伏出力的代表性场景数量，M2模型的其他约束条件如下：

1)日前运行约束：式(9)—(28)

2)实时运行约束：式(31)—(46),∀s∈W

通过引入代表性场景和辅助变量，三层优化问题M1模型被转换为单层优化模型M2。相比于采用列约束生成法以及Benders分解算法相比，避免了内层min-max问题解耦时出现大量的非线性项，从而需要运用Big-M法引入大量0-1变量来进一步线性化，降低了模型的求解难度，提高了求解效率。

3.3 基于恶劣场景辨识的迭代求解算法

从上述分析中可以看出，每个代表性场景将引入额外的辅助变量和辅助约束式，当模型较为复杂，场景数较多，M2的计算仍然是一个复杂的多场景规划问题，难以直接求解。微网两阶段鲁棒优化模型研究的是所有光伏出力场景中最恶劣的情况，因此不确定性集合W中只有少数场景(恶劣场景)起到关键的作用。

基于此，文章提出一种微网两阶段经济调度模型主问题与子问题交替求解的迭代算法，从而快速识别最恶劣场景集，达到快速求解的目的。主问题仅考虑在最恶劣场景集(W的子集)下的M2单层优化问题，用于求解子问题辨识出来的恶劣场景下的日前及日内的决策变量，子问题用于辨别最恶劣的光伏出力场景，具体的迭代步骤如下。

1)根据日前光伏预测值设定潜在恶劣场景子集Ωw={w0}；

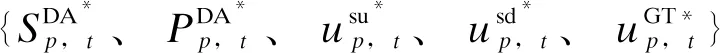
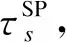
(1)目标函数：

(49)

(50)

(2)实时运行约束：式(31)—(46),∀s∈ΩΩW

4)设置迭代收敛判据

比较主问题βMP与子问题τSP的大小，若βMP≤τSP， 则说明关键场景集中的最恶劣场景已经包含所有场景的不确定性信息，转至步骤5；否则将最恶劣场景ssp添加到关键场景集ΩW={ΩMP,ΩW}中，转至步骤2，继续迭代，直到满足要求。

5)输出步骤2中求解主问题所得的最优调度结果。

3.4 迭代算法流程图

在基于恶劣场景辨别的迭代算法中，主问题主要用来求解关键场景集ΩMP下的微网最大利润，子问题通过识别最恶劣场景ssp并添加到关键场景集ΩMP中，从而大幅度削减需要计算的场景数量，具体算法流程如图1所示。

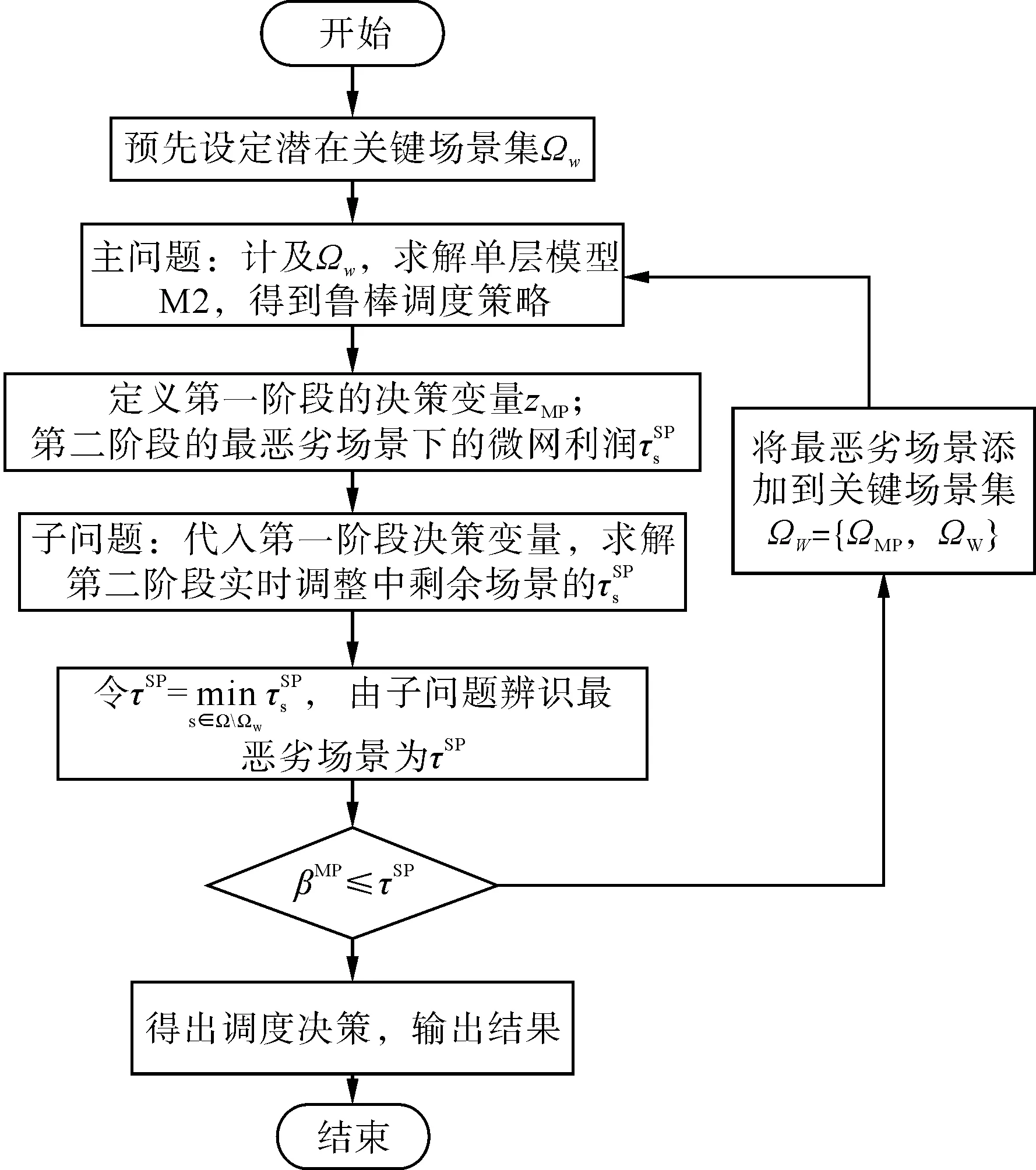
图1 两阶段鲁棒优化算法求解流程

4 算例分析

4.1 模型参数

本文的微网内部发电单元有燃气轮机组、光伏机组、电储能系统以及可中断负荷单元。微网参与日前能量市场和实时能量市场竞标，调度时长为1天，共分为24个小时段。

燃气轮机以及电储能系统的参数如表1、表2所示。可中断负荷分为3级，每一级可中断量设置为总负荷的8%，每级的补偿价格为38欧元/MWh、42欧元/MWh、50欧元/MWh。光伏出力选取北欧某地区典型日光照强度预测值，采用蒙特卡洛模拟法生成64组光伏出力代表性场景，如图2所示。微网负荷需求如图3所示，日前能量市场电价及实时能量市场电价如图4、图5所示。

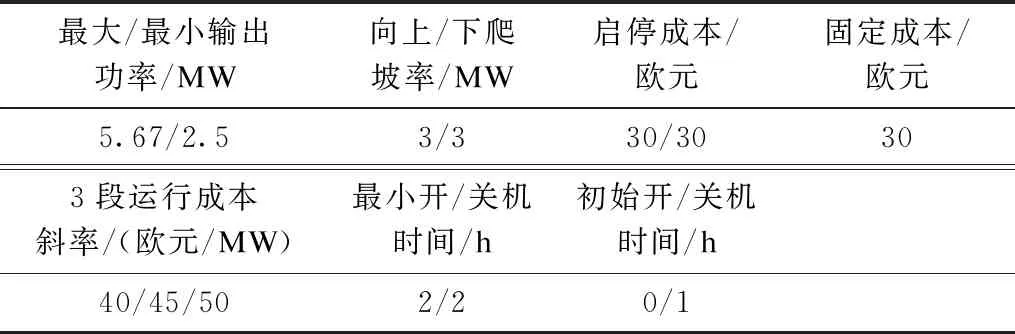
表1 燃气轮机参数

表2 电储能系统参数

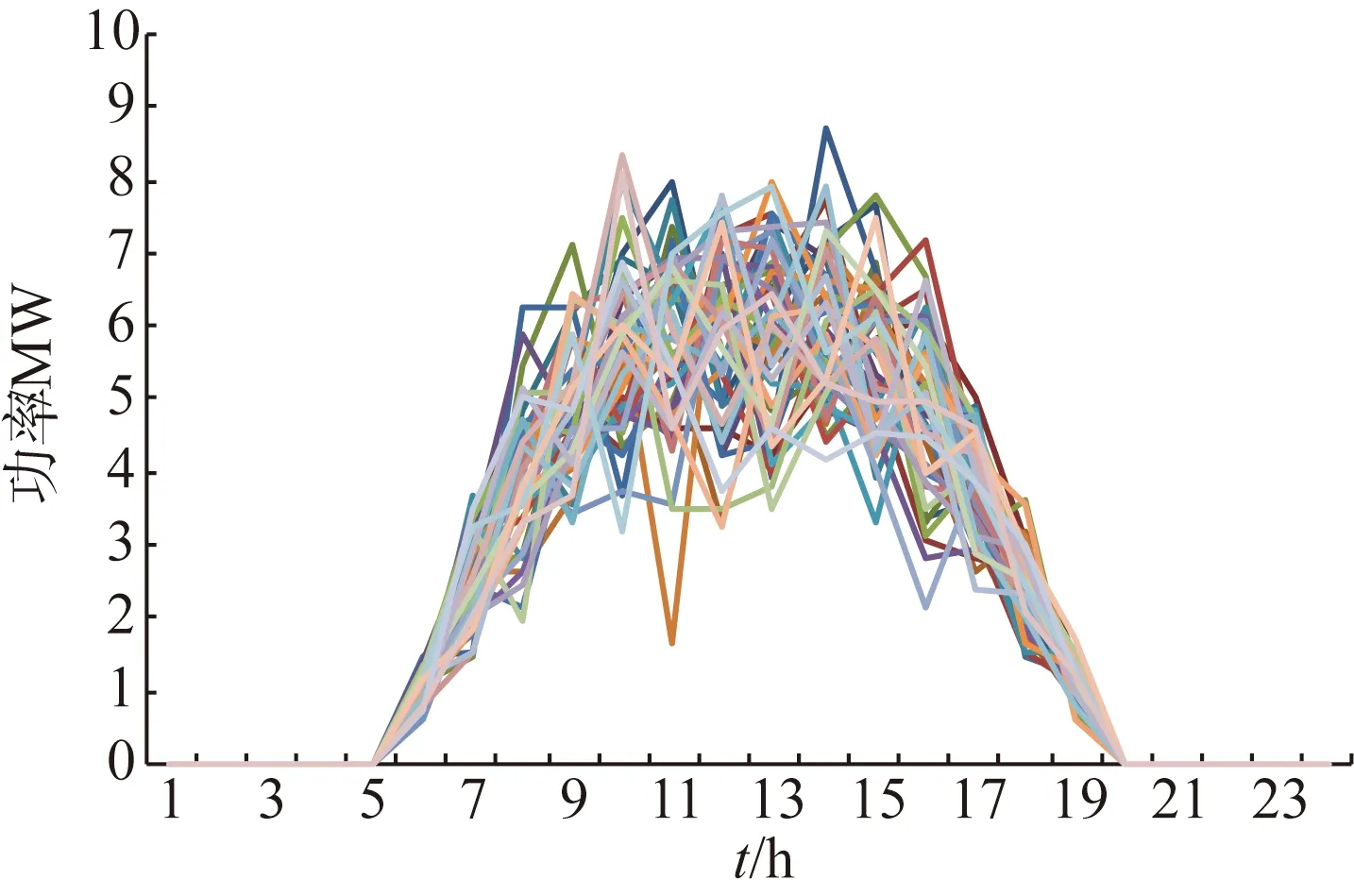
图2 64组光伏出力情景

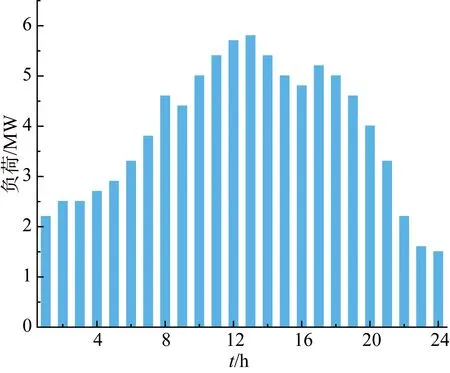
图3 用户负荷需求

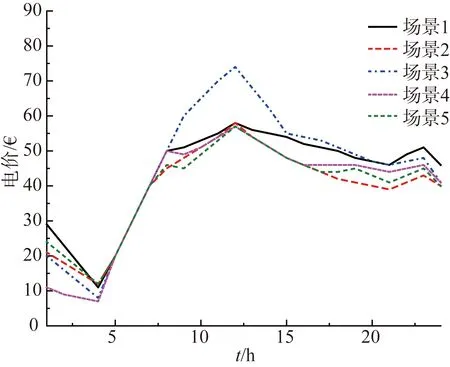
图4 5种场景下的日前市场电价

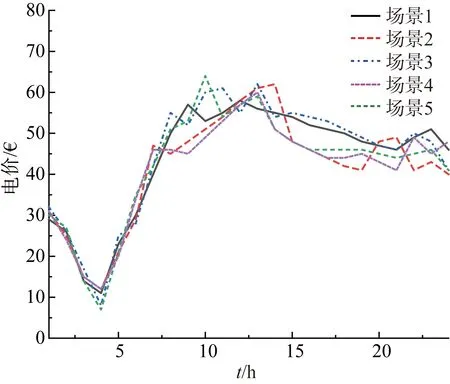
图5 5种场景下的实时市场电价

经过分解后，微网两阶段鲁棒优化模型可通过MATLAB调用CPLEX求解器进行求解。CPLEX软件主要用于求解单层优化问题，MATLAB调用CPLEX求解结果从而形成迭代求解。

4.2 算法性能分析

4.2.1 迭代结果分析

本文采用恶劣场景辨别法对迭代模型进行求解，恶劣场景辨识过程中日前能量市场收益、实时能量市场收益以及微网总收益如图6所示。

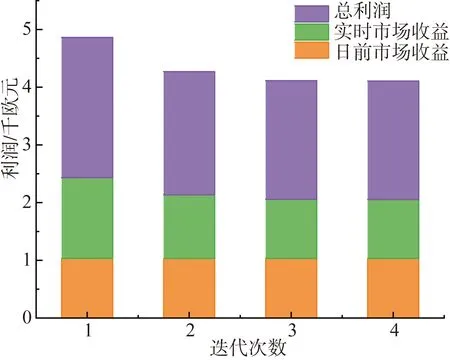
图6 迭代过程中的收益情况

从图6中可以看出，仅仅通过4次迭代即可识别出最恶劣的场景集合Ωw， 迭代过程中，由于日前市场收益是在光伏场景确定之前实现的，仅与基准场景有关，因此，在4次迭代过程中，日前市场收益值保持不变；实时市场收益第一次迭代从1 399.6欧元降低到1 103.1欧元，而后保持相对稳定，最终在第4次迭代后达到稳定值1 021.4欧元。

与此同时，微网总收益在第一次迭代后也有大幅度下降，从2 431.1欧元下降到2 135.8欧元，最终在第4次迭代后稳定于2 053.0欧元。这主要是因为实时市场收益主要取决于最恶劣的场景，该场景在第2次迭代中被子问题识别，随后被加入到恶劣场景集合中，因此在计算过程中，实时市场和总微网收益值有了大幅度下降。4次迭代后的恶劣场景集合为Ωw={s0,s13,s24,s31}。

4.2.2 关键场景对优化结果的影响分析

通过迭代求解后，本文将64组代表性光伏出力场景缩减为4组恶劣场景集合，剩余60组场景则为非关键场景。为证明剩余的60组非关键场景集对最终结果没有影响，本文设置以下几个案例进行分析研究。

案例1：模型M2仅考虑本文所辨别出来的4组关键场景集合(4组场景)；

案例2：模型M2考虑4组恶劣场景加20组非关键场景集合(24组场景)；

案例3：模型M2考虑4组关键场景和任意60组非关键场景集合(64场景)。

采用经典规划算法对案例1-3进行求解，记录求解结果和求解时间如表3所示。

由表3可知，案例1-3的优化结果完全相同，这表明非恶劣场景对优化结果没有影响。比较结果显示了仅考虑关键场景集的案例1不仅能够准确的替代考虑64组复杂光伏出力情形，并且由于削减了大量的非关键场景，案例1与案例2、案例3相比节约了了大量计算时间，当场景集规模增大时，这种效果尤为明显。

表3 不同场景集下的优化结果比较

4.2.3 算法计算效率测试

为进一步验证所提出的算法在求解效率上的优势，经过分解后，三层max-min-max问题被分解为单层优化模型M2，为形成对比，我们引入大量光伏场景进行试验，具体实验案例如表4所示。

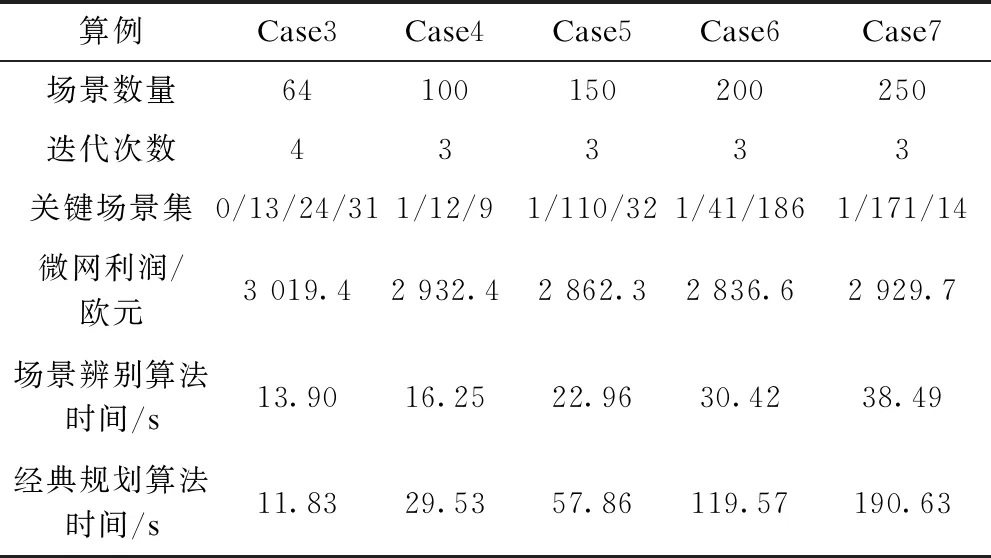
表4 不同案例下优化结果

从表4中可以看出，场景数量较少的时候，常规算法求解效率较高，计算简便，可以看到在200个场景以下时，常规算法均有一定的适用性；然而随着场景数量的不断增加，常规算法的计算时间大幅增长且增长速度很大，尤其是超过200个场景后，其计算时间达到了119 s，计算效率较低；相反，恶劣场景辨别法在场景数量较多的时候，增长速度缓慢，计算效率依然保持很高的水平。这主要是因为，增加的场景数量中，起到关键性作用的场景数量并不多，因此只需要增加较少的迭代次数便可以辨别出恶劣场景，从而削减了大量非关键场景集合，极大程度上节约了计算时间。取250个场景为例，此时采用恶劣场景辨别法的计算时间仅为38.49 s，而采用常规解法的计算时间为190.63 s，计算时间相差了近5倍，因此，恶劣场景辨别法更适用于大规模场景计算，具有较高的求解效率。

4.3 微网日前、实时调度情况分析

4.3.1 微网利润影响因素分析

本文考虑微网同时参与日前市场、实时市场以及碳交易市场，此外，还将可中断负荷纳入到微网的运行调控中，为分析微网在不同实验场景下的利润变化情况，本文设计如表5所示的实验方案。

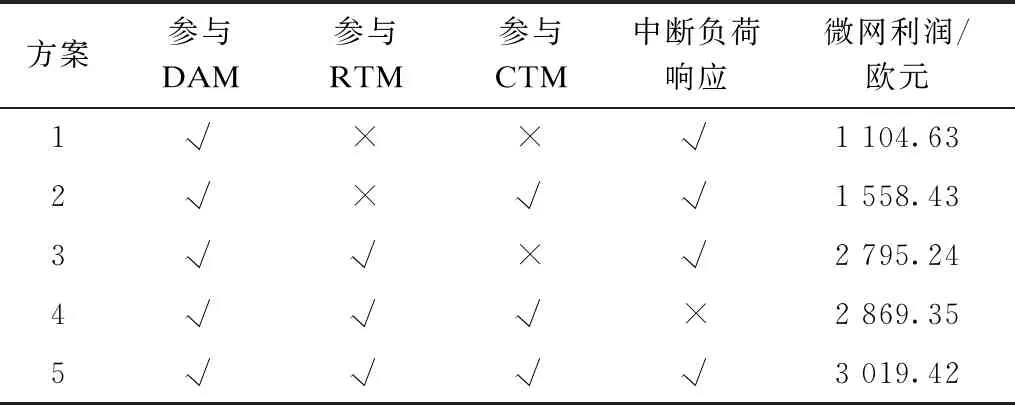
表5 不同影响因素下的微网利润比较

对比上述实验方案可知，当微网仅仅参与日前能量市场时，其收益值最低，仅为1 104.63欧元，在此基础上，考虑微网参与CTM以及聚合中断负荷响应，此时微网利润有所提升，但是增幅并不是很明显。案例3考虑微网同时参与RTM，此时微网利润提升明显，即使不参与CTM其利润增长也十分可观，这主要是因为方案1与方案2中均不涉及RTM，微网参与电力市场的方式单一，无法根据日前电价与实时电价灵活的做出购售电策略，因此利润较方案3有所降低。此外，可以看到，当微网同时参与DAM、RTM以及CTM时，聚合中断负荷响应也可以一定程度上提高微网收益。

4.3.2 微网内各单元出力情况分析

图7显示了微网内各功率单元发用电情况，从图中可以看出，当负荷高峰期时，光伏出力难以满足负荷需求，因此燃气轮机在负荷需求高峰时期保持满发状态，同时，为了进一步保证用户负荷得到满足，此时储能系统开始放电，当负荷高峰结束后，储能系统由放电状态转为充电状态，储蓄电量以应对下一个负荷高峰，此时燃气轮机也保持停机状态，用户负荷可由微网从上级电量购买电量满足，亦可考虑由中断负荷来满足。

图7 微网内各功率单元发电情况

微网的可中断负荷量如图8所示，由于中断等级越高，补偿费用越高，因此二级和三级中断负荷只在负荷需求高峰时期中断。

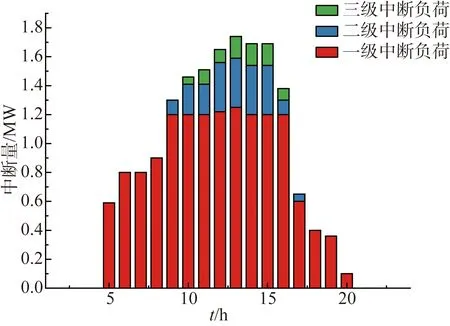
图8 可中断负荷响应情况分析

4.3.3 微网参与日前和实时市场分析

日前和实时市场的交易电量如图9所示，图中正值表示微网向上级电网出售电量，负值表示微网从上级电网购买电量。

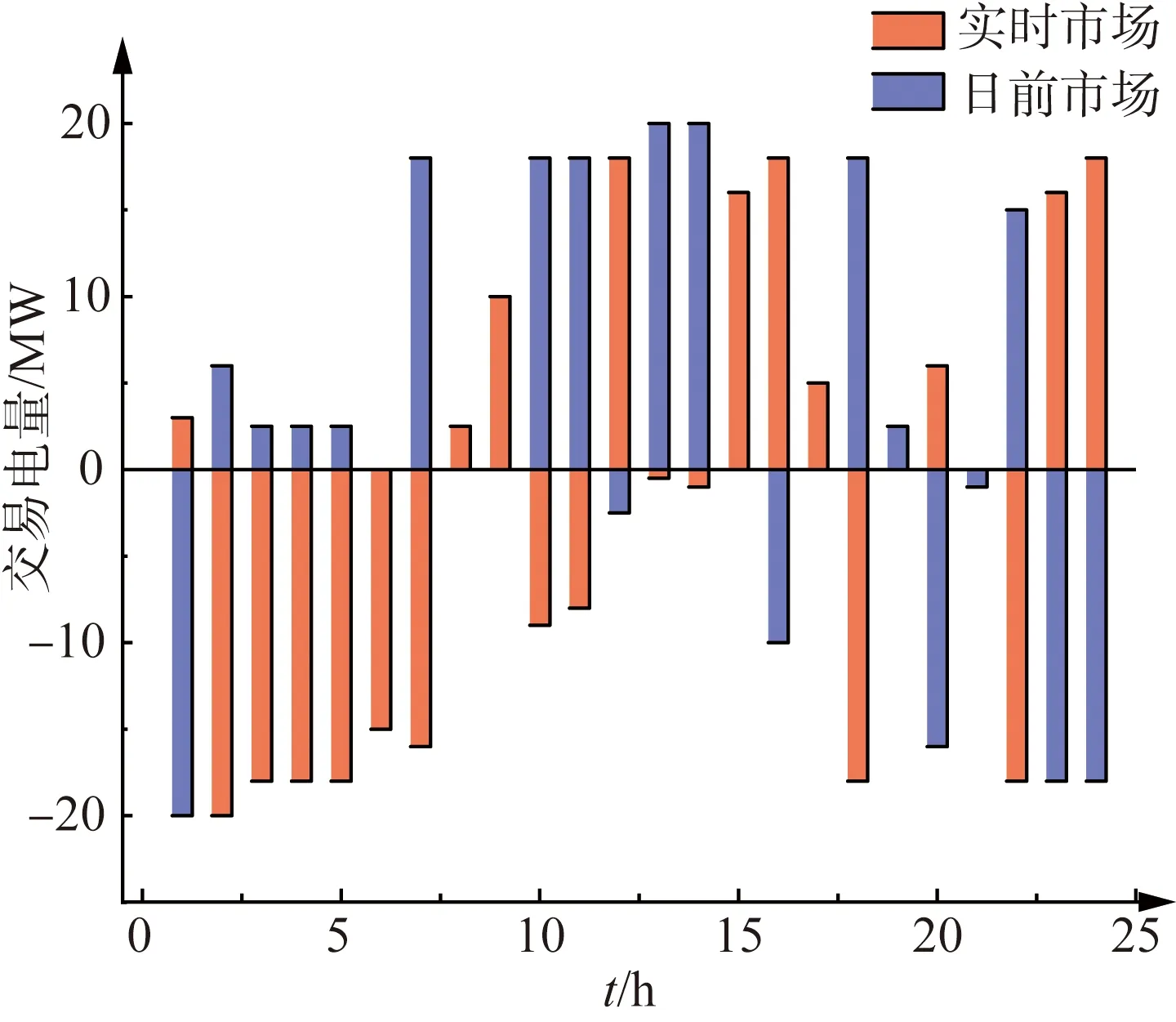
图9 微网与上级电网电量交易情况

本文所建立的模型考虑微网同时参与日前市场和实时市场，然而，考虑到光伏出力的不确定性，实时市场所作的决策需要根据日内实时的光伏以及负荷的实际情况进行调整，从而需要从实时市场进行电量的购入与出售，保证微网各功率单元保持平衡，避免遭受不平衡惩罚。

从图9中可以看出，微网在日前市场与实时市场的购售电策略有所区别。由于日前市场的购售电量是第一阶段的决策变量，是未考虑光伏、市场电价不确定性的前提下对燃气轮机、储能等分布式电源的出力进行决策，而实时市场是在考虑光伏、市场电价不确定性的前提下，针对最恶劣的光伏场景进行决策，因此，两个阶段的市场购售电量有所区别。从图中也可以看到，0-8时段，微网向日前市场出售电量，而选择向实时市场购买电量。9-16时段，由于市场电价较高，此时段微网在日前市场以及实时市场，均以向电力市场出售电量为主，实时市场部分时段出现从市场购电的情形，主要原因是考虑了最恶劣场光伏出力场景，在10、11时段，本该出力较高的光伏机组却因为短暂的天气因素导致出力偏低，微网难以满足实际负荷供给需求，故作出向实时市场购买电量的决策。从这个角度来看，本文同时考虑微网参与日前市场以及实时市场，能够降低微网的运行风险，提高微网的收益。

5 结论

本文结构考虑了微网同时参与日前市场、实时市场以及碳交易市场，通过随机规划法处理市场电价的波动性，并运用两阶段鲁棒优化法处理光伏出力的不确定性，建立了微网两阶段鲁棒优化模型，并基于恶劣场景辨别法，将原max-min-max问题分解为主问题和子问题进行迭代求解。主问题主要用于求解恶劣场景集合下的微网单层优化问题，子问题用来辨别所有光伏出力场景下的最恶劣场景。最后通过算例测试，得出结论如下。

1)恶劣场景辨别法极大地削减了光伏场景数量，减少了计算时间，并且对于场景数量较多的计算模型，该方法计算时间增长缓慢，可适用于大规模场景下的两阶段鲁棒优化模型的求解。

2)恶劣场景集外的场景对于最终的计算结果没有影响，即恶劣场景集可以替代原始大规模的不确定场景集，且可以完整地保留原场景集的不确定信息。

3)微网同时参与多种市场可以一定程度上提高利润，实现微网灵活调度要求。

随着售电侧的进一步开放，未来将会有越来越多的需求响应资源涌入电力市场，因此，未来微网负荷侧的需求响应资源类型将包含可中断、可转移负荷以及虚拟储能特性负荷(如电动汽车)，本文目前只对可中断负荷进行建模分析，后续将对此开展进一步的研究工作。