低风压架空导线的风致响应特性
2021-06-16唐力刘磊李斌柯子桓黎小林王国利
唐力,刘磊,李斌,柯子桓,黎小林,王国利
(1. 南方电网科学研究院,广州 510663;2.中国南方电网有限责任公司,广州510663)
0 引言
防风设计是保障输电线路安全运行的重要因素,导线承受的风载荷对杆塔的强度设计影响较大。为了降低导线所受风载荷,新型导线——低风压导线被研发出来以降低导线本体风阻系数[1]。目前,低风压导线的工程实际应用较少,开展低风压导线的抗风性能研究,对低风压导线的推广使用有重要指导意义。
低风压导线由于其特殊的表面结构,具有降低本体风阻系数的功能[1 - 4]。目前,低风压导线的表面结构形式各异,针对低风压导线的研究集中在风阻特性、力学性能、技术经济等方面[5 - 11]。其中风阻特性研究主要开展低风压导线风洞试验和数值仿真,对比分析其风阻系数与常规导线差别,研究分裂系数对风阻特性影响[5 - 9]。力学性能研究主要涉及低风压导线结构稳定性、放线跳股等问题[10]。技术经济性研究主要分析低风压导线在输送容量、电磁环境、电气性能、投资经济等方面与常规导线的差别[11]。国内现行规范有关导线风荷载计算风阻系数取固定值,没有区分导线的类别[12]。针对导线的气动特性的研究多集中在通过风洞试验和仿真研究覆冰、分裂数、风速、型号等因素对导线体型系数、舞动和风偏等特性的影响,并没有涉及风载荷下低风压导线的静力特性和动力响应研究[12 - 21]。由于特殊的表面结构,低风压导线与常规导线的风致动力响应差别也尚不清楚。开展低风压导线风载荷下静力和动力响应分析,有助于全面评估低风压导线的抗风性能,指导低风压导线的工程应用。
本文针对低风压导线的抗风性能开展了相同半径的低风压导线和常规钢芯铝绞线的风洞试验,得到了导线的风阻系数。利用试验得到的风阻系数,基于“悬链线方程”和风荷载下导线档距中点的风致动力响应模型,对比分析了低风压导线和常规导线的在稳恒风和脉动风下的力学特性。
1 风洞试验
由于雷诺数效应,输电导线的风阻系数与风速相关。因此,开展风洞试验测试半径相同的低风压导线和常规钢芯铝绞线风阻系数,获得其风阻系数随风速变化的公式。
1.1 试验装置和试品
本文试验在同济大学土木工程防灾国家重点实验室TJ- 2大气边界层风洞实验室进行。该风洞试验段尺寸为3 m×2.5 m×15 m,能够产生2 ~68 m/s的连续风速。
为保障试验导线直径相同,采用铝棒制作模型导线,模型导线表面结构分别与实际常规钢芯铝绞线和低风压导线表面结构一致,模型线直径为33.4 mm,导线截面示意图如图1所示。试品布置实物图如图2所示。

图1 架空导线试品截面示意图

图2 试品布置图
1.2 试验方法和内容
考虑沿海地区输电线路的设计风速和风洞性能,设置了7个风速:10、15、20、25、30、35、和40 m/s。试验测量了导线在上述7个风速下所受的风力,然后由式(1)给出导线的整体阻力系数。
(1)
式中:F为试验每个风速下所测得的导线所受阻力均值;ρ为空气密度,kg/m3;V为风速,m/s;L为模型导线长度,m;d为导线外径,m。
1.3 试验结果及分析
对试验得到的测试导线的风阻系数采用最小二乘法,利用三次多项式进行拟合,获得低风压导线和常规钢芯铝绞线风阻系数与风速的拟合曲线,如图3所示,表达式分别如式(2)—(3)所示,拟合优度均为0.96。

图3 架空导线风阻系数
Cd=8-5V3-5.7-3V2+0.104 19V+0.555 71
(2)
Cg=-6.444 4-5V3+5.63-3V2-0.154 13V+2.137 9
(3)
式中:Cd为低风压导线风阻系数;Cg为常规钢芯铝绞线风阻系数;V为风速,m/s。
由图3可知,低风压导线和常规钢芯铝绞线的风阻系数随风速的增大先减小后小幅增大且趋于平稳,符合导线风阻系数雷诺数效应影响规律,即存在一个临界雷诺数,使得导线风阻系数减小后趋于平稳[21]。低风压导线在20~30 m/s风速区间风阻系数随风速的增加减少较快,常规钢芯铝绞线在10~15 m/s风速区间风阻系数随风速的增加减少较快,最后两者风阻系数分别稳定在0.70和0.86左右。当风速大于25 m/s后,低风压导线风阻系数较常规钢芯铝绞线小17.65%左右,而在25 m/s以下风速区,低风压导线风阻系数大于常规钢芯铝绞线。在高风速区,低风压导线才能发挥降低风阻系数的作用。
2 稳恒风荷载下低风压导线特性分析
根据上节风洞试验得到的导线风阻系数,结合“悬链线方程”,计算导线风偏角和最大弧垂,对比分析低风压导线和常规导线静力特性。
2.1 计算方法及参数
悬链线方程如式(4)所示。
(4)
(5)
式中:σ0为导线最低点水平应力;γ为综合比载,是自重比载与风压比载的矢量和,如式(5)所示;γ1为自重比载;γ2为风压比载;θ为风速垂直于导线轴向的分量与x轴的夹角;C1、C2为积分常数,根据所取坐标原点的位置及边界条件而定。
为分析低风压导线和常规导线静力特性的区别,考虑到二者只是表面结构存在差异,结合本次试验导线型号,做如下假设:计算线路档距为450 m,高差为0 m,弧垂最低点运行应力为57 MPa,温度为20 ℃,导线自重均为20 N/m。
2.2 计算结果分析
当风向角为0 °时,计算得到的导线风偏角与风速的关系如图4所示。
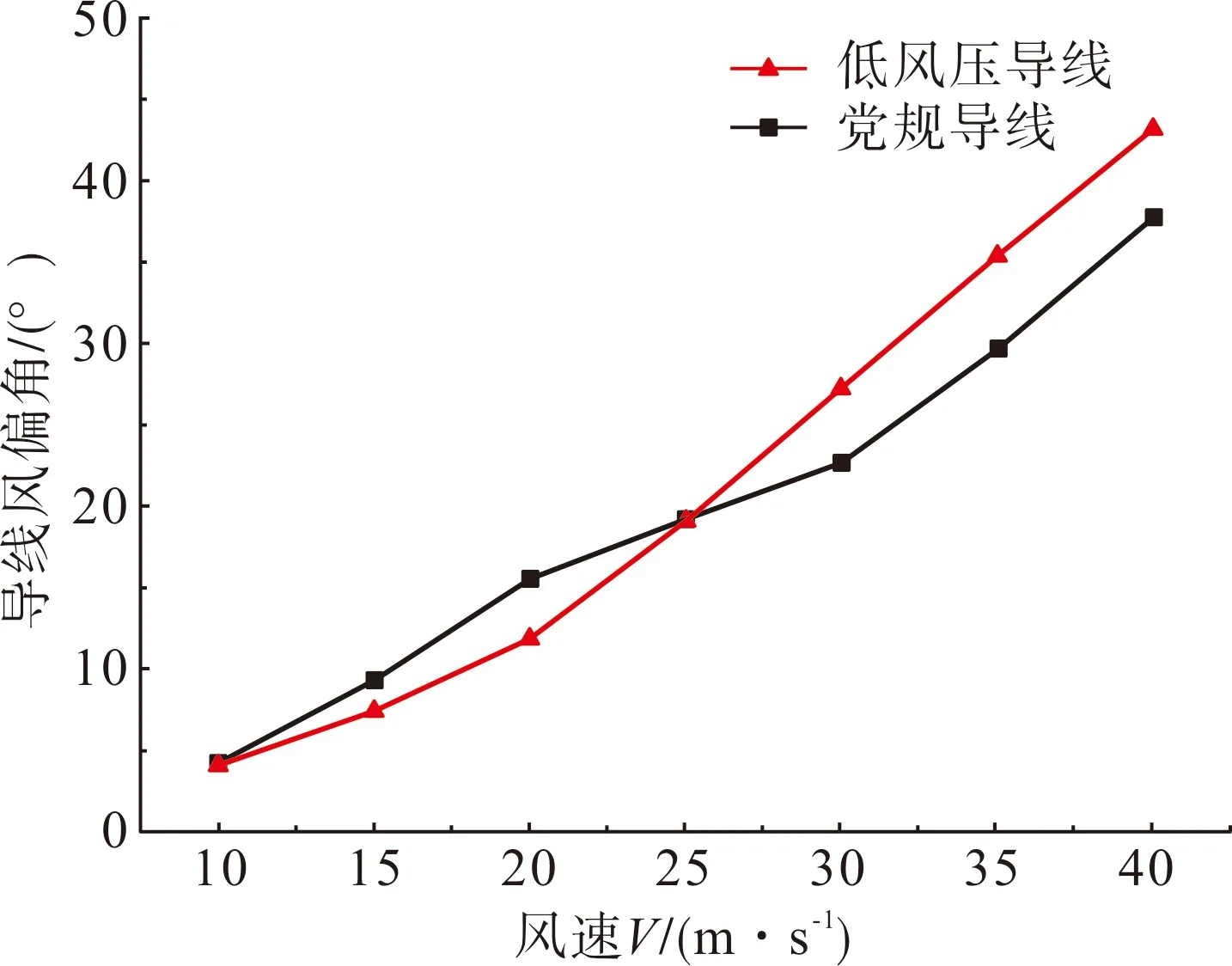
图4 架空导线风偏角
由图4可知,2种导线风偏角随风速的变化规律与风阻系数随风速变化规律相似。低风压导线在高风速区(>25 m/s)由于风阻系数较小,其风偏角较常规钢芯铝绞线小16.5%左右。在20 m/s风速下,低风压导线由于风阻系数较大,其风偏角较常规钢芯铝绞线大31.9%。
当风攻角分别为+30 °和-30 °时,计算得到的导线最大弧垂与风速的关系如图5所示。可以看出,当风攻角为-30 °时,2种导线最大弧垂随风速变化规律与风阻系数随风速变化规律相似。当风攻角为+30 °时,2种导线最大弧垂随风速变化较小。由式(5)可知综合比载是自重比载与风压比载的矢量和,所以风攻角不同时,常规钢芯铝绞线和低风压导线最大弧垂随风速变化规律不同。

图5 架空导线最大弧垂
3 脉动风荷载下低风压导线动力响应分析
实际线路中导线所受风载荷是脉动的,开展低风压导线脉动风荷载下低风压导线动力响应分析能更准确评估导线防风性能,本节建立了架空导线的档距中点风致动力响应模型,分析了脉动风荷载下低风压导线位移和频率特性。
3.1 计算方法及参数
为分析脉动风载荷下低风压导线与常规钢芯铝绞线动力响应的差别,假设导线两端固定,不受相邻档距的影响,导线张力和风载荷沿档保持不变,考虑导线的重力、风载荷、阻尼力、张力和惯性力,建立导线档距中点在脉动风荷载下运动的力学模型,控制方程如式(6)所示[22 - 23]。
(6)
式中:Fy为风载荷垂直方向的分量,N;Fx为风载荷水平方向的分量,N;m为单位长度导线质量,kg;Cy、Cx分别为垂直和水平方向的阻尼系数,N·s/m;x、y、x′、y′、x″、y″分别为导线在水平和垂直方向的不同位移,kx、ky分别为导线刚性在水平和垂直方向产生的力系数,由导线水平张力、线路档距计算获得。
本文模拟的风速时程由平均风和脉动风两部分构成,采用Davenport水平脉动风速谱模拟脉动风,取地面粗糙系数k为0.002 15,考虑到本文开展风阻试验的风速范围,取10 m高度处的风速为25 m/s,施加脉动风的风速时程如图6所示。

图6 风速时程图
针对本文涉及的常规钢芯铝绞线和低风压导线,计算了脉动风荷载下导线档距中点的位移时程,其中重力加速度取9.8 m/s2,档距取450 m,导线最低点运行张力为25%计算拉断力,垂直和水平方向的阻尼系数均为0.005,空气密度1.2 kg/m3,风攻角为30 °。考虑到导线风阻系数与风速有关,采用1.3节拟合试验数据得到的导线风阻系数公式。
3.2 计算结果分析
计算得到的低风压导线和常规钢芯铝绞线档距中点x和y方向位移时程图分别如图7和8所示。低风压导线和常规钢芯铝绞线档距中点的位移轨迹图如图9所示。

图7 架空导线x方向位移时程图

图8 架空导线y方向位移时程图
由图9可知,低风压导线的振动幅值小于常规钢芯铝绞线,x和y方向振动幅值分别比常规钢芯铝绞线小约2.5 m和1.1 m。由风洞试验可知,低风压导线在25~40 m/s风速区的风阻系数更小,因此低风压导线在平均风速为25 m/s的脉动风作用下的振动幅值相对常规钢芯铝绞线导线更小。
对低风压导线和常规钢芯铝绞线位移数据进行傅里叶变换,得到低风压导线和和常规钢芯铝绞线档距中点x和y方向位移频谱图如图10—11所示。

图10 常规钢芯铝绞线位移频谱图

图11 低风压架空导线位移频谱图
由图10—11可知,2种导线x和y方向的振动频谱曲线都是相似的,且频率主要集中在低频段,在0.19 Hz处有一波峰,但低风压导线频率的幅值要小于常规钢芯铝绞线。
4 结论
本文对低风压架空导线和常规钢芯铝绞线开展了风洞试验,研究了不同风速下两种导线风偏角和弧垂的差别,计算了两种导线在脉动风作用下动态响应的差别,得到结论如下。
1)导线风阻系数随风速的增大先减小后趋于平稳,低风压导线在25 m/s以上高风速区风阻系数小于半径相同的常规钢芯铝绞线。
2)在高风速区相同稳恒风荷载激励下,低风压导线风偏角小于半径相同的常规钢芯铝绞线;在相同脉动风荷载激励下,低风压导线与普通钢芯铝绞线的档距中点位移轨迹和频谱相似,但低风压导线振动幅值较小。
3)低风压导线在高风速区才能发挥降低所受风载荷的作用,可为提高输电线路抗强风能力提供新途径。
