Z地区天然气管网平衡差影响因素分析与天然气需求短期预测

李光越 王泽鑫 于文广 李国军 石咏衡 张博越

国家管网生产经营本部（油气调控中心）

“十四五”报告中指出要加快推动绿色低碳发展战略，推进能源清洁化、利用高效化进程，制定2030 年前碳排放量峰值方案[1]。天然气因清洁高效、经济效益高等优点，一直是我国进一步实现低碳发展的重要选择[2]，天然气管道建设也迎来新的高峰。近年来中俄东线北段、中俄东线中段、闽粤支干线、青宁管线等相继完成投产工作，国内天然气消费量也随之大幅度增加。《中国天然气高质量发展白皮书（2020）》指出极端天气下我国应急调峰能力仍显不足，储气库等调峰设施可调配的天然气量低于世界平均水平[3]。兼顾管网安全运行与供气可靠性问题对管网调度运行提出新的考验，而管网进销平衡控制是解决该问题的关键。

天然气进销平衡差直接影响的是管网管存[4]，管存过高直接引发整条管线平均压力过高，增加运行风险；而管存过低，则无法满足用户供气压力，增大管线运行摩阻，增加管网能耗损失。基于此开展对影响Z地区天然气进销平衡差的因素分析，建立预测区域进销气量模型。

为能够准确确定某区域天然气消费量的预测模型，相关学者已经展开了多方面、多角度的研究工作。基本上将预测模型划分为某时间段区域消费总量预测以及短期天然气消费量预测两个层次[5]，其中关于消费总量的预测研究，多集中在全国或省级等范围的预测。通过宏观预测可以帮助相关部门对我国能源结构调整、天然气管网以及配套设施建设提供理论参考，对能源经济的宏观调控提供便利[6]。但这种预测对区域管网的日常生产指导意义较弱、针对性较差、缺少实效性，因此建立区域短期天然气消费模型是非常必要的。

天然气短期需求量预测的研究表明，天然气短期需求量呈现明显的周期性与规律性，这种周期性波动规律的准确判断需要专业人员具备丰富的实践与理论储备[7]，同时这种规律与区域电力负荷的波动规律基本相似，因此可以借鉴电力负荷预测方法来研究天然气短期需求规律。郝迎鹏[5]提出天然气短期需求是控制管网运行、制定管网调度运行计划的依据，认为天气参数、节假日、天然气价格等都是天然气短期预测重要指数，并对北京市与其他地区实际需求量进行比较，验证其观点的准确性。李兰兰[8]利用分解重构向量机方法，以郑州燃气管网过去168 h 负荷数据作为输入参数，预测了接下来24 h天然气的需求量，并通过结果证明该预测方法优于传统BP 网络以及最小二乘支持向量机方法。彭芳[9]等考虑某市日最高气温、日最低气温、平均气温、相对湿度、日期类型等因素，分别建立回归分析、BP神经网络短期预测模型，结果显示BP神经网络模型预测结果更接近实际值。

1 管网平衡差影响因素分析

1.1 影响因素确定

Z地区在役一级天然气管道建设里程长，下游分输用户类型齐全，配有调峰功能的LNG、储气库等设施。随2018 年底自动分输工程的推进，积累了较为丰富的进销分输动态资料，具备对天然气管网进销平衡差指标进行精细评价的基础。本文所探究的平衡输差是指每日上午8点Z 区域所结算的进气量与销气量的差。

收集Z 地区天然气管道近3 年每日进销气量的历史数据，为全面建立预估模型，保留因作业、异常事故等因素造成的突变数据。绘制管网每日进销平衡差以及平衡偏差率变化趋势（图1），其中管网当日平衡偏差率为当日进销平衡差与当日进气量的比值。

由图1可知，平衡差的存在是不可避免的，无法保证管网进销气一直处于平衡状态。平衡差的值处于波动状态且周期性并不明显，因此，从宏观上直接分析进销平衡差的变化规律是不可行的，为准确掌握平衡差变化趋势，指导天然气管网生产运行，还需进一步分析平衡差的影响因素。

图1 近三年Z地区天然气管网进销平衡差以及平衡偏差率变化趋势Fig.1 Trend of the balance difference between input and output and the balance deviation rate of natural gas pipeline network in Z area in recent three years

1.2 影响关系确定

1.2.1 节假日对管网平衡差的影响

为了探究节假日对管网平衡差的影响，绘制2017年4月1日—2020年3月31日全年平衡差随时间分布趋势图（图2），同时用红色标出节假日期间管网的平衡差。通过统计，2017—2019 年在节假日时平衡差增长概率分别为54.9%、51.0%、55.1%，且有29.4%、26.5%、34.7%概率达到近期平衡差的极大值，说明节假日对于管网平衡差影响较大。

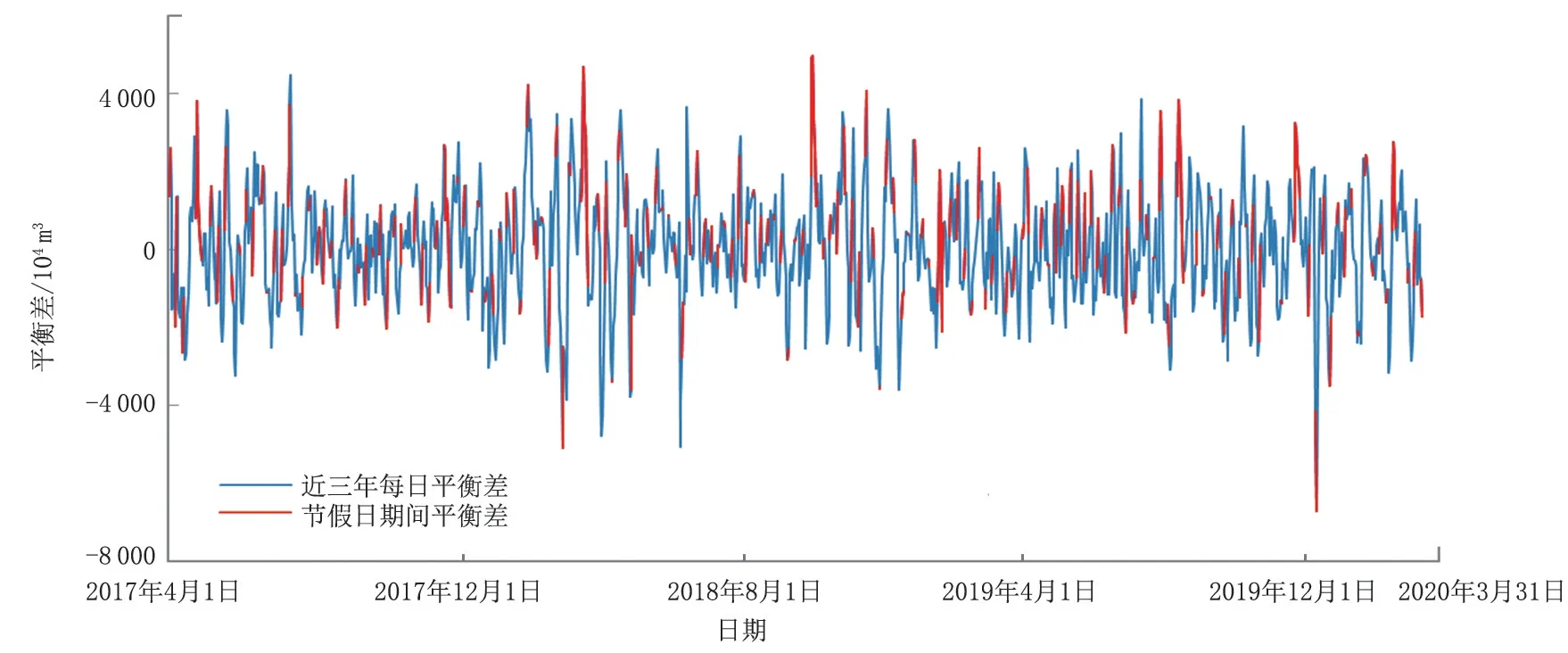
图2 2017—2019全年管网进销平衡差随时间分布趋势图（节假日）Fig.2 Distribution trend of balance difference between input and output with time from 2017 to 2019（Holidays）

1.2.2 温度对于管网平衡差的影响

通过气象网站查阅2017 年1 月1 日至2020 年3月31日Z地区管道途径城市每天历史温度值，平均后将其定义为Z地区每天的平均温度值。

2017 年1 月1 日至2020 年3 月31 日Z 地区天然气管网进销气与全国平均气温的分布趋势图见图3。从整体上来看，在这段时间内，管网销气与平均气温均呈周期性变化，且两者有负相关性，随年平均气温降低管网的销气量升高，随平均气温升高管网销气量呈先降后稳的变化，这是因为每年4-10 月随着气温回升，北方地区进入非供暖季，使得Z地区用户用气量趋于一个相对稳定的状态。

图3 2017—2019全年Z地区管网进销气量随时间分布趋势图（气温）Fig.3 Distribution trend of input and output gas volume with time in Z area from 2017 to 2019（Temperature）

从局部上看，在2017年1月1日至2020年3月31 日，每年的销气量都在1 月份前后达到极大值，且该值呈逐年递增趋势，从2017 年39 791×104m3增加至2020年53 920×104m3，其中2017—2018年管网销气增长幅度最大，增长率达到14.8%。

1.3 各因素对管网平衡差的影响

通过分析确定了影响Z地区管网进销平衡差的因素，包括季节、节假日、温度等，但各因素对于管网进销平衡差的影响程度无法判定。针对此问题，采用方差分析法对各参数进行分析，综合评价出各因素对管网进销平衡差的影响程度。

方差分析是一种能够有效判断某因素对于结果有无影响以及影响大小的方法。该方法的基本原理是根据实际的数据结构将总偏差平方和分解为两部分，一部分反应试验误差造成的差异，另一部分反应因素水平误差造成的差异，运用F检验法判断因素是否对结果呈显著性影响，进行最后的定量分析判断[10]。2017—2019年不同因素下进销平衡差平均值见表1。

表1 2017—2019年不同因素下进销平衡差的平均值Tab.1 Average value of the balance difference between input and output under different factors from 2017 to 2019

首先对近三年不同因素下进销平衡差进行方差分析，依据方差分析法原理，通过计算得出数据修正项RT、数据总的偏差平方ST和数据总的自由度fT。

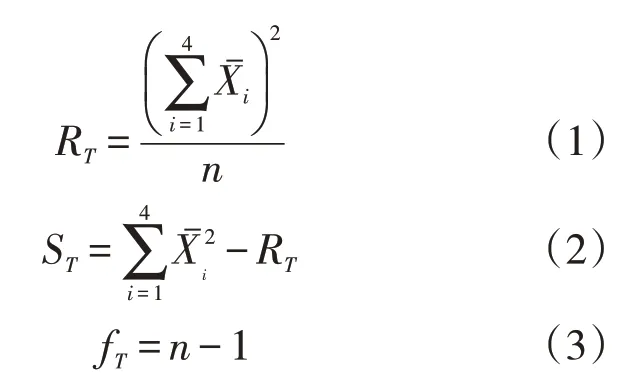
不同因素的数据组内偏差平方和Si、组内数据均方差Vi、组内数据自由度fi的计算公式为

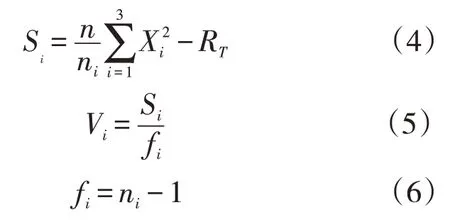
式中：Xi为不同因素组内数据数值；ni为不同因素组内数据个数。

不同因素的数据组间数据偏差平方和SE计算公式为

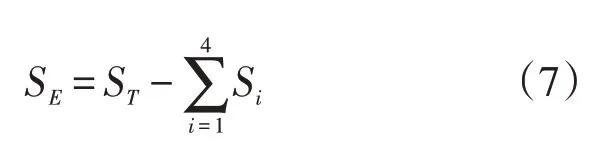
方差分析结果如表2所示。表2中α、F、Fα是方差分析F检验法中常用的符号，其中α为显著性水平，Fα为根据数据自由度以及自由变量数的值，通过查阅不同显著水平下F分布检验表后所得的结果[11]。通过与α=0.01，α=0.05 水平下的对比得出，夏季、冬季、节假日、非节假日因素对管网进销平衡差有显著影响，该结果与上述通过图表直观分析所得结论相同。

表2 进销平衡差的方差分析Tab.2 Variance analysis of the balance difference between input and output

为探究各因素间对管网进销平衡差影响程度的大小，采用q检验法，对不同因素的显著性水平进行两两比较，结果见表3、表4。

表3 四种因素下管网平均进销平衡差排序Tab.3 Ranking of average balance difference between input and output of pipe network under four factors

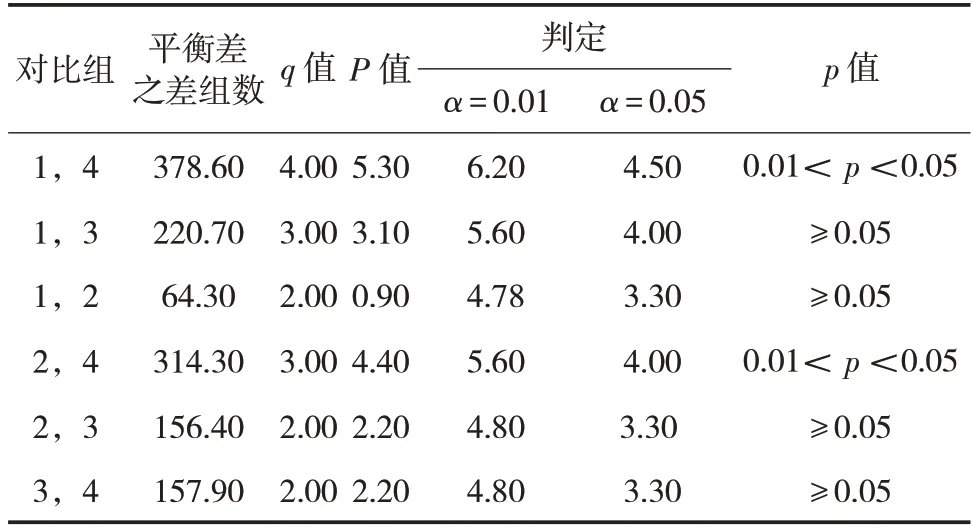
表4 四组均数对比（q检验法）Tab.4 Comparison of four groups of mean（q test method）

表中P值可以通过α=0.01，α=0.05 显著条件下q的界值表查找，而q值的计算公式为

由表4可知，在α=0.01，α=0.05 水平上，第一组与第四组数，第二组与第四组数据存在0.01＜p＜0.05 关系，其余组间存在p≥0.05 的关系，即说明冬季与夏季，节假日与夏季的平衡差均值有显著差异性，其余组间则无显著差异性。该结论再一次证实冬季、节假日管网进销平衡差的波动性。

2 管网销气量神经网络预测模型

2.1 预测模型建立

2.1.1 BP神经网络模型算法

BP 神经网络模型是一种以误差验证结果为逆传播导向的多层前馈型神经网络模型[12]。该模型模拟大脑信息处理逻辑对数据进行处理，通过大量反复的训练学习，建立一种高效的容错反馈学习机制，揭示数据间非线性映射关系[13]。该算法拓扑组成包括输入层、隐藏层、输出层，其中隐藏层可以是多层的，但一般不超过3 层。利用极小化函数（激活函数）建立输入、输出层间的映射关系，根据所得网络误差值反向传播方式反复调整阈值和权值，而从获得以误差最小化为导向的神经网络参数配置[14-15]。

2.1.2 Elman神经网络模型算法

Elman 神经网络模型也是一种前馈型神经网络模型，算法拓扑组成包括输入层、隐藏层、承接层、输出层，相当于在传统BP 神经网络模型的隐藏层中增加了承接层[16]。Elman 神经网络实现的原理是：参数作为样本通过输入层进入神经网络，通过激活函数建立输入层与隐藏层间的非线性关系，承接层接收隐藏层前一时刻输出值后，作为一步延时算子再一次返回隐藏层的输入，最后通过线性加权得出输出层结果[17]。

2.1.3 RBF神经网络模型算法

RBF 神经网络模型是一种径向基函数神经网络，算法拓扑组成包括输入层、隐藏层、输出层，其中隐藏层为单层结构[18]。输入层通过径向基函数建立与隐藏层的非线性关系，而隐藏层通过线性加权求和建立与输出层关系得出输出结果[19]。其中基函数通常为一种高斯函数，通过对数据中心和基宽参数的选择，实现RBF 神经网络模型隐藏层与输入层间的数学联系。与传统BP 神经网络模型相比，RBF神经网络具有学习速度快，处理数据泛化能力强，同时能够良好地避免局部极小值的问题[20]。

2.2 销气量短期预测模型数据处理

2.2.1 预测模型训练样本采集

样本采集取自Z地区2017年1月1日至2020年3月31日管网进销气量的数据库。考虑到进销气量每年4～10 月间波动较小，检验模型合理与否存在偶然性，因此把2017年年1月1日至2020年2月29日数据样本为训练数据，2020年3月1日至31日作为测试样本，来验证该短期预测模型的准确性。

选取待预测时间()d前三天（d-3）、前两天（d-2）前一天（d-1）的管网进气量、销气量、平均气温、最高气温、最低气温以及待预测时间当日日期类型，16 个维度的矩阵作为输入数据，模型输出值为待预测时间当日的管网销气量。

2.2.2 样本数据归一化处理

（1）进销气量与温度数据归一化。训练样本包括Z地区进气量、销气量、气候温度、日期类型等参数，各参数数量级别、量纲单位存在差异，使得训练结果误差增大。为避免因训练样本数据量纲差异造成的影响，需要对所有输入、输出数据进行归一化处理，将各参数归换算至[-1，1]区间。换算公式为

式中：x′为归一化后数据；X为归一化前数据；xmax、xmin分别为X数据参数中的最大值与最小值。

（2）日期的归一化。根据影响管网平衡差因素的方差分析，考虑日期对平衡差的影响程度，将其分类为工作日（周一至周五）、双休日（周六日）、节假日（元旦、春节、清明、劳动、端午、中秋、国庆）三类。为进行数据归一化处理，定义工作日为0，双休日为1，重大节假日对平衡输差影响过大，加入到训练数据中会影响预测模型对非重大节假日管网销气量预测的准确性，因此在本部分将重大节日数据参数剔除，后续将专门建立神经网络节假日短期预测模型。

2.3 神经网络预测模型精度的评定

预测模型精度通过平均相对误差以及均方根误差作为评判标准，公式如下

式中：δ、MAPE、RMSE分别为相对误差，平均相对误差和均方根误差，%；yi为通过神经网络计算预测出i天的管网销气量，104m3；Yi为待预测时间i天管网的实际销气量，104m3；a为预测样本数量；N为求均值样本数量。

2.4 神经网络短期预测模型结果分析

通过上述过程建立的神经网络预测模型对2020年3月1日至2020年3月31日Z地区天然气管网销气量进行了预测。将预测值与实际值进行对比发现，三种神经网络模型都能够较好地预测Z地区天然气销量，所得平均相对误差最分别为1.95%、1.51%、1.45%，均方根误差分别为781.34×104m3、703.65×104m3、655.31×104m3，其中RBF 神经网络能更准确地预测Z 地区3 月份天然气的需求量。

由图4可知，三种神经网络预测模型所产生的误差均在-4%～4%之间。其中BP、Elman、RBF 神经网络预测相对误差分别在3月20日、3月3日、3月31 日达到极值3.67%、-4.00%、-3.77%，说明虽然传统BP 神经网络预测平均相对误差较大，但预测结果偏离程度较小。三种神经网络模型所得相对误差为正值的比例为80.65%，41.94%，54.84%，说明BP 神经网络预测Z 地区天然气需求值易大于实际值，Elman 神经网络预测Z 地区天然气需求值易小于实际值。

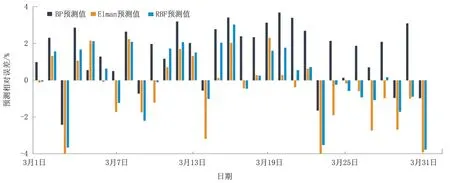
图4 神经网络预测相对误差柱状图Fig.4 Column of relative error in neural network prediction

通过图5对比发现，三种神经网络预测值与实际值的走势基本吻合，能够准确地预测Z 地区3月份天然气销气量的变化规律。同时可以观察出RBF神经网络预测曲线与实际值十分接近，精度要明显高于其他两种预测模型，但局部存在偏离程度大的情况，例如3 月20 日和21 日RBF 预测模型预测精度就要低于另外两种模型。

图5 神经网络预测值与实际值对比曲线图Fig.5 Comparison curve of neural network predicted value and actual value

2.5 神经网络预测重大节日管网销气的模型

节假日会影响用户的用气规律，管网整体销气量一般会比平时有所降低。2020 年春节期间受疫情影响，全国多地管存接近应急高水平。为做好管网运行调整，控制管道管存在合理范围内，建立重大节日管网销气模型是十分必要的。在上述三种神经网络训练样本中加入2017—2020 年重大节日（元旦、春节、清明、劳动、端午、中秋、国庆）管网进销气量、气温等数据参数，根据神经网络构建思想，建立模型来预测重大节日期间管网销气量。

根据方差分析可知，冬季、节假日均是影响管网进销气造成波动的参数，为验证神经网络对于重大节日管网预测的准确性，对2019 年和2020 年冬季元旦、春节假日期间管网销气进行预测，并与实际值进行对比发现，三种模型差距较为明显，所得到的平均相对误差分别为2.47%、2.12%、1.95%，均方根误差分别为1 184.46×104m3、774.68×104m3、630.67×104m3。其中Elman、RBF神经网络模型预测结果较好，能够较为准确地预测重大节日下Z地区管网销气量，而传统BP 神经网络模型预测结果偏离实际天然气消费量较大。同时重大节假日下预测结果的误差值明显大于非节假日下短期预测模型的误差值，证明节假日天然气销量预测难度较大，需建立重大节假日预测模型。

从图6可知，三种神经网络预测模型所产生的误差均在-4%～6%之间，其中BP、Elman、RBF 神经网络预测相对误差分别在2019年2月4日、2020年1 月26 日、2020 年1 月1 日达到极值-5.68%、4.99%、5.34%，误差波动极值明显大于非重大节假日模型误差波动程度。由图7对比发现，三种神经网络对于预测值与实际值走势基本吻合，能够准确反应Z 地区2019 年至2020 年天然气销气量重大节日天然气需求的变化规律。同时可以观察出RBF神经网络预测曲线与实际值最为接近，精度要明显高于其他两种预测模型，但局部存在偏离程度大的情况，例如2020 年元旦RBF 预测模型预测精度要低于另外两种模型。

图6 重大节日神经网络预测相对误差柱状图Fig.6 Column of relative error in neural network prediction on major holidays

图7 重大节日神经网络预测值与实际值对比曲线图Fig.7 Comparison curve of neural network predicted value and actual value on major holidays

3 结论

（1）针对Z地区天然气管网进销特征，结合近3 年管网进销平衡差动态资料，将季节、节假日、气温等因素与管网进销气量、平衡差等动态数据相结合，研究影响管网平衡差的主要因素。并采用方差分析法对各影响因素进行综合评价，量化分析各因素对管网平衡差的影响程度。结果表明冬季（供暖季）、节假日对管网进销平衡差有显著的影响。

（2）以进气量、销气量、气温、日期类型为输入参数分别建立传统BP、Elman、RBF神经网络天然气消费量短期预测模型。通过与实际销气量对比，得出平均相对误差分别为1.95%、1.51%、1.45%，均方根误差分别为781.34 × 104、703.65×104、655.31×104m3。相比其他两种模型，RBF神经网络预测值更加贴近实际销气量，具有良好的预测能力，能够准确预测短期时间内管网日销气量。

（3）在已建短期神经网络模型基础上，加入近3年重大节日相关参数，建立RBF神经网络重大节日期间管网销气量预测模型，通过与实际值对比发现，模型所得误差值稍大于非节假日下的预测模型，且误差在合理的范围之内，无论是从相对误差大小还是与波动范围角度来看，该模型都能较为准确地预测重大节日下管网销气量，为Z地区管网调度运行、工况调整提供数据支持。