一种多部位损伤全寿命分析的工程方法

2021-06-16奚蔚李强沈培良何瑞杨刚刘世杰

航空学报 2021年5期

奚蔚,李强,沈培良,何瑞,杨刚,刘世杰

1.中国商飞上海飞机设计研究院机体集成部,上海 201210

2.中国商飞上海飞机制造有限公司复合材料中心,上海 201324

近年来,飞机老龄化问题日趋严重,它涉及很多方面,广布疲劳损伤是其中的重点和难点之一。FAR25-132修正案§25.571条款“结构损伤容限和疲劳评定”要求必须建立一个有效性限制,在有效性限制内,飞机结构不允许发生广布疲劳损伤[1]。研究结构的广布疲劳损伤需要确定3个方面的关键问题：多裂纹萌生、多裂纹扩展以及多裂纹结构失效分析[2-4]。本文就这3个问题进行了研究。

对多裂纹萌生问题,薛景川和弓云昭[5]提出了一种预估结构初始广布疲劳损伤发生的概率模型,该模型将结构简化成一个并串联系统,并推导出相应的计算公式。王传胜等[6]给出了一种利用已有单细节结构试验结果定量计算飞机结构发生多部位损伤可能性的方法,该方法认为当多细节结构中有2个或2个以上细节萌生裂纹时,结构发生多部位损伤。Zhang等[7]从单细节结构裂纹萌生寿命概率分布出发,给出了多细节结构萌生任意多条裂纹概率的数值计算公式。本文通过研究多细节结构中裂纹萌生的机理,给出了多细节结构中依次出现的各条裂纹的萌生寿命概率分布的解析表达式,使得多裂纹萌生寿命概率分布的概念更加清晰,计算过程更加简单,结果更加准确。

对多裂纹扩展问题,它的关键是应力强度因子的计算。Cartwright和Rooke[8]提出了多裂纹应力强度因子求解的组合法,组合法是利用叠加原理和约束替代原理建立的一种工程近似计算方法,它将复杂情况分解成若干简单情况的组合。倪惠玲[9]应用这一方法对多处损伤的特性进行了初步研究。Moukawsher等[10]用修正的Kamei和Yokobori交互作用因子来考虑相邻裂纹对应力强度因子的影响。上述研究方法只能解决有限情况下特定分布的裂纹问题,对于任意分布的多裂纹问题,有限元法无疑是工程实际中常用的方法[11],它能够求解复杂几何边界条件或复杂载荷传递情况的应力强度因子。另外,随着裂纹扩展,不断快速动态更新裂尖应力强度因子也是一个难题。本文先通过有限元方法计算出多裂纹指定长度组合下的应力强度因子,然后引入响应面法,定量地建立裂纹长度与应力强度因子之间的函数关系,减少有限元迭代计算工作量,解决了多裂纹应力强度因子的快速动态计算问题,兼顾了计算精度和效率。

对多裂纹结构失效问题,Swift[12]在窄板剩余强度试验中发现,由于受到韧带屈服的限制,窄板的失效由净截面屈服准则控制。由于各裂纹之间的相互作用,多裂纹结构中的裂纹扩展加快,当相邻两裂纹连通时,结构的承载能力急剧下降,因此也有很多失效准则研究集中于多裂纹连通准则。Swift[13]通过大量试验观测,提出了韧带屈服连通准则,该准则认为：当2个裂纹尖端塑性区发生接触时,原先的2条裂纹合并成一条长裂纹。Jeong和Brewer[14]提出了韧带平均位移准则,该准则基于韧带上平均位移的协调,指出当外载荷使韧带上假想的裂纹表面不可能闭合时,裂纹发生连通。本文采用亚临界条件,以首次裂纹连通作为多裂纹结构失效的条件,结构达到该亚临界状态时发生失效。该方法降低了分析的复杂程度,且不会造成广布疲劳损伤总寿命减少很多,工程实用性强。

最后,本文将3部分内容的分析方法有机结合,给出了一种简便易用的多部位损伤全寿命分析工程方法,通过试验研究验证了该方法的准确性和有效性。

1 裂纹萌生寿命概率分布分析模型

1.1 单细节结构裂纹萌生寿命的概率分布

一般认为,在指定应力水平S下,疲劳寿命N服从威布尔分布[5,15-16],双参威布尔分布的概率密度函数为

(1)

式中：α为形状参数,决定了概率密度函数曲线的形状；β为特征寿命,与应力水平S和α的取值有关。

载荷循环数为NR时,单细节结构裂纹萌生的概率为

(2)

1.2 多细节结构裂纹萌生寿命概率分布分析模型

广布疲劳损伤敏感结构含有大量的相似细节,这些细节的结构构型相同、应力水平相近,通常认为它们的裂纹萌生寿命服从相同的概率分布,且相互独立[17]。假设有m个完全相同的该广布疲劳损伤敏感结构件,每个结构件中的细节数为n,在第j个结构件中,各个细节的裂纹萌生寿命按大小顺序排列如下：

j∈{1,2,…,m}

式中:上标j代表第j个结构件；下标i是该结构件中各细节寿命按照从小到大顺序排列的序数。

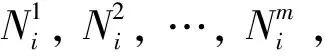
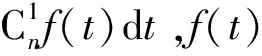
根据概率乘法定理,事件A发生的概率等于事件1～3发生概率的乘积,即

经整理,得

[1-F(t)]n-if(t)

(3)

Ni的概率分布函数为

(4)

通过式(3)和式(4),就可由单细节结构裂纹萌生寿命概率分布分别求出广布疲劳损伤敏感结构中各条裂纹萌生寿命的概率密度函数和概率分布函数。

特别地,当i=1时,Ni代表多细节结构中第1条裂纹的萌生寿命,其概率密度函数为

(5)

对比式(5)与文献[5]中串联模型的结果,两者相同。可见,串联模型是本文模型的一个特例。

2 多裂纹扩展分析的响应面法

裂纹扩展分析包含2部分工作,首先要准确计算出各裂纹尖端的应力强度因子变程,然后选择恰当的裂纹扩展速率模型,计算出裂纹扩展寿命。

2.1 多裂纹指定长度组合下的应力强度因子计算

由于多裂纹结构中含有多条裂纹,其几何边界条件比较复杂,采用解析法求解应力强度因子会遇到相当大的困难,本文采用有限元法,借助有限元软件ABAQUS进行求解。

指定多裂纹结构中各条裂纹的长度后,可按该长度建立含裂纹的有限元模型。有限元网格划分时,需在裂尖周围布置奇异元,示例见图1。经有限元计算后,可得到各条裂纹应力强度因子值。

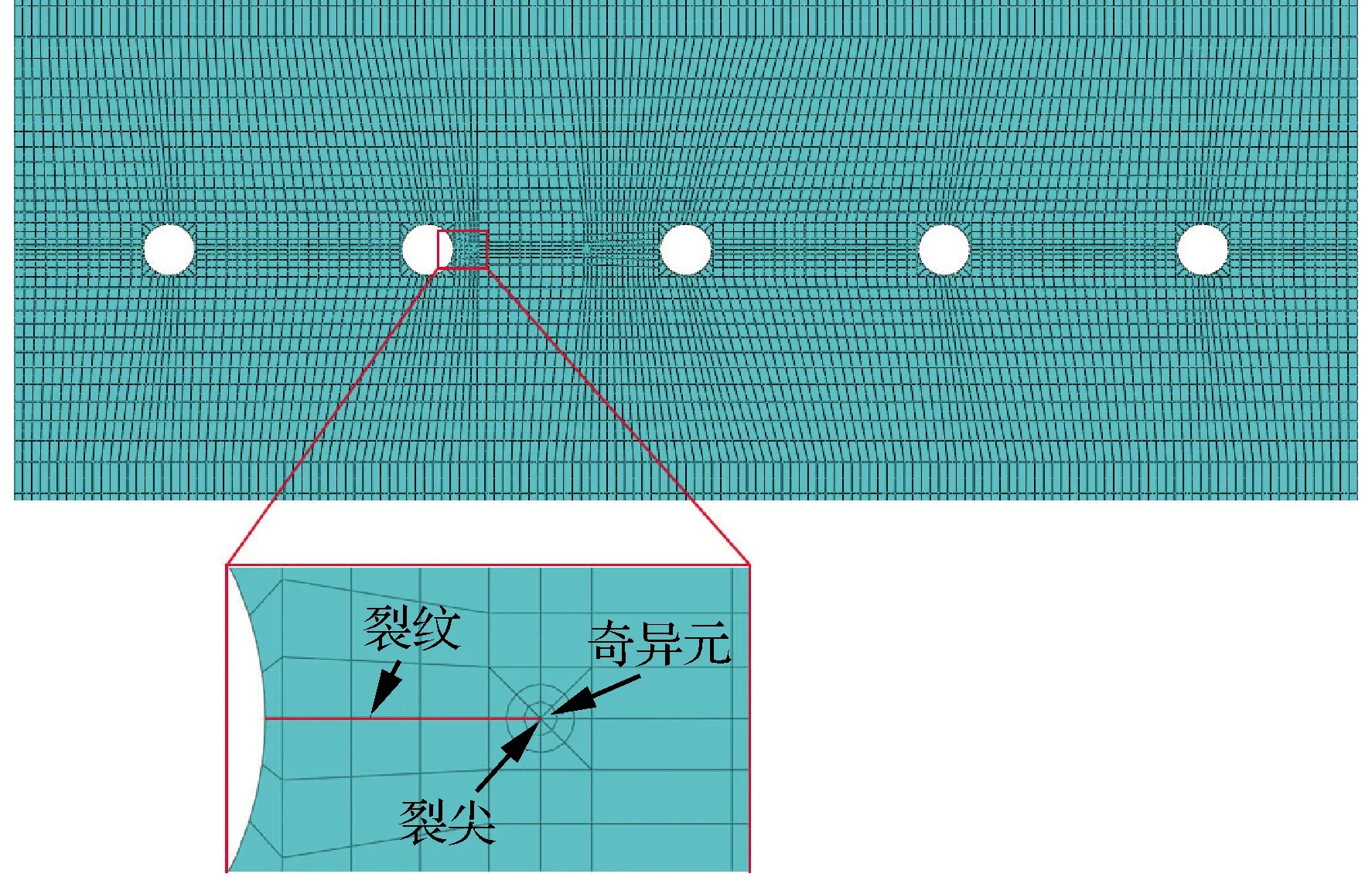
图1 含多裂纹有限元模型示意图

2.2 多裂纹任意长度组合下的应力强度因子计算

多裂纹结构含有多条裂纹,每条裂纹都有其长度,2.1节讲述了多裂纹指定长度组合下求解裂尖应力强度因子的过程。在裂纹扩展过程中,每条裂纹的长度都是不断变化的,裂纹长度组合有很多种,需要求解很多次应力强度因子。这种情况下,如果每次都通过建立有限元模型来计算应力强度因子,其计算量是巨大的,不便于实施。

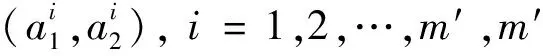
(6)

式中:

i′是面Ⅰ4个角点映射到等参坐标系后的新序号,见图2(b),原序号用括号中数字表示;Ki′是4个角点所对应裂纹长度组合下的应力强度因子值。

2.3 裂纹扩展计算

裂纹扩展分析采用循环接循环法,步骤如下：

步骤1根据1.2节的裂纹萌生寿命分析结果,在第1条裂纹萌生时,于结构上设置a0=0.5 mm 长的一条裂纹。

步骤2按2.2节的分析方法,计算裂纹长度为ai时(i=0,1,2,…,代表载荷步),各条裂纹的应力强度因子变程ΔKi：

ΔKi=Kmax(1-R)

式中：Kmax为最大应力强度因子,对应最大载荷;R为应力比。

步骤3按设置的载荷循环间隔ΔN=1计算各裂纹扩展量Δai,计算采用Paris公式[18]：

式中:C为Paris公式中材料性能系数。

步骤4计算新的裂纹长度ai+1=ai+Δai,载荷步增加ΔN=1,并返回步骤2进行循环计算。

执行步骤4后,如果裂纹长度达到结构失效临界长度,计算终止；如果到达后续裂纹萌生时间,于结构上增加一条新的初始长度为0.5 mm的裂纹,继续步骤2进行。

整个计算流程如图3所示。

3 多裂纹结构失效分析

本文采用亚临界条件来判断结构是否失效。对多部位损伤问题,认为结构上萌生的首条裂纹与第2条裂纹的位置相邻,裂纹发生首次连通时,结构失效。这样做是保守的,并且不会给全寿命带来很大程度的减少。

判断是否连通采用韧带屈服连通准则,认为当2个裂纹尖端塑性区刚好发生接触时,原先的2条裂纹合并成一条长的裂纹。假设第1条裂纹长度为a1,塑性区长度为rp1,第2条裂纹长度为a2,塑性区长度为rp2,孔半径为r,孔间距为S,各几何量示意见图4。当式(7)成立时,裂纹连通。

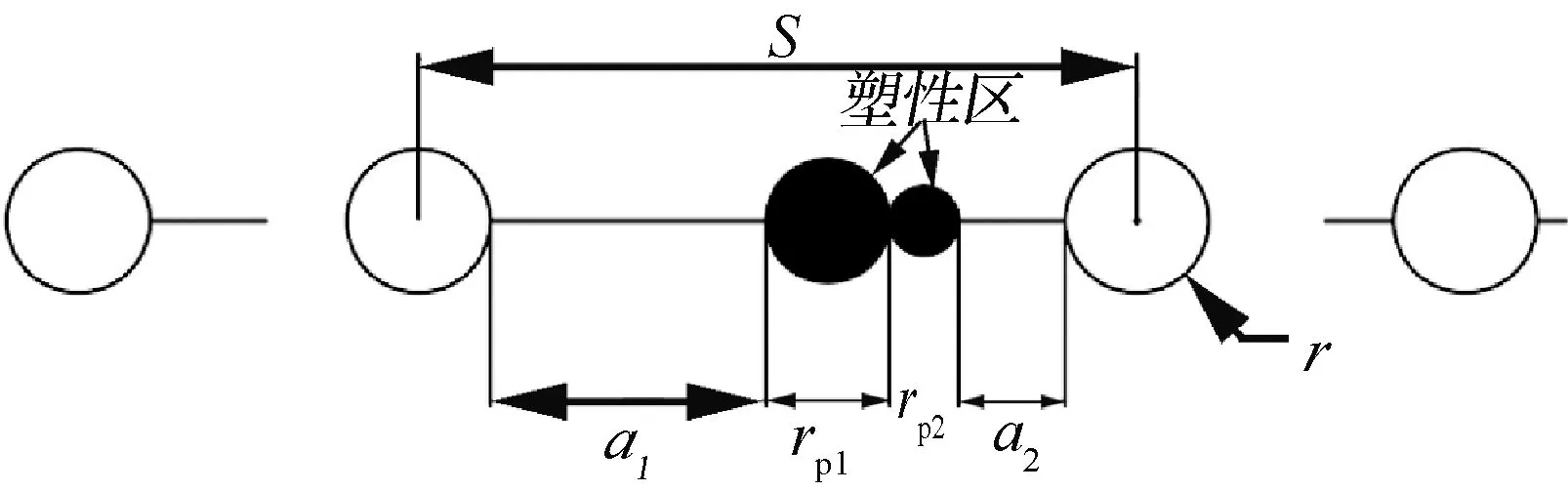
图4 韧带屈服连通示意图

a1+a2+rp1+rp2=S-2r

(7)

塑性区长度计算采用Irwin塑性区模型[19]：

(8)

式中:σys为屈服应力。

4 单细节与多细节带孔板裂纹萌生扩展试验

为了验证本文所提出分析模型的正确性,分别进行了单细节带孔板与多细节带孔板的裂纹萌生扩展试验。

4.1 单细节带孔板裂纹萌生试验

4.1.1 试验情况

试验件和试验相关情况详见文献[20],采用液压平板夹具夹持,夹持距离为30 mm,夹头间试样有效长度为120 mm,约为试样宽度5倍,能保证载荷均匀传递到试验件,可认为夹持端对孔边裂纹萌生无影响。对每个试样,根据预估寿命,每隔100 0～20 000个循环,利用观测设备观察试样是否出现裂纹。如果没有裂纹,继续进行试验；如果出现裂纹,则记录裂纹的长度和循环次数,后继观测的间隔循环数要逐渐减小,直至试样破坏。由记录数据得到试样的裂纹萌生寿命和疲劳总寿命。采用正弦波加载,最大应力水平Smax取100 MPa,应力比取R=0.06。

4.1.2 试验结果

裂纹萌生阶段,贯穿孔前后面的裂纹长度往往不等,以其中较大值达到0.5 mm时的载荷循环次数作为裂纹萌生寿命[21-22],单细节试验件在Smax=100 MPa下的裂纹萌生寿命值见表1。

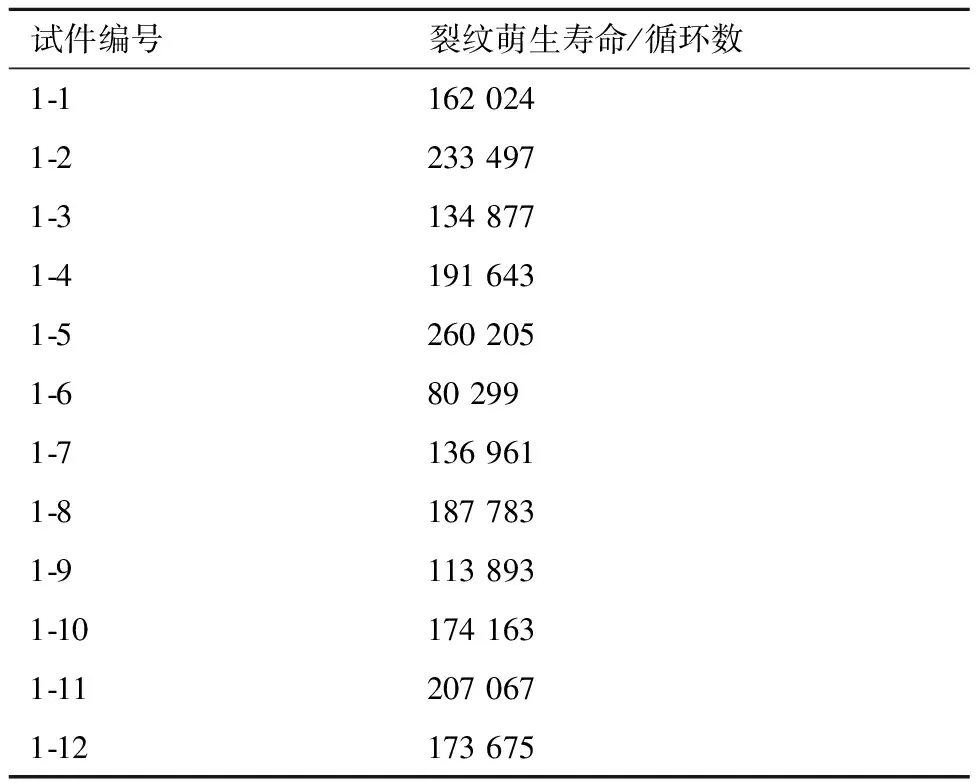
表1 单细节试件裂纹萌生寿命

4.2 多细节带孔板裂纹萌生扩展试验

4.2.1 试验情况

试验件和试验相关情况详见文献[20],采用液压平板夹具夹持,夹持距离为50 mm,3种试样夹头间有效长度分别为280、500和630 mm,由于11细节和21细节试样宽于试验机标配平板夹块,采用辅助平板夹具进行轴向加载,见文献[20]图18,能保证载荷均匀传递到试验件,可认为夹持端对孔边裂纹萌生无影响。对每个试样,根据预估寿命,每隔10 000个循环,利用观测设备观察试样是否出现裂纹：如果没有裂纹,继续进行试验；如果出现裂纹,则记录裂纹长度和载荷循环次数,后续观测的间隔循环数逐渐减小,直到裂纹扩展进入失稳扩展阶段,停止试验。由记录数据得到试样各条裂纹的萌生和扩展寿命。采用正弦波加载,最大应力水平取Smax=100 MPa,应力比取R=0.06。

4.2.2 试验结果

5细节试验件的第1、第2条裂纹萌生和首次连通寿命值见表2,11细节试验件的第1、第2、第3条裂纹萌生和首次连通寿命值见表3,21细节试验件的第1、第2、第3、第4条裂纹萌生和首次连通寿命值见表4。

表2 5细节试件裂纹萌生寿命和首次连通寿命

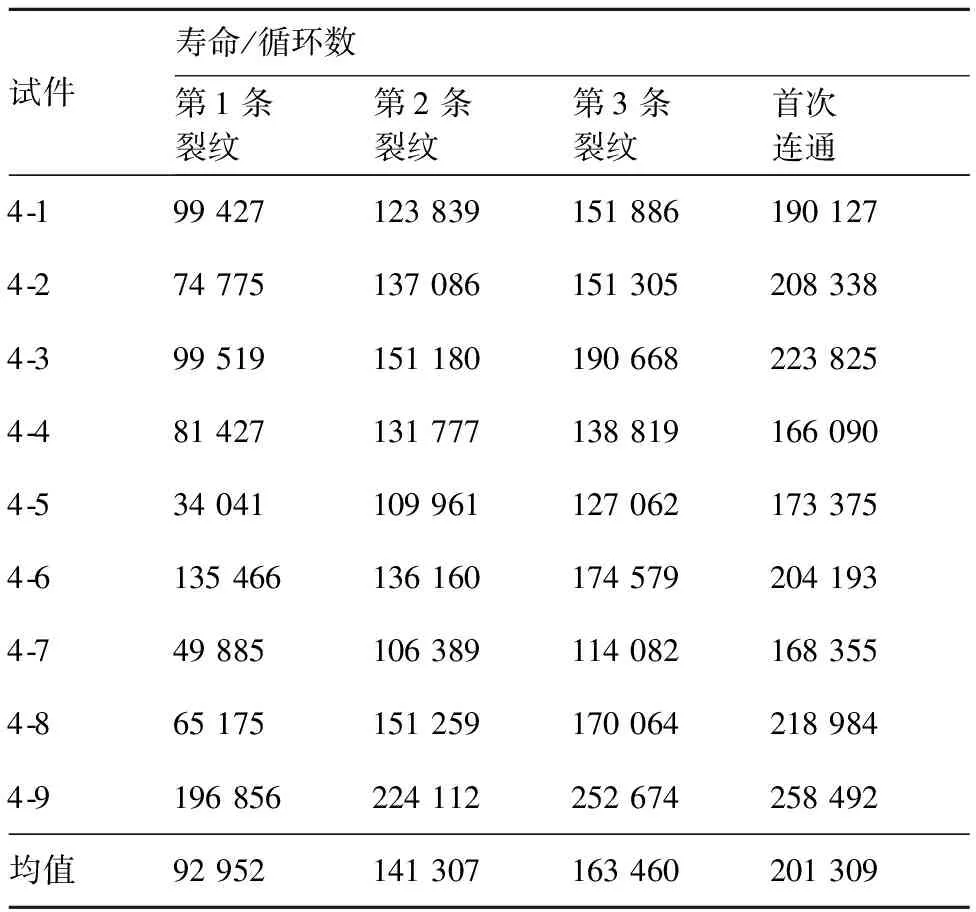
表3 11细节试件裂纹萌生寿命和首次连通寿命

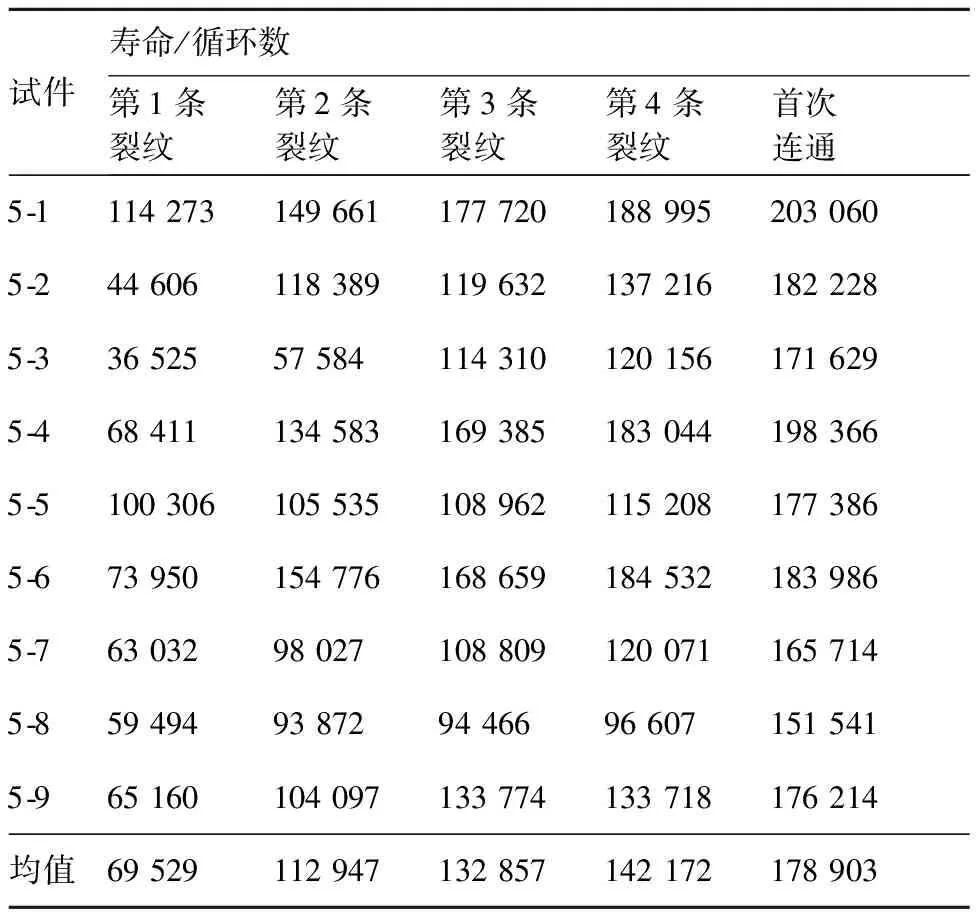
表4 21细节试件裂纹萌生寿命和首次连通寿命

5 数据分析

5.1 裂纹萌生寿命分析

对单细节带孔板裂纹萌生寿命试验结果进行统计分析,得到其概率分布,再应用本文分析模型预测多细节带孔板各条裂纹的萌生寿命,并与试验结果进行对比。

采用最大似然法[23]对裂纹萌生寿命数据进行统计处理,参数估计的极大似然估计方程为

(9)

(10)

式中：ti是各试件的寿命值。先用数值迭代解法通过式(9)解出α值,再由式(10)求出β值。

对单细节带孔板裂纹萌生寿命数据进行处理,得到α=3.99,β=189 218。所以,单细节裂纹萌生寿命的概率密度函数为

(11)

概率分布函数为

(12)

将式(11)和(12)代入式(3),预测得到第i条裂纹萌生寿命Ni的概率密度函数,继而由式(4)得到Ni的概率分布函数,再由概率分布函数得到可靠度为36.8%时的寿命。

采用同样的统计方法对多细节带孔板裂纹萌生寿命的试验值进行处理,得到α和β值,β值即是36.8%可靠度的寿命,结果见表5。

36.8%可靠度寿命的预测值Npre与试验值Nexp的对比见表5和图5。为说明本文模型与以往裂纹萌生寿命分析模型的差异,在表5中也给出了文献[5～6]的预测结果,可见,3种模型的第1条裂纹萌生寿命预测值几乎一致,但文献[6]中的模型无法预测后续裂纹(第2条及以后)的萌生寿命,文献[5]中的模型对后续裂纹萌生寿命的预测过于保守。

从表5可见,本文模型预测值与试验值很接近,由图5也可以看出,预测寿命均落在试验寿命2倍分散带范围内,除21细节第1条裂纹萌生寿命预测值略大于试验值以外,其他预测值均偏保守,预测效果良好。

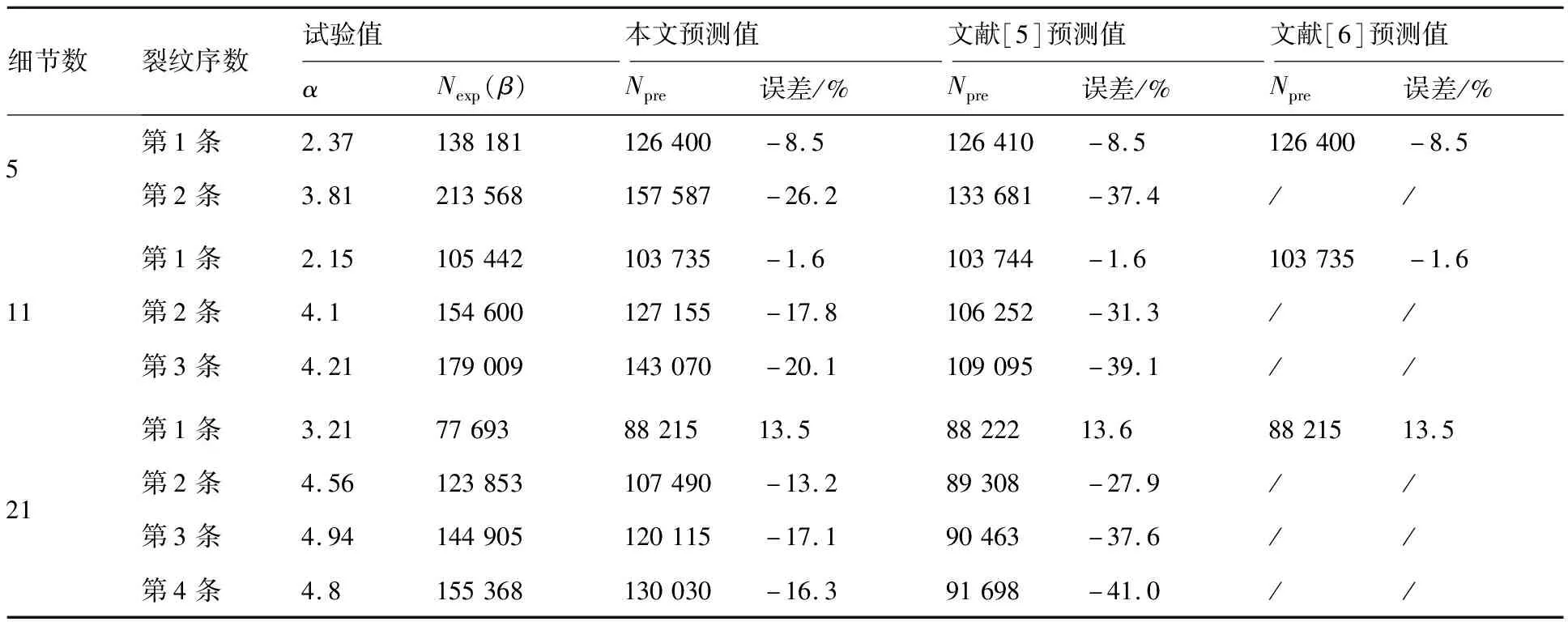
表5 裂纹萌生寿命预测值与试验值

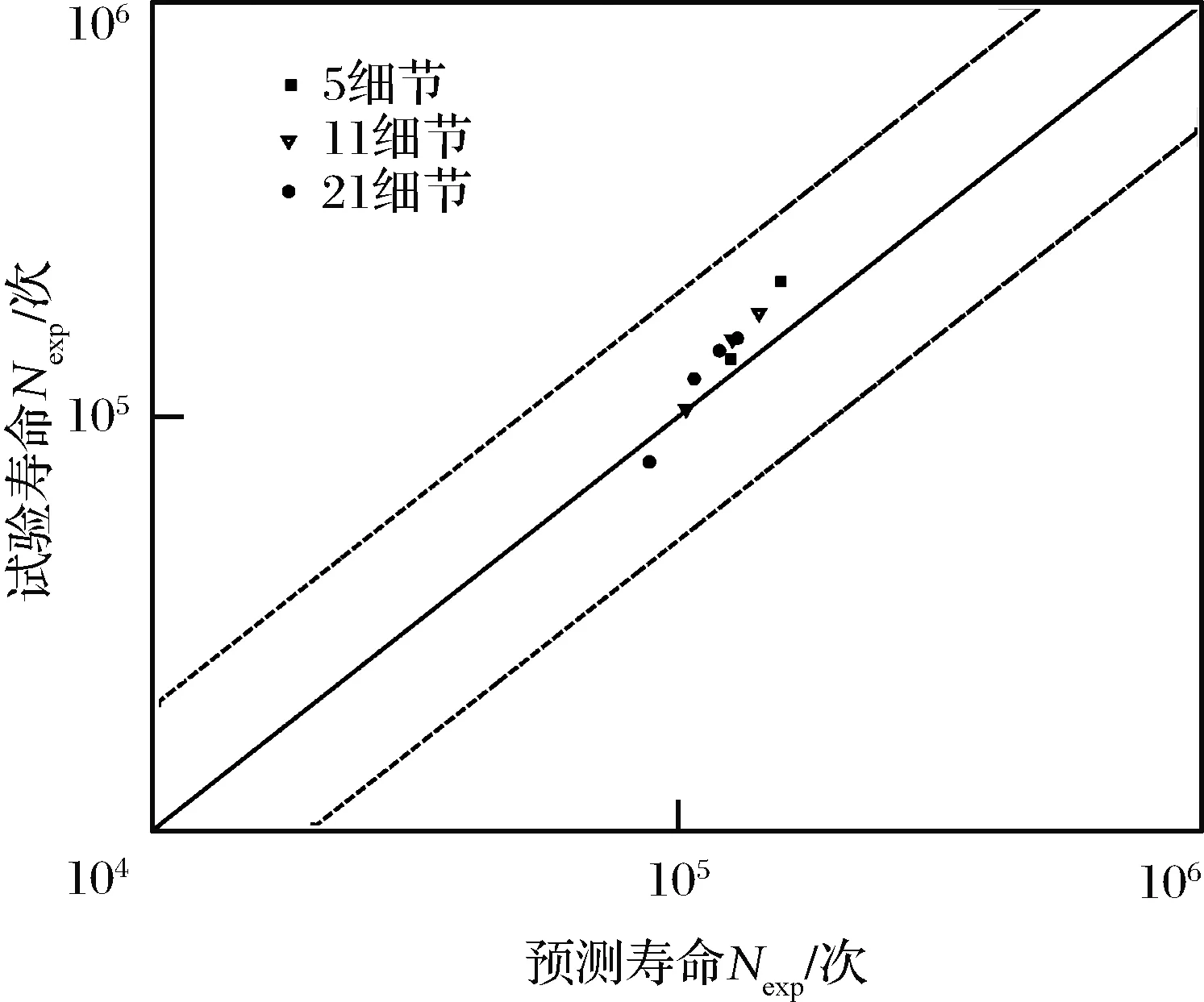
图5 裂纹萌生寿命预测值与试验值对比

5.2 裂纹扩展寿命分析

5.2.1 5细节孔板应力强度因子响应面构造

由于保守假定结构上萌生的头两条裂纹位置相邻,且采用首次裂纹连通作为结构失效准则,因此,只需考虑同时存在两条裂纹的情况。

为构造响应面,先采用均匀设计法进行试验设计,确定若干裂纹长度组合作为样本点。再建立这些样本裂纹长度组合下的有限元模型,为使建模过程自动化,本文采用Python语言编写参数化建模程序。建模完成后,按2.1节方法计算两条裂纹尖端的应力强度因子值。

5细节孔板2条裂纹在试验设计样本点下的应力强度因子计算值分别见表6和表7,K1代表第1条裂纹的应力强度因子,a1代表第1条裂纹的长度,K2代表第2条裂纹的应力强度因子,a2代表第2条裂纹的长度。

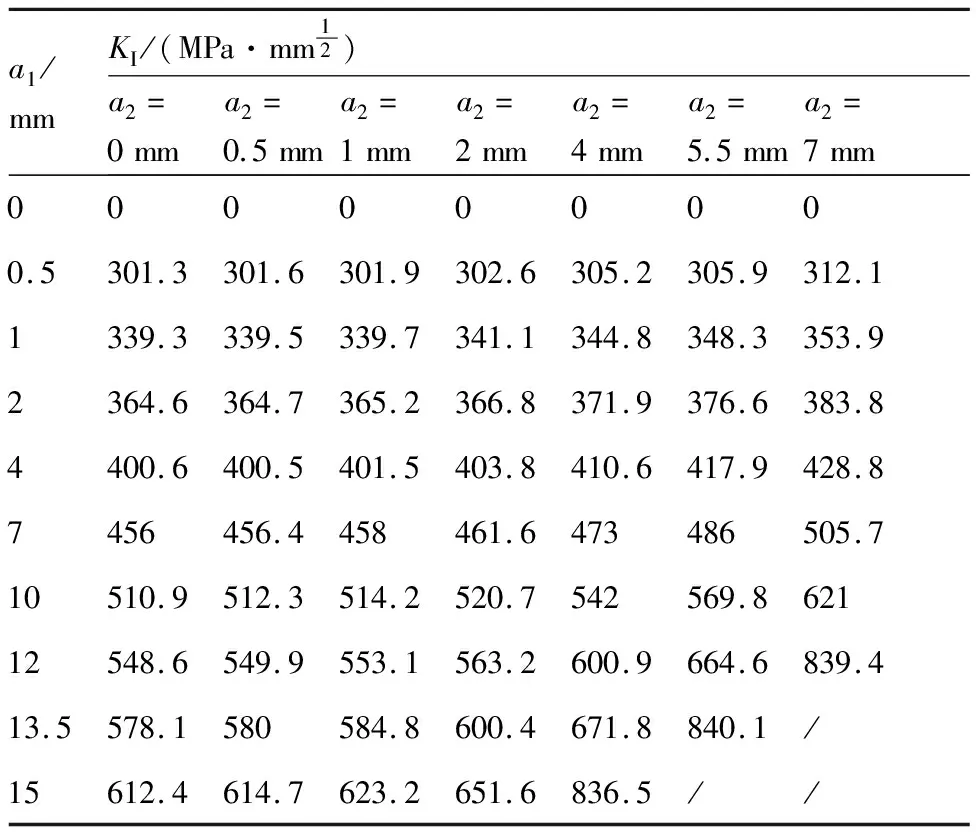
表6 5细节孔板2条裂纹长度组合样本下第1条裂纹的应力强度因子值K1

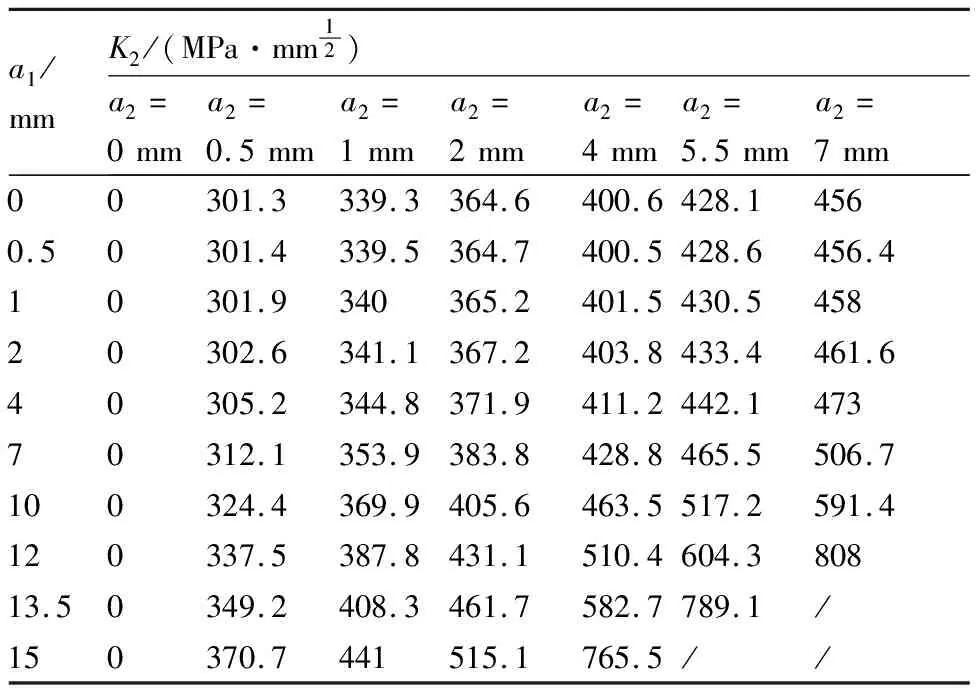
表7 5细节孔板2条裂纹长度组合样本下第2条裂纹的应力强度因子值K2

用线性模型对这些样本点进行近似拟合,建立两条裂纹裂尖应力强度因子的响应面,分别见图6和图7。

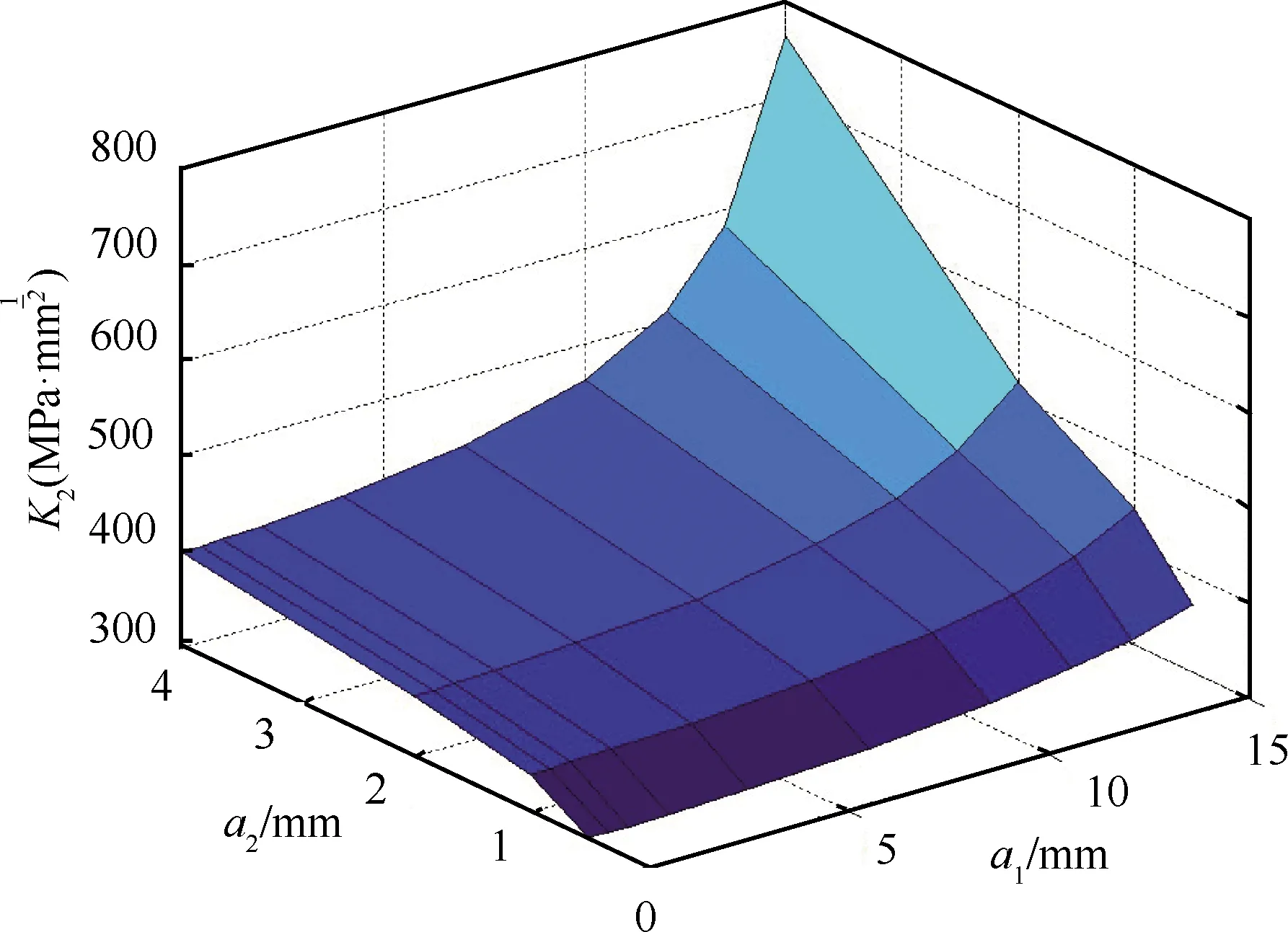
图7 5细节孔板第2条裂纹裂尖应力强度因子K2响应面

为表明响应面法计算多裂纹应力强度因子的可行性,利用上文所建响应面计算了一系列裂纹长度组合下的裂尖应力强度因子值,并与ABAQUS计算结果进行了对比,见表8,可见响应面法计算误差很小,且计算花费时间大幅缩短。

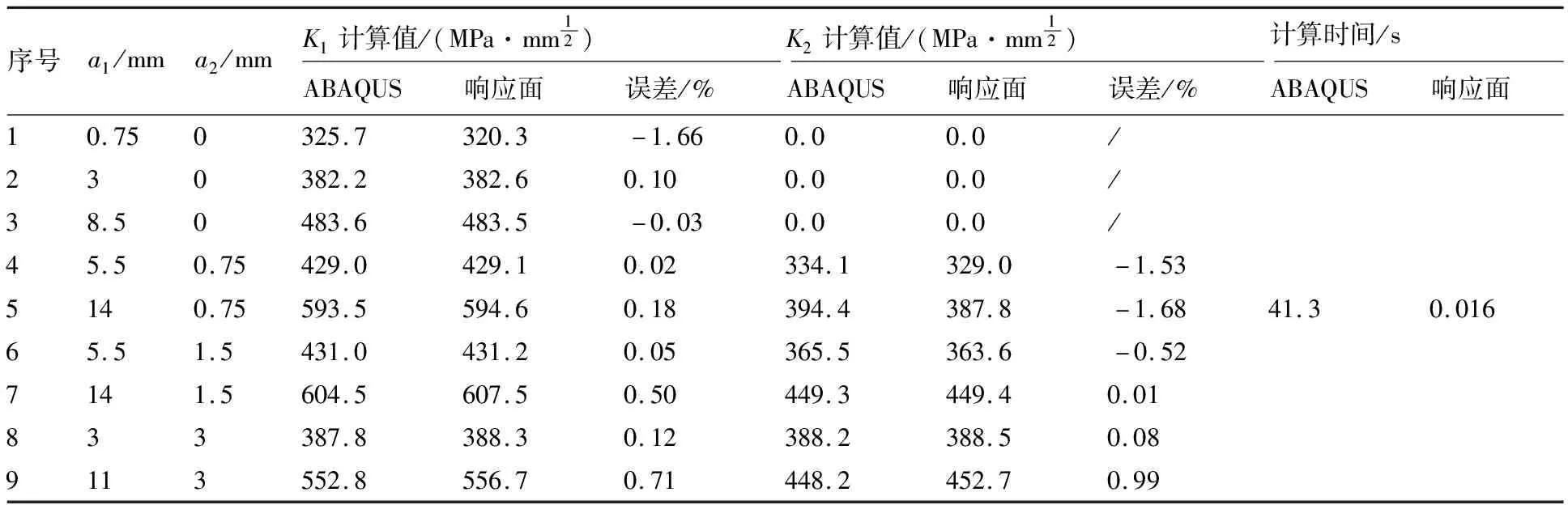
表8 响应面法与常规有限元法多裂纹应力强度因子计算结果和计算效率对比

5.2.2 5细节孔板裂纹扩展计算

按2.3节的循环接循环方式计算裂纹扩展。以5细节试件3-1为例,循环载荷施加到121 241 次时,在第2个孔(从左向右数)的左侧萌生第1条裂纹,此时将第1条裂纹长度设置成0.5 mm,开始裂纹扩展计算。首先应用响应面模型,计算应力强度因子变程。再计算1个载荷循环下的裂纹扩展量,计算时材料常数取自试验数据,C=6.74×10-8,n=2.85,按裂纹扩展量更新裂纹长度。循环计算,直至190 389次循环时,在第1个孔的右侧萌生第2条裂纹(注：结构中实际第2条裂纹萌生在第4个孔的左侧,由于与第1条裂纹的位置不相邻,在不影响裂纹扩展分析模型验证的情况下,这里选择后续萌生的位置相邻裂纹作为第2条裂纹进行计算),此时将第2条裂纹长度设置为0.5 mm。再继续进行循环计算。当2条裂纹的塑性区发生连通时,计算终止。裂纹扩展试验数据见表9,裂纹扩展预测曲线与试验数据的对比见图8。

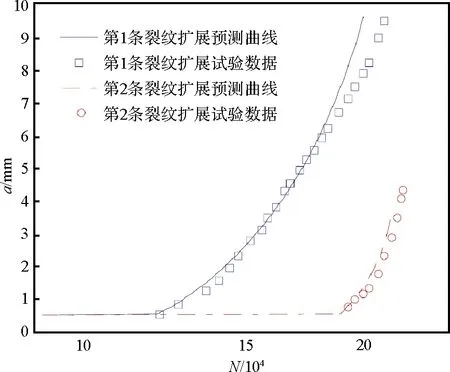
图8 试件裂纹扩展预测曲线与试验数据对比

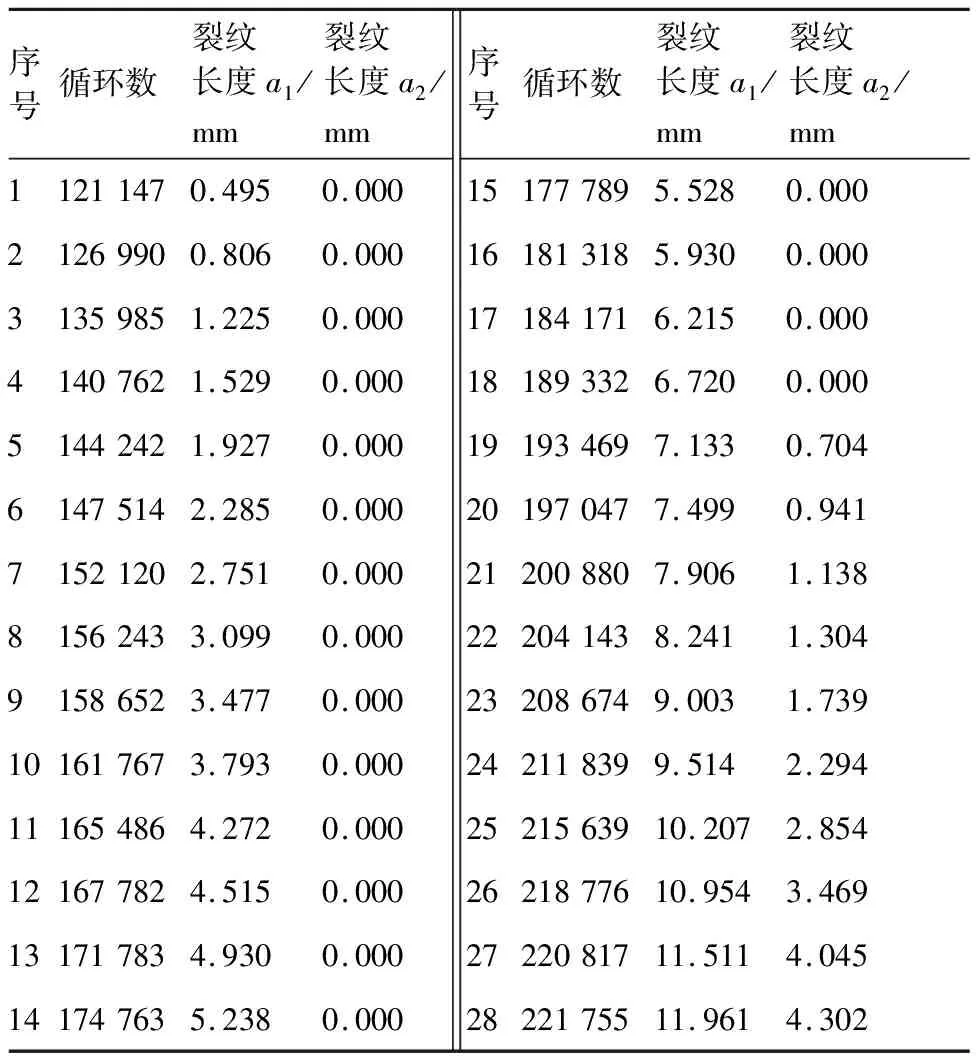
表9 试件3-1裂纹扩展试验数据

11细节和21细节试件的裂纹扩展预测曲线和试验数据也符合较好,具体计算过程在此不再赘述。说明本文提出的裂纹扩展寿命分析方法满足工程计算准确度要求。

5.3 全寿命分析

带孔板裂纹萌生扩展问题是多部位损伤问题,进行失效分析时,保守认为结构上萌生的首条裂纹与第2条裂纹的位置相邻,当它们发生首次连通时,结构失效。

根据5.1节裂纹萌生寿命预测结果,见表5,在第1条裂纹萌生预测时间点(36.8%可靠度寿命),于裂纹扩展计算模型中设置第1条裂纹。按2.3节的循环接循环方式计算第1条裂纹的扩展。在第2条裂纹萌生预测时间点(36.8%可靠度寿命),设置第2条裂纹。同时进行2条裂纹扩展的计算。当裂纹连通时,终止计算。分别得到了5细节、11细节和21细节孔板裂纹首次连通时间的预测值,也是36.8%可靠度寿命,它们与试验值的对比见表10。可见预测值均非常接近试验值,且偏小,是保守的。证明本文的多部位损伤全寿命分析模型的预测效果令人满意。