影响航空发动机结构寿命的载荷分散系数
2021-06-16杨俊杰郑小梅杨兴宇
杨俊杰,郑小梅,杨兴宇,*
1.清华大学 航空发动机研究院,北京 100084
2.北京航空工程研究中心,北京 100076
航空发动机疲劳分散系数是寿命评定中的一个重要可靠性指标,与飞行安全性关系极大。疲劳分散系数的研究起源于飞机结构疲劳寿命的确定,但是各国在规范的制定上并不统一且取值混乱[1],一定程度上表明航空发动机疲劳分散系数的确定仍然有待进一步深入研究。
中国在飞机结构疲劳分散系数方面进行了大量的研究,早在GJB67.6-85中就对疲劳分散系数做了详细解释:“由于疲劳试验固有的分散性及飞机服役中所经受的使用载荷谱有可能比设计使用载荷谱更严重等原因,在确定飞机结构使用寿命时,应考虑疲劳分散系数。[2]”并在其最新版本的规范GJB67.6A-2008中,将疲劳分散系数描述为“是用于描述疲劳分析和试验结果的寿命可靠性系数,它是由寿命的分布函数、标准差、可靠性要求和服役经验得出的。[3]”但是,飞机结构疲劳分散系数的明确数学定义却是高镇同在其著作中较早提出的,即为中值寿命与一定置信度、可靠度的寿命的比值[4]。
张福泽[5]将疲劳分散系数分成疲劳试验用的分散系数和理论计算用的分散系数,其中每一种又可以分为裂纹形成寿命的分散系数和裂纹扩展寿命的分散系数。这种方法成为Yan和Lin[6]建立中国飞机经济寿命模型的基础,即通过飞机结构的全面测试结果以及裂纹萌生阶段和裂纹扩展阶段的疲劳分散系数,确定飞机的经济寿命和检查周期。目前,飞机的经济寿命预测和飞机结构可靠性评估的理论已成功应用于确定和延长数千架飞机的结构寿命,并且可以确保飞机结构的安全性和可靠性。
刘文珽和贺小凡等[7-9]对单机结构疲劳分散系数[7]和机群定寿的载荷分散系数进行了深入阐述,将疲劳分散系数分为两部分:单机结构分散系数和载荷分散系数。并对载荷分散系数进行了研究,编制了某型飞机11种反映机群不同使用强度的单机载荷谱,开展了单机载荷谱下典型结构模拟件成组疲劳试验,确定出可靠度90%的载荷分散系数在1.56~1.60之间[7]。
相对于飞机,国内在航空发动机结构疲劳分散性方面的研究滞后多年,并没有形成系统的研究成果。国内在引进《斯贝MK202发动机应力标准》(EGD-3)和Def Stan 00-971《燃气涡轮发动机通用规范》[10]后,部分学者在该领域开展了探讨和研究。陆山等[11]推导出服从对数正态分布的基于小子样最好和最差试验结果的寿命分散系数法;卢小艳和陆山[12]研究了服从对数正态分布和韦布尔分布的、基于任意第K试验疲劳寿命分散系数的计算公式;王卫国[13]开展的轮盘小子样试验寿命可靠性评估方法研究,给出了服从对数正态分布和双参数韦布尔分布的小子样疲劳寿命分散系数;杨俊等[14]就疲劳分散系数在轮盘低周疲劳寿命的工程计算方面做了一定的研究。上述研究集中在结构的抗疲劳特性随机化上,如果把结构疲劳的原因分为内因和外因的话,结构的抗疲劳归于内因,而疲劳载荷则属于外因。也就是说,在结构的疲劳因素随机化研究和工程应用上,载荷随机化方面研究很少。
经过多年的实践,可以看到《斯贝MK202 发动机应力标准》(EGD-3)和Def Stan 00-971关于结构疲劳分散性是一脉相承的,非常规范和统一,但仅仅限于材料结构方面的分散性,并没有考虑使用中载荷的差异性。而美国关于航空发动机通用规范和指南没有明确的规定和方法,只是在规定循环寿命时给出了2倍或1~2倍的低周疲劳寿命储备,但是也没有明确是材料结构和制造方面的还是使用载荷方面的差异。
本文在前期相关研究的基础上,对航空发动机的疲劳分散系数进行了工程定义,并将其分成两类因素:结构分散系数和载荷分散系数,其中对载荷分散系数开展了定量研究,其结果可以较好地解释美国相关规范,并与飞机结构的载荷分散系数相一致。该研究成果将对航空发动机零部件的低周疲劳可靠性工程设计方法能起到促进作用。
1 结构疲劳分散系数的规定和确定方法
1.1 英国的通用规范
1967年,英国发布军标《航空燃气涡轮发动机试验要求通用规范D Eng RD 2100》和《航空燃气涡轮发动机和喷管设计与制造通用规范D Eng RD 2300》,为燃气涡轮发动机的发展提供了需求和指导。1967—2006年,英国国防部只发布了2部航空发动机规范,即1987年5月29日发布的用以代替之前D Eng RD 2100 和2300的Def Stan 00-971《燃气涡轮发动机通用规范》,和2006年1月27日发布的用以替代前者的Def Stan 00-970-11《飞机用设计和适航性要求,11部—发动机》[15]。自此,Def Stan 00-970-11成为最新的英国军用航空涡轮发动机通用规范。
在航空发动机零部件的低周疲劳可靠性工程设计和寿命评估中,最成功并沿用至今的是英国R&R公司的《斯贝MK202发动机应力标准》(EGD-3)使用的名义应力方法。包括该标准在内的许多设计和试验资料,都体现了Def Stan 00-971 的要求,也为正确理解Def Stan 00-971提供了极好的例证。
EGD-3中的名义应力方法以大量的零部件试验为基础,给出了常用的不同类别材料的疲劳强度分散系数、不同应力集中系数的S-N曲线,零部件的寿命分散度以“最好”和“最坏”S-N曲线的方式表示出来。EGD-3详细规定了疲劳强度分散系数的确定方法,例如对于一般结构件,假设材料强度极限的分散系数与循环寿命无关,而疲劳强度分散系数与循环寿命相关:大于105和小于104无关,在104~105之间与对数循环寿命线性相关。疲劳强度分散系数同时考虑了材料类型和加工工艺的差异:锻件或机械加工件归结为一类;铸件或焊接件归结为一类。上述两类结构件(或不同加工工艺)有着相似的规律,但是取值存在差异。应力集中系数主要考虑了结构件的焊缝、孔和缺口等几何形状的不连续性对疲劳寿命的影响。EGD-3假设应力集中系数值在小于103循环时为1.0,大于106循环时为常数,在103~106之间与对数寿命呈线性变化。
Def Stan 00-971标准对EGD-3的方法进行了改进,推荐了不同试验子样情况下的寿命散度。Def Stan 00-971规定,疲劳寿命分布可以是韦布尔分布,也可以是对数正态分布。并按对数正态分布以表格的形式给出了各种试验件数量对应的寿命分散系数。当试验的零件多于一个时,这种方法允许对试验结果的平均值或最低值使用减小的分散系数,或者对最好的试验结果用单件试验的分散系数。只要试验结果没有显示分散系数大于在基本分布中的假定值,就可以使用安全寿命的最高估计值。
Def Stan 00-970-11明确了寿命分散系数y定义,是指用于将试验所得的关键部位的等效发动机循环数与安全循环寿命相联系的材料分散系数。并明确了,y是N+95%与N-3σ比值的估计值。该规范还给出了采用应力分散系数α和寿命分散系数y,根据疲劳试验循环数N确定试验批准的安全寿命Fr的计算公式:
(1)
与Def Stan 00-971相比,Def Stan 00-970-11在关键件定寿方法、安全寿命的试验分散系数推导和裂纹扩展评定、锻件的安全寿命评定(裂纹萌生)、子样分散性评定、分散系数评定、裂纹扩展寿命等方面规定的更为详细、规范,特别指明裂纹萌生的安全寿命评定是适用于钢、钛合金和镍基合金等锻件结构件。2个军标最大的区别是新标准考虑损伤容限即裂纹扩展寿命阶段,且使用任务换算率监控低周疲劳寿命,并且换算率也被分成两类,即裂纹萌生的换算率和裂纹扩展的换算率。
可以看出,英军标关于关键件低周疲劳可靠性工程设计方法基本思想一脉相承,仅考虑了反映材料和加工工艺造成的零部件的寿命分散度,而没有考虑使用载荷分散度。
1.2 美国的通用规范
1973—1988年,美国共发布了MIL-E-5007D、MIL-E-5007E和MIL-E-5007F 3个版本的《航空涡轮喷气和涡轮风扇发动机通用规范》海军标准。1984年,美国空军发布了MIL-STD-1783《发动机结构完整性大纲》(Engine Structural Integrity Program,ENSIP)[16],该文件被1985年美国空军发布的MIL-E-87231《涡喷、涡扇发动机军用规范》的结构完整性部分所采用。直到1999年和2002年,MIL-STD-1783才依次被其修订版MIL-HDBK-1783A和MIL-HDBK-1783B所代替。
JSGS-87231A《航空涡轮发动机使用指导规范》[17]于1995年发布,用以代替MIL-E-87231。作为JSGS-87231A使用指导规范的修订版, JSSG-2007《航空涡喷涡扇涡轴涡桨发动机联合使用规范指南》于1998年发布,但是该指南并不是规范,并在2007年被JSSG-2007B指南替代。
由此可见,美国军用航空发动机通用规范最多[18]。但除了MIL-E-5007D之外,均明确要求低周疲劳寿命取B0.1寿命,即假设寿命分布是韦布尔分布,破坏率为0.1%的寿命。且只对关键件的疲劳寿命提出了要求,而没有提供任何具体的工程定寿方法和分散系数。
在JSGS-87231A中有一个确定高压涡轮盘低周疲劳试验循环数的例子,假设涡轮盘疲劳寿命破坏分布满足形状参数为3的双参数韦布尔概率分布,由此例可以看出,为批准高压涡轮盘4 000 循环安全寿命,必须试验3个零件,都达到36 630循环,且无一破坏,可以满足置信度为90%的要求。即试验3件,要求的寿命分散系数大于9。但是在该规范执行3年后发布的该规范执行指南JSSG-2007中,又将该例子删除了,并将要求试验3件改成试验2件。没有再提供任何其他的定寿方法。
通过对美国以上规范或指南的解读可以看出,其关于结构完整性和低周疲劳寿命方面共同要求有以下内容:
1)均有冷件、热件的区分。
2)有明确的低周疲劳寿命和高周疲劳寿命的要求。
3)根据发动机配装的飞机种类有明确的设计工作(任务)循环,同时也区分了冷件和热件的不同,或者有考虑寿命的飞行任务和飞行任务混频。
4)更为详细的油门杆循环。
5)MIL-E-5007D、MIL-E-5007E、MIL-E-5007F、MIL-STD-1783、MIL-HDBK-1783A、MIL-HDBK-1783B结构件的寿命储备按照设计工作循环2倍进行设计。
6)MIL-E-87231、JSGS-87231A、JSSG-2007规定结构件最低低周疲劳寿命应为设计寿命的1~2倍。
7)JSSG-2007B规定关键热件、关键冷件低周疲劳寿命至少是翻修间隔寿命的2倍。
8)配装发动机历程记录仪(或寿命计数器)监控低周疲劳寿命,除非配备有机载发动机状态监视系统。
其中MIL-STD-1783明确提出“在早期研制中,由于构件的用法、环境条件和加工质量的不确定性,需要有寿命设计储备”。通过对该军标的深入理解,明确了美军标中考虑了使用载荷的分散性,并结合具体的设计工作循环表达,其分散系数为2倍。正是因为考虑了影响寿命可靠性的使用载荷分散性,才理解了JSGS-87231A的确定高压涡轮盘试验循环数疲劳分散系数达到9的原因。
1.3 俄罗斯的有关规定
俄罗斯对航空发动机主要零件定寿用的寿命分散系数见表1。该分散系数不仅用于关键件,也用于其他零件和整机,所以相对较小。

表1 俄罗斯使用的寿命分散系数
1.4 小 结
综上所述,英国的疲劳分散系数比俄罗斯的大,比美国的小,且有长期的使用经验。而且既有应力分散系数,又有寿命分散系数,比较完整,使用方便。Def Stan00-970-11增加要求用试验结果对该假定进行检验,以考虑对非传统材料(如粉末冶金材料)的适用性。特别重要的是,这些分散系数的使用时间已经超过半个世纪,在结合外场严密监控疲劳寿命消耗的前提下,证明安全性可以满足适航性标准的要求。
2 发动机机群定寿时的疲劳分散系数
发动机机群定寿的疲劳分散系数取决于使用寿命指定的可靠性要求,它主要包含2个方面:一是由于结构材料和制造质量分散性对应的可靠度;二是使用载荷分散性对应的可靠度。因此对应的结构疲劳分散系数也分成2个部分:结构分散系数和载荷分散系数。结构分散系数是指由于材料性能差异、结构尺寸差异、加工工艺差异等结构本身固有的分散性,而使用的寿命可靠性系数。载荷分散系数是指由于发动机在服役过程中,由于所经受载荷严重程度有差异,而使用的寿命可靠性系数。
机群定寿时所使用的疲劳分散系数应为结构分散系数和载荷分散系数的乘积,即
Lf=Lfl×Lfd
(2)
式中:Lfl为载荷分散系数,各种军标没有规定航空发动机结构件对应的可靠度,可采用90%的可靠度;Lfd为结构分散系数,对应关键件安全寿命的要求为99.87%的可靠度和95%的置信度。
在服役使用中如果进行单台发动机载荷(寿命)监控的,若监控载荷、应力和寿命模型非常准确,则在疲劳寿命评估中仅考虑结构分散系数即可;若监控载荷、应力和寿命模型不是非常准确时,则要考虑载荷差异引起的载荷分散系数。
假设航空发动机疲劳载荷的统计分布规律符合韦布尔概率密度函数:
X0≤x<∞
(3)
式中:X0为最小寿命参数;Xa为特征寿命参数;b为韦布尔形状参数。
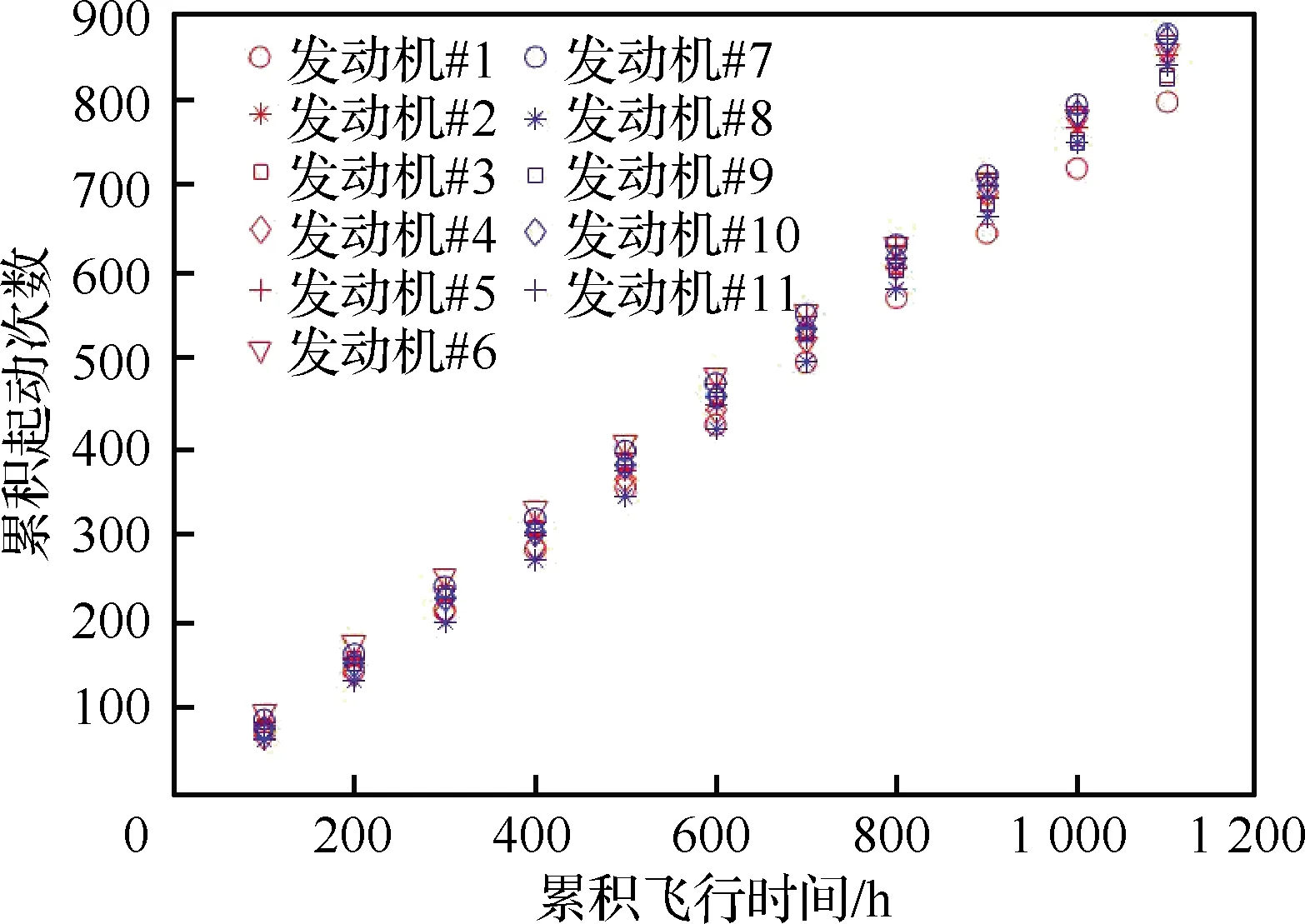
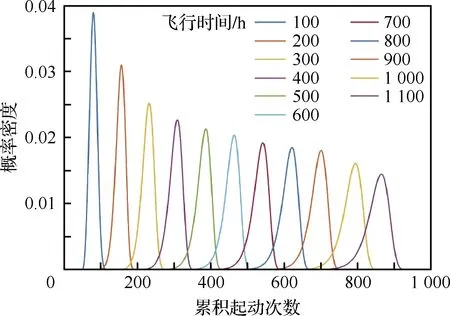
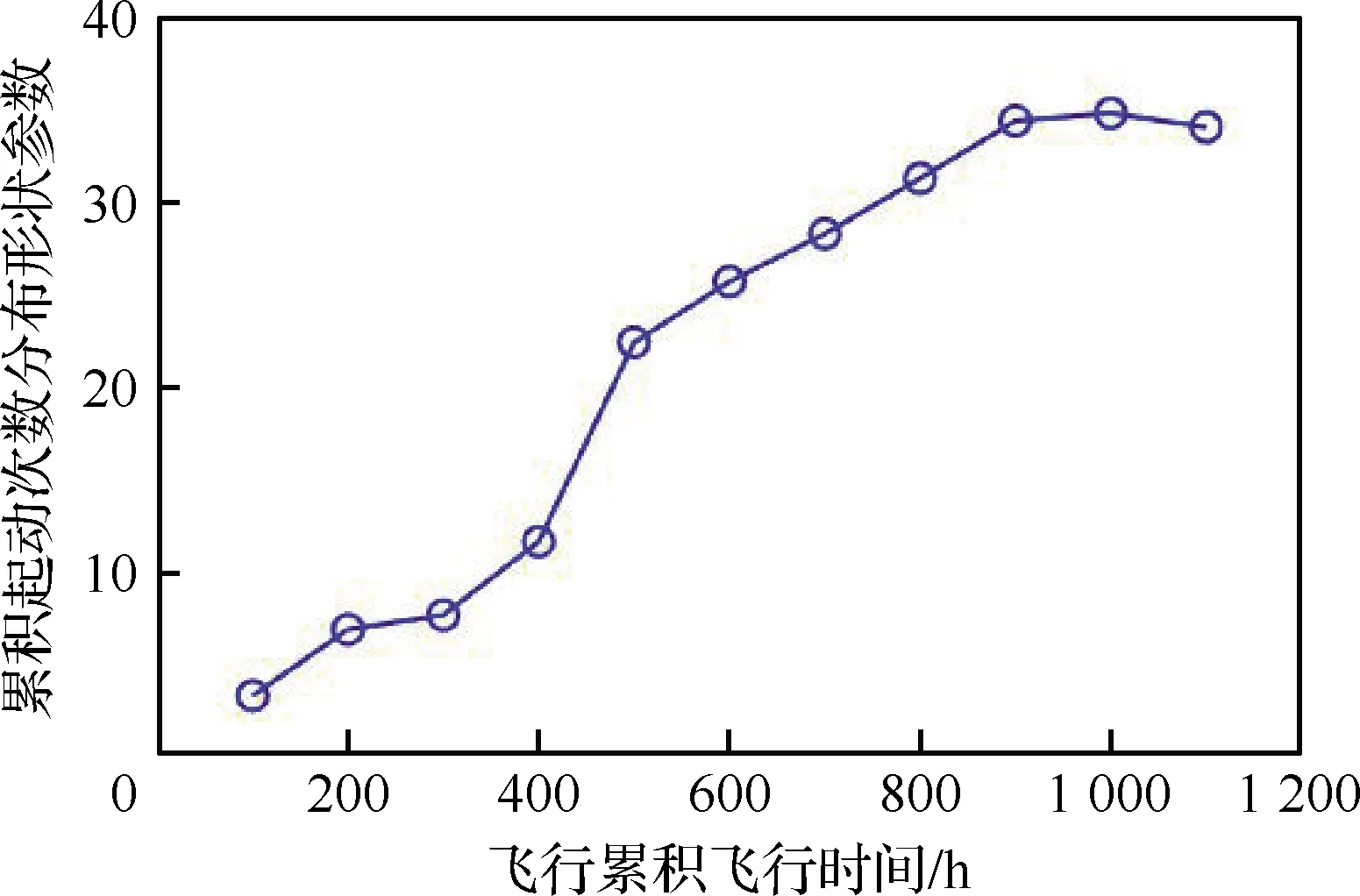
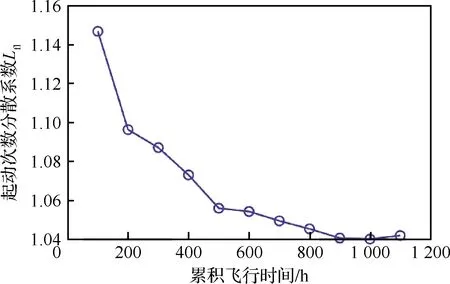
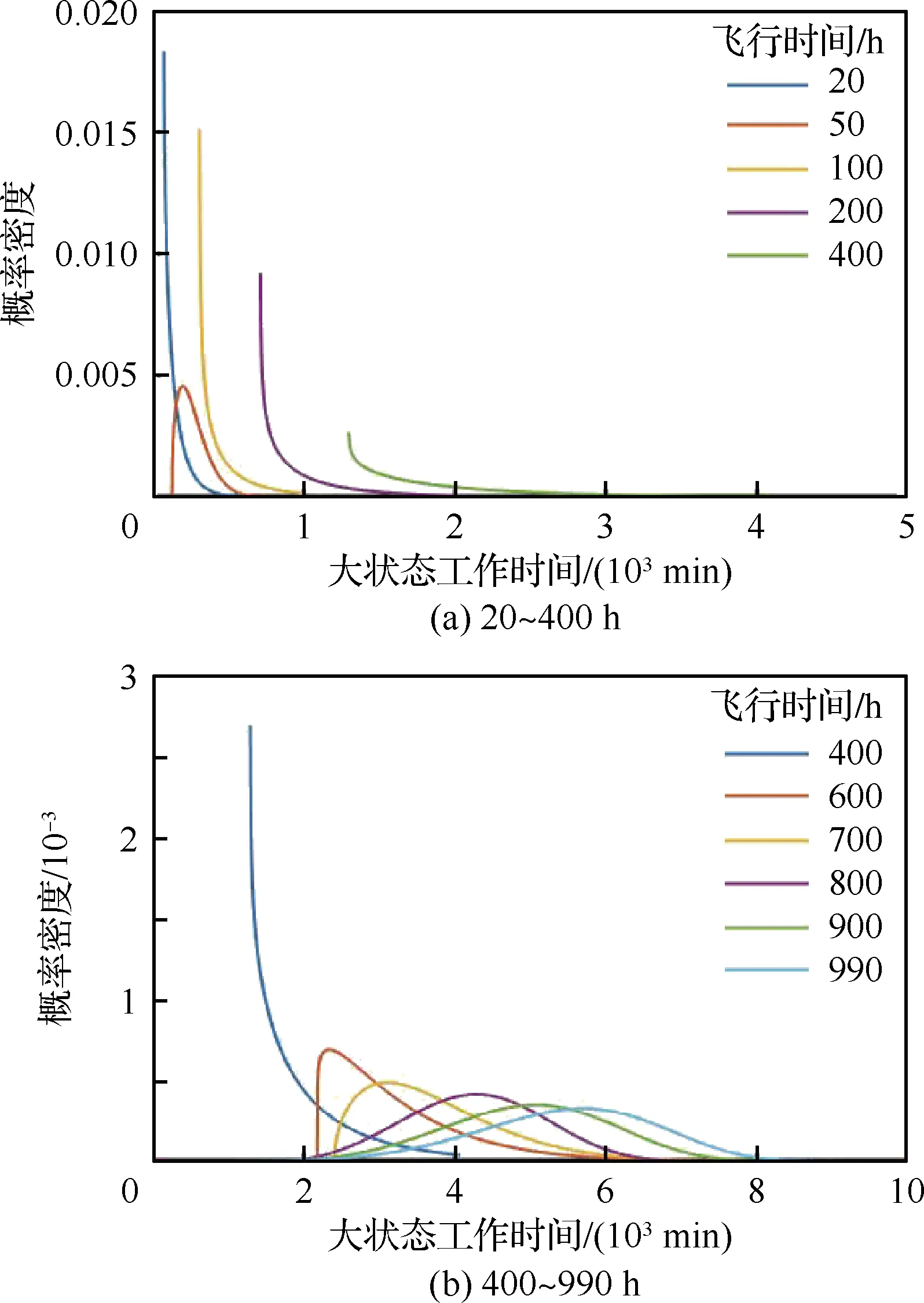
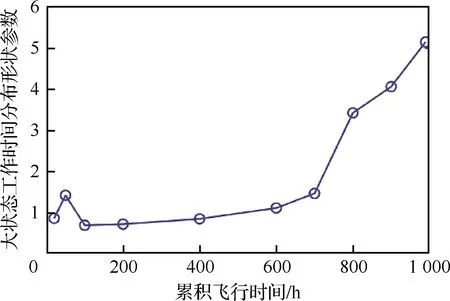
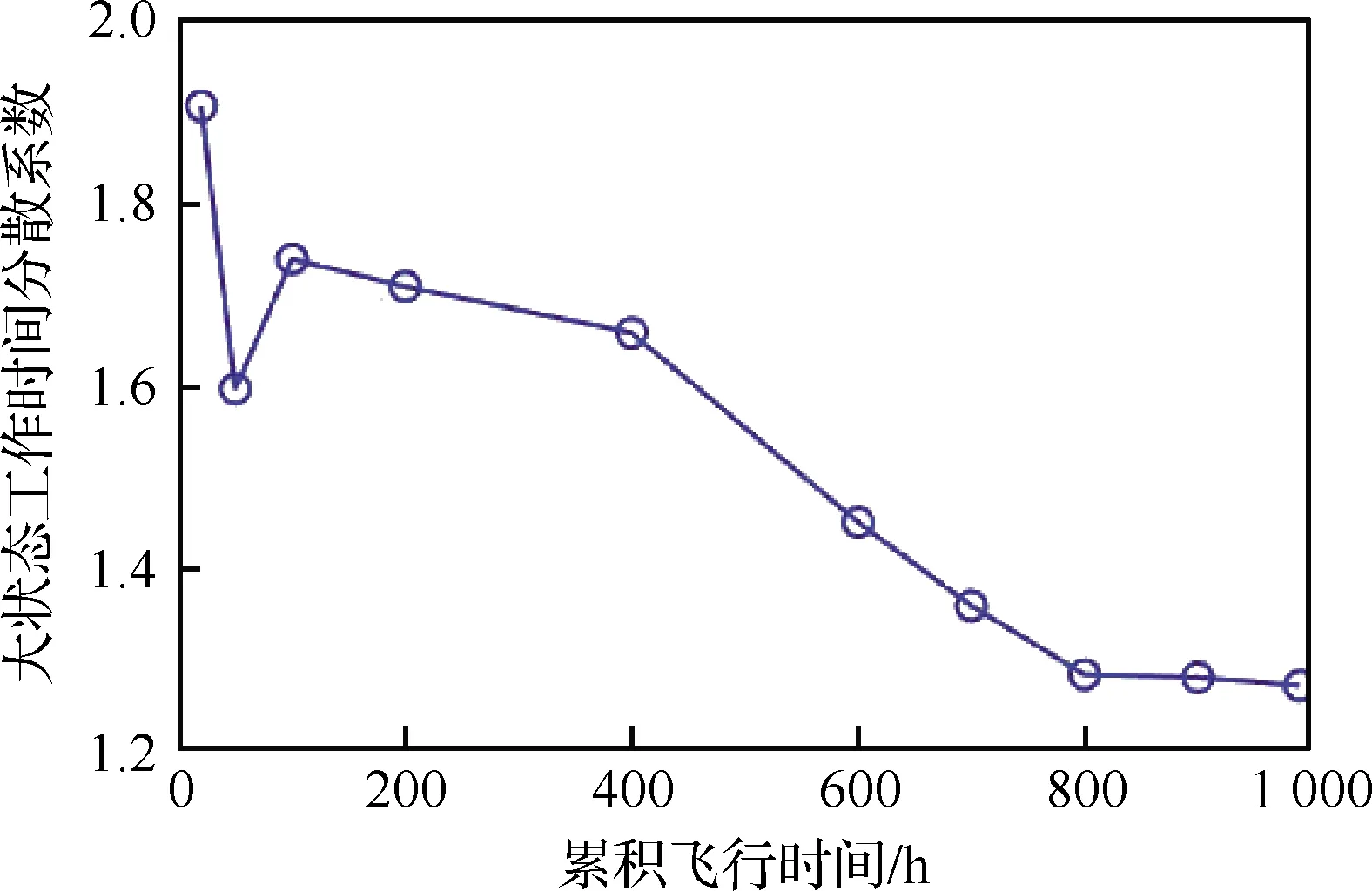
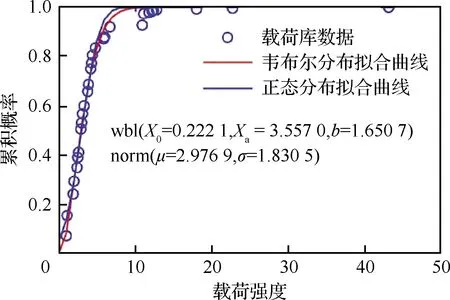
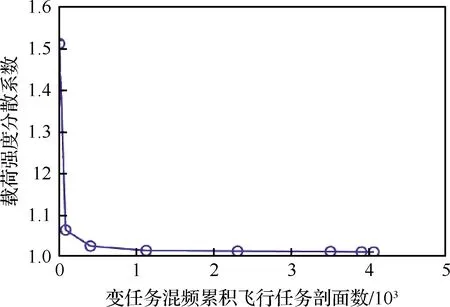
可以确定韦布尔变量的分布函数F(Xp),即介于最小参数X0和某数值Xp(p为可靠度)之间的概率P(X0 (4) 按照Miner线性损伤理论,将载荷分散系数Lfl定义为 (5) 式中:F90、F50分别为发动机统计母体使用载荷分布累积概率在90%和50%的分位点。 2.1.1 以起动次数为代表的载荷分散系数 某配装三代战斗机的11台份涡扇发动机在100~1 100飞行小时内的累积起动次数分布如图1所示。可以看出,随着飞行时间的增加,发动机累积起动次数的分散性逐步扩大。对每个时间段内11台发动机的起动次数进行三参数韦布尔概率分布拟合,以相关系数绝对值最大为目标进行优化,得到11台发动机在不同时间段内起动次数的韦布尔概率分布函数曲线,如图2所示。图3为对应分布函数的形状参数随飞行时间的变化曲线,可以看出,韦布尔分布的形状参数随着飞行时间的累积逐渐增大,并且增大的趋势随着飞行时间的增加逐渐趋缓。 图1 11台份某涡扇发动机100~1 100飞行小时内的累积起动次数 图2 11台份某涡扇发动机100~1 100飞行小时内发动机累积起动次数的概率密度函数 图3 11台份涡扇发动机起动次数分布的形状参数随飞行时间的变化 根据拟合的分布结果,由式(5)可以得到不同时间段内累积起动次数的分散系数及其变化趋势,如图4所示。可以看出: 图4 累积起动次数分散系数随工作时间的变化 1)各工作时间累积起动次数的分散系数在1.0~2.0之间。这也解释了MIL-E-87231、JSGS-87231A、JSSG-2007规定结构件最低低周疲劳寿命应为设计寿命的1~2倍的原因。 2)各工作时间累积起动次数的分散系数随着工作时间的增加逐渐减小。表明随着使用寿命的增加,起动次数的载荷分散度对结构件可靠性的影响越来越小。 2.1.2 大状态工作时间载荷分散系数 发动机的大状态工作时间是指发动机最大工作状态和加力工作状态持续的时间,主要表征了发动机的燃烧室、涡轮导向器、涡轮叶片以及涡轮机匣等热端部件的持久/蠕变损伤[18]。 11台发动机在20~990飞行小时内的累积大状态工作时间的统计数据分布如图5所示。可以看出,与起动次数呈现相似规律,即随着飞行时间增加,大状态工作时间的分散性也在逐步增加。同样地,采用三参数韦布尔概率分布函数进行同一时间段内不同发动机大状态工作时间分布规律的拟合,得到的韦布尔概率密度分布曲线分别如图6(a)和图6(b)所示。为了进行直观的比较,在图6(b)中也显示了飞行时间为400 h的大状态工作时间的分布曲线。从图6(a)中可以看出,当飞行时间较短时,发动机的大状态工作时间对飞行时间更加敏感,而随着飞行时间的增加,这种敏感性逐渐在降低。 图5 11台份某涡扇发动机在不同飞行时间内的大状态工作时间 图6 11台份某涡扇发动机不同飞行时间下大状态工作时间分布的概率密度函数系数 从图7的形状参数与发动机飞行时间的变化曲线可以看出,除去个别的点,形状参数总的变化趋势与起动次数分布曲线具有相似的趋势,即随着工作时间的加长,其形状参数逐渐变大。当发动机飞行时间低于400 h时,大状态工作时间分布的形状参数小于1.0,随着飞行时间的增加,分布的形状参数显著增加。 图7 11台份某涡扇发动机大状态工作时间分布的形状参数随飞行时间的变化 值得注意的是,飞行时间20~100 h的大状态工作时间分布的形状参数呈现无规律性,原因与新机训练初期各台发动机使用偶然性较大有关,也与仅限制发动机大状态总的工作时间,而在使用中没有具体要求有关。这种偶然性在图8的大状态工作时间的载荷分散系数的变化中也有明显体现。从图8中可以看出: 图8 大状态工作时间分散系数随工作时间的变化曲线 1)大状态工作时间随着累积工作时间的分散系数在1.0~2.0之间。 2)除了个别时间点外,大状态工作时间分散系数随着累积工作时间的增加逐渐减小,说明随着使用寿命的增加,大状态工作的载荷分散度对结构件可靠性的影响越来越小。 2.1.3 固定任务混频的寿命相关载荷分散系数 一般情况下,在航空发动机设计阶段使用固定任务混频的设计载荷进行零部件寿命评估,而在实际飞行中则以变任务混频载荷为主。研究表明[19],随着发动机工作时间的增加,固定任务混频和变任务混频的载荷参数累加值的分布特性较为一致,即都趋于正态分布。则在一定可靠度p下结构的载荷强度可以表示为 xp=μ+upσ (6) 式中:up为与累积概率相关的标准正态偏量;μ和σ分别为正态分布的均值和标准差。 固定飞行任务混频即固定的飞行任务集合、固定的飞行任务组合频比和每个飞行任务给定单一的飞行剖面载荷。该涡扇发动机载荷库中的载荷强度分布如图9所示,其中蓝色圆圈表示原始数据,蓝色曲线为采用正态分布拟合得到的曲线,红色曲线为采用三参数韦布尔分布拟合得到的曲线。载荷强度”是一个泛指的量:对于低周疲劳,指的是某一个飞行剖面所产生的当量标准循环数;对于陀螺力矩高周疲劳,指的是任务剖面的当量标准陀螺力矩循环次数;对于持久载荷,指的是剖面的当量标准状态持久寿命消耗时间;而对于蠕变载荷,指的是剖面的当量标准状态蠕变寿命消耗时间。可以看出,正态分布曲线和韦布尔分布曲线的差异很小,也即可以认为固定任务的载荷强度累积概率分布趋于正态分布。 图9 涡扇发动机载荷数据及其分布拟合曲线 假设飞机子样为1 000,采用蒙特卡洛方法模拟基于固定任务混频的飞行过程,得到一次典型飞行过程中累积剖面数从1增加到4 000过程中的累积载荷强度分布特征的变化,并得到相应分布的均值和标准差[20]。同样地,根据式(6)得到载荷分散系数随累积飞行剖面的变化曲线,如图10所示。可以看出: 图10 固定任务混频的载荷分散系数随累积飞行任务剖面的变化曲线 1)固定任务混频下,载荷分散系数除了在飞行任务剖面数很小的情况,大部分处于1.0~2.0之间。 2)载荷分散系数随着累积飞行任务剖面的增加逐渐减小。表明随着使用寿命的增加,载荷强度的分散性对结构件可靠性的影响越来越小。当累积飞行任务剖面数大于1 500时,载荷分散系数在1.03以下,此时,在进行结构件可靠性分析时,可不考虑载荷强度的分散性对结构件寿命的影响。 2.1.4 变任务混频的寿命相关载荷分散系数 相对于固定任务混频用在发动机设计阶段而言,每台发动机的实际使用历程中会依次历经第1, 2, …,n个任务混频,即发动机主要面对的是变任务混频载荷。基于该涡扇发动机的载荷库数据(见图9),基于文献[19]中给出的3种任务混频,采用蒙特卡罗方法得到1 000个飞机子样的变任务混频飞行过程,从而得到变任务混频条件下累积载荷强度随飞行剖面累积数的分布及其均值和标准差。同样地,根据式(6)可以得到变任务混频条件下的载荷分散系数及其随累积飞行任务剖面的变化规律,如图11所示。 图11 变任务混频载荷分散系数随累积飞行任务剖面的变化曲线 可以看出,变任务混频的载荷分散系数与固定任务混频载荷分散系数有相似的规律: 1)变任务混频下,载荷分散系数在1.0~2.0之间。 2)载荷分散系数随着飞行任务剖面累积数的增加逐渐减小。同样表明,随着使用寿命的增加,载荷强度的分散性对结构件可靠性的影响越来越小。当飞行剖面累积数大于1 500时,载荷分散系数在1.02以下,在计算时可以忽略。 从蒙特卡洛抽样的角度来看,不论是固定任务混频还是变任务混频,每台发动机需要抽样的样本点都等于每架飞机需要飞行的任务剖面数。当发动机的使用寿命较短时,等价于每架飞机的飞行剖面数就少,也即按照图9 的载荷强度累积概率密度函数进行抽样时所需的样本量较少,导致不同飞机发动机的载荷强度的分散性就较大,即发动机的载荷分散系数就较大。 当使用寿命逐渐增加时,等价于每架飞机的飞行剖面数在逐渐增多,也即按照图9的载荷强度累积概率密度函数进行抽样时所需样本点的数量在增加。因此,每架飞机发动机的载荷强度都在逐渐更加趋近于函数均值,即发动机的载荷分散系数就变得相应较小。 从以上的计算分析可以看出,每台发动机之间存在使用载荷的差异,这种载荷的分散性与使用规律和载荷性质均相关,表明在航空发动机的可靠性设计和服役过程中的监控的重要性。一般情况下,可以采用针对不同装机对象给定不同寿命指标、加装历程记录仪和采用修正的综合换算率控制等三种技术措施严格控制使用载荷分散性,保证零部件的安全使用。其中,航空发动机的综合换算率与飞行训练、地面维护特点、使用环境等密切相关,是一个需要经常调整的变化量。 影响发动机结构件疲劳分散性的因素可以归结为结构制造分散性和使用载荷分散性两类,从而提出与之对应的2种分散系数,即结构分散系数和载荷分散系数,并给出了载荷分散系数的定义和计算方法。基于对中国某涡扇发动机不同飞行时间和不同飞行任务剖面下相关载荷信息的分析,可以得到以下结论: 1)某涡扇发动机的载荷分散系数大多在1.0~2.0之间,并随着工作时间的增加呈现下降趋势,下降速率与载荷性质有关,并从侧面解释了美军标中规定的结构件最低低周疲劳寿命应为设计寿命的1~2倍的原因。 2)随着某涡扇发动机使用寿命的增加,累积载荷分散性对结构件可靠性的影响越来越小。当累积飞行任务剖面数大于1 500时,固定任务混频和变任务混频条件下的载荷分散系数非常接近1.0,在结构件的寿命可靠性评估中,可以忽略其影响。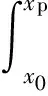
2.1 载荷分散系数


2.2 实际使用中控制载荷分散系数的技术措施
3 结 论
