基于损伤权重的混合多钉连接件疲劳寿命预测方法

张峻瑞,郑锡涛,*,袁林,钟贵勇,李国琛

1.西北工业大学 航空学院,西安 710072

2.西北工业大学 飞行器复合材料研究所,西安 710072

3.中航工业成都飞机设计研究所,成都 610041

随着复合材料在航空结构上的广泛应用,金属与复合材料混合多钉连接成为航空结构最常见的一种连接形式,飞行器结构破坏的60%～80%情况发生在连接处。当机械连接结构破坏时,最常出现的失效形式是连接接头的疲劳破坏。

前期研究表明,因为复合材料本身为各向异性,且存在分散性大、抗冲击损伤容限低等缺点,造成其疲劳特性与金属疲劳特性差别较大,因此适用于金属材料疲劳分析的方法通常不适用于复合材料的疲劳分析,也不完全适用于混合多钉连接结构。在交变载荷的作用下,复合材料的损伤不断累积,复合材料的疲劳易发生“突然死亡”现象,即疲劳失效前,宏观上没有明显征兆。

混合多钉连接结构的疲劳寿命受多方面因素影响,由于连接结构的破坏模式多样,因此在对构件进行寿命预测时,应按照材料特性划分,分别进行预测。金属材料的疲劳研究起源较早,在业内已经被广泛研究,试验方法也比较完善。而针对复合材料的疲劳问题,学者们也提出许多不同的研究方法,总体上可将其分为2类：试验方法及试验分析法。试验方法顾名思义,在此不再介绍,而试验分析法,又称疲劳寿命预测法,基本思路是根据复合材料单向层合板和典型铺层形式的层合板疲劳性能试验数据,结合相应的寿命预测模型来确定层合板的疲劳寿命。

由于结构失效是由损伤累积引起的,因此对疲劳损伤的准确预测就是对结构疲劳寿命的准确预测。在金属中常用的损伤累积模型包括Miner线性损伤累积模型、Manson双线性损伤累积模型和Chaboche连续损伤力学模型等。复合材料的损伤累积模型包括:以Miner线性损伤累积模型为基础,Mao和Mahadevan[1]建立了以幂函数组合形式表征损伤的经验模型；Plumtree和Shen[2]建立了以基体微裂纹饱和度为损伤衡量标准的损伤演化模型；Epaarachchi和Clausen[3]考虑材料塑形,联合剩余强度来考虑损伤累积。Wu和Yao[4]考虑了静强度分布对复合材料进行寿命预测。这些学者的目光聚集在材料本身的损伤上,而结构连接件的损伤又与材料本身的损伤存在一定的差别。

刘建明等[5]单从复合材料层合板的疲劳寿命出发对复合材料单钉连接结构进行寿命预测。Mariam等[6]对单搭接接头在应力比R= 0.1、不同应力水平下的拉伸剪切疲劳性能进行了试验研究。Hart-Smith[7]则经大量试验研究后,认为层合板接头铺层比例大小直接影响到其结构静载失效模式。Yan[8]和Kretsis[9]等研究了拧紧力矩对层合板接头静强度的影响。Kam[10]针对不同的紧固件装配方法,来研究不同装配方法下连接件的失效模式。学者们仅仅对不同工况下的失效模式进行了分析,并没有一个较为完备的疲劳寿命预测手段[5]。

针对现有混合多钉连接结构疲劳寿命预测方法单一、精度低的问题,本文基于Miner准则,考虑连接结构中金属紧固件部分以及复合材料连接板部分的损伤权重提出一套适用于工程应用且精度较高的疲劳寿命预测方法。

1 混合多钉连接件疲劳寿命预测模型

金属与复合材料混合多钉连接件的损伤主要集中在连接处,通过对混合多钉连接件疲劳失效状态进行观察,可见连接处的螺栓孔损伤,如图1所示。与传统的Ⅰ型、Ⅱ型断裂不同,其损伤状态是多种模式耦合的。其中主要包括螺栓的断裂和螺栓孔处复合材料的分层损伤以及复合材料的基体损伤和纤维损伤。而判断结构失效中,并不是传统意义上的部件失效整体结构就失效,而是需要综合考虑金属连接件与复合材料连接板各自的失效形式。

图1 混合多钉连接件螺栓孔附近的损伤

结构失效的判断依据通常来源于对结构损伤的分析。在分析混合多钉连接的损伤时要考虑紧固件的损伤、复合材料层合板的界面脱粘损伤以及复合材料的基体损伤和纤维损伤。随着循环加载,上述损伤也逐渐发生,但是由于材料属性的不同、复合材料的铺层数量、铺层方向不同、螺栓孔分布位置不同等多方面因素,这些损伤演化的速率也完全不同。复合材料本身的损伤演化流程中[11],分层损伤是由于基体中裂纹耦合到界面使界面发生脱粘而产生的复合效应。因此在损伤预测中可将复合材料的分层损伤作为表征量来判断复合材料单元是否破坏。从而可以将复合材料损伤中各种形式的损伤作为一个整体的分层损伤Db,牺牲一部分精度来提高计算效率。

传统理论认为结构的寿命是根据“短板理论”得到,即当结构中任意一个部件预测损伤值达到1时所对应的寿命就是结构的整体寿命。因此通常结构的预测寿命值是小于实际寿命值。当不需要区分破坏形式仅从寿命角度进行讨论,就可以单从损伤量的角度出发,考虑各部件损伤权重,进而对结构的疲劳寿命进行预测。

根据文献[12]对混合多钉连接件的描述,混合多钉连接件主要由复合材料连接板、金属连接板、紧固件、加强片组成。而连接件的主要失效原因是紧固件发生破坏,因此混合多钉连接结构中依据“短板理论”,当紧固件的损伤值达到1时试验件已经发生了破坏。然而事实上复合材料连接板在这个时候还并不是完全损伤的状态,根据试验数据[13]可以得知,在紧固件破坏的时候,复合材料仅在螺栓孔处发生分层现象,大部分区域仍处于基体微裂纹开裂的损伤初始阶段。那么即使紧固件发生破坏,复合材料连接板也对整体结构有一定的支撑作用。但是由于复合材料对开孔比较敏感,紧固件仍在结构承载中占主要部分。因此可以根据试验数据[12,14]写出以下经验公式：

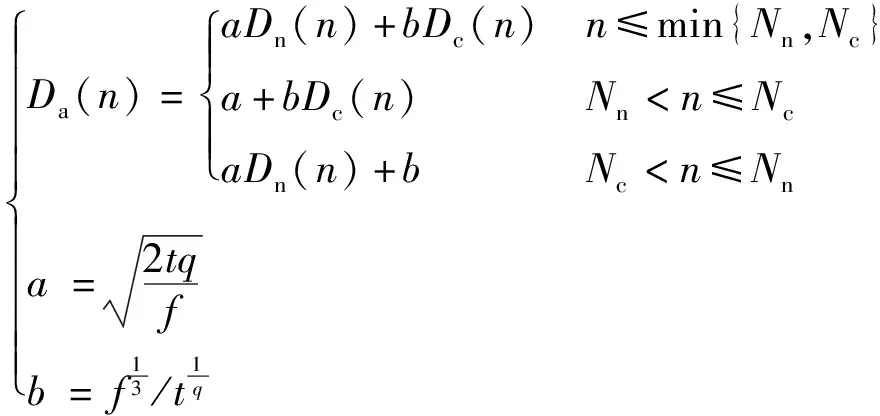
(1)

式中：Da为结构整体损伤,随着加载次数n值的变化而变化,当Da值为1时认为结构整体失效,这时的n值即为预测的结构无损寿命；Dn、Dc分别为紧固件损伤和复合材料分层损伤,其值来源于Miner理论,即Dn=n/Nn和Dc=n/Nc,其中Nn、Nc为紧固件和复合材料连接板的无损寿命,可以通过模拟试验获得；a和b为损伤权重值,根据紧固件分布以及复合材料层合板铺层数量得出；f、q、t分别为复合材料层合板的铺层数、紧固件的列数、紧固件的排数,其取值均为正整数。

2 混合多钉连接损伤模拟

为求得紧固件和复合材料连接板的无损寿命,本文设计复合材料连接板材料为ZT7H/QY9611碳纤维增强树脂基材料,铺层方式为[45/0/-45/90/0]4s,其厚度为5 mm,金属带板材料为30CrMnSiNi2A,其厚度为9 mm,紧固件材料为 Ti-6Al-4V钛合金,其螺柱直径为6.35 mm,以进行模拟试验。两侧采用玻璃钢(FRP)材料作为加强片,采用图2设计的试验件尺寸进行建模,其材料参数[13，15-16]如表1和表2所示,其中：E为弹性模量；G为剪切模量；ν为泊松比；X为沿纤维方向(1方向)的强度；Y为垂直纤维方向(2方向)的强度；3方向为垂直于层合板的方向；S为剪切强度；下标“T”表示拉伸,“C”表示压缩。

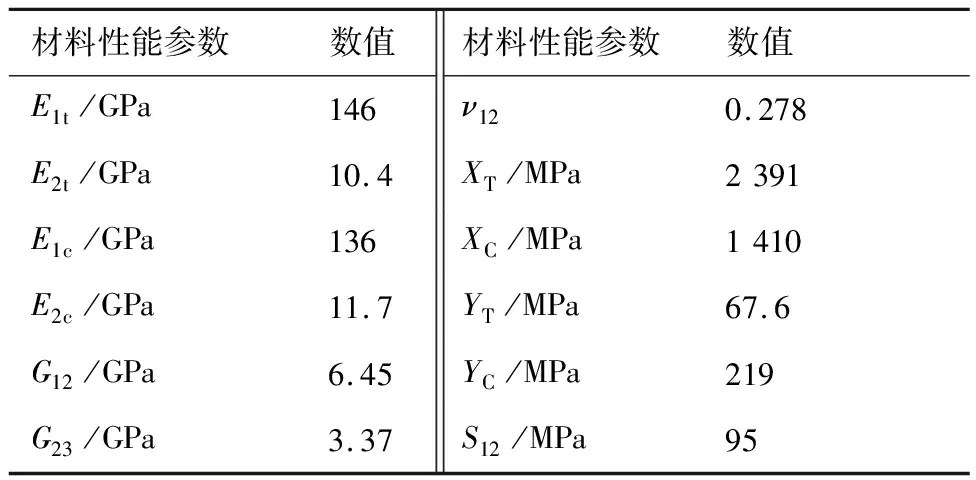
表1 ZT7H/QY9611材料参数

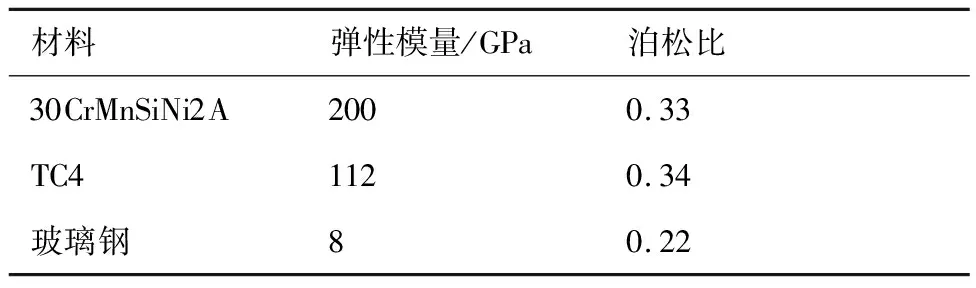
表2 连接件金属与玻璃钢材料属性

图2 混合多钉连接件设计

通常的疲劳模拟流程可以概括为以下几点：应力分析、单元失效判断、性能退化、结构失效判断。基于以上流程开发了一套基于Abaqus模拟软件使用的子程序来进行疲劳模拟。Umat子程序流程如图3所示。其中复合材料单元失效采用

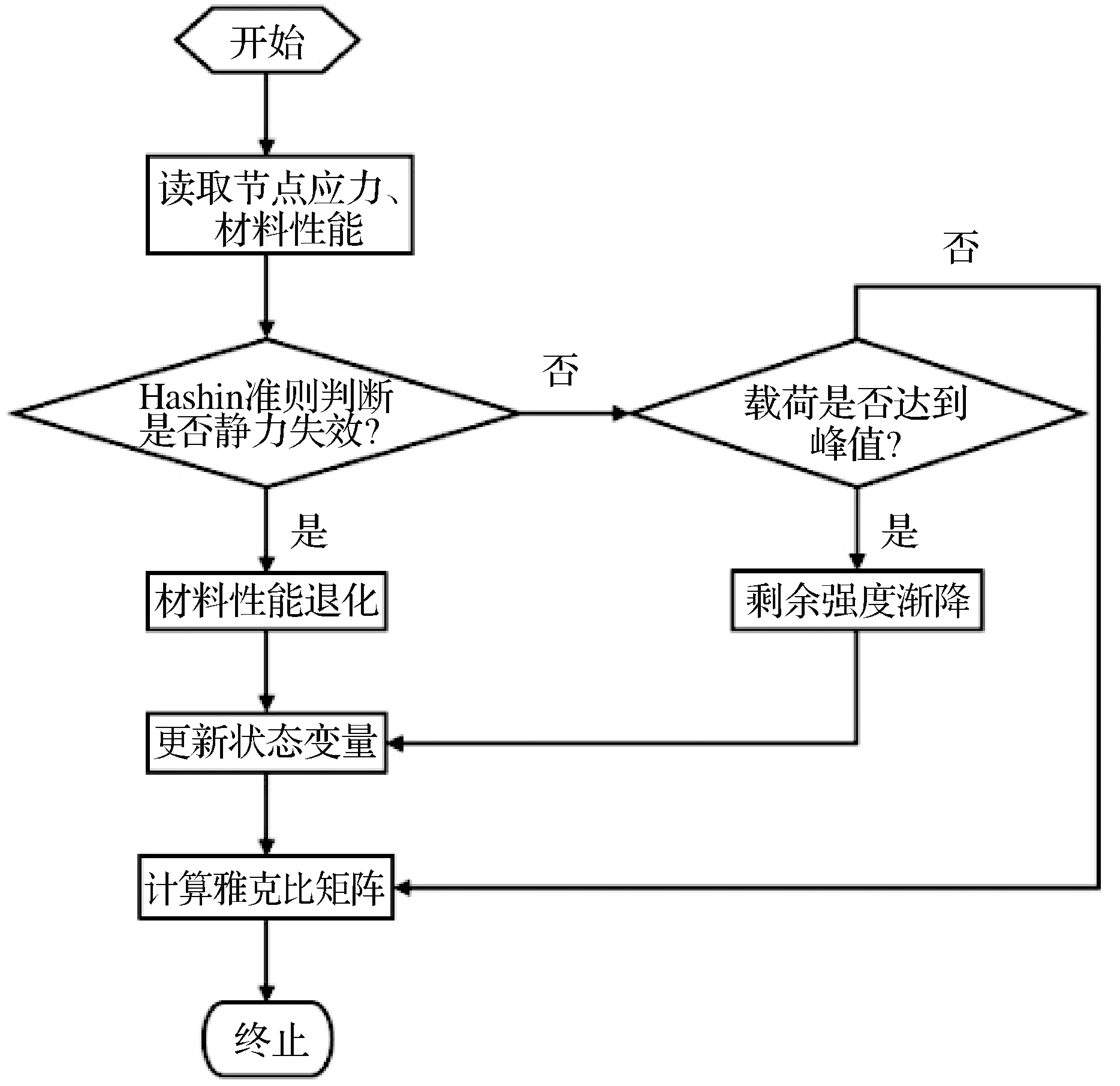
图3 Umat子程序流程

的是Papanikos改进的三维Hashin准则[17-18],如式(2)～式(8)所示,金属材料单元失效则使用最大应力准则,材料性能退化方法采用直接退化法。

纤维拉伸失效判据(σ11>0)：

(2)

纤维压缩失效判据(σ11<0)：

(3)

基体拉伸失效判据(σ22>0)：

(4)

基体压缩失效判据(σ22<0)：

(5)

纤维基体剪切失效判据(σ11<0)：

(6)

法向拉伸分层失效判据(σ33>0)；

(7)

法向压缩分层失效判据(σ33<0)：

(8)

式中：σ11、σ22、σ33为各方向正应力；τ12、τ13、τ23为各方向剪应力;ZT、ZC为铺层法向拉伸、压缩强度。

由文献[19]中静力试验结果可知,靠近金属的复合材料的损伤最为严重,因此将模型简化,忽略钉帽斜削角的影响,同时在建模时,将刚性垫片与连接件共同建立出来。由于试验件复合材料部分为对称铺层,且试件整体的几何尺寸和边界条件在试件宽度方向上对称,故根据试验件尺寸建立1/2模型以节约计算时间。本文复合材料层压板和紧固件均采用三维实体模型,依据材料厚度将复合材料层合板模型在厚度方向上进行划分,模型各零件之间设置通用接触。为进一步提高计算效率,以及降低模型不收敛的风险,并且考虑到应用损伤权重，对复合材料层合板和紧固件分别建模。在以多钉连接结构中复合材料部分作为主要研究对象,进行损伤分析时,可以采用将紧固件与金属板绑定建模的方式使模型进一步简化,如图4所示。

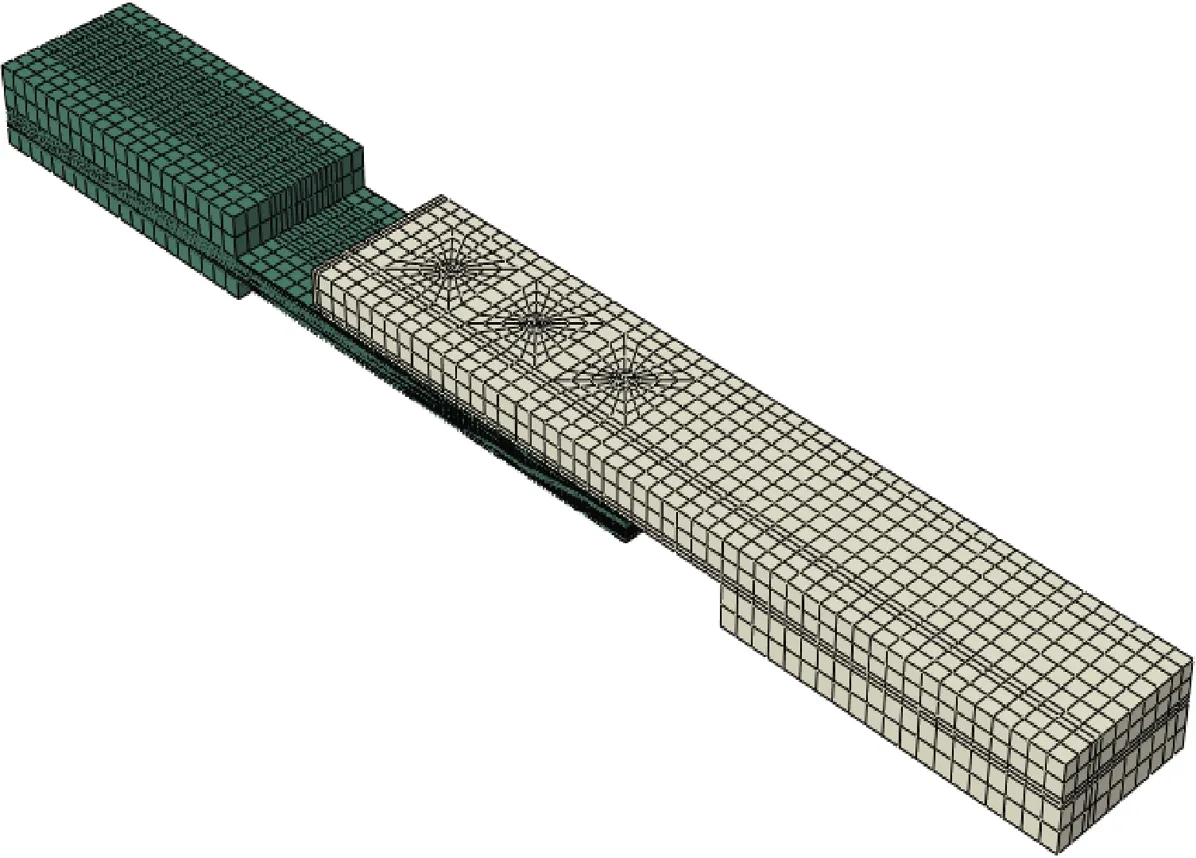
图4 连接结构简化示意图

此时,每个接头区域减少2个接触对,网格类型和布种形式保持不变,模型总体单元数量变为90 374。用同样的方法对紧固件建模,为获得更为安全的紧固件疲劳寿命,采用图5所示模型,对紧固件进行受力分析。由于在复合材料孔边各部件的受力情况复杂,且材料出现Ⅱ型裂纹的条件极为苛刻,故本文假设紧固件将发生Ⅰ型断裂,即紧固件产生的裂纹由局部拉应力引起并使得紧固件断裂,根据文献[20]中给出的Ti-6Al-4V材料的室温轴向加载高周疲劳应力-寿命曲线,计算紧固件高周疲劳寿命,其等效应力寿命表达式为

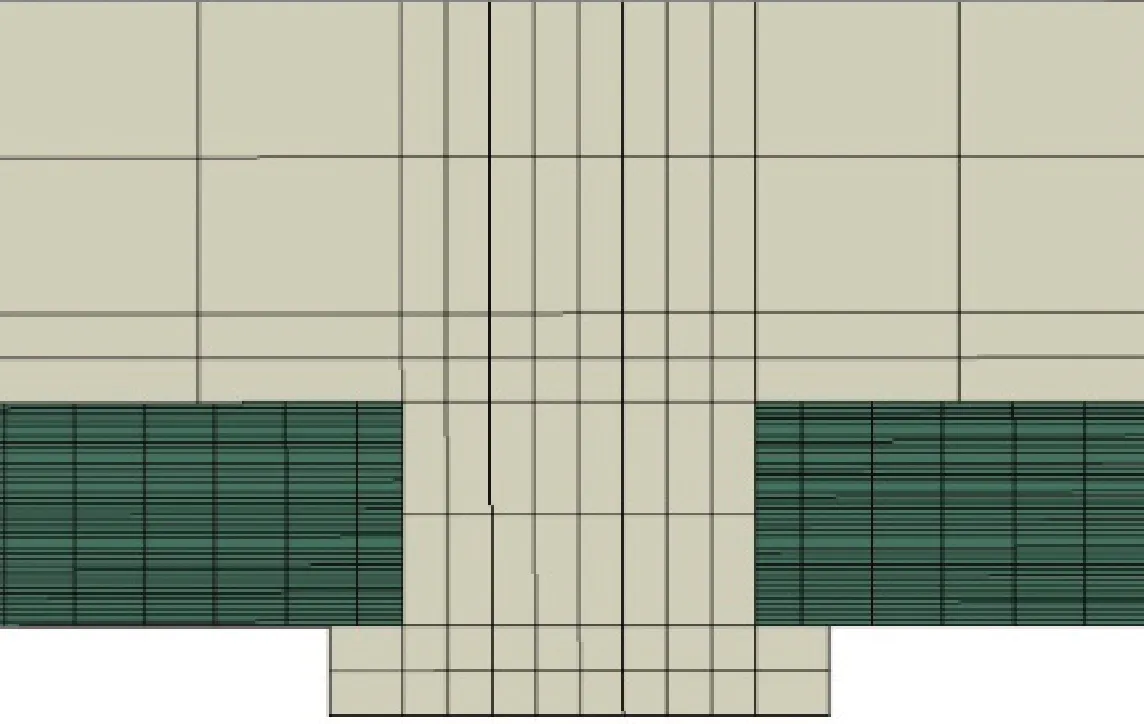
图5 接头剖面单元网格划分

lgN=16.64-4.76lg(σeq-346)

(9)

σeq=σmax(1-R)0.45

(10)

式中：N为某应力水平作用下破坏对应的循环数；σeq为等效应力；σmax为交变应力最大值。

为获得紧固件局部轴向应力,本文选用结构受最大压缩载荷作用下,紧固件的最大主应力值作为寿命计算中的σmax,读取对应节点在结构受到峰、谷值载荷作用下的最大主应力。

本文采用随机载荷谱对混合多钉连接件进行加载,计算过程按照最大载荷不同分为8级并进行不考虑加载次序的分步计算。其中紧固件的损伤值通过式(9)和式(10)计算紧固件在各级疲劳载荷作用下的无损疲劳寿命,再由Miner线性损伤累积准则计算获得；复合材料的损伤值通过上述模拟方法计算获得其无损寿命,再根据Miner准则即可求得。求得的混合多钉连接结构在随机谱下的损伤分布情况如表3所示。

表3中紧固件在高载部分由于形变强化、裂纹尖端钝化、以及残余压应力等一系列影响会对材料产生一定的强化,从而会出现其疲劳寿命提高的现象。

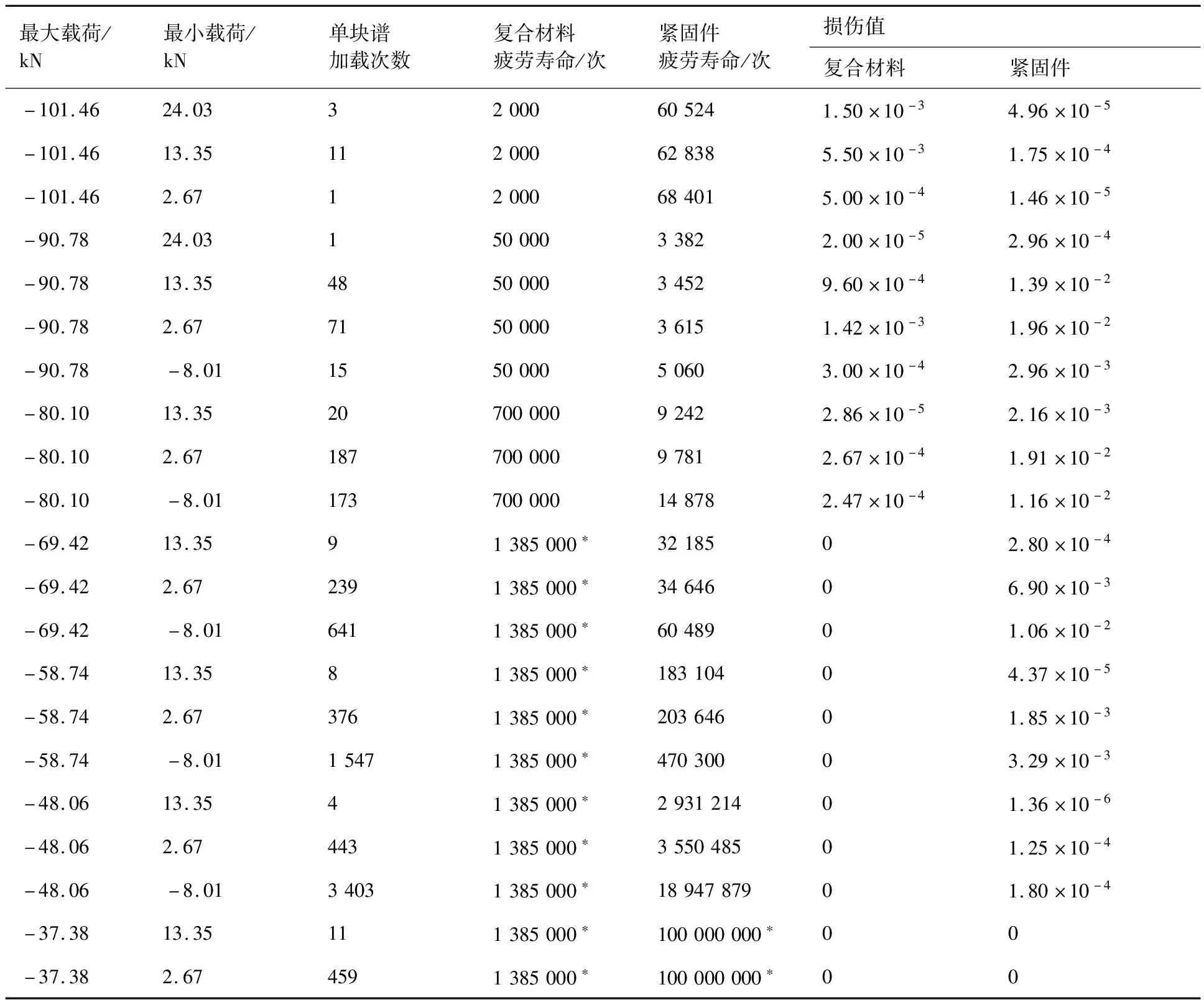
表3 最大载荷为101.46 kN时受谱载作用下的疲劳寿命及损伤分布

根据模拟结果可以将损伤累积过程表示成如图6所示。分别得出紧固件的无损疲劳寿命为78 900次循环,复合材料连接板的无损疲劳寿命为713 970次循环。本文采用的是每个载荷谱代表1 000个飞行小时的载荷谱。因此可以根据模拟试验的结果得出,复合材料连接板板的寿命为93 085 h,紧固件的寿命为10 288 h。由于本文采用的模型中紧固件分布为三排两列,复合材料连接板铺层为40层。因此可令式(1)中的t=3,q=2,f=40,从而得到

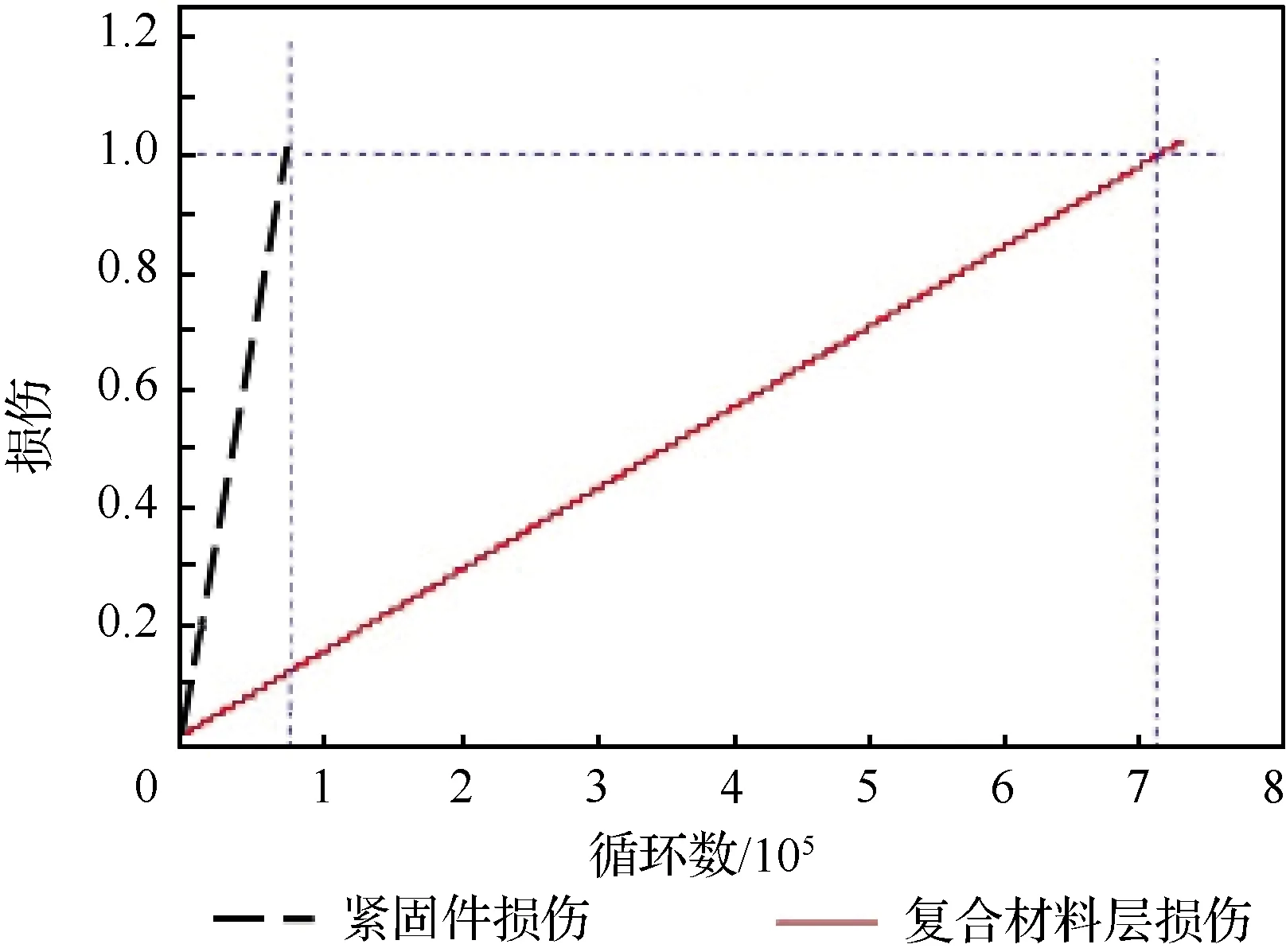
图6 损伤值的累积

Da(n)=

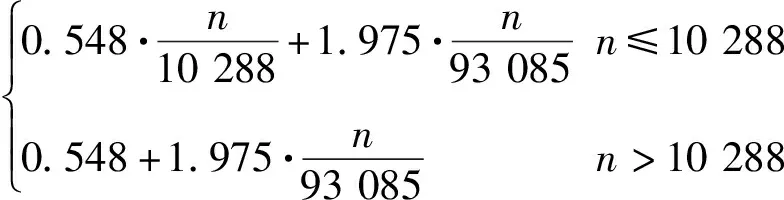
(11)

当Da(n)=1时,可以求得最终的预测寿命,即n值为21 303.5 h。

3 试验验证

3.1 试验过程

金属与复合材料混合多钉连接结构静力试验和疲劳试验均在INSTRON 8802液压疲劳试验机上完成。试验机量程为±250 kN,加载精度为设定值的±5%,试验环境为室温/干态。共进行了10件混合多钉连接试验件在随机载荷谱下的疲劳试验,其中4件进行C扫描分层损伤探查。在实际工况中,试验件主要受压缩载荷,为防止试验件在试验过程中因弯曲而被破坏,在试验机夹头的一侧增设了刚性垫片,以保证复合材料层合板与金属板的接触面和试件受载中面重合,从而降低受载弯矩。同时设计了点面接触防弯夹具,夹具与装夹示意图如图7所示。

图7 防弯夹具与装夹示意

3.2 试验结果分析

在试验完成后,得出各试验件的疲劳寿命以及观察到的损伤模式,如表4所示。

试验结果分散性较大,试验件失效形式主要仍是以紧固件断裂为主、以复合材料的破坏为辅。肉眼观测试验件损伤模式发现,一部分试验件出现紧固件和复合材料层合板同时断裂而另一部分则仅发生紧固件断裂,复合材料部分无明显的可见损伤,如图8所示。明显可以看出其中有一部分偏差较大的数据。因此利用统计学,通过离群检验可以排除FB02与FB08的值。将处理后的试验数据与模拟试验的预测结果进行对比分析,可得表5。可以看出考虑损伤权重的疲劳寿命预测对数误差为1.1%,而不考虑损伤权重的疲劳寿命预测对数误差为8.4%。由此可见考虑损伤权重的疲劳寿命预测精度有所提高。

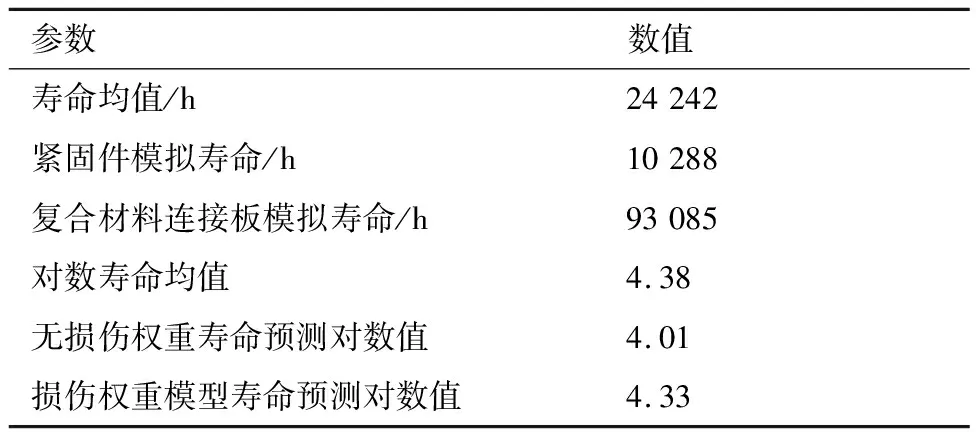
表5 载荷谱试验结果与预测结果

图8 载荷谱试验试件失效形式

为进一步探究复合材料的损伤模式,将复合材料进行C扫描测试,期望找到复合材料层合板的分层损伤起始时间。通过测试可以得出表6。根据表6不难发现虽然试验件的失效模式都是紧固件破坏后导致载荷重新分配进而导致整个结构失效,然而实际上在结构发生破坏前,试验件就已经发生了分层损伤,因此虽然是紧固件破坏导致了整个试验件的失效,但是由于复合材料损伤吸能的过程中会减缓紧固件的损伤。因此可以认为考虑损伤权重,引入复合材料的损伤来进行连接件的寿命预测是合理的,也是更加准确的。

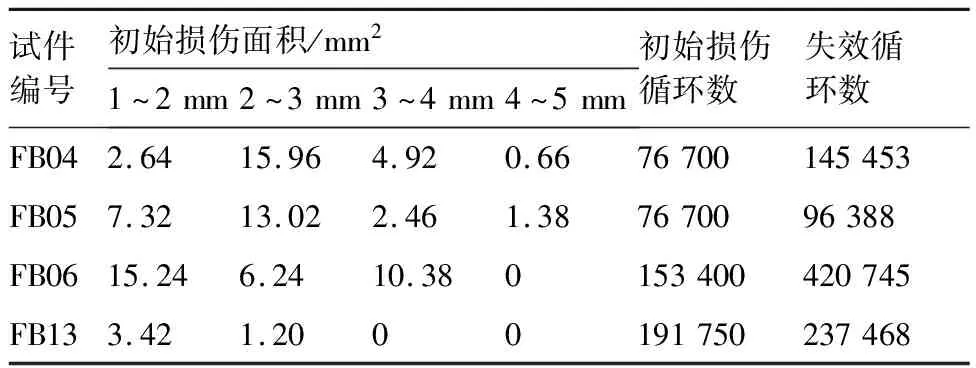
表6 不同厚度下各试件初始损伤面积

图9为FB13扫描结果。图中有6个螺栓孔,显示为白色,表示为无法接收反射信号,最浅色区域表示该位置没有损伤,其他代表着该区域有分层,由表面分层到底部分层,检测结果由黑至最浅色变化。对每次所得结果进行聚类分析,即可得到不同厚度下的损伤面积。

由图9可以看出,试件FB13复合材料层合板的损伤主要出现在螺栓孔附近,且集中在结构受压缩载荷作用的区域。可以观测到随着加载次数的增加,螺栓孔附近的损伤面积在增大。结合试验件的破坏模式,认为在初始损伤出现前,螺钉首先发生塑性变形,结合对螺钉位置进行标记的手段同样发现螺栓孔发生了一定角度的偏转,可以认为在加载过程中螺钉变形后与复合材料进行相互挤压,复合材料给予螺钉约束,阻止其进一步变形,而复合材料由于螺钉的变形挤压,在螺栓孔处发生应力集中而导致分层损伤的出现。同样证明了混合多钉连接结构的失效是复合材料连接板和紧固件的耦合作用。

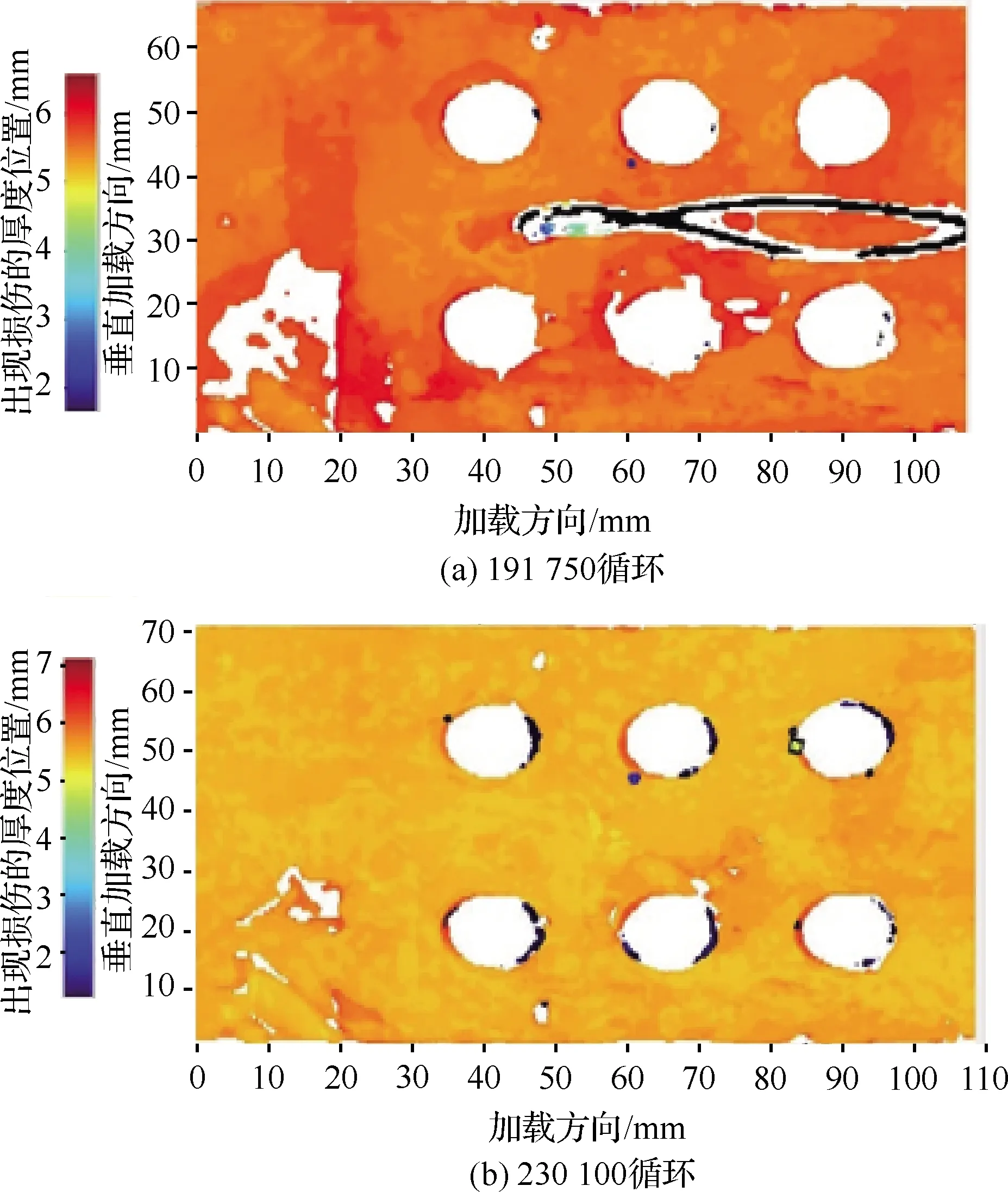
图9 FB13扫描结果

4 结 论

本文考虑混合多钉连接件各部件的损伤权重,通过建立模型、模拟分析、试验论证的方法对其疲劳寿命开展研究,得出以下结论：

1)本文提出了金属与复合材料混合多钉连接件的疲劳寿命预测模型。通过考虑紧固件的分布以及复合材料层合板的铺层数量,再分别结合紧固件与复合材料层合板损伤累积速率的不同给出各自的权重。并通过数值模拟、结合随机载荷谱下的疲劳试验,以及过程中的C扫描探测手段观测复合材料的分层损伤,进一步验证了此模型的合理性与准确性。

2)将试验结果分别与考虑损伤权重的预测手段和不考虑损伤权重的预测手段之间的误差进行对比。可以求得考虑损伤权重的预测对数误差仅为1.1%,其偏差主要来源于应力水平、加载频率、试验环境等诸多因素。相比不考虑损伤权重得到的8.4%的预测误差来说,考虑损伤权重大幅提高了预测精度。为金属与复合材料混合多钉连接件寿命预测提供了一种新的预测方法。