一种调频连续波阵列雷达的软件校准方法
2021-06-16赵中兴郑文文
完 诚,赵中兴,张 磊,郑文文
(中国船舶重工集团公司第七二三研究所,扬州 225101)
0 引 言
调频连续波(FMCW)阵列雷达是否能够满足探测性能,主要取决于接收通道校准的准确程度。雷达前端所使用的压控振荡器一般具有非线性波形,因此需要空间和时间校准以补偿压控振荡器(VCO)的非线性以及阵列接收通道之间的相位、幅度和时延差异。
对于FMCW雷达中的线性调频波形,VCO的非线性会使接收信号存在寄生调相[1],从而影响阵面方向图的主副瓣,解决该问题的软件方法包括调整非线性发射信号使其与已知基准相匹配[2],或者使用易实现但计算量较大的非均匀重新抽样技术[3]。本文提出了一种根据非线性调频信号精确建立非线性模型的新方法,通过确定非线性波形特性并将逆波形发送至VCO,这样可将输出调整为线性,从而实现非线性信号的校准。就阵列校准而言,天线线阵中不同的延迟和幅度可引入中频信号的幅度和相位偏移,从而极大地影响了天线方向图。
本文描述了一种软件校准方法,利用线性FMCW的信号特性,在较大宽带内改善雷达的空间和时间性能。第1章节提出了具有非线性VCO效应和空间误差的FMCW阵列雷达模型,第2章节探讨了时间和空间校准流程,第3章节基于某型X波段FMCW阵列雷达模型仿真验证了所提出方法的有效性。
1 校准信号建模
理想的FMCW雷达发射信号是线性调频信号,其频率随时间以斜率为K=B/T0线性增加,其中B是信号带宽,T0为调频持续时间。然而实际VCO会产生非线性相位噪声n(t),最终的射频波形可以用复数形式表示为:
s(t)=ej(2πf0t+πKt2+n(t))
(1)
式中:f0表示起始频率。
对于静止目标的雷达回波,在进行I/Q解调之前的线性调制信号回波总时延由两部分组成:回波延迟α以及第m个天线与本振通道间不等长电缆带来的延迟τm(雷达为等长电缆lm)。接收信号的幅度Am也随着电缆长度衰减。因此,第m个通道的单个点目标的中频信号可以由下式得出:
rm(t)=Amej(2πf0(t+α+τm)+πK(tα+τm)2)+n(t+α+τm)×
e-j(2πf0t+πKt2+n(t))=
ej(ωα(t+τm)+ωmt+φα+φm+φ(t,α+τm))
(2)
式中:ωα=2παK;φα=2πf0α+πα2K;ωm=2πτmK;φm=2πf0τm+πτm2K;φ(t,α+τm)=n(t+α+τm)-n(t)。
对线性调频阵列雷达接收阵列进行时间校准的主要目的是消除非线性相位偏移n(t)引起的主瓣衰减和副瓣抬升,空间校准的目的是减小由不同通道时延τm和幅度引起的阵列方向图失真。
2 校准算法
2.1 时间校准
若考虑在发射调频波形之前应用静态数字开环校准法去掉式(1)中的n(t)以获得线性频率输出,即假定在常温下用该方法测量VCO的电压频率曲线并存储相对于每个频点的电压,插入测得的电压频率曲线并在等距频率步进时重新抽样,获得线性扫频时的校准抽样电压点,然而该方法难以精确测量电压频率曲线,不能直接用于基于快时间雷达输出的发射信号,这里提出了一种动态数字闭环校准法。
动态闭环校准的目的是直接根据中频信号精确估算出非线性电压频率曲线。首先应用N项多项式对VCO发射信号的时变相位进行建模:
s(t)=ej(s1t+s2t2+s3t3+s4t4…+sNtN)
(3)
式中,s1=2πf0;s2=πB/T+s′2,则时延为τ的中频信号为:
y(t)=s(t-τ)s*(t)=
ej(s1(t-τ)+s2(t-τ)2…+sN(t-τ)N-s1t-s2t2…-sNtN)=
ej(b1+b2t+b3t2…+bNtN-1)
(4)
令s=[s1,s2,…,sN],b=[b1,b2,…,bN],则系数矢量s和b的关系式可以表示为:
b=A(τ,N)s
(5)
式中:A为时延τ和多项式阶数N的函数的N×N矩阵。
若N=4,矩阵A表示为:
(6)
其中τ的更高阶项数值相对较小。因此,矩阵A和相应的b都与τ成正比,发射系数s可由下式计算得出:
s=A(τ,N)-1b
(7)
通过公式(6),时间校准流程如下:首先,通过发射机和接收机之间的延迟电缆来获得训练数据,作为闭环测试。对多个调频信号求平均值以提高信噪比(SNR),并用Savizky-Colay平滑滤波器消除噪声。对于已知的N,应用最小二乘法多项式曲线拟合来估计重频相位矢量b,将脉冲重复周期归一化为1 s,以避免冗余计算。通过计算相位信息的平均斜率可以大致估计出时延,从而形成矩阵A。考虑到初始相位偏移在-π~π之间,起始频率的s1不会影响之后的重新抽样,所以仅用b和A的2~N阶数据来估计s,表示为s2~sN。如上所述,b与τ大致成正比,因此重新抽样结果不受τ影响,可以根据实际情况将式(7)最小化求出精确的τ:
(8)
式中:B表示实际线性调频带宽。
只要发射时将“逆”波形发送至VCO可通过非均匀重新抽样建立以下关系式:
(9)
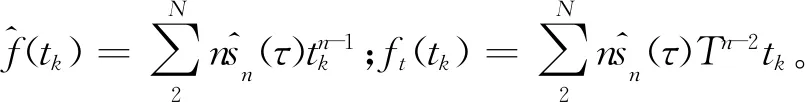
2.2 空间校准
由于天线线阵中不同通道的延迟和信号衰减会导致中频信号的幅度和相位偏移[4-6],空间校准的目的是补偿式(2)中的τm相关项,即频移ωmt、相变φm和ωατm。本文基于双延迟宽带波束形成法以实现宽带空间的校准。
假定已经进行了时间校准,即可以省略式(2)中的非线性项φ(t,α+τm),空间校准方法的第一步是补偿ωmkT和φm。在闭环试验期间,通过低相位噪声同等长度的延迟电缆中回波延迟是相同的。确定其中—个电缆延时为τr的基准通道,并比较频率剖面波峰间(即频率ωα+ωm和ωα+ωr间)的频差可以计算出电缆延迟差Δτm=τm-τr,这2个频率与延迟差成正比。相似地,幅度比γm=Aγ/Am可以根据上述2个波峰上的峰值得出。另一方面,鉴于中频信号的相位斜率与时延成正比,比较第m条信道和基准信道间的平均相位斜率差,也可直接计算出Δτm。这样校准项Θm(t)就可通过下式得出:
Θm(t)=γme-j(ωΔmt+φΔm)
(10)
ωΔm=2πτΔmK
(11)
(12)
将校准项应用于重新抽样非线性调频信号,利用基准通道分别通过频移和相移校准式(2)中的τm相关项ωmt和φm:
rm(t)×Θm(t)=Arej(ωα(t+τr+Δτm)+φα+φr+θm)
(13)
ωr=2πτrK
(14)
(15)
θm=πτrτmK
(16)
对于一般调频连续波雷达,τrτm相当于ns2,与K相比较小,因此通常可忽略相变θm。由于到达延迟未知,因此根据非线性调频波形很难校准与ωαΔτm相关的式(13)中的通道间相变。基于傅里叶变换的时移定理,可以在脉冲压缩后对该项进行校准。应用持续时间为T0的矩形窗,式(13)中的傅里叶变换可表示为:
(17)
为消除延迟差Δτm产生的式(17)中的最后一项,必须将频率补偿用于式(17),作为第2延迟,该频率补偿为ej(ωΔτm)。
频域校准信号的最终表达式可写为:
该式与通道数m无关且各通道无差别。实际上,在雷达的到达延迟相对小的情况下也可忽略偏差ωαΔτm,因此,对校准雷达第2延迟补偿非必须。空间校准方法框图如图1所示。

图1 空间校准方法框图
综上所述,空间校准步骤可概括如下:
(1) 对线性调频连续波雷达接收阵列进行闭环试验。选择1个基准通道,通过比较两通道间频率曲线峰值处的频率和幅度信息,可以获得通道误差延迟Δτm与γm幅度差值。
(2) 将上一步中得到的Δτm和γm代入式(10)中,并将其应用于时间校准数据集,从而得到式(13)。
(3) 略去相变项θm,将第2延迟频率补偿算式中的频域相位叠加至式(17)中的各通道FFT输出。
3 仿真与实验分析
为评估校准方案的可行性,对基于天线线阵间隔为18 cm的16通道X波段线性调频连续波雷达接收阵列进行仿真评估。雷达的技术指标设置如下:扫频为9.275~9.575 GHz,抽样率为82.5 KS/s,脉冲重复频率为120 Hz。为验证2.1节的时间校准,利用静态数字开环校准法与动态数字闭环校准法2种校准方法对VCO的非线性度进行仿真比较。为评估线性化性能,将非线性程度(DON)定义为经校准的(相对于理想相位)和未校准的信息均方误差的百分比:
(18)
如图2所示,未校准重频信号的DON为100%,如图3所示,静态数字开环校准法校准后的DON为26%,图4表明了动态数字闭环校准法的性能,其DON降至0.05%。在图5中,模拟2个相邻固定目标,分别应用动态数字闭环校准法和静态数字开环校准法对距离分辨率进行了仿真比较,应用动态数字闭环校准,发射方向图波峰更窄,距离波门内信噪比有效改善,距离分辨率明显提高。
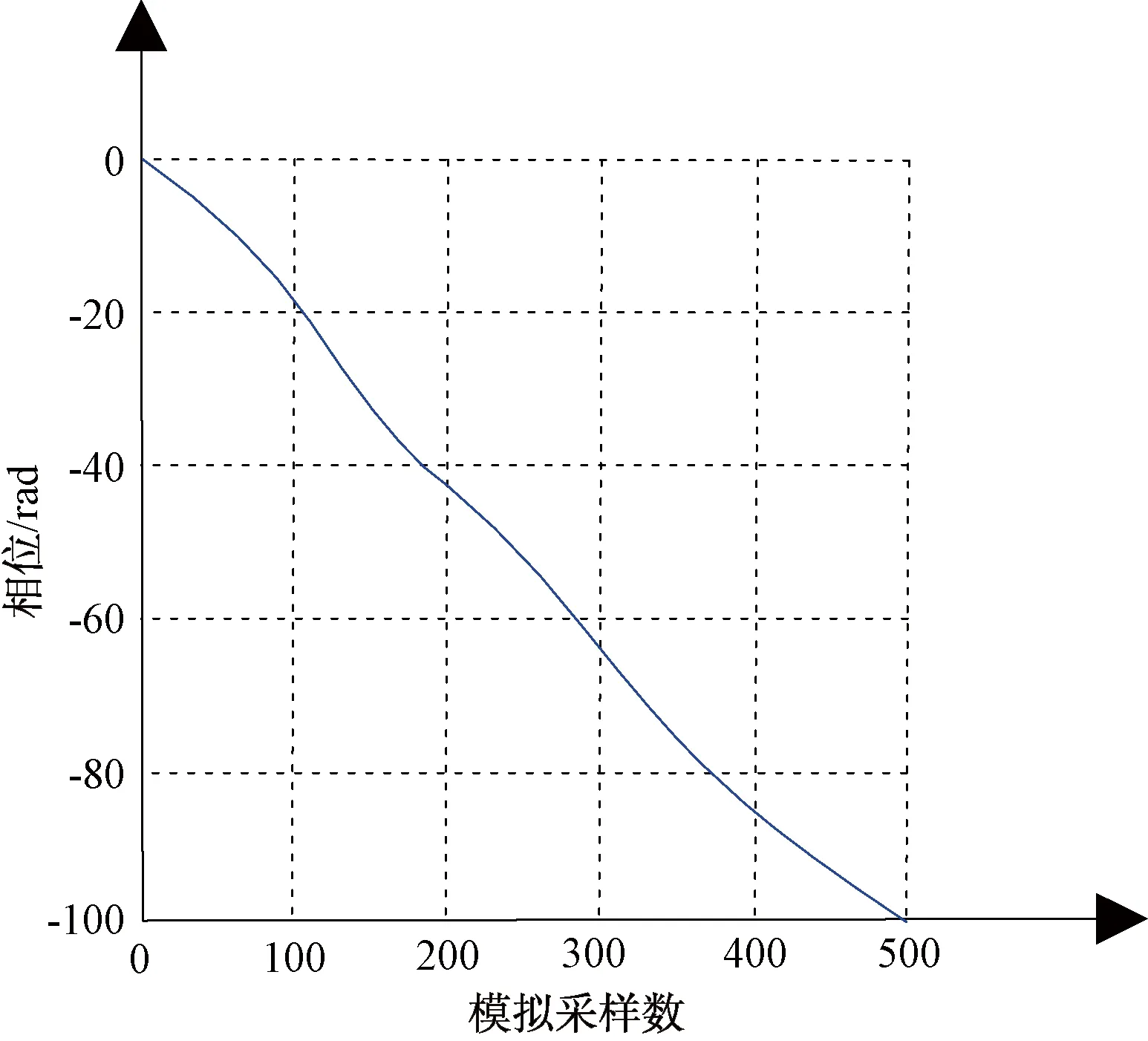
图2 未校准重频信号
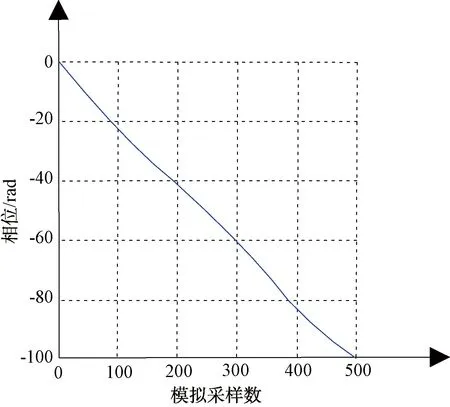
图3 静态数字开环校准法
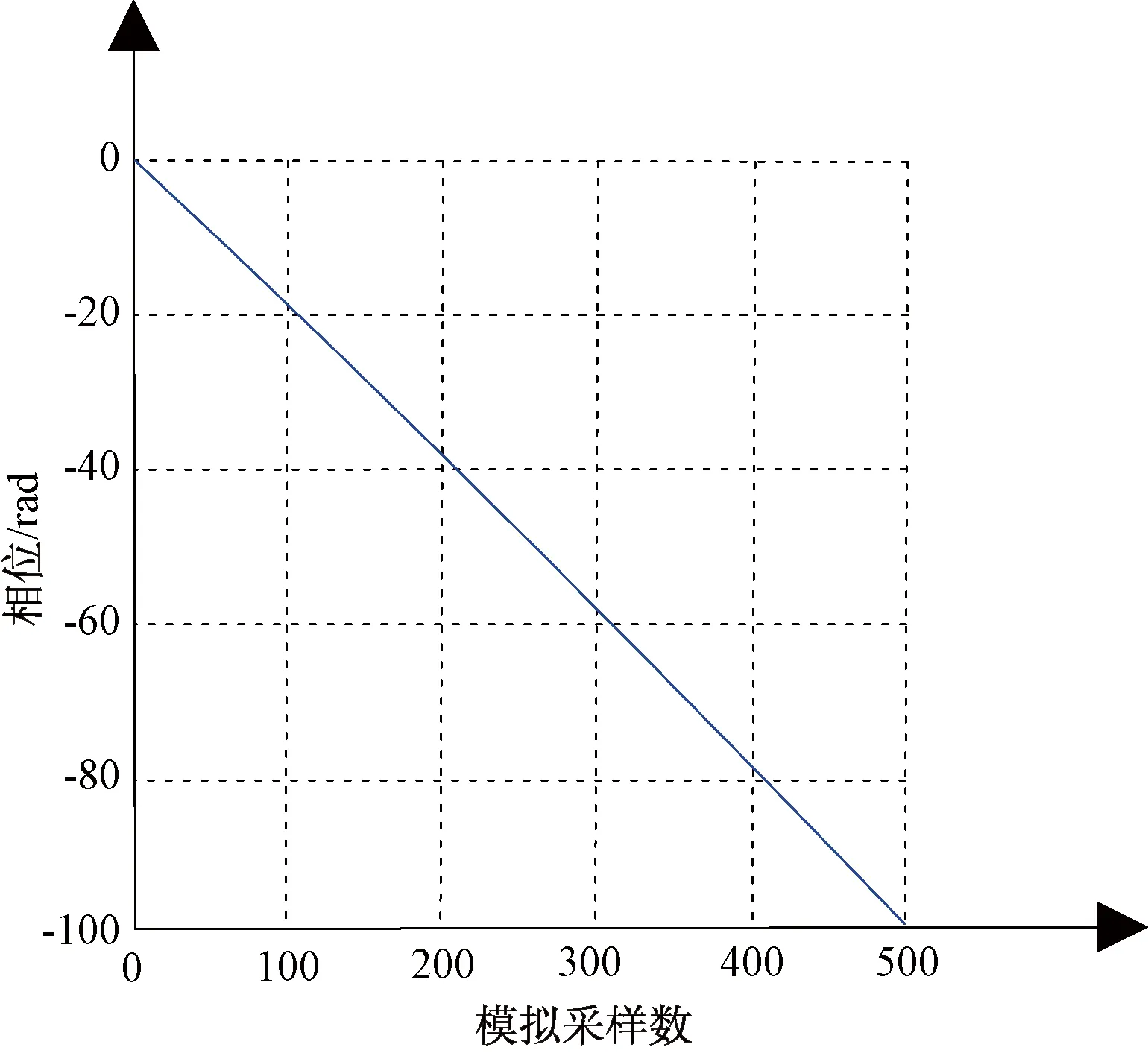
图4 动态数字闭环校准法

图5 开环与闭环校准的距离分辨率对比图
通过测试接收阵列的接收天线方向图验证电缆延迟的空间校准。为测量阵列方向图,将发射源置于离接收阵面22 cm的扫描架。图6表明了接收波束合成后的天线方向图,其中曲线2表示软件校准后天线方向图,曲线3表示未校准天线方向图,曲线1为假设各通道与基准信道均相同的理想仿真曲线。从图6可以看出,校准前天线副瓣为-20.3 dB,空间校准后的天线副瓣为-28.1 dB,经过校准的方位图主瓣和副瓣性能相对于未校准阵列有了显着的改进。
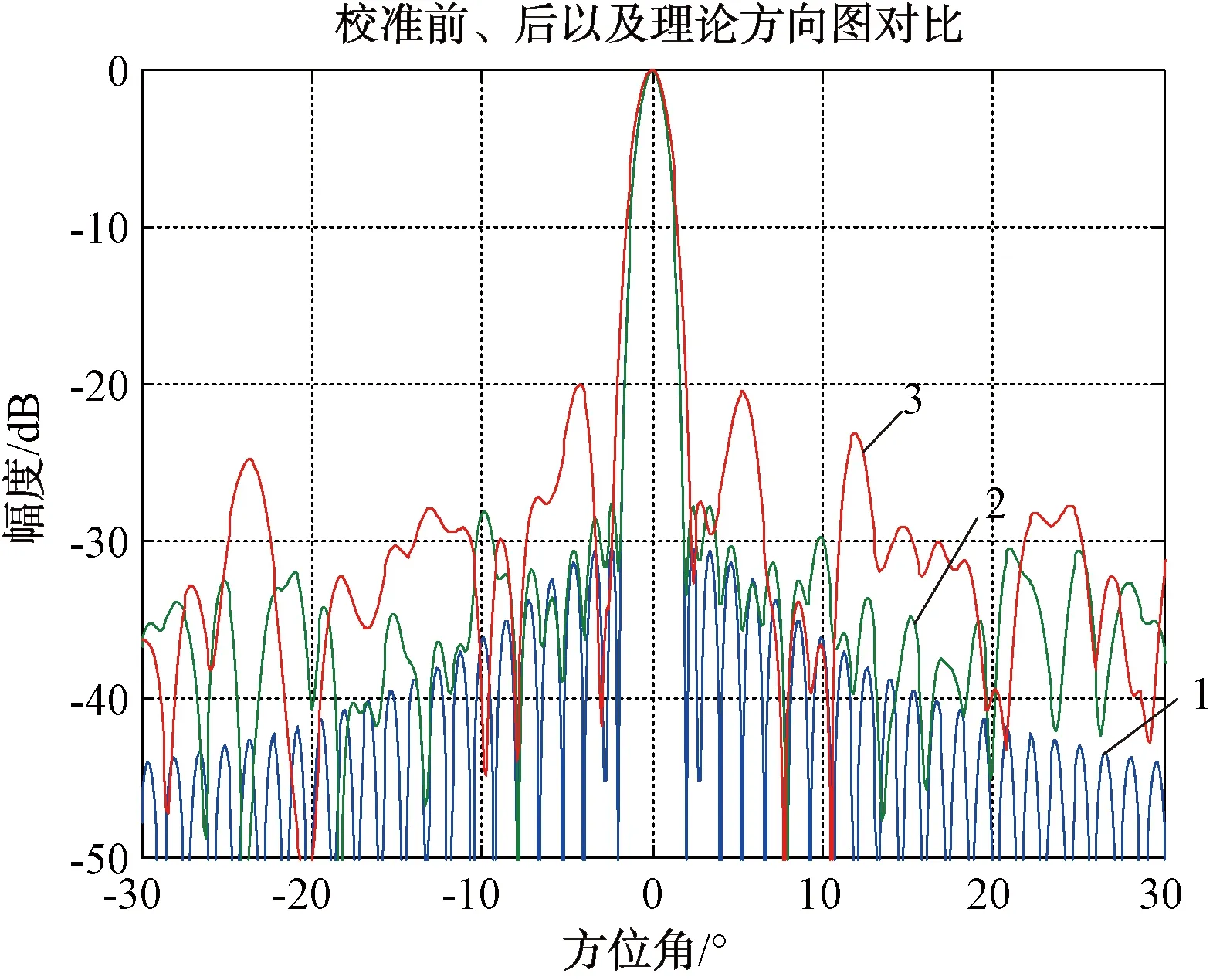
图6 阵列接收方向图
4 结束语
本文提出了一种应用于线性FMCW阵列雷达空间和时间校准的软件方法。该方法综合采用了时间域上的动态数字闭环校准法和空间域上的阵列展宽处理校准技术,通过对宽带X波段LFMCW雷达接收阵列系统的仿真与实验进行分析,证明该方法相对简单易行且有效。
