一种基于信息熵的加权混合预测模型

2021-06-16单曙兵张绍华

电子技术与软件工程 2021年5期

单曙兵张绍华

（1.中汇信息技术（上海）有限公司上海市 201203 2.上海计算机软件技术开发中心上海市 201112）

1 引言

在人工智能领域已经存在多种预测模型来解决不同的预测问题[1]。如传统的回归模型主要解决线性预测问题；而针对时间序列历史数据，可以采用自回归模型AR、移动平均模型MA 以及其他各种组合和变形的时间序列模型；神经网络模型和深度学习模型用于解决非线性预测问题等等。但单一的预测模型难以解决不同场景下复杂的预测问题，因而已经有诸多学者将两种或多种预测模型构成混合模型来取得更好的预测效果[2-4]。

张永峰等人将一维卷积神经网络模型与双向长短期记忆模型进行混合用于预测机器设备的剩余寿命，该模型不但可以有效地抽取时间序列上的特征，还可以产生更多的训练样本，从而提升预测精度[5]。王英伟等提出一种将ARIMA 和LSTM 混合的时间序列模型，实验结果表明该混合模型优于单一模型的预测[6]。郭海燕等提出了一种基于模拟退火算法优化BP 神经网络的预测模型，从而实现较好的负荷预测[7]。温海茹等提出将深度卷积神经网络和长短期记忆网络混合的预测模型，该方法在C-MAPSS 数据集上进行了验证，其结果优于单一的CNN 和LSTM 模型[8]。袁全等提出一种基于时间序列与天牛须搜索算法改进BP 神经网络的组合预测模型，仿真结果表明提出的混合预测模型好于单一模型[9]。黄伟建等提出将STAQI 模型和门循环单元模型进行混合，该模型用于预测空气质量其结果在均方根误差方面优于传统的深度学习模型[10]。上述模型都是通过一定的方法提升预测的精度，而如果在不同的预测阶段将预测精度最好的两个或多个模型进行混合，使其各自发挥解决不同预测问题的优势，实现更为精准的预测。因此本文提出一种由互信息和信息熵共同决定权重的加权混合预测模型。

本文所做的贡献如下：

（1）提出一种全新的由互信息和信息熵共同决定权重的加权混合预测模型，并命名为MPR；

（2）研究并讨论了如何选择待混合的模型，比较了经典的权重的确定方法优劣；

（3）通过真实的数据，并引入9 个基准模型从预测精度和方差比较了混合模型的优势。

2 加权混合预测模型

在本节中，我们将提出一个全新的混合模型MPR，它可以混合两种预测模型。公式（1）是MPR 模型的数学表达式，V 是预测值，w 是权重，A、B 表示预测模型。

在信息论中，熵可以量化信息源的信息不确定性[11]。在公式（1）中，模型A 和模型B 是信息源，而A 和B 作为信息源给出的信息实际上是预测准确度（例如1%，2%，...100%）。基于熵的定义，在我们的研究中，信息源的准确性越高，熵越小。但是，熵是对称的，也就是说，信息源的准确性差也导致熵的值小。为了解决这个问题，本文使用加权熵来降低精确度较低信息源的影响。并且，在本文的混合模型MPR 中涉及两个信息源，所以它们平均相互信息是相同的。因此,如果一个模型的平均相互信息与信息源的加权熵之比更大，则相应的信息源具有更准确的信息。在这个情况下，该信息源即预测模型在混合模型中的相关权重应该更大，也就是说混合模型整合了每个预测模型中更为准确和稳定的预测部分。

基于以上讨论，权重确定如下：我们首先使用训练数据集完成A 和B 模型的训练，然后将训练后的A 和B 模型分别使用验证数据集进行预测。这两个模型获得的结果的准确性是根据公式（2）计算的。在公式（2）中，aij是使用第j 个模型（即第j 个信息源）预测第i 个验证数据的准确性。Ri代表第i 个验证数据的实际值。Fij表示第j 个模型对第i 个验证数据预测值。

对于m 项验证数据，第j 个模型将产生m 个相应的精度值。如果使用列向量ATj=（a1j，a2j，...amj）T 表示第j 个模型的精度，则所有模型的精度值都可以用矩阵Amn 表示，如公式（3）所示。

表1：常见的9 个预测模型

图1：MPR 与9 个基准模型的预测结果对比

图2：MPR 模型与SGD 权重确定法预测结果对比

在矩阵Amn中计算每个精度值的出现次数（注意：精度值是实数，因此在计算精度值的出现次数时，我们仅考虑其整数部分（例如87%而不是87.15%）并得到等式（4）所示的Rmn，其中，rij代表第j 列中aij（其整数部分）的出现次数。

矩阵Rmn 中的每个元素将被代入到方程式（5），以分别获得A 模型和B 模型的加权信息熵。如上所述，加权熵为了使精度更高的信息源在混合模型中更加重要。我们可以计算方程（5）的加权熵。在式（5）中，Ej 是第j 个模型的加权信息熵（即，第j 个信息源）.wij'与pijlogpij对应，Nj 表示在矩阵Amn的第j 列中aij大于准确率X%的数量，其中X 依据实际需要取适当值。pij的第j 列中是rij的出现的概率，其中M 表示第j 列上rij的总和。

其中，

表3：MPR 与9 个基准模型的预测结果方差对比

表4：MPR 模型与SGD 权重确定法预测结果的差对比

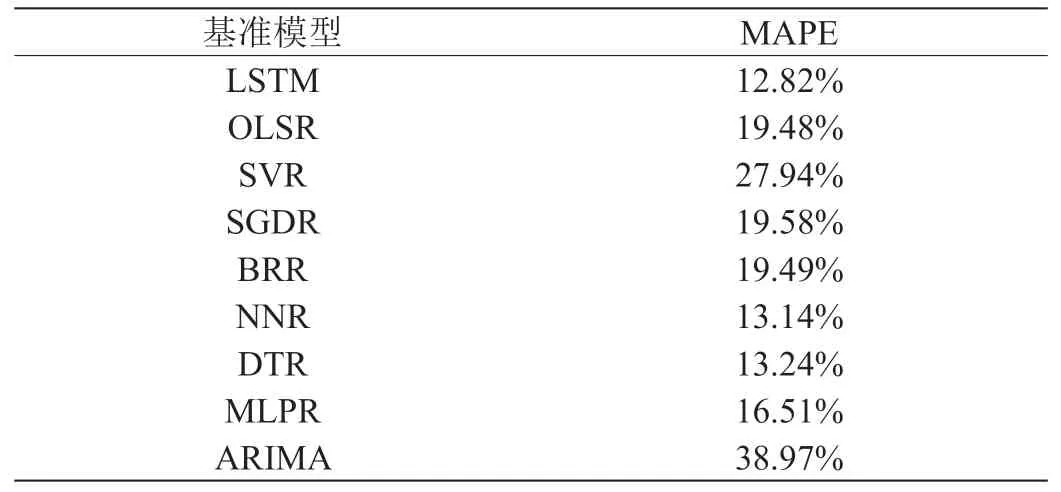
表2：9 个基准模型的预测结果

计算用于确定混合模型中权重的平均互信息的过程如下：如果ak=al，则定义阶跃函数UN(ak, al)=1，否则，UN(ak, al)=0，其中ak和al(k=l)是矩阵Amn 中的两行。定义ci = 1 + ∑mj,j≠iUN(ak, al)(1 ≤i ≤m）,可以得到向量CmT=（c1，c2，....cm）T。应用公式（6）获得两个信息源的平均互信息，其中J 和J’分别代表两个信息源。

其中，

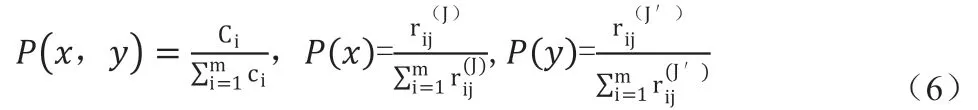
根据前文的讨论，MPR 模型中每个组成模型（即信息源）的权重是平均互信息与其熵的比值。第j 个信息源的权重将由等式（7）计算。在等式（7）中，I 是平均互信息，而Ej 表示第j 个源的加权熵，Z 是用于归一化所有基本算法的权重以确保所有权重之和为1 的参数。

3 实验结果

为了评估预测结果的质量，本文利用等式（8）所示的MAPE（平均绝对百分比误差）[12]，其中At 为实际值，Ft为预测值。

在计算实验中，我们采用9 种常用的预测模型（如表1 所示）作为基准。这些模型的某些应用可以在[13-14]中找到。它们代表7种不同类型的模型，包括广义线性回归，支持向量机，最近邻居，高斯过程，决策树，集成方法，神经网络，时间序列模型和长期短期记忆。

使用提出的MPR 模型和表1 的9 个模型预测平台访问流量，现已有1年的平台流量数据，并得知因素退出率、点击密度、平均会话时间影响平台的访问流量，并将上述数据划分为60%训练集，20%的验证集，20%的测试集进行实验。依据经验，公式（5）中的X 取70%，实验结果如表2 所示。从表2 中可以看出，LSTM模型和NNR 模型的预测精度位于前两位，选取这两种模型，并使用公式1 到公式7 计算提出的MPR 模型的预测结果，并与表2 中模型结果进行了对比，如图1 所示。从图1 中可以看出，提出的MPR 模型的预测的MAPE 值最小，其预测精度明显好于任何单一的基准模型。

此外，使用方差来评估所有模型的预测结果。表3 显示了MPR 与9 个基准的预测结果的方差。MPR 在方差方面表现最佳，这表明MPR 能够产生合理的结果。因而我们提出的MPR 混合预测模型整合了其组成部分的预测优势，不仅对精度有所提升，其稳定性也有较大提升。

4 分析与讨论

4.1 模型混合原则

在本文第2 节中MPR 模型混合了LSTM 和NNR，取得了良好的预测效果。但在进行模型混合时需要遵循两个原则，一是模型的多样性，二是预测表现。

4.1.1 多样性

多样性意味着混合的模型是不同的。因此，从统计学角度考察LSTM 和NNR 是否为不同的模型。为此，本文进行统计检验。由于通过算法获得的预测结果的分布是未知的，因此应使用非参数检验。类似于Ablanedo-Rosas[15]的研究，我们使用Wilcoxon ranksum检验（秩和检验）确定两个选择的样本是否具有相同的分布。在此，给出零假设：LSTM 和NNR 所获得的预测结果总体相同。使用开源scipy 软件用于通过调用stats.ranksums 进行测试，该测试的p 值为2.801e-106（<0.01）。因此，拒绝零假设，并确认LSTM 和NNR不是相似的模型。

4.1.2 预测性能

LSTM 和NNR 是实验中表现最优的两个模型，LSTM 是9 个基准模型中预测精度最高的，NNR 是9 个基准模型中方差最小的。而混合模型需要整合最佳性能模型。混合模型MPR 与9 个基准模型相比确实表现出最好的表现即精度最高并且方差最小。

4.2 不同权重方法的结果比较

某些优化算法，例如SGD（随机梯度下降等）通常用于确定模型的权重。但是，这种方法不但是黑盒，而且很容易陷入局部最优[16]。如果很难获得最佳权重，这会导致混合预测精度的折衷。本节使用SGD 算法确定方程（7）中的权重，并采用两个损失函数包括MSLE 和MSE（均方误差）分别实验。图2 中，SGD_mse 表示将具有MSE 损失函数的SGD 应用于确定权重的混合模型。SGD_msle 表示使用具有MSLE 损失函数的SGD 确定权重的混合模型。如表4 所示，平均方差也是最低的。