装配式桥梁横向分布分析及损伤识别

罗彦 蒋凌杰 毛建平

作者简介：

罗 彦（1971—），高级工程师，主要从事桥梁设计及检测工作;

蒋凌杰（1988—），工程师，硕士研究生，主要从事桥梁检测及监测研究工作;

毛建平（1985—），高级工程师，硕士研究生，主要从事桥梁设计、检测及监测研究工作。

文章阐述了横向分布系数在旧桥承载能力评定中应用的方法，分析了横向分布的影响因素敏感度，得到单片梁开裂和铰缝失效两种损伤的横向分布损伤识别模型，给出了基于荷载试验结果计算横向分布的公式，并进行了两座桥梁实测横向分布系数的计算及损伤识别分析，以验证梁损伤识别的有效性。

装配式桥梁;桥梁试验评定;横向分布;损伤识别

U448.21+8A461644

0 引言

装配式空心板梁桥在我国高速公路建设中应用广泛[1]。在近年的高速公路改扩建中，对该类桥梁的承载能力检测评定也越发受到重视。装配式桥梁荷载试验承载能力评定时，通常引入桥梁横向分布的概念，将空间计算化为平面计算，从而将桥梁空间计算转化为单梁模型计算。横向分布系数的准确计算是承载能力评定的基础，其准确性直接影响荷载试验效率、荷载试验理论值、荷载试验校验系数的准确性，从而影响桥梁承载能力评定结果。

1 横向分布计算基本原理及方法

横向分布计算将影响面函数分离成影响线函数进行求解[2]，从而达到化复杂的空间问题为简单的平面问题，如式（1）：

S=Pη（x，y）≈η（x）η（y）（1）

式中：η（x）——单梁截面的效应值影响线，即纵向影响线;

η（y）——梁的荷载横向影响线，即横向分布系数。

通過以上处理，即可以通过单梁模型求得某截面上的效应值η（x），再利用荷载分布系数η（y）计算梁的实际效应值。引入横向分布系数的方法，在同等精度条件下比空间分析的数值方法效率高。

杠杆法、刚接板梁法、铰接板梁法、修正偏压法和GM法是横向分布系数常用的计算方法，各计算方法的原理及适用范围不同。工程应用中，通常采用杠杆法计算支点的横向分布系数，采用其他方法计算跨中的横向分布系数。如装配式空心板桥采用铰接板梁法进行跨中横向分布系数的计算，该法通过刚度参数和板块的数量，确定梁板的荷载横向影响线 [3-4]，并根据荷载的横向分布计算横向分布系数。

2 横向分布影响因素分析

桥梁横向分布与桥梁的横向连接有关，与结构的影响线和荷载布置也有关，而影响线通过刚度参数及梁板数量求得。因此影响因素主要有：主梁截面刚度、梁板的数量、荷载横向位置以及横向连接刚度。

本文以铜鼓岩小桥荷载试验的计算过程为计算模型，分析横向分布系数随影响因素变化的规律。

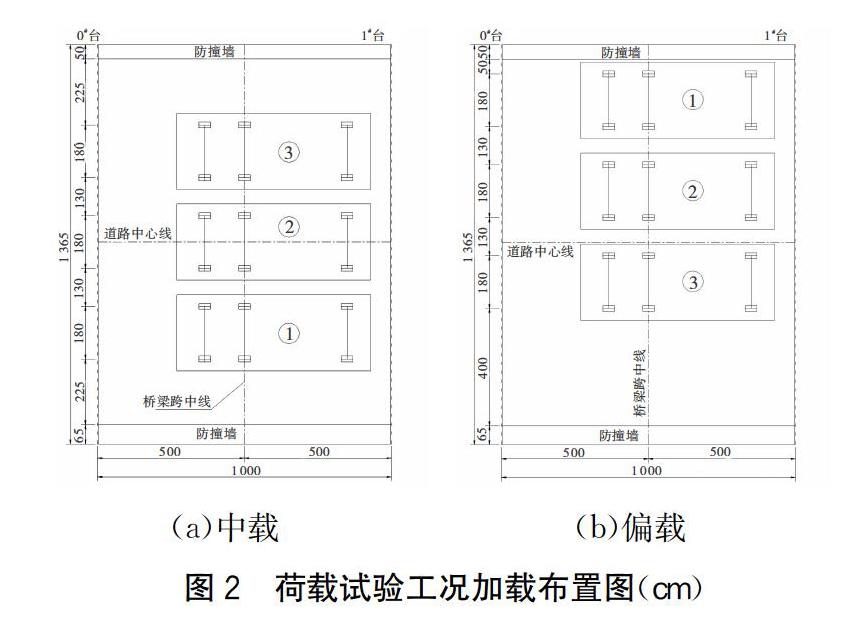
铜鼓岩小桥位于柳南改扩建工程K202+298处，桥梁全长17.52 m，其上构为1～10 m钢筋混凝土空心板，桥面按分离式双幅设置，单幅桥面宽13.65 m（0.5 m+12.5 m+0.65 m），设计荷载为汽-超20，挂车-120。桥梁断面图见图1。该桥为单跨简支梁桥，荷载试验以跨中断面为控制断面，分别进行中载和偏载工况，加载时采用单排横向3辆车布置，加载示意图见图2。

2.1 截面刚度对横向分布的影响分析

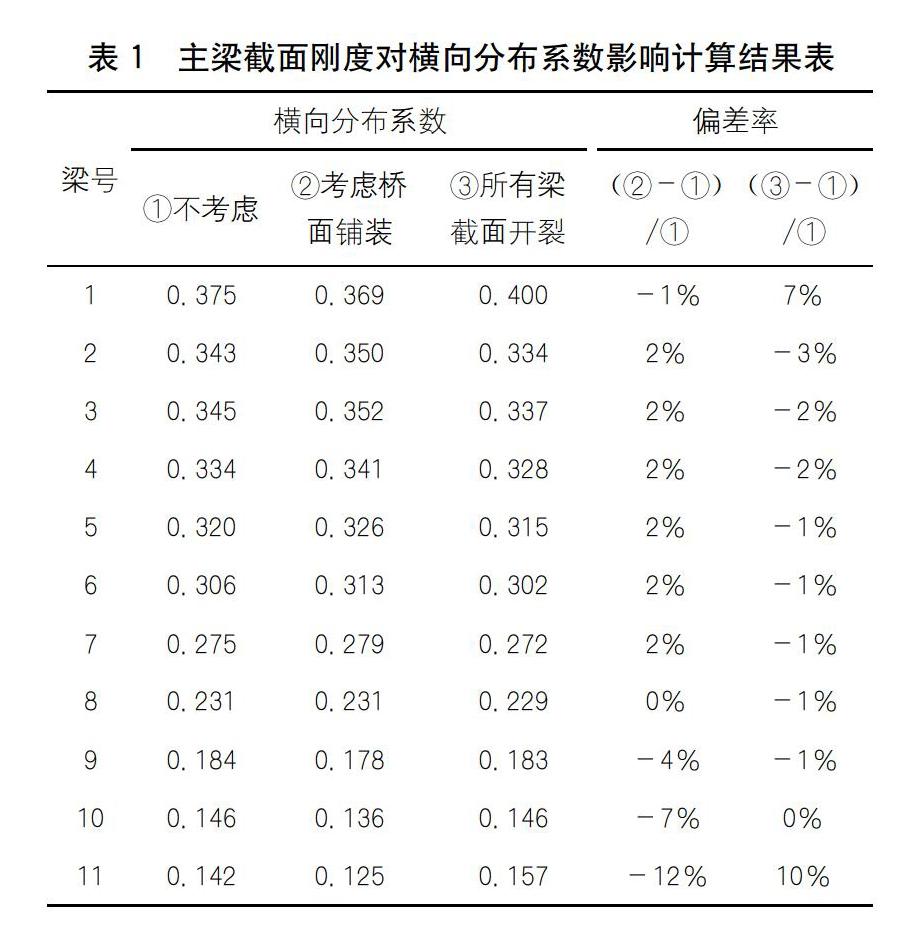
空心板的桥面铺装厚度相对空心板的高度较大，考虑桥面铺装明显提高主梁的整体刚度。中小跨径的普通钢筋混凝土空心板在荷载长期作用下出现较多的横向贯通裂缝，截面开裂也较大削弱截面的刚度。为研究其影响程度，采用桥梁博士3.0软件进行影响线的计算，以偏载工况横向布载为例，计算3种情况下的横向分布系数并对比分析，结果见表1。

由表1可知，在考虑桥面铺装整体刚度增加（约增大1倍）和考虑截面开裂整体刚度减小（约减小1倍）情况下横向分布系数基本保持不变，偏差率多数在5%以内，对荷载试验挠度及应变的计算值影响不大，但因为实际刚度直接影响实测的应变和挠度，最终导致实测试验挠度校验系数成倍的变化。因此，在进行荷载试验计算时，需计入桥面铺装参与荷载试验理论值的计算。

2.2 单板开裂对横向分布系数影响分析

以上分析了所有梁开裂的情况，而实际情况中每片梁的状况不一致，会出现单片梁开裂严重的现象。以铜鼓岩小桥中载为例，如5#梁开裂，按照开裂刚度重新进行横向分布系数计算，计算结果见表2及下页图3。

单片梁开裂后其承担荷载的能力减弱，横向分布系在该梁处数值变小，而两侧边梁的横向分布系数增大，且随着距离开裂梁的距离增加而增大。该横向分布规律可作为实测横向分布系数进行开裂识别的依据。

2.3 铰缝失效对横向分布的影响

近年来由于道路交通量的迅猛增加，造成梁板间横向传递部分失效情况越发明显，导致出现趋于单块板参与受力现象，影响结构的承载能力，威胁行车安全性 [5-6]。装配式空心板梁铰缝受力复杂，单从检测的表观缺陷难以直接判断铰缝是否存在内部损伤，因此，需分析铰缝内部损伤失效后对横向分布的影响。按照5#铰缝（5#梁和6#梁间铰缝）失效时重新计算跨中横向分布系数，结果见表3及图4。

由表3和图4可知，5#铰缝开裂后，5#梁处横向分布系数明显增大，且加载车辆多的一侧的横向分布系数也随着增大。其横向分布规律可作为荷载试验实测横向分布进行铰缝损伤判断的依据。

3 试验实测横向分布系数计算及损伤识别方法

横向分布系数可通过荷载试验实测挠度值进行计算分析得到。梁的横向分布系数值为各个主梁实测挠度值与各个主梁实测挠度值总和的比值，再乘以车道数来进行计算[7]，见式（2）。

mi=N·wi/∑ni=1wi（2）

式中：mi——试验荷载作用下第i片梁的横向分布系数;

wi——试验荷载作用在第i片梁的实测挠度值;

n——梁的数量;

N——加载横向车辆数。

根据理论分析，在采用实测值进行计算时，实测应变及实测挠度均可以用于横向分布系数计算，即wi可为试验荷载作用在第i片梁的实测效应值（应变值或者挠度值）。

以铜鼓岩小桥和龙凤二桥荷载试验实测数据为基础，采用上述方法计算横向分布系数，并进行损伤识别。铜鼓岩小桥横向分布系数计算见表4及图5。

由表4及图5可知，横向分布系数在5#梁处陡然增大，4#梁横向分布系数大于6#梁。根据前文损伤横向分布影响分析，可以判断该梁在5#和6#梁之间的铰缝内部存在损伤。

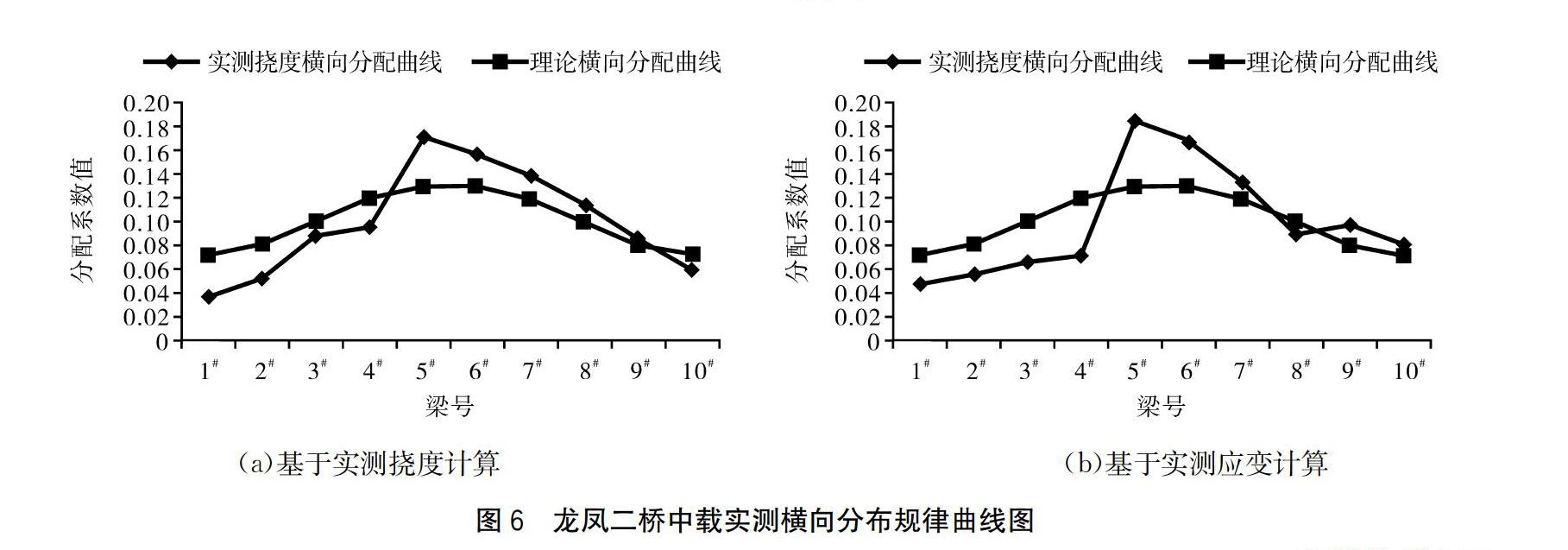
以同样方法计算了龙凤二桥的横向分布系数，得到横向分布规律（见图6）。由图6可知，中载工况下按照实测应变和实测挠度计算的横向分布基本一致，验证了前文分析的正确性。从横向分布规律可看出， 5#梁处横向分布系数陡然增大，6#梁的横向分布系数减小，根据前文分析结果，可以判断5#和6#梁之间的铰缝内部存在损伤。

结合两座桥的现场检测结果，损伤铰缝处存在有明显的开裂渗水，主梁的校验系数最大值接近1.0，且部分测点相对残余应变>20%，进一步判断铰缝基本失去传力性能，单板受力的趋势明显，急需进行维修加固。

4 结语

横向分布在桥梁检测评定中有着十分重要的作用，准确的计算分析是承载能力评定的基础。文章分析了横向分布影响因素及影响程度，明确了桥梁荷载试验时计入桥面铺装参与刚度计算的重要性，并得到了单梁开裂和铰缝失效下横向分布损伤识别模型。文中给出了基于实测应变和实测挠度进行横向分布系数分析的方法，以实际荷载试验项目为例进行了横向分布系数的计算，论证了实测应变和实测挠度进行横向分布系数计算的适用性，并结合实测横向分布系数规律和横向分布损伤识别模型，进行了桥梁损伤的识别，提出维修加固建议。本文为旧桥检测评定提供参考。

[1]范立礎.桥梁工程[M].北京：人民交通出版社，2006.

[2]姚玲森.桥梁工程（第二版）[M].北京：人民交通出版社，2008.

[3]雷晓红.荷载横向分布系数在混凝土桥梁加固检测中的研究[D].武汉：武汉理工大学，2006.

[4]韦立林，王文宁，王建军.简支梁桥荷载试验横向分布系数分析方法[J].广西大学学报（自然科学版），2007，32（2）：183-185，199.

[5]陈晓强，赵佳军，吴建平.板桥结构由铰缝引起的病害分析及加固改造[J].现代交通科技，2004（1）：46-48.

[6]王砚桐.高等级公路单板受力现象及原因分析[J].公路交通技术，2004（4）：29-32.

[7]李松辉，李 冲，闫 明.在役桥梁实测荷载横向分布系数研究与应用[J].山东科技大学学报（自然科学版），2009，28（5）：27-29，34.