在“画”中感悟概念

潘霞虹

摘 要：倍的概念是比较两个量之间的关系，对学生而言十分抽象、不易理解。为了让学生更好地认识倍并理解倍的概念，在教学中笔者试着對教材进行研读并通过调查对单元知识进行重新组合、编排、整合教学。“倍”的概念教学，教师应立足学生的认知起点，借助合理有效的教学手段——多元表征，让学生在自主学习、共同探究、求联求异中建构概念，使学生对“倍”的形成深度认知。

关键词：多元表征;“倍”的概念;深度学习

“倍的认识”是人教修订版教材三年级上册第五单元的内容，是小学数学中一个抽象而重要的概念。在学习“倍”之前，学生头脑中建构的关于比较两个数量大小的方法是比较数量的多与少，即比较两个数量的差，也就是常说的差比。在比较两个数量关系时，除了差比，还可以将一个量确定为标准量，通过判断另一个量里面有多少个这样的标准量，来比较两者的比率关系，也就是倍比。比率这一概念在数学学习中有着重要的作用，是学生学习比例的基础。实际上，倍、表示分率的分数、百分数、比等概念的本质都是比率，而“倍的认识”是学生第一次接触比率，之后的小数倍、分数（表示分率）、百分数、比的内容，都可以看作是对“整数倍”的扩展。“倍的认识”的地位和作用也就不言而喻了。

一、课前调研，了解学情

为了了解学生是否知道“倍”，他们了解的“倍”是否是数学中所教学的“倍”，笔者对所任教班级进行了前测。通过前测可以发现，学生对“倍”的认知并不是零起点，有相当一部分的学生并不陌生，在进一步交流访谈后，学生对“倍”又似懂非懂，无法用“谁是多少，谁是多少，谁就是谁的几倍”这样的句式来表达。并且在表征“倍”时，受实际生活的影响，学生对“多几倍”和“几倍”概念上较为混淆。可见，学生对“倍”的本质理解有较大的偏差。

二、解读教材，掌握意图

小学生的数学认知结构主要是加法结构和乘法结构。理解两个数量的倍数关系是学生乘法认知结构建立的重要方面，而“倍”是加法认知结构到乘法认知结构的转折点，是乘法认知结构的起始阶段。如何在学生现有的知识经验基础上，改变原有的认知，优化“倍”的教学？笔者从对比教材入手，分析比较，试图掌握教材背后的编写意图。

（一）不同版本的编排对比

笔者主要以人教修订版、苏教版与浙教版教材进行对比。

人教修订版以“小兔子数萝卜”为情境，通过数一数、圈一圈，把2根胡萝卜看作1份，红萝卜就有这样的3份，红萝卜的根数里有3个2根，就说红萝卜的根数是胡萝卜的3倍。这里有两个特点：一是重观察、重操作，以直观的方式让学生加深“倍”的理解;二是通过旧知识“几个几”和新知识“倍”建立对接，帮助学生理解倍的内涵。

苏教版以“小朋友数花”为情境，通过问题“你能比一比这三种花的朵数吗”展开教学。教材先出现学生之前已经学过的“比多少”，接着通过圈一圈，用“倍比”的方法得出黄花是蓝花的3倍。在这里，它主要强调的是“倍”是由两个数量相比较而产生的，并且是在学生已经熟悉的差比关系基础上引发新的生长点。

浙教版教材以“游艺室里挂气球”为情境，把2个红气球看作1份，蓝气球有这样的3份，就说蓝气球的个数是红气球的3倍。接着通过挂气球的个数变化来呈现“标准量”、“比较量”和“倍数”之间变与不变的关系。它则更凸显对“倍”概念的辨析和理解。

（二）人教版的实验版与修订版教材对比

教学时段不同：在人教版的实验版教材中，“倍”的认识被分散安排在二年级上册和下册，从乘法的角度引出倍的含义。而在修订版教材中，则集中安排在三年级上册的第五单元。一方面，整体后移，降低了学生的学习难度;另一方面，集中教学“倍”，学生不受乘除法的限制，更利于加深对“倍”内涵的理解，教学更富有逻辑性与结构性。

主题图使用不同：这里主要是有两处明显不同。一是使用的事物不一样，实验版用的是小棒，修订版用的是小兔和萝卜，显然，后者的情境更能激发学生的学习兴趣。二是呈现的方式不一样，实验版采用的是活动方式类的，而修订版使用的是自然情境类的。从操作变为观察，弱化了对图形的关注，进而转变为对关系的关注，从而更好地突出“倍”的本质：是两个量比较的结果。同时，用“圈一圈”代替摆，更重视图画表征，强调通过图形直观，经历把“2个胡萝卜看成一份，6个红萝卜就有这样的3份，红萝卜根数就是胡萝卜根数的3倍”的认识过程，亲身经历倍的形成过程，同时也渗透了画图策略，为后面解决“一个数是另一个数的几倍”奠定基础。

三、多元表征，深度学习

笔者根据各版本教材的特点以及实际的学情，重新设计教学方案：以“画”为媒，以“比”为线，以“用”为根，以此促进学生的深度学习，真正建构起“倍”的概念。

（一）以“画”为媒，思维可视化

借助“数学魔盒”这样一个有趣而神秘的情境，让学生通过观看，直观认识学生最熟悉且最简单地“2倍”，之后将实物情境图演变为象形示意图，形成标准的“2倍”直观模型，建立2个几和2倍之间的联系，并且把学生模糊的、直觉的“倍”进行数学化的规范——形的规范、语言表达的规范。

之后学生开始两次的“画图”表征——在“初画”中理解2倍，在“再画”中强化几倍，将自己的思维通过表征变得外显、可视。

【教学片段1】

师：小朋友，如果你面前也有这样的一个数学魔盒，你想放进去几个笑脸，出来会是怎么样的？把你的想法快速地画在学习单的第一题上。

——学生动手画一画：

师：谁愿意来介绍一下自己的作品？

生1：把进去的4个笑脸看作1份，出来的笑脸有这样的2份，出来的笑脸是进去笑脸的2倍。

如果说刚才的实物魔盒只是让学生直观认识2倍，那么这里就是帮助学生加深对2倍的理解。通过让每一位学生现场画一画，将自己对2倍的理解内化、表征出来，丰富了2倍的图示，同时，以形辅数，一步步帮助学生从具体的量抽象乘集合图，不断深化2倍的意义，建立2倍的直观图式。

【教学片段2】

师：刚才，我们主要认识研究了2倍，想一想，生活中是不是只有2倍呢？现在请你想一個自己最喜欢的倍，然后把它画在学习单的第二题中。

第一小题是已知进去的圆的个数，画出来的个数，是顺向思维;第二小题是已知出来的圆的个数，画进去的个数，是逆向思维。这里再一次借助“画图”，从笑脸到圆形，再次内化“几倍”的概念本质。同时学生的建模经验进行初步类推，实现了从具象到抽象，从2倍到多倍的转化，并为后面进一步深入理解倍提供学习素材。

（二）以“比”为线，知识结构化

概念教学要关注概念的实际背景以及概念形成的思维过程。抽象的数学概念的形成可以借助有形的数学活动，通过活动铺就概念与学生思维的通道，帮助学生有效建立概念。学生掌握概念的过程也是一个不断发展的过程，往往经历建立概念表象、抽象概念本质、厘清概念结构、辨析概念间关系这几个阶段。而在本堂课中，笔者以“比”为主线，层层深入，帮助学生建立“倍”的概念。

1. 建立概念表象

概念的表象是指对概念具有鲜明形象的感知，将头脑中的概念经过外部信息进行转化，是对概念进行知识表征的过程。虽然学生在学习之前，对“倍”有初步的感知，但他们无法用语言表述什么是“倍”。所以笔者创设了“数学魔盒”的情境，通过具体的实物表征“倍”的含义，通过3次对比，尝试说一说数学魔盒的秘密，以此来激发学生对“倍”的语言表征，促使学生在头脑中建立“倍”的表象。

2. 抽象概念本质

概念是事物本质属性的反映。它的形成一定是一个从具体到抽象的思维过程。如果说数学魔盒中认识的“2倍”是一个表象，那么学生初画2倍后的对比，就是抽象“2倍”本质的一个过程。通过“为什么这里都可以说出来的笑脸个数是进去的2倍”这一问题的设计，让学生在不同作品的求同中完善“2倍”的概念及图式。同时，通过“再增加2个笑脸，会有什么变化”和“如果要使出来的笑脸个数是进去的4倍，该怎么办”，让学生从不同的角度建构倍的图示模型，挖掘“倍”的本质，理解“一个数里有几个几”就是“一个数是另一个数的几倍”，明确“倍”隐藏着“包含”关系，以此达到对“倍”本质的理解。

3. 厘清概念结构

“倍”概念非常抽象，而小学生思维又是具象的，所以教学时要将概念与实例相结合，借助实例教学概念，从而厘清概念的知识结构。

在“再画”几倍后，学生的反馈主要分为三类：第一类是第一小题，也就是一份数相同，但倍数不同;第二类是第二小题一份数不同，倍数也可以不同;第三类是特殊的倍：一份数是1个和1倍的情况。在交流的基础上，然后通过两次对比和追问——“在这里，进去的都是2个圆，为什么倍数关系却不相同？”和“现在出来的都是6个圆，怎么它们的倍数关系还在变化呢？”感悟标准量、比较量和倍数之间变与不变的关系，加深学生对标准量1份数的理解，加深几个几和倍之间的联系，帮助学生厘清“倍”的结构关系。

4. 辨析概念间关系

通过对比和辨析，可以加深学生对概念的正确理解与建构。在小结中，沟通了倍比和差比的新旧知识联系，帮助学生梳理知识，明确概念，形成网络。

借助“比”，将学生的画图表征、语言表征、概念理解、数理表述都有机地结合起来，让学生看着自己的图来说理，降低了数理表述的难度，数学的“多元表征”让原本“高冷”的数理瞬间变得亲切，自然，也让学生对倍本质的理解变得更加直观。

（三）以“用”为根，策略模型化

画是为了最终的“不画”，数学的学习最终要走向生活应用。这里通过3道精心设计的练习题，让学生层层深入，直击“倍”的本质。

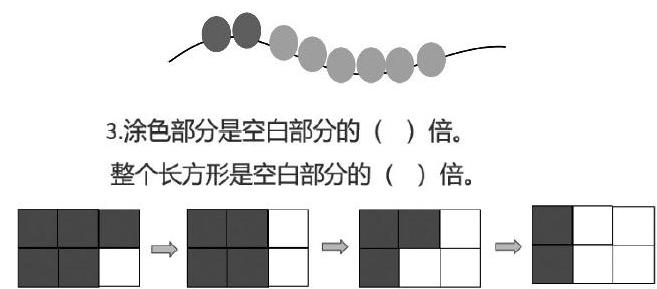
练习一从整齐排列到杂乱无章，打破之前建立的倍的直观模型，迫使他们去关注倍的本质——几个几，实现了从图到数的转变。练习二通过解决“蓝珠子是红珠子的（ ）倍”这样一个问题，从一串手链到2串、3串手链，把一道题用透、用深，让学生初步感知两个量都成倍增加时，它们之间的倍数关系是保持不变的。练习三是长方形色块的涂色问题。一方面，从之前的实物抽象到图形，更为重要的是之前所接触的倍都是两个物体之间的比较，这里是部分与整体的比较。同时还让学生直观感知了除整数倍外，还有小数倍、分数倍，把倍的内涵从整数扩展到分数，打通了与后续知识的联系。另一方面，通过“形”直观体验变化的规律，感受一个数据随着另一个数据的变化而变化的过程，初步体验函数思想。

曹培英老师对学生几何直观能力培养分为三个层次：一是直观感知水平能力，二是直观理解水平能力，三是直观深化水平能力。笔者的本堂课，虽是“倍”概念的起始课，但也遵循曹老师的三个层次，数学魔盒的识2倍，是第一层次，是个体理解，属于特殊情况;之后的2倍的集合模型和多倍认识，属于一般化情况，是第二层次;在串珠、长方形色块涂色中，属于系统化情况，是第三层次。总的来说，笔者借助“画”，通过“比”，回归“用”，既符合学生的认知思维，又促使他们对“倍”进行了深入探究，让“倍”在学生的头脑中深度发生。

（浙江省宁波市镇海蛟川双语小学，宁波 315000）