一种单相双模式高效双Buck 逆变器的研究
2021-06-14胡志杰
胡志杰,傅 强
(青岛大学电气工程学院,山东青岛 266071)
当今世界,人类各方面的发展步入了高速阶段,能源供应是人类发展至关重要的基础[1]。传统化石能源储量有限,不能满足人类社会可持续发展对能源的需求量,新型可再生能源的开发利用成为当务之急[2]。太阳能是新能源中的典型代表,太阳能发电是太阳能应用的主流途径,其技术发展比较成熟[3]。光伏逆变器是太阳能发电装置中的核心环节,它的性能影响着整个系统的安全性、可靠性[4]。
光伏电池板能量输出极其不稳定,其输出电压、电流变换范围较宽。在光伏逆变器的发展初期,较为实用的单级全桥逆变器属于Buck 型变换器,其输出电压较低。为提高其输出电压,将Boost 直流升压变换器与全桥逆变器进行级联,产生了常规的两级式升压逆变器,这能够解决输出电压过低的问题。但这种逆变器的功率开关工作在高频状态,直流输入侧与输出侧的地端之间存在高频共模电压,而光伏电池板本身存在对地寄生电容,因此会形成漏电流[5],降低了系统的效率和安全性。目前,比较有效的解决方案包括加入隔离变压器、在直流侧增加一个或者两个功率开关管,形成H5和H6桥逆变器。但是加入隔离变压器会降低系统发电效率,增大逆变器体积和成本。H5和H6桥逆变器只能降压逆变,会导致电压不足,于是产生了将Boost 变换器与H5、H6 桥级联的两级式逆变器,既有效抑制了漏电流,又提高了逆变器的输入电压,但这种方案电路内的开关管均工作在高频状态,使系统的开关损耗增加[6-7]。
文中研究了一种无变压器且能有效抑制漏电流的双模式双Buck 逆变拓扑。该拓扑结构既能实现升压逆变功能,又能降低开关管的工作频率,从而减小损耗,提高系统效率,并且不存在漏电流问题,可应用于光伏、风电新生能源发电系统。
1 拓扑结构和工作过程分析
1.1 拓扑结构
所研究的无漏电流的高效双模式双Buck 逆变电路拓扑结构如图1 所示。

图1 双模式双Buck逆变电路拓扑
该逆变拓扑采用两级式结构,前级为DC-DC Boost 变换电路,后级为全桥双Buck 逆变电路,输出滤波采用LCL 滤波器[8]。该电路拓扑具有两种工作状态:1)前级不工作,通过旁路二极管D1为后级逆变电路直接供电;2)两级均工作,此时前级升压,开关管S0工作在高频状态,后级全桥双Buck 电路相当于周波变换器,开关管工作在工频状态[9-10]。
1.2 工作原理
所提出的无漏电流高效双Buck 逆变拓扑实现了直流升压与逆变功能。在一个开关周期内,共有8种开关状态。图2所示为一个开关周期内的开关时序。

图2 系统一周期内开关时序
以下对于两级全桥双Buck 逆变拓扑的分析均建立在理想情况下,电感工作在电流断续(DCM)模式。
系统正负半周期各有4 种开关状态,两组Buck单元分别在正负半周期内为负载供电,前级视输入电压大小改变,负半周期与正半周期开关状态类似,不再赘述。图3 所示为正半周期的电路开关状态。
开关状态1:如图3(a)所示,S1、SP导通,S0、S2、SN截止,光伏电池板直接向逆变器供电,同时为电容C2充电。逆变器工作在正半周期,S1处于高频开关,SP半周期常开,稳态时满足以下关系:

开关状态2:如图3(b)所示,SP开通,S0、S1、S2、SN截止,逆变器通过D3续流,电感L2电流下降,稳态时满足以下关系:
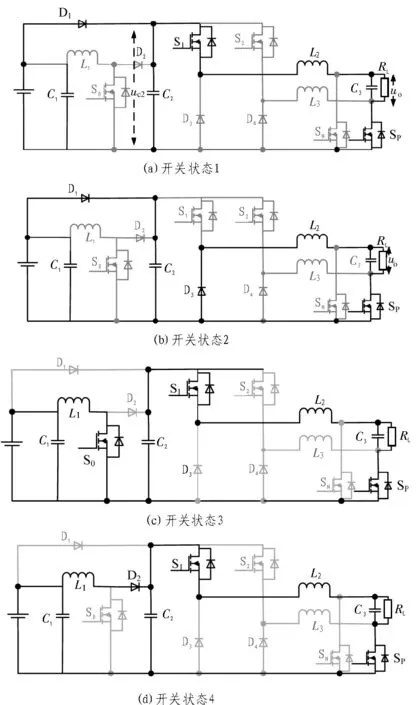
图3 电路的开关状态

开关状态3:如图3(c)所示,S0、S1、SP导通,S2、SN截止,在此状态下,前级Boost 的升压电感充电,后级逆变电路由电容C2正向供电,稳态时满足以下关系:

开关状态4:如图3(d)所示,此时S1、SP导通,S0、S2、SN截止,光伏阵列经Boost 变换器向全桥双Buck逆变器供电,电容C2充电。S1、SP以50 Hz 的频率开通关断,稳态时满足以下关系:

通过一个周期内的各个模态方程,加之对应的模态时间,利用伏秒平衡原理可求得逆变器在单周期的状态平均值,通过单周期内的平均值和状态平均值可得到电压增益公式,如下:

其中,m为调制比,f为开关频率。
所以该两级式拓扑既能实现升压逆变功能,又不会产生对地漏电流,而且两种工作模式的转换减少了开关管的开关次数,使整个系统更加高效可靠。
2 控制策略与补偿网络设计准则
文中对所提逆变拓扑使用单极性SPWM 调制技术对开关管进行驱动[11-12]。单周期内,开关管S0在光伏电池供电电压不足时处于高频开关状态,即前级升压电路工作,而光伏电池本身电压足够时,S0处于常关状态;S1和S2工作状态互补,分别对应于工频周期的正半周和负半周。前级工作时,两开关分别在各自的半周期内常开;前级不工作时,两开关分别在各自的半周期内高频工作;SP与SN在一周期内互补导通。采用电压外环与电流内环闭环控制[13-14]输出电压。控制框图如图4 所示,其中补偿部分采用PID补偿,图5 所示为PID 补偿算法电路图。
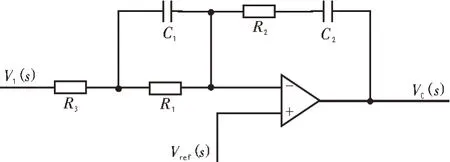
图5 PID补偿算法电路图

图4 系统整体控制框图
PID 补偿的函数为:

由上述公式可得闭环补偿存在两个极点,分别为:

由上述公式可得闭环补偿存在两个零点,分别为:

设置开关频率为40 kHz,PID 补偿后的截至频率为开关频率的0.1 倍,期望相位裕度设为45°,期望幅值裕度设为10 dB,最大超前角为67°,可得:
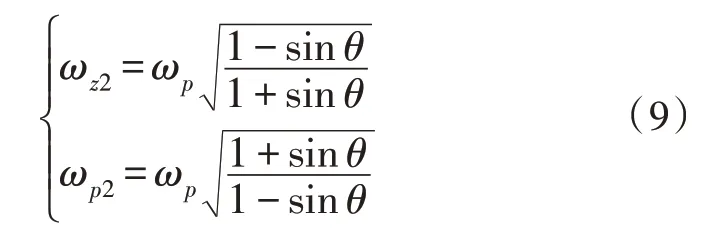
将PID 补偿中积分补偿角速度设为100 rad/s,可得PID 补偿函数如下:

其中,K为增益补偿。
设图5 中R2=10 kΩ,可由式(6)和式(10)求得其他参数。
3 仿真验证
文中搭建了基于PSIM 仿真软件的双模式单相双Buck 电路模型[15-16]。仿真各项参数如下:输入电压100 V,输出电压AC220V,输入滤波电容100 μF,升压电感30 μH,直流母线电容100 μF,输出滤波电感1 mH,输出滤波电容30 μF,负载为纯阻性负载。各开关管驱动波形如图6 所示,S0仅在需要升压时高频工作,S1、SP与S2、SN正负半周互补工作,在不需要升压时高频工作。仿真输出电压电流波形如图7 所示,输出电压总谐波畸变率约为4%。直流母线电压波形如图8 所示。
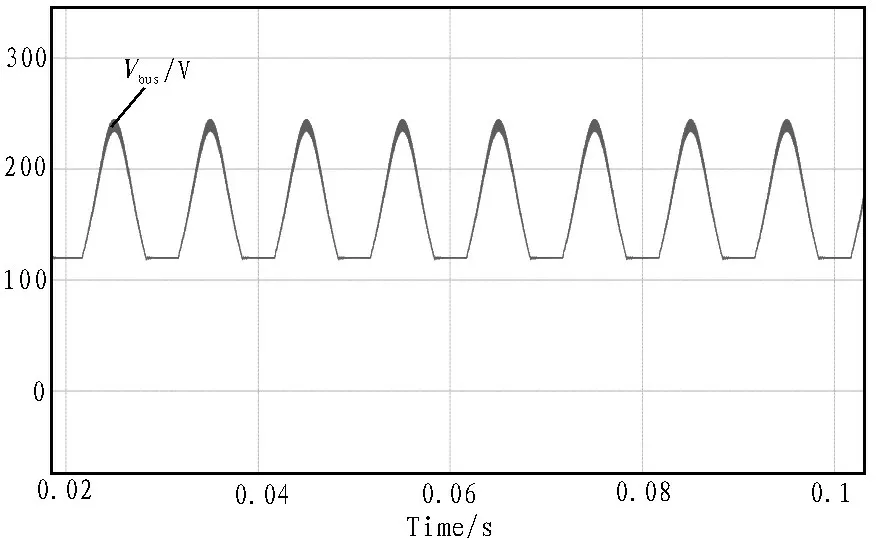
图8 直流母线电压波形

图6 开关管驱动波形

图7 输出电压电流波形
4 结论
文中将双模式控制策略应用于小功率单相并网逆变器,并研究分析了电路的工作原理及电路元件的参数,通过仿真验证了控制方案的正确性,得到了满足要求的输出波形,验证了逆变拓扑的可行性,同时满足了光伏并网逆变器对升压和逆变的要求。
