基于滑动窗口的LSTM地温预测方法
2021-06-14马尚昌
唐 旺, 马尚昌, 李 程
(1.成都信息工程大学 电子工程学院,成都 610025; 2.成都理工大学 地球科学学院,成都 610059)
近几十年随着工业的发展,由于自然释放或人类活动排放,导致全球气候以变暖为特征[1]。在全球变暖的大背景下,人们关注气温变化的同时,也在关注地温的变化[2]。地温即土壤温度,能直接影响土壤微生物的活动和作物的生长发育[3],它对植物种子的萌发、生长发育、根系活动和产量等有极大的影响[4]。全球地表平均温度在过去100年中增加了0.78℃。同时,在近50年里,中国的年平均地表温度升高了1.1℃,增温速率为0.022℃/a[5]。R.K.George[6]指出,对于土壤温度、气温、风速、相对湿度、降雨量等的预测对于农业是有用的,所有这些气象参数都与农业生产高度相关;除了对农业领域的影响以外,下垫面能量交换过程对大气环流、天气变化、人类生存环境和可持续发展同样具有重要影响[7];刘均荣等[8]通过在高温环境下对不同类型岩石的实验研究,分析了岩石渗透率在高温作用下发生变化的机理;盆地现今地温场特征与油气田分布具有良好的对应关系,可为今后油气勘探提供地热学依据[9];地热变异是沉积盆地形成和演化的动力学原因,也是沉积盆地中地球化学动力学过程和物理化学过程的重要因素:因此,地温场的参数对盆地动态模拟和油气地质研究尤为重要[10]。综上,对地温的研究存在重要的意义,即提前预知未来的地温高低和变化趋势,能给农业、大气科学、地质学等领域的研究提供帮助。
全国平均地温的年代际变化大致经历了3个阶段,即地温下降阶段、相对气候冷期和20世纪90年代后期的升温阶段[11]。Tang等人[12]利用线性回归和BP神经网络对成都市地温进行预测,发现BP神经网络预测效果优于线性回归,且模型对冬季预测效果较差,春夏秋3个季节预测效果较好;杨孟达[13]改进PSO-LSTM神经网络对气温进行预测,相比于BP、RNN和LSTM模型,此方法具有更高的预测精度;杨耘等人[14]利用BP-LSTM对新疆天山山脉中段玛纳斯河流域及其周边地区进行气温预测,结果显示BP-LSTM比LSTM的均方根误差(RMSE)小2.21℃,比LSTM与多元线性回归组合模型的均方根误差(RMSE)小0.3℃;此外,BP-LSTM的平均绝对误差(MAE)也比其余2种模型更小。
目前使用人工智能的方法在气象领域尤其是气温和降雨方面已有大量研究,并且都取得了较好的实验结果,而对于地温的预测研究还相对较少。且当前传统的长短时记忆神经网络(LSTM)方法对长时间序列的预测可能存在较大误差,而滑动窗口法(SW)可以根据时间推移周期性地更新数据集,从而可将长时间序列划分为周期性的短时间序列。结合LSTM和SW解决长时间序列预测时误差较大的问题。
1 数据和方法
1.1 数据
1.1.1 数据来源
本实验地温数据来自于四川省成都市温江气象站近50年(1968—2017年)的日平均地温数据,共计18 250条数据(为方便计算,不区分闰年和平年,即总数据为50年×365天/年)。数据分为2个子集:训练集和测试集。训练数据集为1968—2007年记录的共14 600个数据,占总数据记录的80%;测试数据集包含3 650条数据记录,占总数据的20%。
1.1.2 数据初步分析
通过对数据的初步分析,从图1中可以看出成都市的年平均地温在近50年内,呈现了先上升、后下降、再上升的大致变化趋势,并且总体呈现小幅度的上升趋势,满足之前学者的研究结论。进一步地,从图2中可以看出地温高低具有明显的季节性差异,春季和秋季的平均地温非常接近,平均值大约在15~22℃,夏季平均地温超过25℃,冬季平均地温低于10℃。由于输入LSTM模型训练的数据序列若存在较大波动,可能会对神经网络的训练造成影响甚至降低精确度,因此为了确保模型的精确性与科学性,本研究将训练5个模型,分别预测全年日均地温、春季日均地温、夏季日均地温、秋季日均地温、冬季日均地温
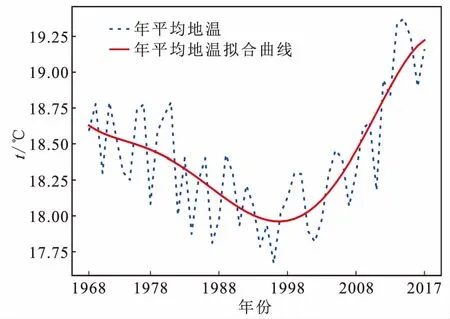
图1 成都市近50年的年平均地温Fig.1 The annual average ground temperature in Chengdu in resent 50 years

图2 成都市近50年四季平均地温Fig.2 The average seasonal ground temperature in Chengdu in recent 50 years
。
1.2 方法
1.2.1 相关系数
相关系数是用以反映变量之间相关关系密切程度的统计指标。为了确定当日平均地温是否与前几日平均地温存在一定关系,本研究采用相关系数的方式来判定,地温的数据集合可用矩阵表示
X= (X-n, …,X-1,X0)
(1)
其中:若假定X0表示当日平均地温;则X-1表示昨日(过去第1日)平均地温,X-n表示过去第n日平均地温。以当日平均地温和昨日平均地温计算为例,相关系数计算的公式可表示为
(2)
其中:cov(X0,X-1)为X0和X-1的协方差;var(X0)和var(X-1)分别为X0和X-1的方差。
1.2.2 长短时记忆神经网络
循环神经网络(RNN)可以预测具有时间序列的数据;但时间序列过长时,会导致模型对训练数据的遗忘,即时间梯度消失。由此引入长短时记忆神经网络(LSTM),解决此问题。本实验中,采用LSTM模型预测未来短期内几天的日均地温,LSTM模型的输入数据必须转换为规定的三维矩阵,可用以下公式表示
Xn→(xsamples,xtime_step,xfeatures)
(3)
其中:Xn为时间序列样本;xsamples为每次输入数据的个数;xtime_step为时间步长,其数值代表用前多少天的数据来预测;xfeatures为预测的特征标签,其数值代表有几种预测的参数类型。
1.2.3 滑动窗口法
传统的LSTM预测方法,主要分为2种。第一种是利用前n个数据预测未来1个数据,即使用时间序列Xn预测Xn+1可用以下公式描述
Xn= (X-n, …,X-1,X0)
(4)
Xn→LSTM→Xn+1
(5)
其中:Xn为当前1个数据与前n个数据的集合;Xn+1为未来的1个数据。由于预测完成后Xn保持不变,输入数据仍为(X-n, …,X-1,X0),所以此模型只能预测未来1个固定不变的数据。
另一种是利用前n个数据预测未来m个数据,可用以下公式描述
Xm=(X1,X2, …,Xm)
(6)
Xn→LSTM→Xm
(7)
为了使LSTM能够有效地预测未来多个数据,本研究在模型中加入了滑动窗口法(SW),让Xn能够随时间进行更新。引入SW更新数据后,预测未来t日数据,可用以下公式描述
Xpre= (Xpre,1,Xpre,2, …,Xpre,t)
(8)
Xn+pre= (X-n+t, …,X0,Xpre)
(9)
Xn+pre→LSTM→Xpre,t+1
(10)
其中Xpre为未来t个预测结果的集合。公式(9)代表更新后的序列,公式(10)代表采用更新后的序列进行预测。此方法有效解决了上述预测值恒定的问题。但此方法仍存在弊端:预测较长的时间序列时,输入集全部更新为预测值,误差将持续累计向后传递,整体预测误差也将不断上升。若时间序列越短、间隔越小时,那么滑动窗口方法的预测精度则会越高。
考虑到上述问题,本研究进一步采用周期性SW,即每隔一段时间将测试集的预测值重新替换为真实值,其原理是将长时间序列拆分为多个短时间序列,从而解决误差累计传递的问题。可用以下公式描述周期更新参数的方法
XTi,act=(XTi,-n,…,XTi,-1,XTi,0)
(11)
XTi,act→LSTM→XTi,prej
(12)
TTi,act+prej=(XTi,-n+k,…,XTi,0,
XTi,pre1,…,XTi,prek)
(13)
其中XTi,act为周期i的真实值矩阵。公式(12)代表对周期i的预测,XTi,prej为周期i中的第j个预测结果。若假设已有k个预测值,公式(13)为周期i中的参数更新方法。周期性更新参数的方法需要通过实验找到误差突变的时间点,将误差突增时刻之前作为一个周期,从而确定周期的时间长度。
1.2.4 基于滑动窗口的LSTM模型
滑动窗口(SW)的主要功能是更新参数,解决LSTM对长时间序列预测可能存在较大误差的问题。此方法主要用于测试集的输入更新阶段,即模型的预测阶段,应用此方法时未改变模型的训练过程。若以时间步长等于3为例,模型的预测过程可用图3表示。

图3 周期性SW+LSTM预测的过程Fig.3 The process of periodic SW+LSTM prediction
图3中,输入部分,数字1、2、3代表真实数据;输出部分,字母P代表预测数据。在每一个周期内,解决了传统LSTM仅能预测单个值或固定的多个值,不能随时间推移向后预测的短时预测问题;在多个周期的结合后,解决了随时间推移误差累计传递的长时间序列预测问题。图3中仅展示了一个周期的数据更新和预测流程,每个周期的方法均相同。在实验过程中,周期的具体数值需根据预测的误差突变时刻来确定。
纸盒后传来哧哧的轻笑,纸盒移开,露出一张年轻女孩的脸,是四小姐。刘雁衡看到她两颊上各有一抹潮红,心里说:“哎,膏粱子弟,吃饱了撑的。”
1.2.5 数据归一化
使用数据归一化将输入数据转换为0到1之间的数字,这有2个优点:一方面,梯度下降时它可以收敛得更快;另一方面,它可以提高结果的准确性。在本研究中,使用最小-最大归一化方法来处理数据。归一化函数用以下公式描述
(14)
其中:Xscale是归一化后的数据;X代表日平均地温;Xmin为日平均地温的最小值;Xmax为日平均地温的最大值。部分日平均地温的归一化结果见表1。
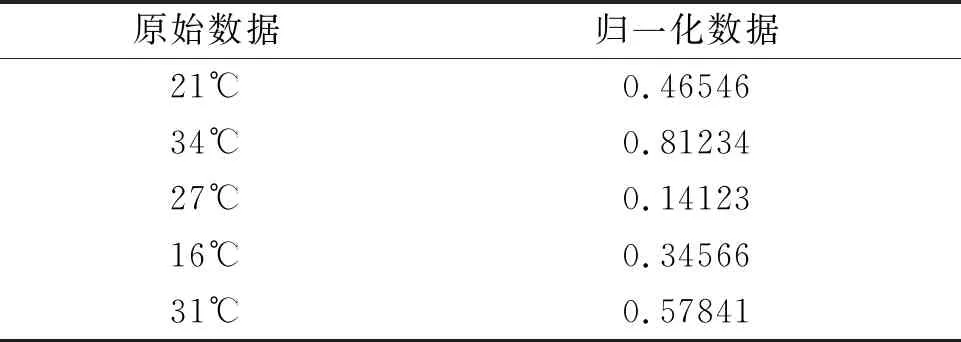
表1 部分日平均地温归一化结果Table 1 Part of normalized results of daily average ground temperature
1.2.6 预测精度评价
本实验采用均方根误差(RMSE)和平均绝对误差(MAE)作为模型预测的评价标准,计算方法可用以下公式描述
(15)
(16)

2 结 果
2.1 相关系数结果
通过计算当日平均地温和前几日平均地温的相关系数,从数量上确定了两者之间的相关程度。如表2所示,从全年数据来看,前7日与当日的平均地温呈现极强的相关性,但程度在逐渐降低。从图4中可以看出,四季平均地温也大致满足全年的相关性规律,但其中夏季的相关性较弱。总的来说,随着时间推移当日平均地温与前几日平均地温的相关性逐渐降低。进一步,需通过实验确定LSTM中的时间步长。

表2 全年当日与前7日平均地温相关系数Table 2 Correlation coefficient of annual average ground temperature between the same day and the previous seven days in a whole year

图4 四季当日与前7日平均地温相关系数 Fig.4 Correlation coefficient of annual average ground temperature between the same day and the previous seven days in four seasons
2.2 时间步长实验结果
经过不同的时间步长实验,图5和图6展示了全年和四季的模型训练效果,分别是它们的平均绝对误差(MAE)和均方根误差(RMSE)。从两个图中均可以看出,误差与时间步长近似成正比关系。理论上使用步长为1的误差最小,但考虑到实际的预测,仅仅用前一天预测后一天,这种方法的预测结果可能存在偶然性;而步长为3时,5个模型的MAE和RMSE大致接近于步长为1的结果:因此,后续研究将采用步长为3的模型进一步预测分析。

图5 平均绝对误差与时间步长关系Fig.5 Mean absolute error and time step
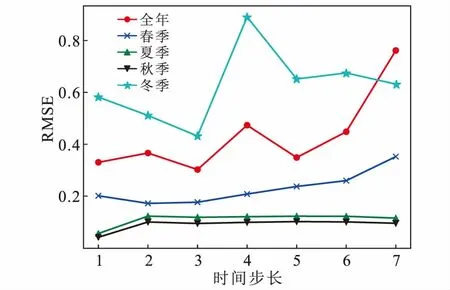
图6 均方根误差与时间步长关系Fig.6 Root mean square error and time step
2.3 模型预测结果
根据滑动窗口法,不断地更新输入数据集,通过实验证明了:随着输入样本的不断更新,在一定时间范围内地温的预测效果良好,但随着时间的增加,预测误差将不断上升,结果如图7,输入前3天的日平均地温,对未来14天的日平均地温进行预测,结果显示预测4日内的地温效果良好,从第5日开始误差快速上升。因此,本研究将采用前3天的日平均地温预测未来4天的日平均地温,即以7天为一个周期,按此方式循环,对2008—2017年的数据进行预测分析。表3展示了5个模型的预测平均误差:冬季模型整体预测效果最佳,近10年的平均误差小于1℃;春季和秋季模型平均误差约为1℃;而夏季模型预测效果较差,平均误差超过2℃。由此看来,全年模型受到夏季预测不佳的影响,整体平均误差也接近于2℃。
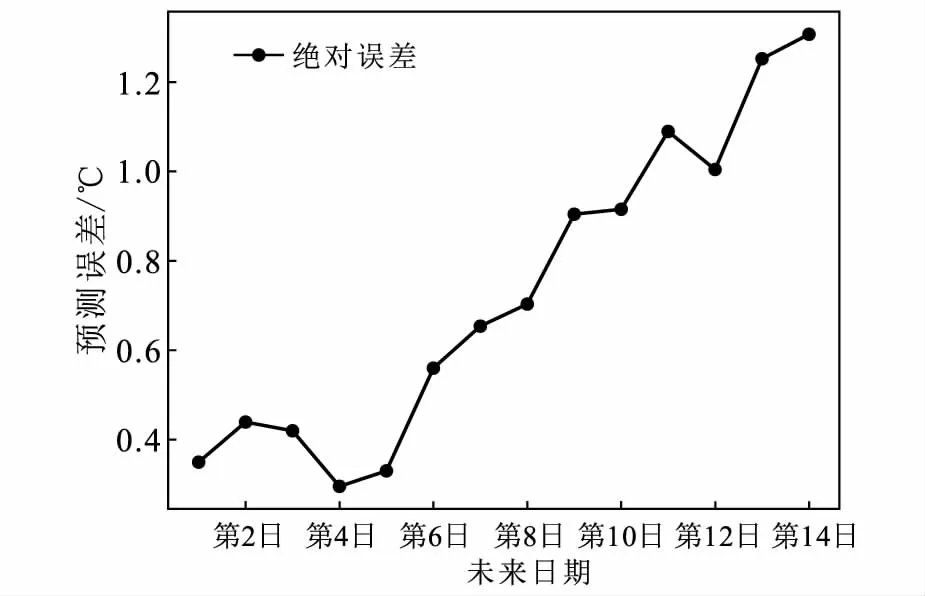
图7 预测未来的天数与误差关系Fig.7 The relationship between predicted future days and error

表3 2008—2017年各模型地温预测误差情况Table 3 Ground temperature prediction error of each model from 2008 to 2017
进一步以2017年的结果为例,图8中展示了用全年数据训练的模型对2017年地温的预测情况,整体平均误差约为1.7699℃。可以看出模型对于春秋冬的预测结果明显优于夏季,印证了上述相关系数的结论,即夏季当日的日均地温对前几日的日均地温依赖性较弱。图9至图12分别展示了春夏秋冬4个模型对2017年四季的预测结果。其中冬季预测结果最佳,平均误差约为0.7674℃;春季和秋季的预测结果接近,误差均为1.1℃左右;而夏季误差则达到了1.7979℃。此外,还可以明显地看出,春秋冬的预测数据曲线和真实数据曲线重合度极高,具有相同的递增或递减变化趋势。而夏季由于每日温度波动较大,没有明确的递增或递减趋势,存在较大温差,模型无法对此情形做出有效的预测。
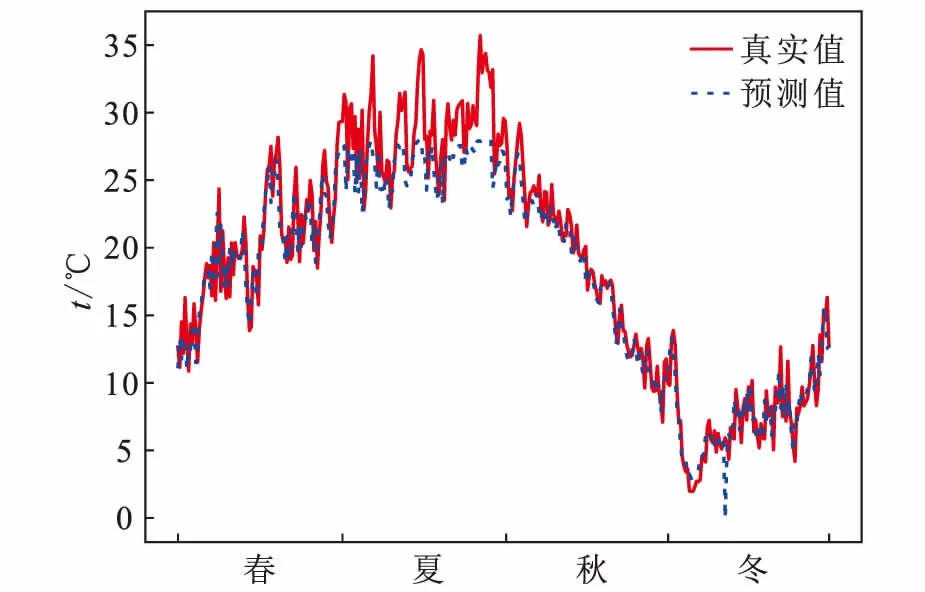
图8 2017年全年地温预测结果Fig.8 The results of ground temperature prediction in 2017
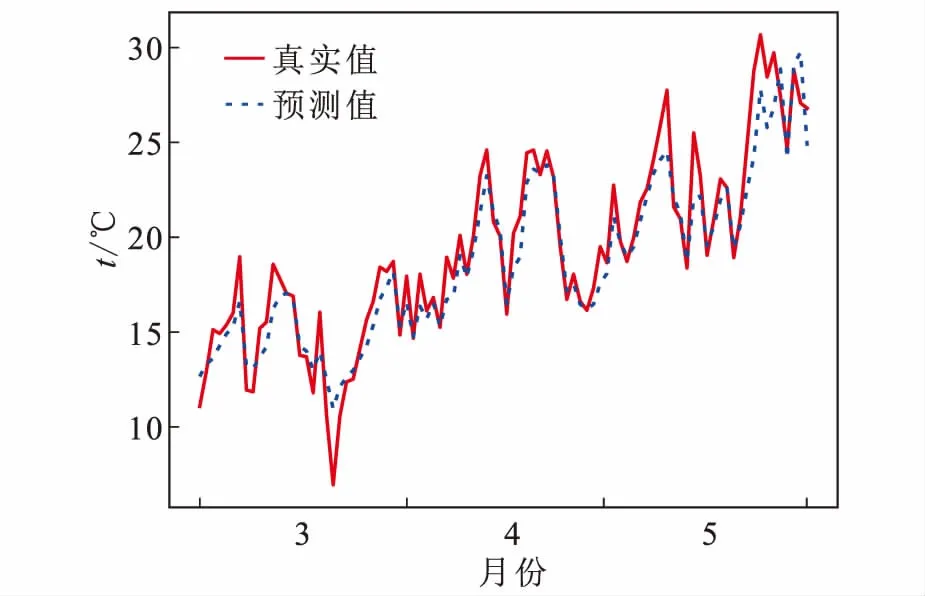
图9 2017年春季地温预测结果Fig.9 The results of spring ground temperature prediction in 2017

图10 2017年夏季地温预测结果Fig.10 The results of summer ground temperature prediction in 2017

图11 2017年秋季地温预测结果Fig.11 The results of autumn ground temperature prediction in 2017

图12 2017年冬季地温预测结果Fig.12 The results of winter ground temperature prediction in 2017
2.4 模型预测对比实验
传统的LSTM有2种预测情况,一种为单个值的预测,另一种为多个值的预测;而周期性SW+LSTM方法显然是多个值的预测。本实验针对多值预测的结果,对本方法和传统LSTM、BP-LSTM的预测结果进行比较,详细结果见表4和表5。其中,周期性SW+LSTM的2项指标均为最小,预测效果最佳;其次是BP-LSTM;最差是传统LSTM。
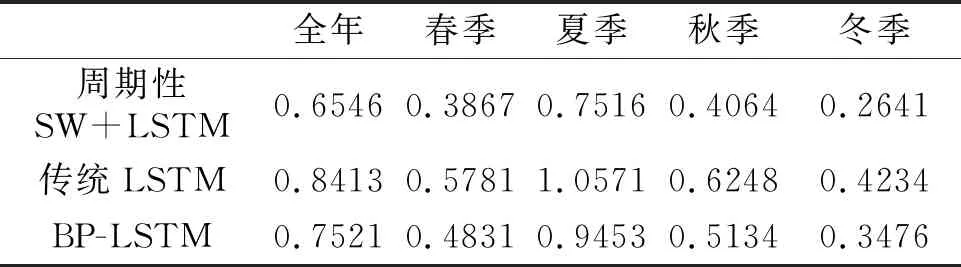
表4 周期性SW+LSTM与传统LSTM预测结果的 平均绝对误差Table 4 MAE of periodic SW+LSTM and LSTM prediction
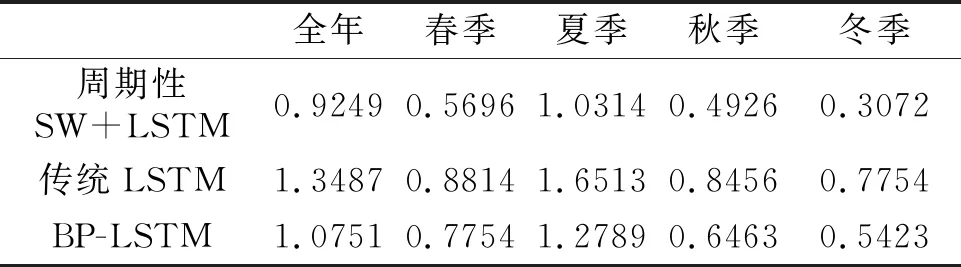
表5 周期性SW+LSTM与传统LSTM预测结果 的均方根误差Table 5 RMSE of periodic SW+LSTM and LSTM prediction
3 结 论
本研究采用传统长短时记忆神经网络(LSTM)结合滑动窗口(SW)的方法,以7天为周期更新参数,对成都市温江气象站1968—2017年近50年的地温进行分析计算,获得良好效果,得到如下结论:
a. 2008—2017年平均全年模型的MAE约为0.6546℃。进一步地,四季模型中,冬季模型预测效果最佳,MAE约为0.2641℃;春秋两季模型的MAE较为接近,分别为0.3867℃和0.4064℃;夏季模型的MAE略高,约为0.7516℃。
b. LSTM+SW方法能够很好地预测短时间内未来几日的地温,但随着预测天数增加,误差也会逐渐增大。通过周期性SW+LSTM的方法,将长时间序列拆分为周期性的短序列,降低了预测误差。
c.经过对比试验,周期性SW+LSTM的平均绝对误差和均方根误差均为最小,预测效果最佳;其次是BP-LSTM;最差是传统LSTM。说明此方法能够在一定程度上减小LSTM预测误差。
d.当日平均地温与前几日平均地温呈现较强正相关关系,但在夏季此关系较为薄弱。且预测结果与相关性具有紧密的联系,即相关性越高的参数输入模型,能够降低模型训练的平均绝对误差和均方根误差。
e. LSTM模型对于有明显递增或递减趋势的时间序列,训练和预测效果更好;而对于无变化趋势,时间序列上前后数据波动较大的情况,该模型则不能很好地训练和预测。
