公交疏散高危疏散单元集识别模型研究

李孟晖，杨益鸣

(中国港湾工程有限责任公司，北京 100027)

0 引 言

在区域应急疏散组织中，除对私家车疏散的组织外，对公交车疏散的组织也是应急疏散中十分重要的一部分。在卡特里娜飓风灾难过后的十几年来，公共交通疏散的相关问题在世界范围内已有较为广泛的研究。但是当前疏散模型大都忽略了不同集合点的差异性，具体体现在不同集合点的疏散需求以及可用疏散时间存在差异性，另外，由于资源的有限性，需要最大化利用可用资源，故需建立公交资源的分配原则。本文以此为切入点，提出疏散风险的概念，采用“风险优先”的分配原则，量化疏散风险，建立高危疏散单元集识别模型，用于识别当前疏散风险最高的一系列集合点，并以此确定各集合点公交派遣的优先级。体现不同集合点之间的差异性，帮助应急管理部门更合理的安排有限疏散资源。

1 疏散风险参数确定及表达

疏散区的路网结构可以抽象成有向图G(N，A)的网络拓扑结构，其中N和A分别代表网络中的节点集合和连接节点的弧集合，其中N由两类节点组成：N=P+S，其中P代表着一系列预先设定好的集合点，表示为{P1，…，Pn}；S代表着一系列终点，表示为{S1，…，Sm}。

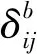
对于公交疏散而言，疏散风险主要由灾难动态、需求以及供给状态等参数确定，一次需要对以上参数进行合理度量。对于灾难动态的参数化，论文采用灾难影响到达前的可用疏散时间(H)来解释灾难动态对集合点的影响，某一集合点的可用疏散时间表示为Hi，可以通过已有预测模型获得。总时间窗口为T，可用疏散时间描述了与灾难相关的疏散风险影响因素。

对于需求水平和资源供给状况对疏散风险的影响，采用疏散完成时间(E)这一参数来表示。疏散完成时间即从疏散开始至最后一名疏散者离开危险区之间的时间间隔。某一集合点的疏散完成时间表示为Ei，表示为

(1)

其中di为初始时刻集合点Pi剩余的人数，表示为

(2)

由于当期可用疏散时间和疏散完成时间都是从时间这一角度对疏散风险进行的统一单位度量，因此而这可以通过直接运算将灾难特性、供给以及需求三者的动态有机结合在一起。

论文对疏散风险的定义为：在当前供应条件下，位于某一集合点的所有疏散者是否能够安全完成疏散。若能，则富余时间有多少，若不能，则会有多少疏散者最终被困在原地。因此，可用疏散时间与疏散风险呈负相关关系，而疏散完成时间与疏散风险呈正相关关系，集合点Pi的疏散风险risk(Γ)可以表示为

riski=-(Hi-Ei) ∀i∈P

(3)

该表达式通过在当前公交分配方案下疏散完成的富余时间的相反数作为量化疏散风险的标准。需要注意的是由于疏散完成时间Ri的表达式为非线性结构，因此会大大提高模型计算的复杂度，因此，在不改变风险表达式中两部分的相对大小关系的前提下，将其做一个转换来变成线性结构，如下

(4)

Ri表示集合点Pi的疏散风险。

2 高危疏散单元集识别模型

通过对高危疏散单元的识别，确定在不同的公交资源供给状态、不同灾难特性以及不同是需求水平下公交资源初始分配。用B0表示初始可用公交总数量，要求B0满足B，其中n为疏散区域内集合点的数量，即可用的公交数量必须大于集合点的数量来保证每一个集合点都至少有一辆公交车进行服务，否则该集合点将失去存在的意义，完全可以从集合P中剔除。在满足该前提条件下，将剩余可用的公交资源根据当前的疏散风险进行合理分配。

模型的决策变量有

δi：二进制变量，如果集合点Pi被选入高危疏散单元集，则δi=1，否则δi=0。

构建模型

Min.R∀i∈P

(5)

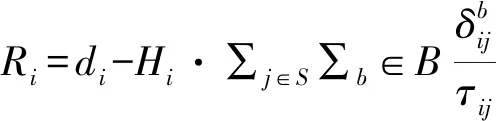
s.t.

R|Ri∀i∈P

(6)

(7)

(8)

(9)

(10)

(11)

(12)

δi∈{0，1} ∀i∈P

(13)

(14)

模型的目标函数表示最小化R。而在接下来的约束中令R的值不小于集合点疏散风险的最大值。式(6)要求R大于等于疏散区内任意集合点的疏散风险，然后通过目标函数表达式(5)来最小化R，即最小化疏散区内集合点疏散风险的最大值。上述模型可以通过识别一系列疏散风险最高的集合点来对有限公交资源的分配，进而完成DEU的确定。该模型的目标可解释为从集合点点集{Pi}中选择疏散风险最高的一个或几个集合点，并通过加派公交来降低其疏散风险，该过程可以认为是一个迭代过程，即不断地将公交从可用公交集合B中派往疏散风险最高的集合点，根据风险计算公式得到更新后的疏散风险，直到该集合点的疏散风险不是最高，在对当前疏散风险最高的集合点重复此过程直至将所有可用巴士派遣完毕。为了更好地理解，可以将各集合点置入平面直角坐标系中，x轴坐标为集合点编号i，y轴坐标为其对应的疏散风险值，将各点连接起来可得到一个折线图，而该模型做的就是“削平”波峰，即将波峰的高度降至最低。式(7)表示每辆车在初始阶段最多被派遣一次，即在同一时间不能被同时派往两个集合点。式(8)表示派往集合点的所有车辆数不得超过总量B0。式(9)表示每个集合点至少有一辆公交车服务。式(10)说明公交服务人数不得超过总需求量。式(11)和式(12)共同表示若有除最低限制的一辆公交车外还有其他公交车派向集合点Pi，则Pi被选入高危疏散单元集。

3 数值算例

上述模型将通过简单网络进行求解及验证。每段黑体路段的通行时间定为5 min，各集合点的初始疏散需求、初始当期可用疏散时间、公交往返时间均在表1中给出，根据上节模型可以计算出不同供给条件下的公交分配方案。

表1 各集合点初始属性及不同资源供给状态下的公交分配方案

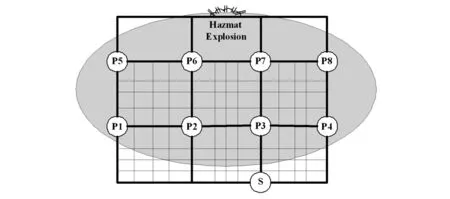
图1 无预警事故发生的简化网络及集合点位置分布

由表1可以看出，在初始阶段，当路网中存在32辆公交车时，灾难影响范围内所有集合点的疏散人群均可以在灾难影响到达前完成疏散。其中深色及浅色区块所对应的集合点为高危疏散单元集，例如，当可用公交的初始值为B0=17时，高危疏散单元集包括{P2，P6，P7，P8}，而当B0=10时，高危疏散单元集={P6，P7}。另外深色区块代表在起始时刻新增车辆的派遣方向。例如，当B0从10提升到11时，新增的一辆公交将被派往P6。论文中的高危疏散单元集模型为静态资源分配模型，旨在以了解高危疏散单元集的确定机制以及通过此模型确定在规划阶段确定所需的公交数。在实际疏散行动中，由于可用公交资源总量的变化、灾难传播的变化，以及随之改变的各疏散点的需求水平变化，公交资源的分配会随时间而呈现动态变化，而这一切都是由以上要素共同确定的各疏散点的疏散风险决定的。

4 结 语

本文提出疏散风险的概念，反映了公交疏散中不同集合点的疏散需求以及可用疏散时间存在差异性，通过灾难动态、需求以及供给状态等参数对疏散风险进行表达，以此作为判断不同集合点救援车辆派遣优先级的原则，进而建立高危疏散单元集识别模型，帮助应急管理部门更合理的安排有限疏散资源，并具有较高的实际应用价值。