基于IALM的穿墙雷达成像算法

张珊珊，赵建华

西安工业大学 电子信息工程学院，西安710021

穿墙雷达成像（Though-the-Wall Radar Imaging，TWRI）是一种利用低频电磁波的穿透性对复杂场景或障碍物后隐藏目标进行有效探测、定位和成像的技术，在应急救援、医疗监护、城市安保和反恐斗争等领域都发挥着巨大作用[1]。

穿墙成像中常采用超宽带（Ultra Wide Band，UWB）信号作为发射信号来提高距离向分辨率和探测精度[2]，但传统基于香农-奈奎斯特采样定理（Shannon/Nyquist Sampling Theory）的成像算法均存在着采样率高、数据量大、数据传输、存储及后续数据快速处理较为困难等不足[3]。此外，雷达成像近似视为对探测场景进行的最小二乘估计，使得基于匹配滤波思想的传统成像算法会出现较高旁瓣，使得成像结果模糊，无法区分邻近目标，成像质量不高[4]。

近年来，国内外学者通过研究与压缩感知（Compressive Sensing，CS）理论结合的雷达成像算法，以此来改善传统算法的不足。美国Rice大学的学者Baraniuk在研究雷达成像时引入CS理论，并在后续的仿真模拟中，利用正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法成功重建成像场景，验证了压缩感知雷达成像的可行性，这也是研究者第一次通过理论证明了压缩感知成像算法优于其他传统成像算法[5]。美国的Gurbuz第一次通过仿真模拟实验验证了压缩感知技术在探地雷达成像的可行性，利用地下目标空间的稀疏性，运用压缩感知思想，从有限次观测数据中重构出原始目标像，验证了该方法相比于传统BP方法在成像质量、鲁棒性和测量带宽要求上更有优势[6]。我国的余慧敏等学者则侧重于压缩感知雷达三维成像领域的研究，结合高斯脉冲体制的探地雷达，采用稀疏约束的正则化算法对随机孔径位置压缩测量的回波数据进行恢复[7]。2010年，压缩感知技术被Huang等人应用到穿墙雷达成像中[8]，提出了利用压缩感知算法随机采样返回到各个天线位置的所有回波数据，再通过重构算法获得图像。维拉诺瓦大学的Yoon等在研究穿墙雷达成像时提出了随机选择若干个天线位置上相同的频率，再采样进行压缩感知，重建各个天线位置的数据信息，最后进行各个部分的拼接成像[9]。

基于CS理论的雷达成像系统可采用低速的A/D转换器进行采样，极大程度地降低了雷达接收端对采样速率的要求，简化了硬件设计，同时基于CS理论的成像算法通过引入稀疏的正则化约束，直接建立成像场景与测量数据之间的线性关系，使得基于CS理论的成像算法往往成像效果更好，但在重构过程中须严格遵循非线性的稀疏约束，对信噪比要求较高，计算过程较复杂，且在TWRI实际应用中，墙体反射回波能量远远大于目标回波能量，导致目标信号常被杂波信号所覆盖，这使得目标的检测变得十分困难。因此，设计一种同时兼顾抑制墙杂波和目标成像的算法显得尤为重要。

本文针对传统CS成像技术对噪声敏感、计算过程复杂的问题，提出一种CS框架下的基于非精确增广拉格朗日乘子（Inexact Augmented Lagrange Multiplier，IALM）的穿墙成像算法。将TWRI问题视为正则化最小二乘优化问题，利用成像场景的稀疏性，分析回波信号数据矩阵，引入IALM进行迭代求解，先建立步进频穿墙雷达信号模型，构造目标回波信号稀疏表示字典；再利用随机测量矩阵实现降采样，最后将目标成像和墙杂波抑制视为一个含核范数和l1范数的复合优化问题，减少迭代次数，保证成像实时性。

1 基于非精确增广拉格朗日乘子的穿墙雷达成像

1.1 CS基本原理

设x是一个长度为N、稀疏度为K的离散信号，则x可用一组基ΨT线性组合表示：

其中，α为x在Ψ上的稀疏系数矩阵，Ψ为x的稀疏变换基或字典矩阵。

构造一个合适的采样矩阵，将高维信号x投影到低维空间上进行降维采样，则通过降维采样矩阵Φ=[φ1,φ2,…,φm,…,φM]后的采样信号可表示为：

其中，y是采样后的M×1维的观测信号，Φ是M×N维的测量矩阵，x是N×1维的离散型原始信号矩阵，M为采样的维度，M≪N。则可推出：

其中，A是M×N维传感矩阵或感知矩阵。重构准确性和稳定性决定于A是否满足约束等容特性（Restricted Isomety Property，RIP）[10]条件。

信号重构可通过对式（3）求逆运算得系数α，再恢复原始信号x。由于Φ的列数远大于行数，使得未知数个数远大于求解方程个数，求解式（3）等同于求l0范数约束的优化问题，解的个数不唯一。若放宽约束条件，将非凸的l0范数松弛为凸的l1范数，即转化为具有唯一解的凸优化问题[11]：

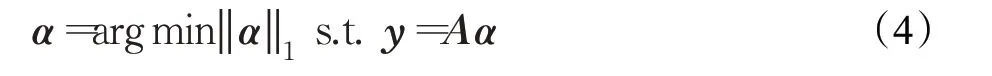
其中，‖‖1表示l1范数。

1.2 信号字典矩阵的构造

系统利用合成孔径技术（SAR）的思想，利用单站雷达的运动产生与目标之间的相对位移，把小的实天线孔径合成为一个等效的大虚拟孔径，提高方位向分辨率。如图1所示为穿墙雷达系统探测示意图。

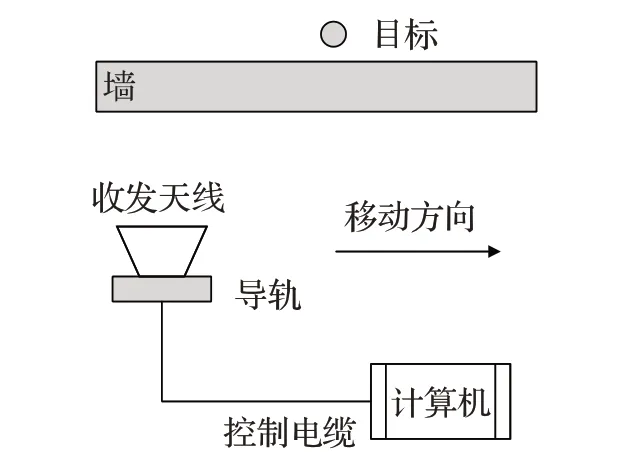
图1 穿墙雷达系统探测示意图

依据探测模型，雷达系统采用的是超宽带步进频信号体制，设采样测量点有M个，且每个测量点会发射N个频率步进的雷达脉冲，则第n(n=0,1,2,…,N-1)个发射信号频率为：

其中，f0为初始频率，Δf为频率步进量。

天线沿平行于墙面的水平界面上匀速移动，则第m(m=0,1,2,…,M-1)个位置第n个频点的目标回波可表示为：

其中，P表示探测区域内散射目总数，σp表示目标点p的复散射系数，τm,p表示第m个采样点接收的第p个目标的双程时延。

双程时延可由基于几何光学的穿墙信号模型[12]求得。如图2所示，以天线所在的阵列为横轴，垂直于墙面左侧所在的直线为纵轴建立直角坐标系，利用快速墙体补偿法求墙体表面折射点进而确定回波时延。

图2 基于几何光学的穿墙信号模型

由ΔBA1A2与ΔBxm A3相似，ΔAB1B2与ΔAOB3相似，可得：

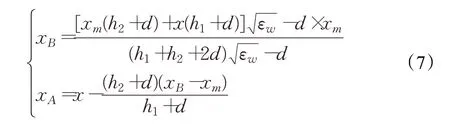
电磁波在穿墙传播时速度会衰减为：

其中，v表示电磁波在墙体内部的传播速度，εw表示墙体相对介电常数。

由穿透墙体时的折射点可确定传播路径，进而求解单程反射时延τ：

当天线沿水平方向位移时，天线到墙体的距离保持不变，因此，墙体回波与传播时延为一固定值，墙体反射回波与天线的测量位置无关，可认为在空域上基本保持不变[13]，则墙体反射回波表示为：

其中，σw表示墙反射系数，τw表示天线到墙体的传播时延。

则雷达在第m个位置第n个工作频点的天线接收信号可表示为：

在TWRI的实际应用中，成像区域内目标个数通常为单个或少数的，因此，穿墙雷达目标信号符合稀疏特性。将成像区域近似看作由一个个网格点组成的二维平面[14]。再把成像场景沿着横轴方向和纵轴方向平均划分为Q个网格点，每一个网格点代表一个像素点，再纵向拉伸，按列排成一个Q×1维矩阵，Q为网格总数，如图3所示为成像区域网格划分示意图。

设sq表示加权指标函数，定义为：

图3 成像区域网格划分示意图

当某一个网格点与目标位置重叠时，则该网格点对应的散射强度值被定义为目标复散射系数σp，否则为0。由于目标仅占据某一部分的网格，则由目标的复散射系数组成的二维反射系数矩阵同样具有稀疏性，将其按列排列堆叠成一个新的一维列向量s，则系统在第m个观测位置处的目标回波信号矩阵可表示为：

其中，Ψm=[ψm(n,q)]是一个由e-j2πfnτmq通过列堆叠而成的N×Q维矩阵，τmq为第m个测量位置到第q个网格的双程反射时延，可由式（9）求得。

将M个测量位置的所有目标回波信号表示为一个MN×Q的矩阵：

同理，处理各个位置的墙杂波信号，系统接收信号组成的字典矩阵表示为：

其中，Zw、Zt和V分别表示墙杂波矩阵、目标回波矩阵和噪声矩阵。

通常探测区域中有用的目标仅占据较少的空间位置，目标信号具有稀疏性，故Zt为稀疏矩阵，只有少量非零元素；而墙体位置相对固定，墙杂波信号在每个天线位置的强度近似相等，具有较强的相关性，则可近似认为Zw为低秩矩阵，只有很少的非零奇异值。

1.3 测量矩阵的构造

本文选择一种简单且易于操作的压缩测量方法，即随机选取天线测量位置，同时随机选取脉冲工作频率进行降采样，则从MN×MN的单位阵中随机选取K行来组成相应的测量矩阵。压缩感知采样示意图如图4所示。

降采样后的数据为：

其中，Φ是测量矩阵，v(Z)表示将矩阵按列堆叠成列向量的运算。

将式（14）、（15）代入式（16）可得：

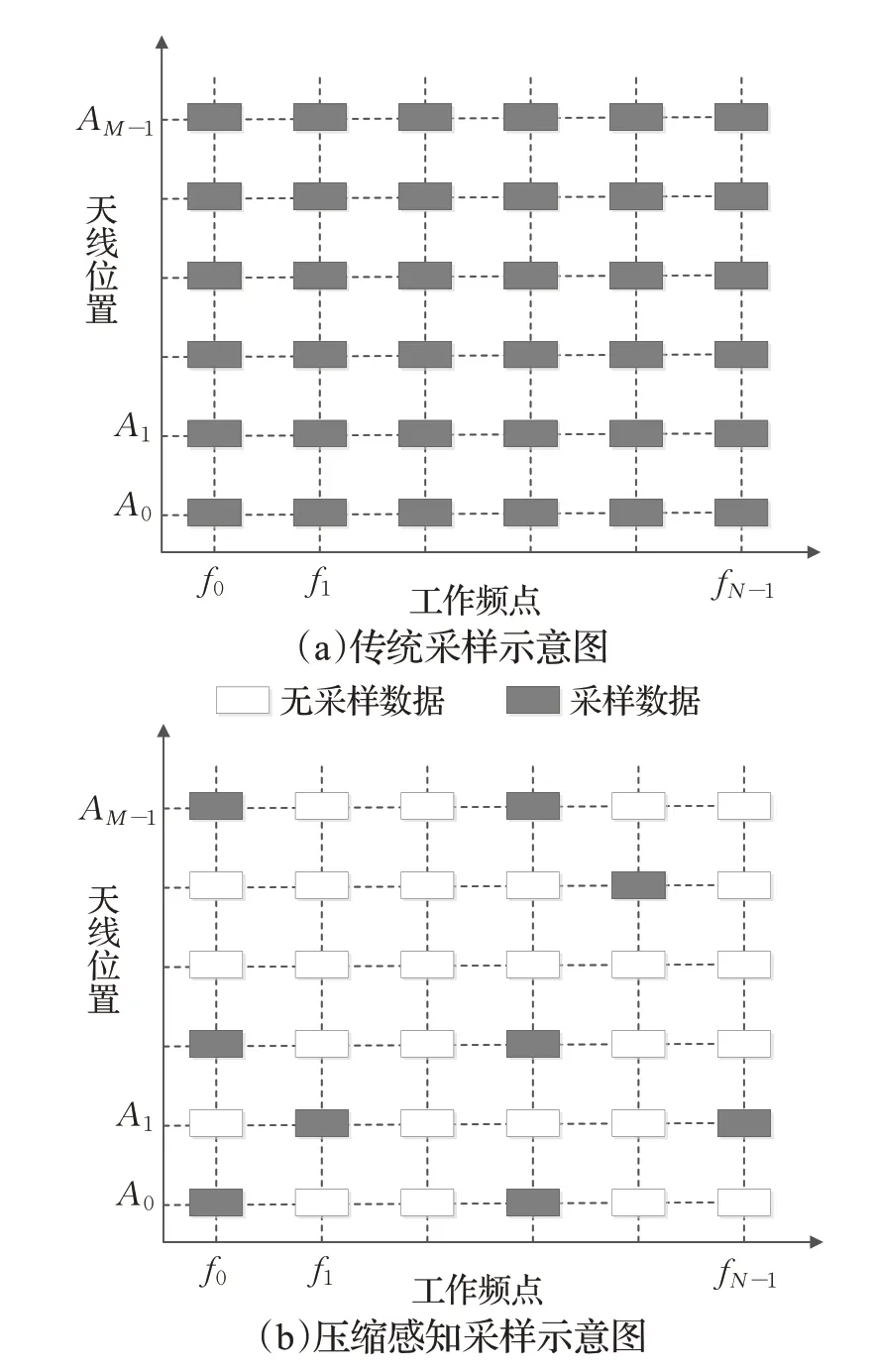
图4 压缩感知采样示意图

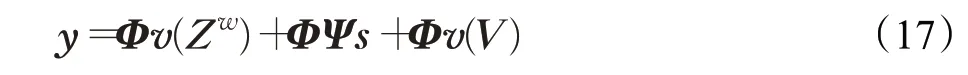
即转化为求一个低秩矩阵和稀疏矩阵的优化问题[15]：

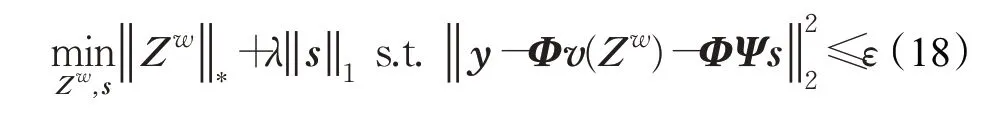
其中，‖‖*表示核范数，‖‖1表示l1范数，ε为重构允许的最大误差，λ为低秩矩阵和稀疏矩阵约束平衡的正则化参数。

针对这样一个含核范数和l1范数的带约束条件的凸优化问题，常采用拉格朗日乘子法构造无约束条件的优化问题：

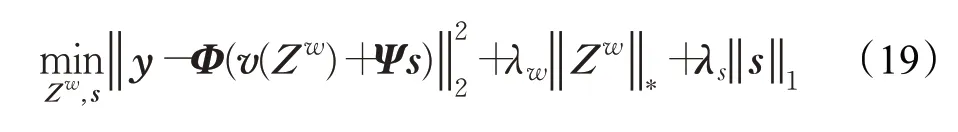
其中，Zw可通过奇异值软阈值法进行求解，s可通过l1范数最小化技术进行计算。λw、λs分别为低秩矩阵和稀疏矩阵的正则化参数。但该方法涉及奇异值分解运算较为复杂，导致阈值迭代速度较慢。

1.4 基于IALM的成像重构

1.4.1 增广拉格朗日乘子法

将一个原始数据矩阵D拆分成一个低秩矩阵A和稀疏噪声矩阵E之和，矩阵恢复模型可通过拉格朗日算法重构，可表示为：

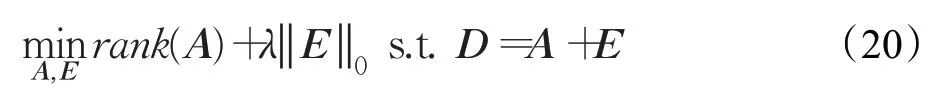
其中，λ表示正则化参数，rank(A)是矩阵的秩函数，一般取（m、n为矩阵的维度数），是高度非线性非凸优化的组合优化问题，没有有效解决方法。通常可通过对目标函数进行凸松弛，将核范数逼近矩阵的秩范数，矩阵的l1范数逼近矩阵的l0范数，从而转换成凸优化问题进行求解：

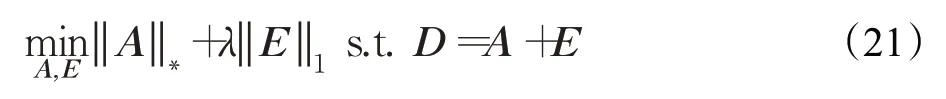
其中，‖‖*表示核范数，‖‖1表示l1范数，λ是调节低秩矩阵和稀疏矩阵的正则化参数。

对于这样一个优化模型，一般可用主成分追踪法、加速近似梯度法、增广拉格朗日法[16]及交替方向乘子法等来求解。

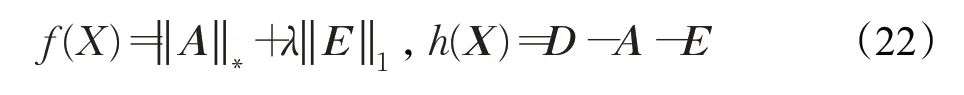
可得到增广拉格朗日函数形式：

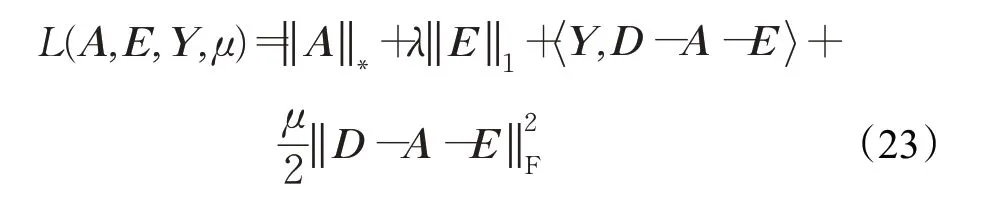
其中，Y表示拉格朗日乘子，表示标准内积，μ代表惩罚系数，‖‖F表示Frobenius范数。

通过迭代的方法将式（23）的最小化公式代入下式进行求解：

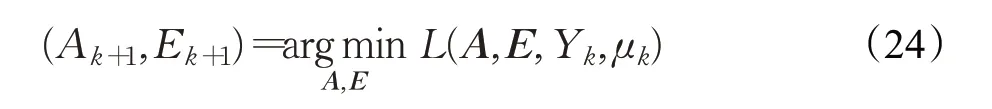
通过多次的交替更新迭代方式可直接求得上式的最优化解，即首先固定E和Y不变，通过运算式（24）最小化条件下的A，再确定A和Y不变，通过函数极小化条件下得到E。通过在每一步的迭代中不断地求矩阵A和E的精确解，最终恢复原始矩阵的方法称为精确增广拉格朗日乘子（Exact Augmented Lagrange Multiplier，EALM）法。

1.4.2 基于IALM的成像重构

在实际迭代过程中，不需要求得A和E的精确值，而只需迭代一次就可恢复原始矩阵的局部最优解，该方法称为非精确增广拉格朗日乘子（Inexact Augmented Lagrange Multiplier，IALM）法。

本文提出采用非精确增广拉格朗日乘子（IALM）法来求解式（18），先固定矩阵S和Y（Y代表拉格朗日乘子），求一个最小化的Zw；接着固定Zw和Y，求一个最小化的S，循环迭代就可得到收敛的最优解。

首先，定义软阈值算子Λλ(Σ)为：

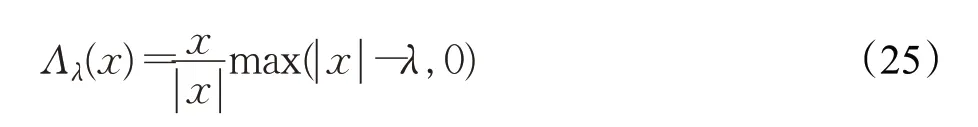
其中，λ为一常数。

矩阵奇异值分解（SVD）定义为：

奇异值软阈值算子（SVT）定义为：

具体迭代步骤为：

（1）参数初始化：

设Z0=v*(Φ†y)，其中v∗()表示矩阵化运算，表示把NM×1维向量转化为N×M维矩阵；Φ†为Φ的伪逆矩阵；Y0=0，S0=0，μ0=0，ρ>1，k=0。

（2）更新Zw：

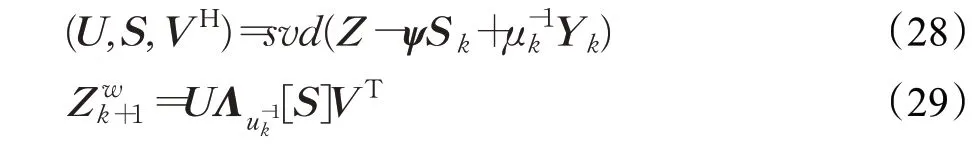
（3）更新S：

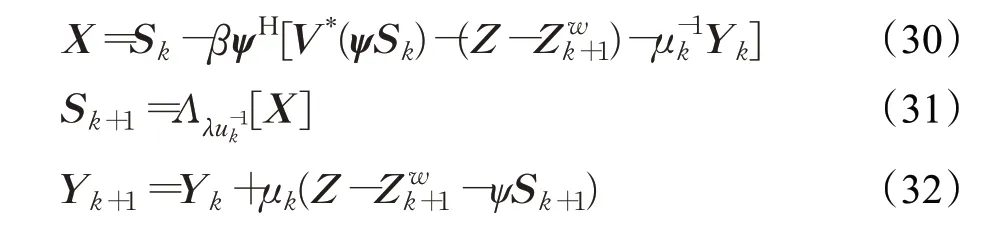
（4）对参数μk进行更新：

令k=k+1，当函数收敛时退出循环。

2 仿真结果分析

为验证本文所提成像算法的有效性和准确性，利用图1所建立的穿墙雷达探测模型进行算法的验证。本文所有仿真实验均在Windows 10系统下进行，成像部分的仿真均在MATLAB R2014a环境下进行。仿真模型设置如下：雷达起始频率fl设置为1 GHz，步进间隔为10 MHz，终止频率fh为3 GHz，则步进频信号共有201个采样频点。合成孔径长度为2 m，每隔5 cm设置一个天线，共有41个天线测量位置。设墙体厚度为0.2 m的混凝土材质，相对介电常数为6，且距离天线0.15 m，墙体散射系数设为1，目标散射系数设为0.1，并加入10 dB噪声。设理想目标位于水平向1 m、距离向2 m处，边长为0.05 m。设置成像区域为3 m×3 m，将成像区域平均分为60×60个网格。从201×41=8 241个频域样本数据中随机抽取出1 648个数据（保证降采样）进行成像。迭代过程中，设置正则化参数λ为0.2，惩罚系数μ为1，ρ为2，1E−6为迭代运算的判断阈值。重构结果均采用归一化到[0，1]区间的图像强度像素值的绝对值来表示。如图5所示为仿真成像结果对比，其中图5（a）为目标真值图，图5（b）为直接CS成像，图5（c）为直接OMP成像，图5（d）为直接ISTA成像，图5（e）为抑制杂波[17]后直接CS成像，图5（f）为抑制杂波后直接OMP成像，图5（g）为抑制杂波后直接ISTA成像，图5（h）为ALM成像，图5（i）为IALM成像结果。

从图5可以看出，在压缩感知框架下利用降采样数据仍能重构目标像，验证了该理论在穿墙雷达成像中具有的利用降维采样数据恢复原始回波信号的独特优势。其中，图5（b）与图5（c）中清晰可见墙体的位置，而图5（d）中墙体回波较弱，不易直接从图中观察到，对比可以看出，利用直接CS成像的效果最差，成像结果中有大量噪声，目标受周围杂波影响较大，目标像分辨率较低，而直接ISTA成像效果最好，但图中目标像的模糊散焦现象较严重。而抑制杂波处理后提高了目标成像质量，其中，分别对比图5（b）与图5（e）、图5（c）与图5（f）可以看出，抑制杂波后目标成像质量更高，说明了很好地消除墙体对目标回波的影响，重构场景中杂波较少，目标像较清晰，图像质量得到了很大的提高，对比图5（d）与图5（g）可看出，目标成像质量基本没有太大的改变，抑制杂波处理的效果不大，说明了抑制杂波对直接ISTA成像提高成像质量影响较小。

而图5（h）与图5（i）成像质量较好，场景中目标散射点成像较清晰，目标旁瓣小，杂波较少，成像精度更高，表明本文所提出的算法在成像同时抑制了墙杂波，在未提前抑制墙杂波的情况下仍能满足成像要求，分辨率有了显著提高，能较清晰地重建目标，有更好的聚焦性能和散射点重构效果。但由于墙体的存在，均会使目标位置与实际位置存在一定程度的偏差，造成目标成像位置的偏移。

为了定量评价成像重建性能，引入信杂比（Target to Clutter Ratio，TCR）和运行时间作为衡量标准。其中，TCR值越大，说明目标重构误差越小，成像质量越好；时间值越小，说明处理速度更快，更符合实际应用中实时性要求。

TCR定义为：

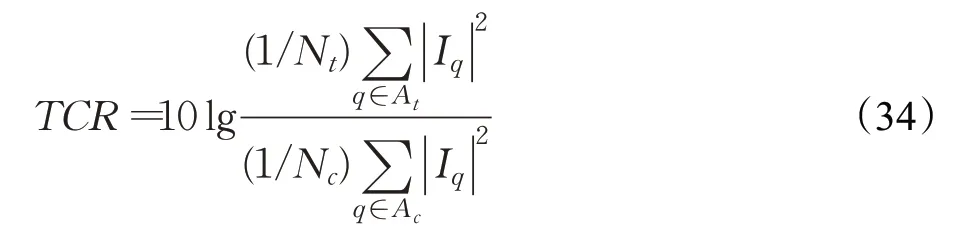
其中，Nt和Nc分别表示目标区域和杂波区域的像素值个数，At和Ac分别表示目标区域和杂波区域，Iq表示成像区域内第q个像素值。

反复进行50次实验求得平均值，统计成像重建性能对比结果如表1所示。

从表1对比看出，各种算法在抑制杂波后均可提高成像质量，但相应地也增加了运行时间。其中，直接CS成像由于调用CVX工具箱，使得运行速度较慢。直接CS成像在未进行墙杂波抑制处理时的TCR最小，说明了成像质量最差，抑制杂波后的TCR提高了约22 dB，但对应处理速度也变慢，平均成像重构时间增加了约2倍，TCR增加了约1倍。直接OMP成像经杂波抑制处理后，平均成像TCR提高了约13 dB，重构时间也相应地增加了约20 s。而杂波抑制处理对直接ISTA成像几乎没有太大的改善，TCR在处理前后大致相等。直接OMP与直接ISTA成像在运行时间上相差不大，但ISTA类算法在此场景下恢复目标信号的信杂比更高。

而本文所提算法的TCR在表1几种处理算法中较高，该算法利用降采样数据重构目标像时，运算速度有所提高，成像质量也有了很好的改善。其中，ALM成像的TCR和IALM成像的TCR相差不大，但处理时间却慢了约4 s，说明所提算法在提高成像质量方面的优势，且可以更好地满足实时性的要求。

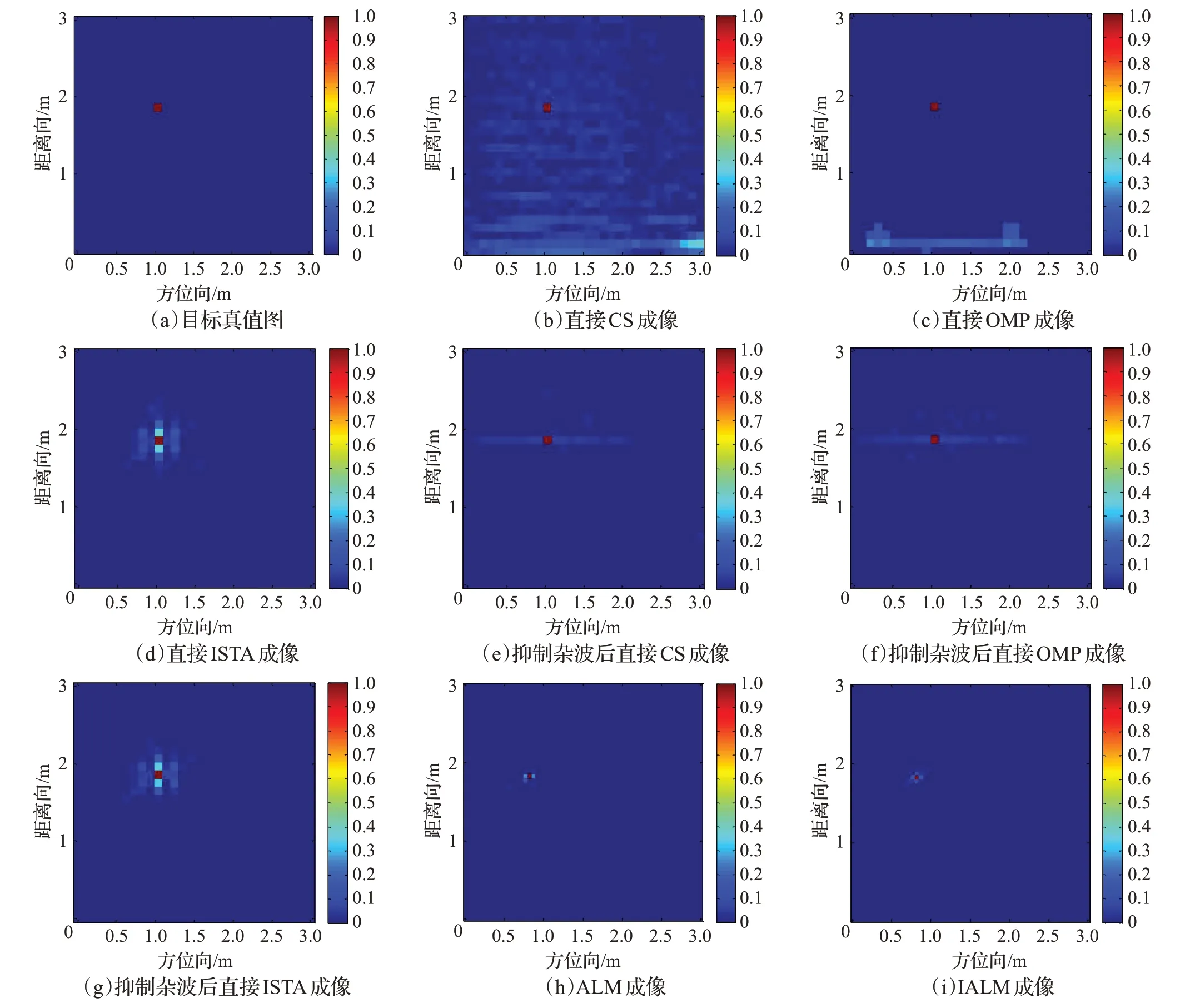
图5 仿真成像结果对比

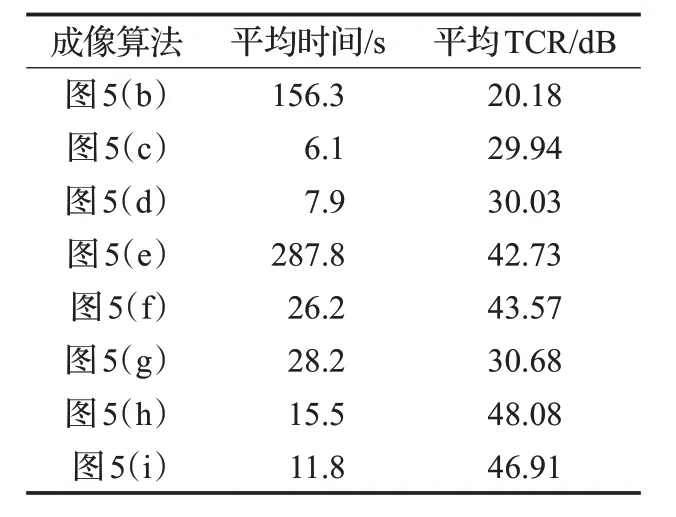
表1 成像重建性能对比

从仿真成像结果和重建性能对比中可看出本文所提算法在对目标成像过程中能够有效地抑制墙杂波，TCR较好，说明信号重建误差较小，重构精度较高，成像质量更高。这是因为本文算法的核心思想是回波信号矩阵分解为含目标散射信息的稀疏矩阵及含墙杂波的低秩矩阵和之和，在算法迭代过程中，很好实现了杂波抑制和目标成像相融合。

3 结束语

本文针对传统CS成像算法的计算过程复杂、对信噪比要求高等不足提出了一种基于CS框架下的非精确增广拉格朗日的穿墙雷达成像算法。该算法将穿墙雷达成像问题转化为一个含核范数和l1范数的复合优化问题，再引入非精确增广拉格朗日乘子法进行迭代求解，数值仿真实验结果表明，相比传统成像算法提高了目标信杂比，且可以有效抑制旁瓣，很好地兼顾了重构精度和计算效率。而在重建过程中正则化参数是基于测量数据的先验信息和重建结果质量的经验尝试判断确定的，因此对正则化参数的设计，将是下一步研究工作的重点。