卫星信道高动态时延与多普勒模拟系统的研究与设计
2021-06-11鲍大志邢斯瑞刁国影
鲍大志,邢斯瑞,刁国影,陈 悦
(长光卫星技术有限公司,吉林 长春 130102)
在卫星通信系统研发和测试阶段,需要分析卫星在轨的实际通信性能. 对于卫星通信来说,实际环境的信道测试难以实现,需要借助信道模拟系统进行测试. 随着软件无线电技术的成熟,信道模拟器普遍采用软件无线电技术实现[1,2].
卫星信道受自由空间损耗、 时延、 多普勒频移、 阴影、 多径等多种因素影响. 其中针对阴影,多径等因素目前已研发出多种描述模型. 但针对目前最为热点的低轨通信卫星,由于通信仰角相对较高,相比于阴影、 多径等因素,高动态的时延和多普勒对信道特性具有更为普遍的影响,但目前针对时延多普勒特性高动态实时模拟的相关研究较少[3-5]. 由于卫星高速运动且通信距离远的特点,使得卫星信道时延与多普勒呈现高动态范围,且快速变化,这种影响在低轨卫星上尤其明显. 高动态特性对卫星通信性能和导航测距等有较大影响[6,7]. 信道模拟系统可以通过先进先出(FIFO)的存储器模拟固定的通信时延,需要的存储器规模与采样率和最大时延量成正比. 针对信号发生器可利用数控振荡器(NCO)调整信号发送速率,模拟高动态时延变化; 通过载波NCO完成多普勒频率控制[8]. 而对于信道模拟器,由于信号形式未知,上述时延控制方法无法使用,需要对时延直接控制. 本文结合存储器控制,可变分数时延滤波器,数字NCO等技术,利用软件无线电实现了卫星信道静态时延模拟、 高动态时延和多普勒的联合实时模拟,并对系统功能进行了验证.
1 系统模型
提出的卫星信道高动态时延与多普勒模拟系统模型如图1所示. 射频输入信号经过下变频和模数(AD)变换模块之后,输出数字基带信号,在FPGA当中完成时延和多普勒特性的实时生成,再经过数模(DA)变换和上变频模块变换,实现射频信号输出.

图1 系统架构Fig.1 System architecture
FPGA中集成了静态时延控制、 动态时延控制以及多普勒频移模拟控制模块. 静态时延控制模块实现FPGA和DRAM之间的数据交换,实现固定延迟. 动态时延控制模块从上位机参数控制模块实时接收时延变化量,计算实时时延,实现实时时延控制. 多普勒频移模拟模块从上位机接收实时多普勒频移量,实现实时多普勒实时模拟. 上位机参数控制模块提供输入频点,输出频点,固定时延参数,实时时延变化量和多普勒频移量等参数信息,并传输到FPGA模块当中.
2 静态大规模时延
信号时延即对信号进行一段时间的缓存后再输出,需要FIFO存储器来实现. 时延越大,信号采样率越高,则需要的存储器容量则越大. 为了满足大范围时延的要求,选择DRAM存储器实现和FPGA的交互. DRAM具有存储空间大,成本低的特点. 但从DRAM存储器读取数据具有不固定的延时,并且DRAM存储器读写不能同时进行.
对于DRAM中的数据,按照地址进行连续读写,到达末尾地址后绕回到首地址,从而实现FIFO结构; 对DRAM采取数据请求和获取的分级形式对数据进行缓存,克服读取延时不确定性; 通过高速时钟(高于二倍采样时钟)进行读写周期切换,并利用FIFO缓存控制读写速度,从而达到等价于读写同时进行的效果. 在时钟周期分配部分,首先写入N个周期,然后读取N个周期,再次写入N个周期,然后读取N个周期……. 通过选择合适的N值,降低频繁的读写切换导致的数据吞吐量降低问题.
具体流程如图2 所示: 建立FIFO 1和FIFO 2,FIFO 1中存储数字信号输入; FIFO 2中存储DRAM输出的数字信号并输出给后续模块处理. 通过判断FIFO中数据存储情况,控制DRAM读写速度,由于读取的延时性,进行DRAM数据请求时,应该保证FIFO 2中留有一定空间余量,余量应大于DRAM最大的读取延迟周期数.

图2 静态时延控制原理Fig.2 Principle of static delay control
3 多普勒频移模拟
对于数字IQ调制信号
s(n)=I(n)+jQ(n),
(1)
式中:I(n)为同向路信号;Q(n)为正交路信号. 要对s(n)进行频率f的变频,则
s′(n)=s(n)ej2πfn=
I(n)cos(2πfn)-Qsin(2πfn)+
j[I(n)sin(2πfn)+Q(n)cos(2πfn)].
(2)
令θ(n)为正弦信号的相位信息,则

(3)
式中:fs为采样频率,n为采样周期计数. 利用式(3) 可计算实时相位信息,根据相位信息,查询存储器中的正弦函数表得到对应的正余弦值. 然后利用式(2)中的乘法器结构,完成数字变频,实现多普勒模拟.
4 精确时延控制
利用FIFO结构实现信号时延,时延分辨率为采样周期Ts. 为了获得更高的时延分辨率,本文基于最小二乘法设计了分数时延滤波器,在滤波器阶数固定的情况下,可保证整个通带内时延误差最小化,最大化利用信道模拟器的采样带宽. 为实现时延实时可变,滤波器采用Farrow结构实现,对于不同的时延输入值,滤波器系数不需要进行重新计算.
简要介绍分数时延滤波器设计方法如下,详细推导过程可参考相关文献[9,10].Hid(ejω)为理想分数时延滤波器频率响应,H(ejω)为分数时延滤波器实际频率响应,设D为时延系数,例如D=0.3则代表延迟0.3个采样周期,则
Hid(ejω)=e-jωD.
(4)
考虑通带内误差最小化,令通带为[0,aπ],在整个通带范围内,频率响应误差函数
hTPh-2hTQ+m,
(5)
式中:h为时域冲激响应系数向量.
在式(5)中,对hT求偏导,使得导数为0得到误差最小值,于是
h=P-1Q.
(6)
计算可得
asinc[a(k-l)],
(7)
asinc[a(i-D)].
(8)
FARROW架构滤波器实现:
分数时延滤波器延时系数为D,滤波器的传递函数定义为

(9)
用M阶多项式进行拟合

(10)
根据式(9),式(10),有
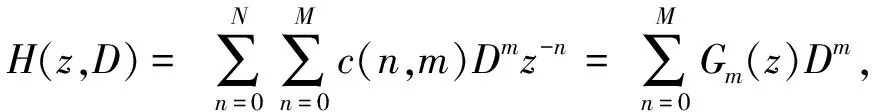
(11)

(12)
Gm(z)可以看成子滤波器的传递函数,整个滤波器结构如图3 所示.
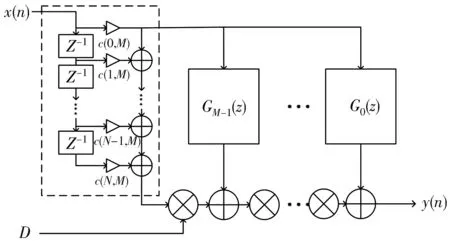
图3 FARROW结构滤波器Fig.3 Farrow structure filter
本文采用3阶多项式拟合的32阶滤波器,通带归一化频率a=0.8,滤波器的幅频特性曲线和时延特性如图4、 图5 所示,时延以采样周期(sample)为单位:
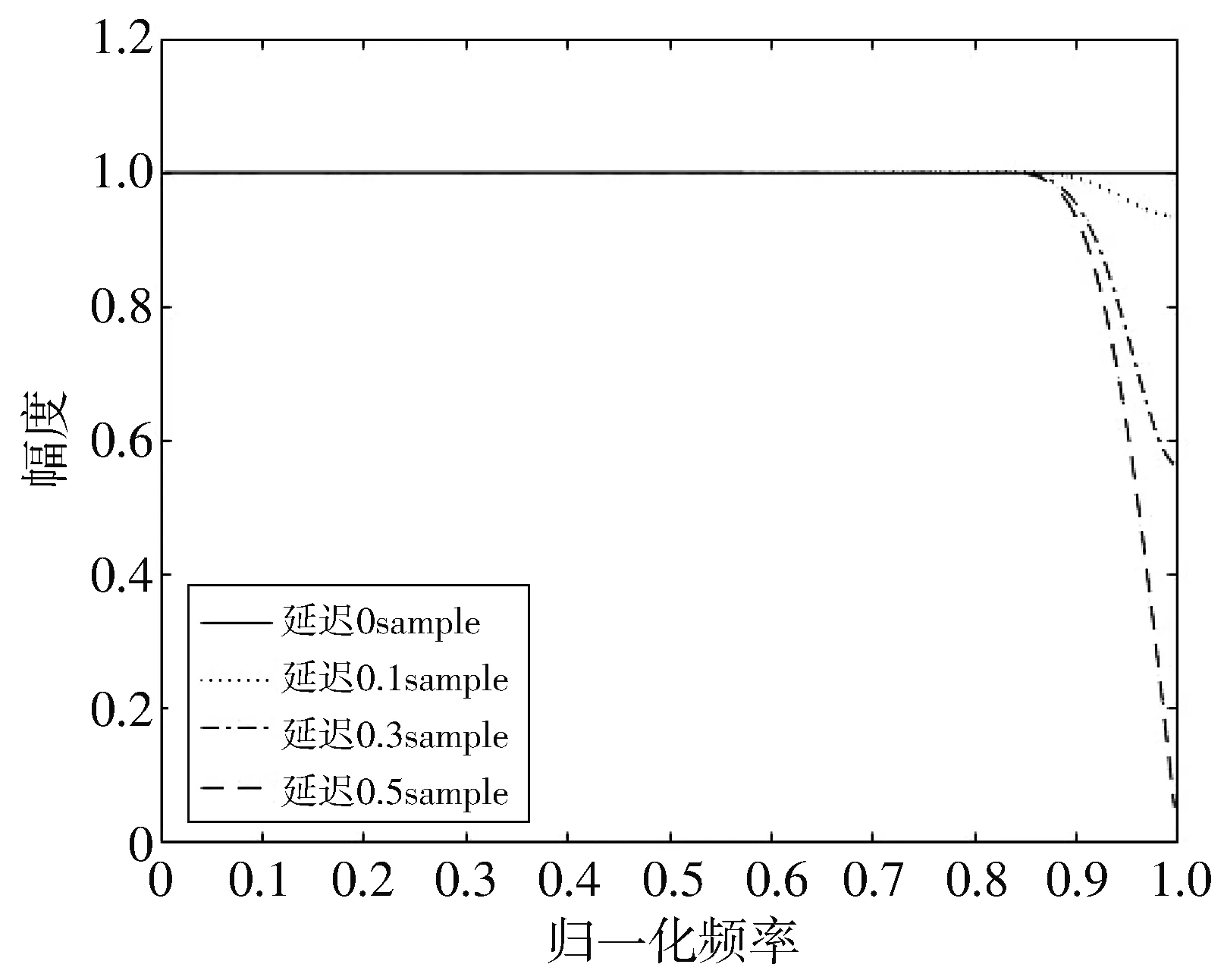
图4 幅频特性图Fig.4 Amplitude-frequency characteristic diagram

图5 时延特性图Fig.5 Delay characteristic diagram
通带内最大幅度误差不超过0.001,通带内最大时延误差不超过0.000 1.
5 动态时延控制
在实际的卫星通信当中,发射机和接收机之间的位置关系持续变化,所以,时延也是动态变化的,需要对时延进行动态连续控制. 控制方式如图2 所示:
FIFO 2中缓存输入数据(即静态时延控制模块中的FIFO 2),FIFO 3中缓存输出数据. 整个循环以略高于采样频率的时钟运行,循环时钟频率越高,则能达到的时延变化率越高,而时延变化率取决于卫星径向飞行速度与光速的比,由于卫星飞行速度远低于光速,所以循环运行时钟略高于采样时钟即可,保证在后续处理中以采样速率读取FIFO 3中数据情况下不会读空. 具体步骤如图6 所示.

图6 动态时延控制原理Fig.6 Dynamic delay control principle
步骤 1) 判断FIFO 2中待读取的数据是否充足,如果是,则执行步骤2),如否,执行步骤1);
步骤 2) 判断FIFO 3中待写入的数据是否充足,如果是,则执行步骤3),如否,执行步骤1);
步骤 3) 所述动态时延控制单元进行动态时延处理,并将动态时延处理后的数据写入FIFO 3,返回步骤1).
动态时延处理部分利用了上文设计的分数时延滤波器:
假设第n个输出时刻的时延为Td(n),采样周期为Ts,令
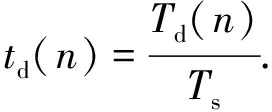
(13)
令ΔTd(n)为第n个输出时刻到n+1个采样时刻的时延变化量,设

(14)
则td(n+1)=td(n)+Δt(n).
(15)
对td(n)进行拆分,令
td(n)=md(n)+kd(n),
(16)
式中:md(n)为td(n)的整数部分;kd(n)为td(n)的小数部分,因为分数时延滤波器的时延范围为 [-0.5,0.5],所以令-0.5
md(n+1)=
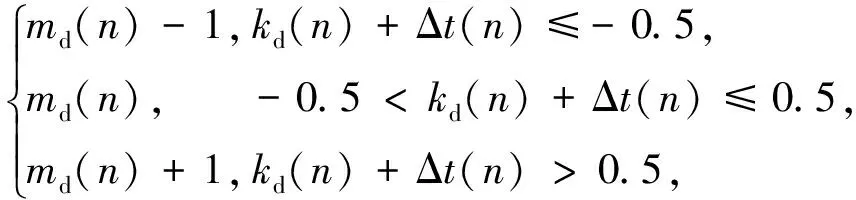
(17)
kd(n+1)=

(18)
当md(n+1)=md(n)时,从FIFO 2中读取数据输入分数时延滤波器,分数时延值设为kd(n),分数时延滤波器输出数据;
当md(n+1)=md(n)+1时,不向分数时延滤波器输入新的数据,分数时延值设为kd(n),分数时延滤波器输出数据;
当md(n+1)=md(n)-1时,连续两周期从FIFO 2数据输入分数时延滤波器后,分数时延值设为kd(n),分数时延滤波器输出数据.
6 上位机参数控制
上位机参数控制单元向下位机传递的一次性参数包括DRAM初始延迟周期n0,分数时延滤波器初始时延值k0,实时参数包括多普勒频移模拟单元中的数字变频器的变频参数d(n),动态时延控制单元中的时延变化量相对值Δt(n),其中n为采样周期计数.
对于确定的传输环境,设初始时刻传播时延值T0,扣除信道模拟器各部分处理的固定时延Tf,得到
T0-Tf=n0Ts+k0-0.5
(19)
式中:Ts为采样周期,由式(19)可计算n0和k0值.

(20)
设fs为采样频率,数字变频器在第n个输出周期的变频参数输入可设定为

(21)
ΔTd(n)为时延变化量,fd(n)为多普勒值,两个参数成正比,设f为通信频率

(22)
可根据多普勒变化值计算时延变化量,动态时延控制及多普勒频移模拟控制模块实时传递参数.
7 性能验证
系统时延和多普勒特性难以直接测试,这给系统的验证带来了困难. 本文通过测距系统,间接对系统的静态时延特性进行验证. 构建直接序列扩频收发信机,通过扩频接收机的锁相环和码环分别对动态时延和多普勒功能进行了验证.
7.1 静态时延验证
系统信号处理存在固有时延,固定延时模块时延也会因为采样时钟偏差和理想结果存在误差,通过配有精确时钟的测距系统,可以对系统时延特性进行测量,从而完成时延特性的校准和性能检验. 本文采用了侧音测距系统进行功能验证[11].
由于系统数据处理需要一定时间,延迟的采样点数不能无限小,令静态时延控制模块延迟点数分别取30 000,100 000,1 000 000,2 000 000,3 000 000,4 000 000,采样率120 MHz,每个延迟点数利用侧音测距系统分别进行10次时延测量,根据测量结果,采用最小二乘法,对系统实际时延性能进行拟合,如图7 所示,得到拟合方程为

图7 静态延迟最小二乘拟合图Fig.7 Static delay least squares fitting diagram
Dr=1.000 003 047 5Di+4.092 9*10-6,
(23)
式中:Dr为系统实际时延;Di为理论时延.
7.2 动态多普勒和时延验证
动态特性利用锁相环和码环验证[12]. 利用锁相环可以跟踪相位变化,锁相环生成的载波可以验证系统的实时多普勒频率模拟性能. 在时延实时快速变化条件下,时延的实时值难以直接监测,但是时延变化将导致信号符号速率发生变化

(24)
符号速率变化量Δp,多普勒频移量fd,时延变化量ΔT3者成正比关系. 而对于直接序列扩频信号,利用码环可以实时跟踪符号速率的变化,从而可以验证系统动态时延控制功能. 码环的具体形式如图8 所示.

图8 码环原理图Fig.8 Code tracking loop schematic diagram
利用伪码生成器生成超前、 即时、 滞后3组伪码,分别对输入数据进行解扩并对解扩后的信号进行积分,利用超前滞后两组伪码的积分结果进行鉴相,鉴相结果经过环路滤波器后利用码NCO调整伪码速率,使得伪码速率和输入数据速率匹配. 因此,在码环结构中可以通过监控码NCO得到符号速率的变化情况,从而验证系统延时的动态变化情况.
本文选择了BPSK调制方式的直列扩频收发信机进行功能验证,符号速率4.096 kbps,码速率3.069 Mbps,扩频码长度1 023. 分别选择常量和线性变化两种形式的多普勒和时延变化形式,得到锁相环和码环的跟踪结果,如图9,图10 所示.

图9 多普勒偏移对比图Fig.9 Doppler frequency shift comparison diagram

图10 符号速率偏移对比图Fig.10 Comparison diagram of symbol rate deviation
跟踪结果和理论值趋势一致,系统有效实现了多普勒频率和时延的实时动态模拟.
8 结 论
时延和多普勒特性是卫星信道的重要特征,在卫星通信系统设计当中需要重点考虑. 本文给出了一种实现信道时延和多普勒特性模拟的有效方法,可以实现大范围高精度的时延模拟,并可以实现时延和多普勒的实时动态控制. 同时,本文给出了系统的测试方案,证明系统的有效性. 本文的卫星信道时延与多普勒模拟系统可以用于卫星通信,导航等系统的测试当中.
