基于Prophet与XGBoost混合模型的短期负荷预测

朱江行，邹晓松，熊炜，袁旭峰,2，艾小清，彭月

（1.贵州大学电气工程学院，贵州省贵阳市 550025；2.贵州电网有限公司电力科学研究院，贵州省贵阳市 550002）

0 引言

在我国高速经济发展中，电力负荷的预测已成为一项重要而艰巨的任务。通过可靠且高质量的负荷预测模型准确地预测电负荷及其变化趋势能够为电网制定调度策略、供电计划提供重要参考[1-2]。

电力系统信息化的发展，分布式电源的大量使用以及电动汽车的出现，增加了配电网中电力消耗的复杂性，对电负荷预测的准确性和稳定性提出了更高的要求。国内外众多学者已对电力负荷预测的理论和方法开展了大量的研究，针对用电负荷的预测，常用的方法主要包括时间序列分析法和机器学习分析法两类[3-4]：时间序列分析方法主要包含指数平滑模型法[5]、自回归方法[6]和累积自回归滑动平均(Auto regressive Integrated Moving Average model，ARIMA)方法[7]等，时间序列分析方法主要根据历史电负荷和现在电负荷预测未来电负荷，但其只考虑了数据的时间相关性因素，并没有考虑外界因素对预测对象的影响，故当有特殊时段时，其预测结果偏差可能较大；机器学习分析法主要包含专家系统法[8]、支持向量机(support vector regression，SVM)[9]、随机森林[10]和人工神经网络(Artificial Neural Network，ANN)[11]等。文献[12]提出了一种基于岭回归估计的径向基函数神经网络短期负荷预测方法，解决了输入多重共线性问题；文献[13]利用改进的PSO-RVM (Particle swarm optimization-Relevance Vector Machine)算法对各小波分量进行预测然后叠加得到最终预测值，为后期运行可靠性评估提供数据支撑，机器学习分析法能够考虑气象、时间及日期等多特征进行预测，提高预测精度。此外也有不少研究人员将多种单一模型进行结合得到混合模型；文献[14]针对负荷数据时序性和非线性的特点，通过卷积神经网络(Cellular Neural Network，CNN)构建多特征向量作为长短期记忆网络(Long Short-Term Memory，LSTM)的输入，将CNN与LSTM有效结合，进一步提高了预测精度；文献[15]采用误差倒数法将LSTM与XGBoost (Xtreme gradient boosting)结合，修正单一模型误差较大的时序数据，以降低单一预测模型误差。

Prophet模型可将时间序列通过一定的函数变换为每小时、每日、每周、每季度及每年等不同时间维度的组合模式，并加以整体趋势[16]，其主要考虑了时间相关性，对气象等因素考虑较少；XGBoost算法运行速度较快，并且通过人为对数据进行预处理，构建考虑气象，日期等多因素的特征向量，考虑了多因素影响[17]。兼顾Prophet和XGBoost各自独有的优点，本文提出一种基于Prophet-XGBoost混合模型的短期负荷预测方法，较单一模型预测精度更高，较SVR模型运行时间更短。

1 Prophet模型

2017-02-24，Facebook发布了时间序列预测框架Prophet，与传统的时间序列预测方法相比，有以下优点：其具有较好的灵活性，轻松适应多个季节的季节性，并通过分析对趋势做出不同的假设；测量值不必呈等间距分布，也不需要插值缺失值；拟合速度较快；预测模型具有易于解释的参数，这些参数可通过分析对预测进行强加。

Prophet实质上是一个基于自加性模型的预测时间序列数据的模型，模型整体可以分解为三个主要部分：趋势项(growth) g (t)、季节项 (seasonality)s(t)、 节假日项(holidays) h (t)，它们通过下式叠加在一起：

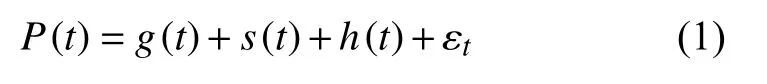
式中：εt代表误差项，一般情况下，假设其服从均值为0的正态分布，其主要用来反映未在模型中体现的异常变动。

g(t)为趋势函数，包括调节模型光滑度的参数和不同程度的假设，主要是对时间序列中的分段线性增长或logistic饱和增长等非周期性变化进行建模，根据数据中的变化点(changepoint)检测趋势走向。本文采用logistic饱和增长模型，基本趋势项采用一个逻辑回归模型：

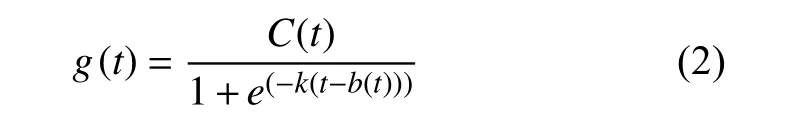
式中：k 代表增长率； b(t) 表 示偏移量；C (t)为模型容量；随着t的 增加， g (t) 趋 近于C (t)。

s(t)代表周期性变化，为了拟合并预测季节的效果，Prophet基于傅里叶级数提出了一个灵活的模型， s(t)可根据以下公式进行估算：

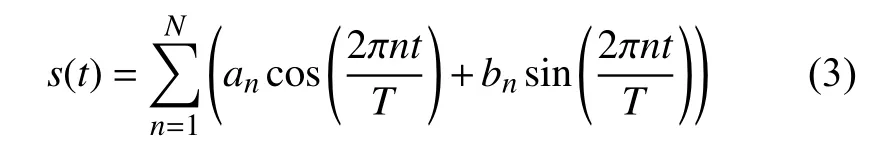
式中： N 代表周期总数； T代表某个固定的周期(年度数据的 T是365.25，周数据的 T 是7)； 2n代表期望在模型中使用该周期的个数； a1,a2,···aN，b1,b2,···bN表示模型中需要估计的参数。

h(t)代表节假日效果，节假日和大事件都会导致时间序列中出现可预测的波动。不同节假日及大事件在不同时刻下的影响都能建立独立模型，给每个独立模型制定一个时间窗口，其中考虑了节假日的影响有窗口期（如中秋节的前几天和后几天），同一个窗口期中的影响为相同值。节假日效果模型 h(t)根据以下公式进行估算：

式中：L为节假日集合；i为 第i节 假日；κi为对应节假日对预测值的影响因子； Di为窗口期中包含的时间t。

定义 Z (t)=[1(t∈D1),···1(t∈DL)]，可得：

1.1 Prophet建模

电力负荷数据具有时序性，本文利用Prophet模型对历史电力负荷数据进行实验，模型构建步骤如下：

1）数据处理。

Prophet的输入量是一个包含两列的数据框，第一列为日期，第二列为与日期相对应的电力负荷数据，本文采用西南地区某地市2013-01-01至2015-12-31日的电力负荷数据，数据的采样周期为1h，包含了每天24个采样点的负荷情况，其中训练集选为2013-01-01到2015-03-13的电力负荷数据，预测目标为2015-03-14日各小时点的电力负荷。

2）参数调优。

在python3.7环境下调用fbprophet软件包，Prophet预测模型中对实验结果影响较大的参数有趋势模型、转折点数量、季节拟合度和假期拟合度。具体步骤如下：

① 选择趋势模型为分段线性的趋势；

② 根据电力负荷数据的规律给参数转折点设定一个初始值为2，选择季节拟合度和假期拟合度的初始值都分别为8和9，并在节假日项中设置节假日特征如表1所示；

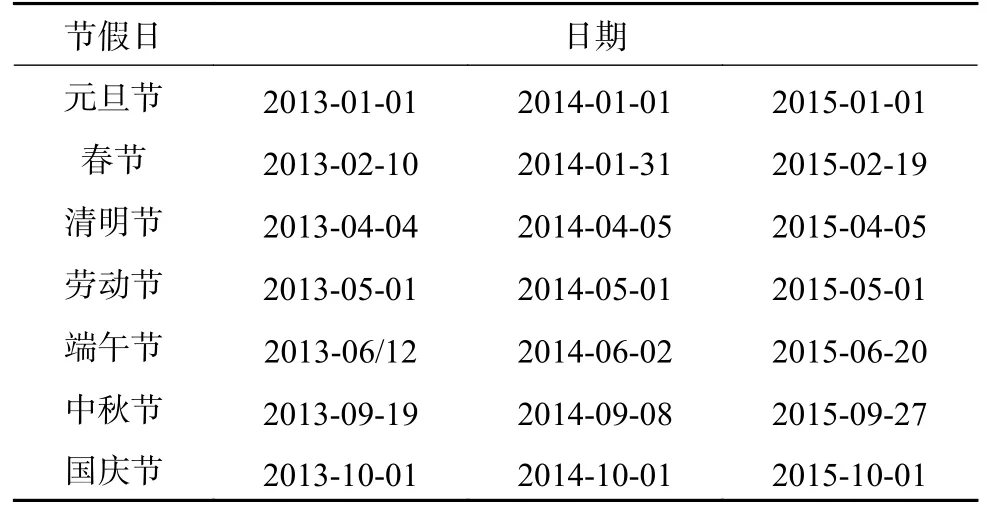
表1 节假日特征表Table 1 Holidays feature list

③ 用处理好的训练集对Prophet模型进行训练，通过作图观察拟合效果，调节上述模型参数，使模型预测效果最佳。

2 XGBoost模型

XGBoost实现的是一种通用的Tree Boosting算法，相比梯度提升算法，性能有10倍以上的提升。所用树模型是回归数（CART）模型，树的集成模型为：

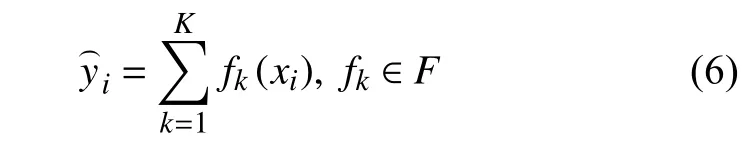
XGBoost模型的目标函数 L包含两部分：

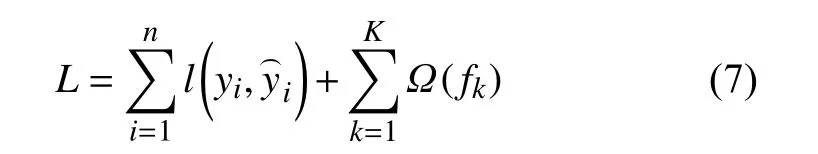
式中：γ 和 λ 为惩罚系数；T 为叶子节点个数；w为叶子节点的分数。

式(7)在计算过程中，通过寻找最佳 ft(xi)，不断叠加来最小化目标函数。第t 轮的目标函数可改写为：

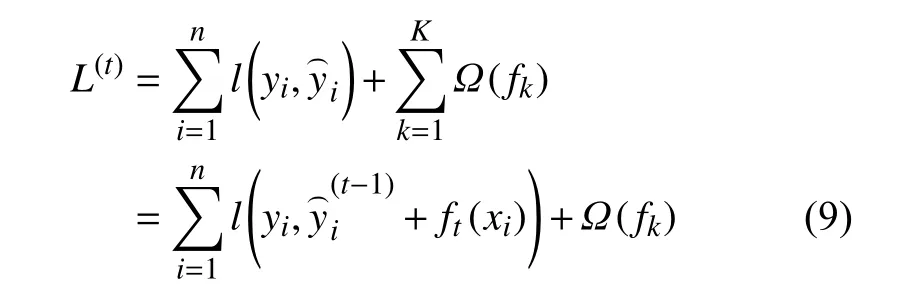
对式(9)进行二阶泰勒近似展开，定义Ij={i|q(xi=j)} 为 第 j棵树每一叶子中的样本集合。其中，为一阶导数，为二阶导数，于是可得：

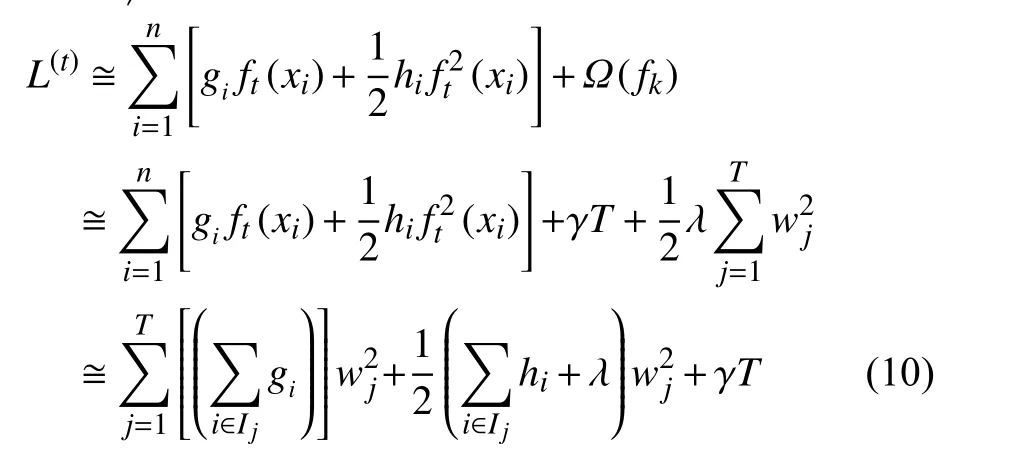
对上式中 w 求偏导可得最优 w为：

将式(12)代入式(11)可得：

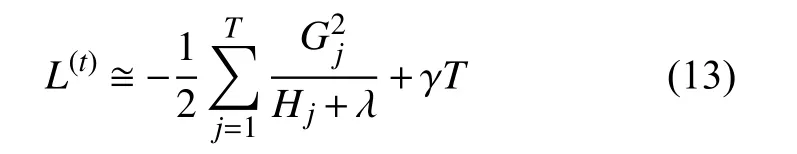
目标函数越小则模型越好，在训练过程中，应用贪心算法对子树进行划分，并枚举可行的分割点，不断计算结点损失以选择增益最大的叶子结点。增益 LGain的计算公式如下：

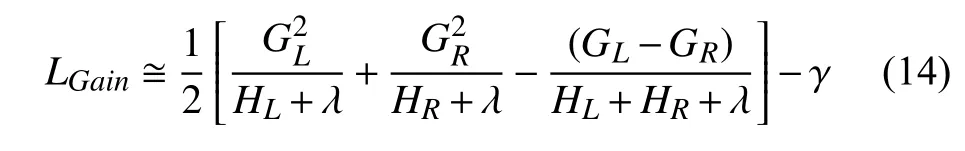
式中：第1项为左子树分裂后的增益；第2项为右子树分裂后的增益；第3项表示不进行子树分裂的增益。

2.1 XGBoost建模

综合考虑气象，日期等因素对电力负荷数据的影响，采用XGBoost模型对电力负荷数据进行预测，模型的构建步骤如下：

1）数据处理。

在1.1节的数据基础上加入气象数据，构建数据集，将前5个时刻的负荷数据，工作日信息，温度，湿度，风速，降雨量构建特征向量作为输入，预测第6个时刻的负荷数据，训练集与预测范围同1.1节。

2）参数调优。

在python3.7环境下调用XGBoost软件包，XGBoost预测模型的参数由3种类型组成， 其中通用参数用于宏观函数控制，Booster参数用于决定每一步的booster，学习目标参数用于控制学习的表现，具体步骤如下：

①确定各个参数初始值及范围如表2所示；

表2 参数初始化值及范围Table 2 Initialization value and range of parameters

②采用网格搜索法对迭代次数、函数、下采样、列占比及学习率进行高负荷搜索，通过观察拟合效果，调整各参数值，如：若过拟合，则减小下采样值，直到达到最好的效果。

3 混合预测模型

根据电力负荷数据分别构建Prophet模型和XGBoost机器学习模型，假设在 t时刻，Prophet模型的预测值为 P(t)，XGBoost机器学习模型的预测值为 X(t)， t=1,2,···,n，然后采用误差倒数法将两个单一模型进行组合。此时，定义集成后的Prophet-XGBoost混合预测模型为：

式中： εP,εX分别为Prophet和XGBoost的平均相对误差； Yt为 t时刻的混合预测值。

应用如式(16)和式(17)所示的倒数误差法求取权重，该方法通过对平均相对误差小的模型赋较大的权重，使整个混合模型的平均相对误差趋于减小，得到更准确的预测值。

基于Prophet-XGBoost混合模型的电力负荷预测流程如图1所示。

图1 Prophet-XGBoost混合模型预测流程Fig.1 Forecasting flow chart of Prophet-XGBoost hybrid model

4 算例分析

4.1 预测评价指标

为评估各预测模型的质量，本文采用平均相对误差(mean absolute percentage error，MAPE)，平均误差(mean error，ME)和均方根误差(root mean square error，RMSE)作为预测评价指标。各评价指标的计算方法如下：

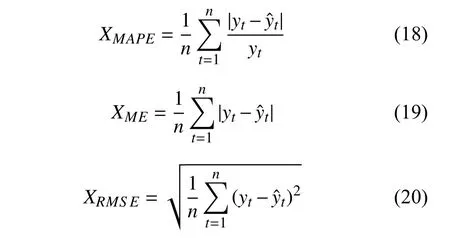
式中：yt代 表t时 刻电力负荷值实际值；代 表t时刻电力负荷预测值；n代表电力负荷数据数量。

4.2 实验结果与分析

本文采用西南地区某地市2013-01-01至2015-12-31的电力负荷数据、气象数据、工作日数据，分别采用1.1节和2.1节所述方法对Prophet模型和XGBoost模型进行参数调优，各最优参数如表3、表4所示。

表3 Prophet模型各参数最优值Table 3 Optimal values of parameters in Prophet model

表4 XGBoost模型各参数最优值Table 4 Optimal values of parameters in XGBoost model

通过实验，式(1)中趋势项、季节项、节假日项3部分对应的分析结果如图2所示，图2（a）至图2（b）依次为总体增长趋势、节假日项、日周期趋势。

由图2可知，该地区电力负荷呈现上升趋势，各节假日对电力负荷的影响程度不同，从日趋势来看，白天用电量多于夜晚用电量，符合实际情况。

混合模型与各单一模型的预测值和实际值的对比如图3所示，各模型的平均相对误差如图4所示，MAPE、ME和RMSE值如表4所示。

图2 组成成分分析Fig.2 Component analysis

图3 各模型预测曲线对比图Fig.3 Comparison of forecasting curves by various models

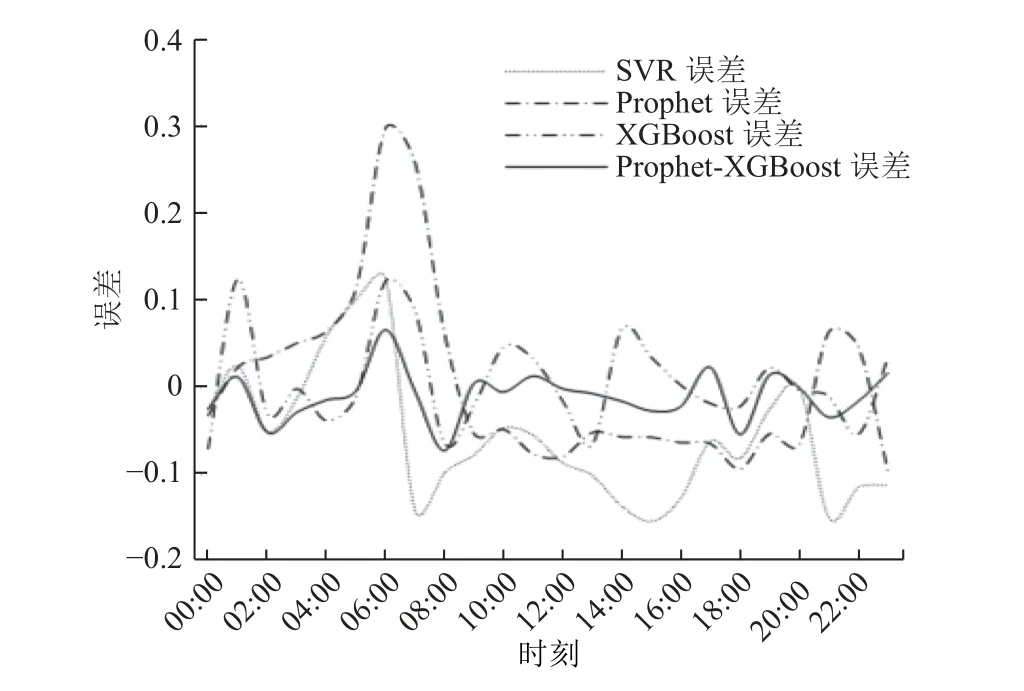
图4 各模型平均相对误差对比Fig.4 Comparison of mean relative error by various models

由图可3知，各模型对次日实际负荷预测都得到较好的结果，其中本文所提出的Prophet-XGBoost混合预测模型相比三个单一模型有更高的预测精度，其预测曲线与实际曲线变化趋势相似，Prophet模型较XGBoost模型精确度更高，SVR模型精确度最低。由图4可知本文提出的Prophet-XGBoos混合预测模型各时刻平均相对误差较小且波动不大，有效降低了预测误差，表现出更好的预测效果。由表5可知，与SVR模型，单一Prophet模型和XGBoost模型相比，Prophet-XGBoos混合预测模型具有最小的MAPE、ME及RMSE值，分别为5.3%、2.643 MW和1.625 MW。与SVR模型相比，Prophet-XGBoos混合预测模型运行时间缩短了60%，大大提升了预测效率。

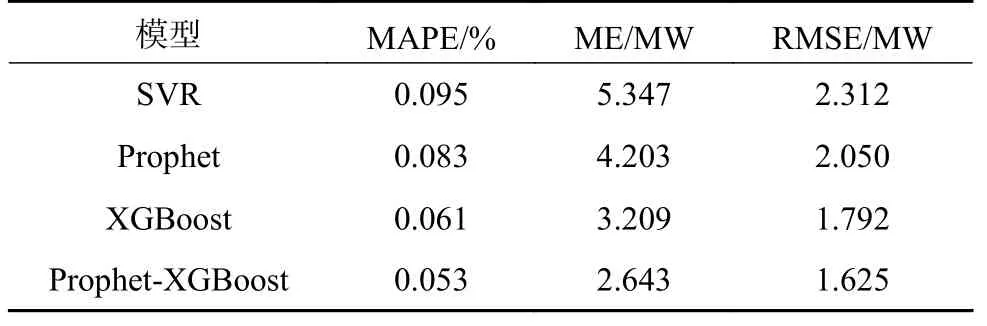
表5 MAPE、ME和RMSETable 5 MAPE、ME and RMSE

5 结论

1）混合模型中的Prophet模型对数据中的趋势变化点和节日效应具有出色的适应能力，尤其对大量的异常值、缺失值和趋势转变的鲁棒性极强，降低了数据波动性对预测的不利影响。

2）应用误差倒数法将Prophet模型和XGBoost机器学习模型进行结合得到Prophet-XGBoost混合模型，其兼顾了两个单一模型各自的优点，弥补了单一模型预测误差较大的缺陷，该混合模型达到了提升短期负荷预测精度的效果。