通货膨胀、预期通货膨胀和产出缺口长期关系研究

李冬冬

摘要：为研究中国目前的经济是否存在菲利普斯现象，文章利用1998～2018年的数据，结合HP滤波法、AR模型和VAR模型进行了实证分析。结果表明，中国的预期通货膨胀和产出缺口均对实际通货膨胀具有一定的解释作用。具体来说，产出缺口与通货膨胀在短期内存在较强的菲利普斯现象，长期则不明显。预期通货膨胀与通货膨胀间存在较弱的菲利普斯现象，但该现象持续时间有可能较长。

关键词：菲利普斯曲线;奥肯定律;通货膨胀率;预期通货膨胀率;产出缺口

菲利普斯曲线是由A.W.菲利普斯提出，表明在英国的数据中失业率和工资膨胀率之间的存在一种负相关关系。后来的经济学家对原始的菲利普斯曲线做出了改进，如用价格的膨胀代替工资膨胀、将预期和供给冲击纳入考察范围，是现代菲利普斯曲线。现代菲利普斯曲线的表达式为：Π=Π0-β（u-u0）+v，其中Π为通货膨胀率，Π0是预期通货膨胀率，u是失业率，u0是自然失业率，β（β>0）是失业缺口对通货膨胀的弹性。奥肯定律描述了GDP变化和失业率变动的关系，其中ΔGDP=实际GDP-潜在GDP，Δu=自然失业率u-潜在失业率u0。按照奥肯定律，GDP每增长1%，失业率便会下降0.5%。鉴于这种此消彼长的关系，可以将菲利普斯曲线改写为Π=Π0+α（Y-Y0）+v，其中Y为实际产出，Y0为潜在产出，α（α>0）为产出缺口对通货膨胀的弹性。另外，供给冲击来自供给方面并影响供给数量的有关因素的变动，如技术进步、中东石油提价、干旱、罢工、战争等。

现有的有关菲利普斯曲线实证研究的文献中，HP滤波法、ARMA模型和VAR模型均是常被用的方法，但综合利用这三种方法的文献则很少。因此，本文将这三种方法结合起来，就通胀率、预期通胀率和产出缺口三者的关系，即在中国是否存在菲利普斯现象进行实证分析。由于近年来，中国在供给冲击方面表现不明显，故下文不予考虑。以下数据均来自于《中国统计年鉴》。

一、产出缺口估计

选取中国1985～2018年的实际产出并进行对数化处理，记为GDP（p78=100）。其中，GDP为一阶单整序列，一阶差分（记为DGDP）后在1%的显著性水平上平稳，1%显著性水平所对应的t值为-4.273277。由于DGDP平稳，且代表的是GDP年增长率的变动，故利用HP滤波法将GDP增长率的变动分解为趋势成分和周期成分，趋势成分记为Hptrend01，周期部分为产出缺口的变动，用来代表菲利普斯曲线中的产出缺口，记为DGDP1（DGDP1= DGDP- Hptrend01）。

进一步地，对产出缺口的变动DGDP1做单位根检验发现，DGDP1在1%的显著性水平上是平稳序列，且1%显著性水平所对应的t值为-2.664853。

二、预期通货膨胀率估计

（一）数据选择和预处理

选取1985～2018年的消费者价格指数（P78=100）并进行对数化处理，记为CPI。其中，1986～1989年、1991～1994年数据缺失，缺失的数据分别用各自临近两年的CPI均值填补。

适应性预期理论认为，人们通常根据以前年度的通货膨胀率来预期未来年度的通货膨胀率，而时间序列模型可以根据以前年度数据做出预测，因此以下就通货膨胀率CPI运用ARMA模型估计预期通货膨胀率。

（二）AR模型构建和检验

1. 模型的判断和最大滞后阶数确定

对CPI做单位根检验，发现其在5%的显著性水平上是平稳的，5%显著性水平所对应的t值为-3.574244。对于平稳时间序列，ARMA模型可根据样本自相关函数、偏自相关函数的截尾、拖尾性来判定模型的阶数。若偏自相关函数是截尾，自相关函数是拖尾，则适用于AR模型;若偏自相关函数是拖尾，自相关函数是截尾，则试用于MA模型;若偏自相关函数和自相关函数均是拖尾，则适用于ARMA模型。CPI0相关图和偏相关图见图1。由图可知，CPI相关图拖尾，偏相关图二阶结尾，初步判定为AR（2）模型。

为更加准确地确定AR模型的最大滞后阶数，分别建立AR（3）、AR（2）和AR（1）模型，通过比较AIC、SC、HQ和最大滞后阶数所对应的p值，选择最大滞后阶数显著且AIC、SC、HQ最小的形式，建立AR（4）模型。

2. AR（4）模型的检验和预测

AR（4）的估计结果为：CPI=1.0316+ 0.9058*CPI（-1）-0.2800*CPI（-2）- 0.1703*

CPI（-3）+0.3854*CPI（-4）。对所建立的AR（4）模型的残差序列进行LM检验，滞后阶数自动选择为2，发现该模型在10%的显著性水平上不拒绝原假设（Pro.为0.8212），即残差无序列相关。

进一步，对残差序列进行异方差检验（ARCH检验），滞后阶数自动选择为1，发现该模型在10%的显著性水平上不拒绝原假设（Pro.为0.7383），即残差无ARCH形式的异方差。由此，可知AR（4）模型估计结果可靠，利用该模型估计预期通货膨胀，记为CPIF。

三、VAR模型的构建

（一）单位根检验和最优滞后阶数确定

由前文可知，通货膨胀率CPI和产出缺口DADP1 是平稳的，这里对预期通货膨胀CPIF进行ADF检验，滞后阶数选择3，发现CPIF在1%的显著性水平上是显著的，并且1%显著性水平所对应的t值为-4.356068。

在此基础上，以CPI、CPIF和DADP1建立無约束的VAR（P）模型，并根据AIC、SC和HQ准则确定模型最优滞后阶数为1，由此建立VAR（1）模型。

（二）模型稳定性检验和Granger因果检验

对所建立的VAR（1）模型进行特征根检验，发现所有特征根都在单位圆内，特征根的模分别为：0.897801、0.669220和0.254638，均小于1，VAR模型稳定。

进一步，对VAR（1）模型进行Granger因果检验，滞后阶数选择1，检验结果见表1。格兰杰因果关系检验实质上是检验一个变量的滞后变量是否可以引入到其他变量的方程中。一个变量如果受到其他变量的滞后影响，则称它们具有Granger因果关系。

1.CPI和CPIF

由该表可知，在5%的显著性水平下，CPI是CPIF的Granger原因，但CPIF不是CPI的Granger原因。这说明CPIF能够较大程度地被过去的CPI解释，CPI的滞后变量对CPIF具有较好的预测作用，这符合适应性预期中人们往往根据过去的价格预期未来通货膨胀率的思想。而CPI不是CPIF格兰杰引起的，说明CPI不能较大程度地被过去的CPIF解释。

2.DGDP1和CPI

在10%的显著性水平下，DGDP1是 CPI的Granger原因，但CPI不是DGDP1的Granger原因。这说明，CPI能够较大程度地被过去的DGDP1解释，这说明CPI和DGDP1很有可能存在某种相关关系。而DGDP1不是CPI格兰杰引起的，说明CPI的滞后变量对DGDP1没有很好的解释作用，这说明价格因素与产出缺口很可能不存在相关关系。

3.DGDP1和CPIF

在10%的显著性水平下，DGDP1不是CPIF的Granger原因，CPIF也不是DGDP1的Granger原因。这说明，DGDP1和CPIF的滞后项都没有对对方起到很好的解释作用。由此，Granger因果性检验说明CPI、CPIF和DGDP1三者之间至少存在着单向Granger因果关系，满足VAR模型的建立前提。

（三）脉冲响应

结合模型的回归结果和本文的研究目的，选择选择第一个方程：CPIt=1.0325+0.6281CPIt-1+0.2089CPIFt-1+0.1195DGDP1t-1。以下运用脉冲响应函数和方差分解对该方程做出解释。

脉冲响应函数描述的是VAR模型中一个内生变量的冲击给其他内生变量所带来的影响，随着时间的推移，观察模型的各变量对于冲击式如何反应的。根据Granger因果检验，在5%的显著性水平下，CPI是CPIF的Granger原因，而在10%的显著性水平下，DGDP1是 CPI的Granger原因。据此，做CPIF对CPI和CPI对DGDP1的响应分析。分别给CPIF和CPI一个标准差的冲击，脉冲响应见图2和图3。图中，横轴表示脉冲响应函数的追踪期数，纵轴表示因变量对解释变量的响应程度，实线为响应函数的计算值，许仙为响应函数值加或减两倍标准差的置信带。

在CPIF对CPI的脉冲响应中，当CPI给CPIF一个标准差息的冲击时，CPIF的响应在前三期是正响应，且不存在时滞，第一期便出现最大正向冲击0.0135，此后响应逐渐减弱至第八期达到最低点-0.005，期间第三期响应为0。第八期后CPI的冲击力度有所提升，CPIF的响应随之缓慢提升但都小于0，最后逐渐收敛于-0.0007。由此可知，通货膨胀的发生在短期内会先对通货膨胀预期产生正向的影响，而在长期内正向影响将转为负向影响，并且这种负向影响随着时间越来越小并收敛于某一数值。这很有可能表明，当现实通货膨胀率提高时，短期内人们会相应地提高对价格的预期，但长期内人们却会降低对通货膨胀的预期。

在CPI对DGDP1的脉冲响应中，当DGDP1给CPI一个标准差息的冲击时，DGDP1前6期的响应为正，7～10期响应为零，11～14期响应为-0.001，15期以后逐渐收敛为零。DGDP1的响应存在一期的时滞，并且于第2期开始出现并达到峰值0.016，此后陡然下降（第3期开始下降速度有所减缓）至第7期零响应。这说明产出缺口在短期内对通货膨胀具有正向影响，但是在长期内，产出缺口的变动对通货膨胀近于零影响。

（四）方差分解

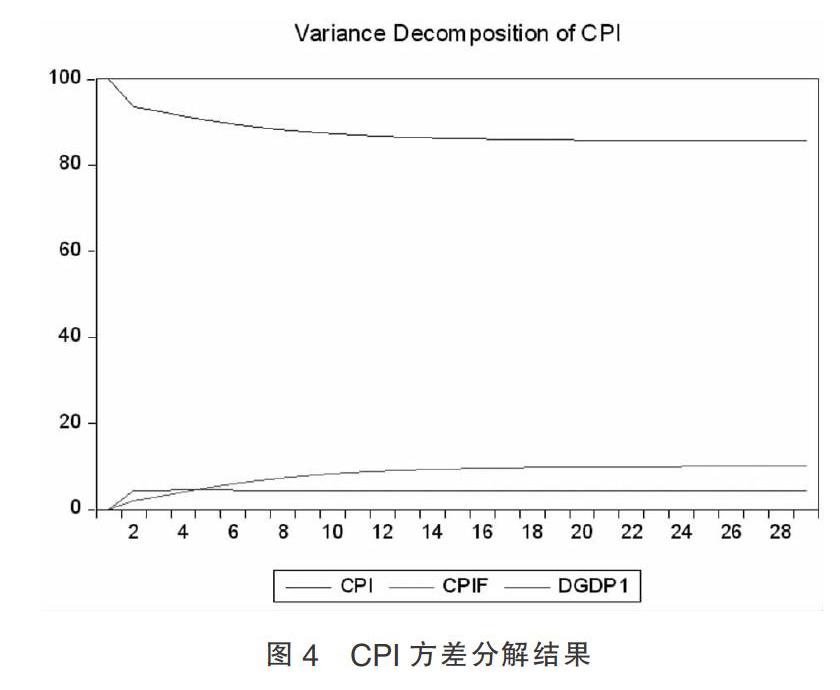
方差分析是通过分析每一个结构冲击对内生变量变化（通常用方差来度量）的贡献度，进一步分析不同结构冲击的重要性。结合本文的研究目的，这里主要对CPI做方差分解，结果见图4。由图可见，CPI对自身的方差贡献率是最大的，尤其是第一期，CPI的方差贡献率完全是由自己所贡献。CPI对自己的方差贡献率在第1期后有所下降，并第14期开始稳定保持在86%。CPIF和DGDP1对CPI的方差贡献率在第1期后均有所上升，其中，CPIF对CPI的方差贡献率于第16期开始稳定保持于10%，DGDP1对CPI的方差贡献率于第2期后稳定保持于2%。另外，前5期DGDP1对CPI的方差贡献率大于CPIF对CPI的方差贡献率，之后则刚好相反。

由此可知，虽然CPI的变动主要由其自身的变动来解释，但是CPIF和DGDP1均对CPI的变动有一定的解释作用。并且，长期来看，CPIF对CPI变动的解释大于DGDP1其变动的解释。

四、结论与启示

综上，CPIF和DGDP1均能够解释CPI的部分变动。并且长期来看，CPIF对CPI变动的解释大于DGDP1其变动的解释。具体分析如下：

研究时段内产出缺口与通货膨胀的关系存在较强的短期的菲利普斯现象。具体来说，Granger因果检验表明DGDP1的滞后变量对CPI具有解释作用，DGDP1对CPI的脉冲响应分析进一步地说明了短期内DGDP1对CPI具有正向作用，但在长期这种作用接近于零。

研究时段内预期通货膨胀与通货膨胀的关系存在较弱的菲利普斯现象，且该现象可能持续时间较久。这是因为，Granger因果检验表明CPI不能够很好地被过去的CPIF解释，但CPI的方差分解说明，CPIF对CPI方差贡献率在长期趋于10%。因此，可以认为，CPIF的滞后项仍是能够一定程度上解释CPI，但解释能力有限。另外，由CPIF对CPI方差贡献率在长期稳定在10%可以推测，长期内CPIF仍可能影响CPI。

另外，由Granger因果检验可知，CPI是CPIF的Granger原因，结合CPIF是对CPI的脉冲响应图，可以发现实际通货膨胀率在短期内会对预期通货膨胀率产生正向作用，长期则转为负向作用。

总之，短期內虽然预期通货膨胀部分的菲利普斯现象较弱，但经济运行仍存在较强的菲利普斯现象，经济的增长（失业率的降低）伴随着价格的快速上升。而长期内，经济中存在较弱的菲利普斯现象，此时经济的增长（失业率的降低）伴随着通货膨胀的轻微上升，两者之间的矛盾不明显。综合以上两点，政府在进行宏观调控时，制定短期内追求匀速增长，长期内追求加速增长的政策目标是较为明智的。

参考文献：

[1]N.格里高利.曼昆.宏观经济学[M].北京：中国人民大学出版社，2011.

[2]马秀远.现代菲利普斯曲线在中国的实证分析[J].市场周刊（理论研究），2008（03）：80-81.

[3]薛荣久，王绍熙，刘舒年，等.当代国际贸易与金融大辞典[M].北京：对外经济贸易大学出版社，1996.

[4]宋则行.现代西方经济学辞典[M].沈阳：辽宁人民出版社，1996.

[5] 张晓峒.计量经济学基础[M].天津：南开大学出版社，2014.

[6] 陈瑶.考虑流动性风险的ARMA模型在股票收益率中的应用研究[J].河南科学，2014，32（04）：655-659.

[7]高铁梅.计量经济分析方法与建模——EViews应用及实例[M].北京：清华大学出版社，2005：281-282.

[8]王周伟，崔百胜，朱敏.经济计量研究指导[M].北京：北京大学出版社，2015.

（作者单位：海南师范大学经济与管理学院）