利用速度相图法求解多次连续碰撞问题

李开玮

(广东理工学院 工业自动化系，广东 肇庆 526100)

在弹性碰撞问题中，一般遵循动量守恒和能量守恒，该类问题目前已有许多解法和讨论[1-3]，而在某些情况下，两物体甚至会发生多次连续碰撞，极大地增加了问题的复杂程度.两物体发生多次碰撞的问题一般可以分为两类：1)求解结束碰撞后，两物体的速度；2)求总碰撞次数.对这类问题若采用代数计算的方法，需要对每次碰撞应用动量守恒和能量守恒列方程组，而且要根据两物体速度判断后一次碰撞是否能够发生，过程复杂，计算繁琐，易忽略细节导致出错.学生在解答该类问题时常有错误.2003年G.Galperin利用坐标相空间的方法讲述了两滑块发生多次连续碰撞时，当滑块质量之比满足100N时，碰撞次数与圆周率有趣巧合的现象[4].更进一步，文献[5]采用速度相图的角度也分析了这个现象，得到结果与G.Galperin一致.本文从另一个角度深入讨论连续碰撞的问题：当两滑块碰撞次数确定时，滑块应满足什么条件，碰撞结束后，两滑块的运动状态又如何？通过采用速度相图的方法，画出了两物体的速度矢量轨迹，对轨迹跟踪并结合圆的几何特点，不仅得到滑块应满足的条件，也得到了结束碰撞后两物体的运动状态，两物体的运动过程清晰直观，计算简化.接下来以一道具体问题的分析来详述这一方法.

1 问题

如图1所示，质量为m2的光滑斜面放在光滑水平面上，一个质量为m1的小球从斜面上h高度处自由下滑，水平面的右端有一固定弹簧，求小球与弹簧只发生n次相互作用，m1/m2应满足的条件？

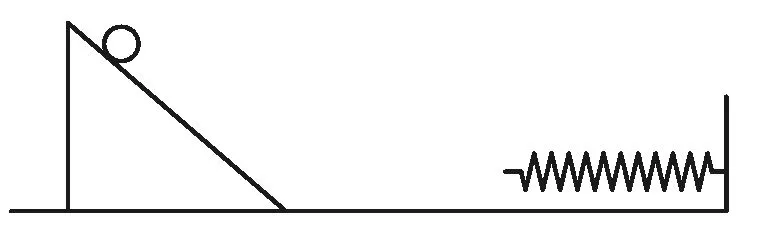
图1 示意图

分析：初始时，小球沿斜面下滑，斜面向左运动，两者在水平方向动量守恒，当小球滑到斜面底端，小球与斜面动能之和为m1gh，随后小球向右运动与弹簧第1次发生作用，之后小球离开弹簧向左运动,若小球速率大于斜面滑动速率，小球将冲上斜面，经过一段时间又滑落斜面，若滑落斜面时小球速度方向向右，小球能与弹簧发生第2次作用，之后与前面过程类似，若满足条件,将与弹簧发生第3、4、5……次作用.

根据以上运动过程分析，小球只与弹簧发生n次相互作用的条件是：1)前n-1次均能与弹簧发生作用；2)第n-1次作用后，小球向左运动速率大于斜面的速率，且小球冲上斜面再滑落斜面后，小球速度向右；3)小球不与弹簧发生第n+1次作用，其条件为：第n次作用后，小球向左运动速率小于等于斜面的速率，或者小球冲上斜面再滑落斜面时，小球静

止或速度仍向左.

通过以上分析，若该问题采用一般方法计算，则在每次小球与弹簧作用后，需对小球与斜面相对运动列出动量守恒与能量守恒的方程组，解出两物体速度，判断小球是否能与弹簧发生下一次作用，其计算十分复杂.接下来我们采用速度相图法求解该问题.

2 速度相图法求解

以水平向右为速度正方向，设m1与m2速度分别为u、v，小球每次向左冲上斜面，之后又滑落斜面，这个过程中小球与斜面组成的系统水平方向动量守恒.另外由于小球与弹簧作用后未损失动能，故小球冲上斜面前与小球滑落斜面后，小球与斜面动能之和均为m1gh.故有

(1)

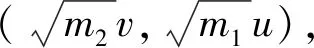
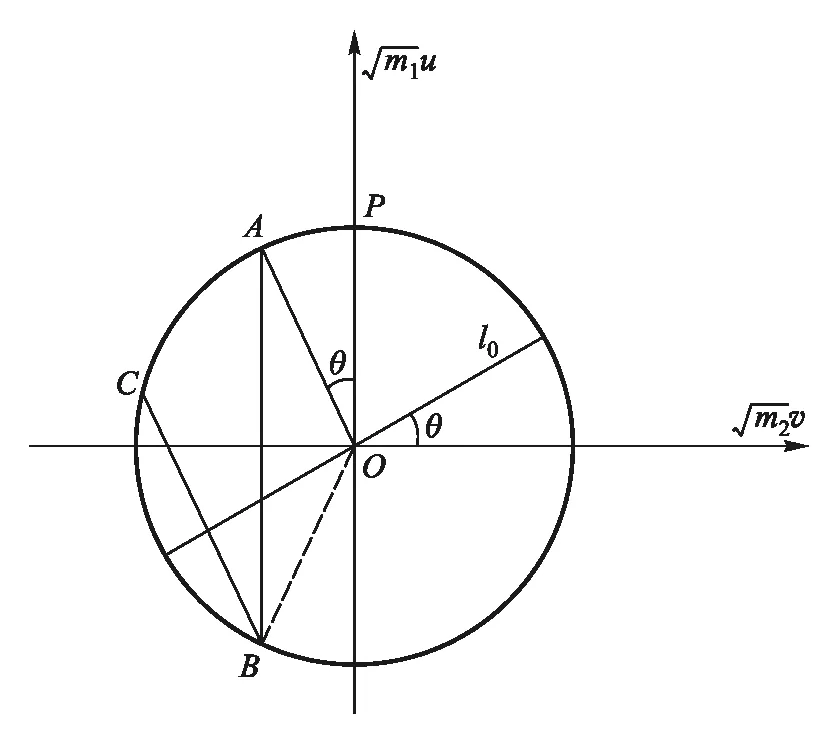
图2 速度相图轨迹跟踪

初始时刻小球与斜面均静止，故速度矢量位于图中O点，当小球到达水平面时，小球速度向右，斜面速度向左，矢量移动到A点，根据式(1)第一个式子可知直线OA斜率为

(2)

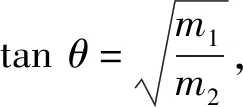
(3)

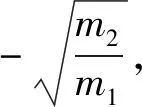
(4)

因此小球与弹簧发生第2次作用，需同时满足条件式(3)、式(4)，而式(4)是式(3)的子集，因此只需满足条件(4)即可.接下来依此类推，小球与弹簧发生第n次作用的条件为

(5)

当n>2，式(5)为式(4)的子集，因此式(5)能保证前n-1次碰撞发生.

小球不与弹簧发生第n+1次作用的条件分为两种情形：

1)第n次作用后，小球不能冲上斜面，应满足条件：

(6)

2)小球冲上斜面，之后再滑下斜面时小球速度向左，应满足条件：

(7)

由式(6)、式(7)可得

(8)

由式(5)、式(8)可得，小球只与弹簧发生n次作用条件为

(9)

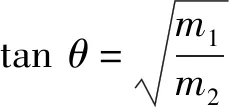
(10)

根据上文小球不与弹簧发生第n+1次作用有两种情形.若第n次作用后，小球不能冲上斜面，则速度矢量与竖直负半轴夹角为θ+(n-1)2θ，速度矢量为

(11)

(12)

3 结语