基于参数跟踪的感应电机转速与磁链强跟踪滤波估计方法

张中磊 ，薄婷婷 ，孙传杰 ，王自满 ，姜一达 ，杨敬然 ，田凯

（1.天津电气科学研究院有限公司，天津 300180；2.电气传动国家工程研究中心，天津 300180；3.国网天津市电力公司检修公司，天津 300250）

感应电机以其适应性强、运行可靠等优点，在高性能传动控制领域得到越来越广泛的应用。磁场定向矢量控制可以实现感应电机的转矩与磁链解耦，具有优越的动态控制性能，是目前应用最广泛的控制方法[1]。在感应电机的矢量控制系统中，转速与磁链的闭环控制是实现磁场准确定向和高性能控制的关键，尤其在无速度传感器控制中，不仅要求其具有较高的转速控制精度、较快的动态响应，而且还需要具有较强的模型鲁棒性[2-3]。随着高性能矢量控制要求的不断提高和无速度传感器容错控制技术的发展，如何快速准确地获取感应电机的转速和磁链信息以及提高转速估计精度和磁链观测性能，显得极为重要。许多学者对感应电机参数辨识和状态估计问题开展了大量研究，主要方法集中在改进电压-电流模型[4]、模型参考自适应[5-6]、自适应状态观测器[7-8]、扩展卡尔曼滤波器[9-11]以及人工智能[12-13]等方法。改进电压-电流模型方法在一定程度上克服了电压模型法和电流模型法的缺点，但对电机参数的鲁棒性差，属于开环系统，并且两种模型在切换过程中存在抖动。模型参考自适应方法过度依赖参考模型的准确性，电机参数的变化影响状态估计精度和控制效果，而对电机参数进行在线辨识将大大增加控制器负荷和自适应律设计难度。自适应状态观测器受电机参数变化和噪声干扰的影响较小，但磁链观测的不确定性会导致转速自适应律在全速范围内不能满足正实性，并且受电机状态方程固有极点的限制和反馈增益矩阵设计的影响，低速发电状态的转速估计性能不如高速场合，可能会出现观测器不稳定的现象[14-15]。扩展卡尔曼滤波（extended Kalman filter，EKF）算法可以有效对非线性系统进行状态估计，并且能够削弱测量噪声及随机干扰的影响，但EKF算法对电机模型不确定性和参数变化的鲁棒性较差，尤其对突变状态的跟踪可能引起不稳定[16]。

为改善感应电机由于参数变化及模型不确定性引起的转速与磁链估计性能差，尤其是对突变状态不能快速准确跟踪和低速运行时的估计精度低的问题，本文提出一种包含粒子群优化（particle swarm optimization，PSO）迭代学习参数跟踪的强跟踪滤波（strong tracking filter，STF）估计方法，针对电机参数变化及模型不确定性，采用PSO迭代学习动态优化算法实现对电机参数的在线跟踪，修正的STF算法用于实现对感应电机转速与转子磁链的高性能联合估计。与现有的自适应观测器和扩展卡尔曼滤波方法相比，包含参数跟踪的STF方法利用粒子群优化算法对电机参数进行辨识，改善因参数变化引起的模型误差，并通过引入时变渐消因子，在线调整卡尔曼增益矩阵，使残差序列保持正交，迫使STF保持对系统状态的准确跟踪[17]，提高估计精度与对突变状态的跟踪能力。最后通过仿真对比，验证了包含参数跟踪的STF算法在状态估计精度、跟踪速度和稳定性方面的优越性。

1 感应电机数学模型

忽略感应电机的磁路非线性及铁损等影响，选择定子电流、转子磁链及电机转速作为状态变量，得到两相静止坐标系下离散化状态方程为

雅克比矩阵如下式：

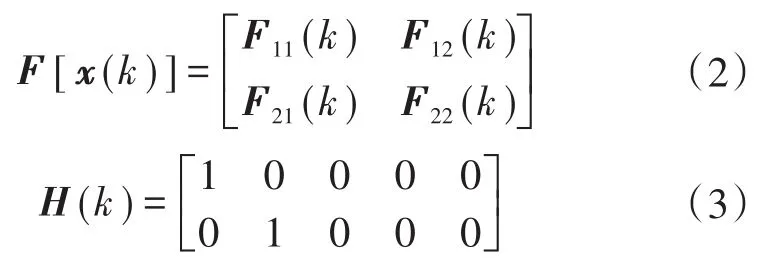
2 包含参数跟踪的强跟踪滤波方法

2.1 包含时变渐消因子的强跟踪滤波器

考虑非线性时变离散状态空间模型：

其中，过程激励噪声w和测量噪声v均为不相关的零均值高斯白噪声，其协方差矩阵Q和R分别为对称非负定矩阵和对称正定矩阵。

具有时变渐消因子的STF递推算法为如下：

步骤 1：设置初始值 x̂(0|0)，P(0|0)以及噪声协方差矩阵 Q(k)，R(k)。

步骤2：状态预测与输出预测如下式：

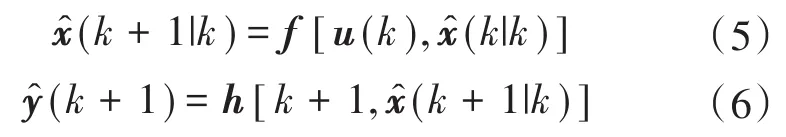
步骤3：计算输出残差：

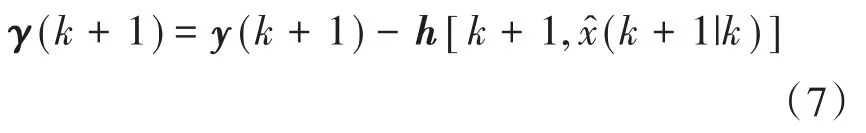
步骤4：计算残差协方差矩阵：

式中：ρ为遗忘因子，取值在0～1之间。

步骤5：计算时变次优渐消因子：

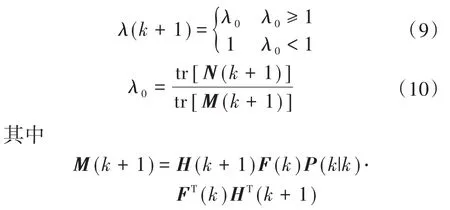
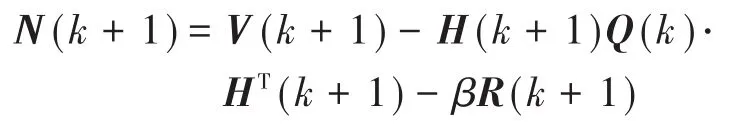
式中：β为弱化因子，用于削弱渐消因子的调节，使状态估计更加平滑；tr[]为矩阵求迹运算；λ(k+1)为时变渐消因子；M(k+1)，N(k+1)为计算渐消因子过程中的中间变量。

步骤6：状态误差协方差预测：

式中：LMD为多重次优渐消因子。

步骤7：计算卡尔曼增益矩阵：

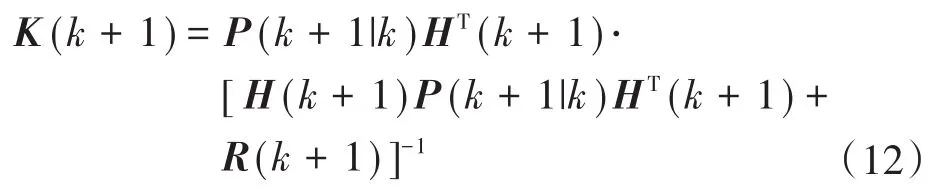
步骤8：更新状态误差协方差：

步骤9：状态校正如下：

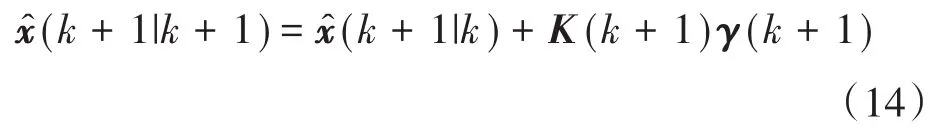
当模型不确定性和状态突变造成滤波器的状态估计偏离系统的实际状态时，必然会在输出残差序列上表现出来。STF算法利用时变渐消因子对过去数据进行渐消，并实时调整状态误差协方差阵的预测值以及相应的增益阵，使残差序列满足下式所示的正交性，迫使强跟踪滤波器保持对系统实际状态的准确跟踪。

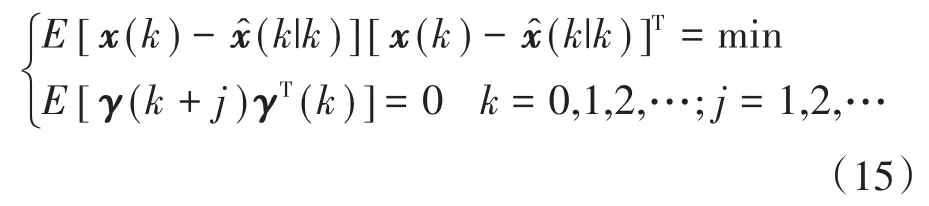
2.2 基于PSO迭代学习动态优化算法的参数跟踪

PSO迭代学习动态优化算法是一类基于群智能的随机全局优化进化算法，该算法以其实现容易、精度高、收敛速度快和适应性强等优点得到广泛应用[18]。在PSO算法中，种群中的每个粒子代表寻优空间中的一个潜在解，适应值由被优化的函数决定，粒子群通过个体间的协作竞争与学习进化，实现多维空间中最优解的搜索。在每次迭代进化中，粒子通过自身和群体的历史最优位置，更新当前的速度和位置。在任意k+1时刻，第i个粒子的速度和位置更新公式为

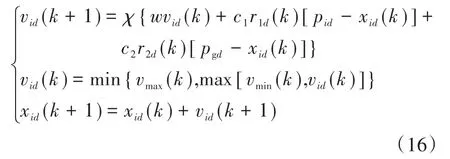
式中：d为解空间的维数；i为种群规模，i=1,2,…,N；vid，xid分别为第 i个粒子的速度和位置；χ为限制因子；w为惯性权重因子；c1为认知加速因子，所在项表征粒子自身的学习进化；c2为社会加速因子，所在项表征粒子之间的信息共享与合作；pid，pgd分别为个体和群体的历史最优位置；r1d，r2d为两个相互独立的服从[0，1]均匀分布的随机数。

该粒子所经历的历史最后位置的函数值为pbesti，粒子群所经历的历史最优位置对应的函数值为gbest。

设置最大迭代次数为itermax，当前迭代次数为iter，惯性权重w随迭代次数线性下降：

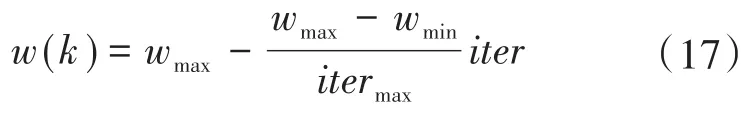
限制因子χ取：

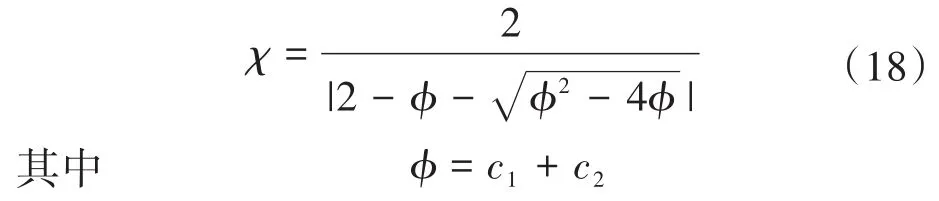
构建适应度函数为

其中，罚因子γ表示适应度函数中转速分量与定子电流分量的权重。

PSO迭代学习动态优化算法通过构造与被控对象具有相似结构的可调感应电机模型，计算辨识模型与参考系统的输出残差，通过适应度函数进行评价，利用适应度评价值对可调模型中待辨识参数进行修正，不断重复迭代学习过程，直到模型输出的性能指标达到最优或者到达最大迭代次数，从而实现对感应电机的参数跟踪。

3 仿真结果

为验证包含参数跟踪的STF状态估计算法的有效性，构建如图1所示的感应电机矢量控制系统，并进行系统仿真。其中，PSO参数跟踪部分用于对感应电机定子参数与转动惯量进行跟踪，STF状态估计部分用于对感应电机的转速与转子磁链进行联合估计，参数跟踪辨识出的电机参数值用于修正STF算法中的系数矩阵。设置定子电阻Rs=1.54 Ω，定子电感Ls=0.100 4 H，转子电阻Rr=1.294 Ω，转子电感 Lr=0.096 9 H，励磁电感Lm=0.091 5 H，转动惯量J=0.15 kg·m²。

图1 包含参数跟踪STF算法的感应电机矢量控制系统Fig.1 FOC system of induction motor with parameter tracking and STF

考虑感应电机的转动惯量与定子参数变化及模型不确定性，构造与电机动态模型相同结构的被辨识模型，以被控模型和辨识模型的输出残差加权平方和的积分作为优化指标，采用PSO迭代学习动态优化算法对感应电机定子电阻Rs、定子电感Ls及转动惯量J进行在线跟踪。PSO算法设置种群规模为N=50，最大迭代次数为itermax=200，惯性权重系数 wmax=0.9，wmin=0.4，加速因子c1=c2=2.05，限制因子χ =0.73，罚因子γ =0.2。在迭代次数为iter=50时，转动惯量J突变为初始值的1.2倍，定子电阻Rs突变为初始值的1.25倍，定子电感Ls突变为初始值的1.2倍。

图2为PSO迭代学习动态优化算法结束时粒子群分布与最优适应度函数值gbest。图3为迭代优化得到的感应电机转动惯量J、定子电阻Rs与定子电感Ls以及包含扰动的参数跟踪波形。从图中可以看出，PSO迭代学习动态优化算法具有较好的参数跟踪性能和较高的稳态精度。

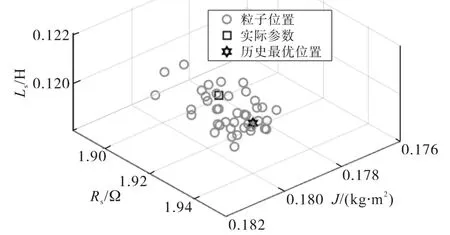
图2 PSO迭代优化结果与粒子群分布Fig.2 PSO iterative optimization results and particle swarm distribution

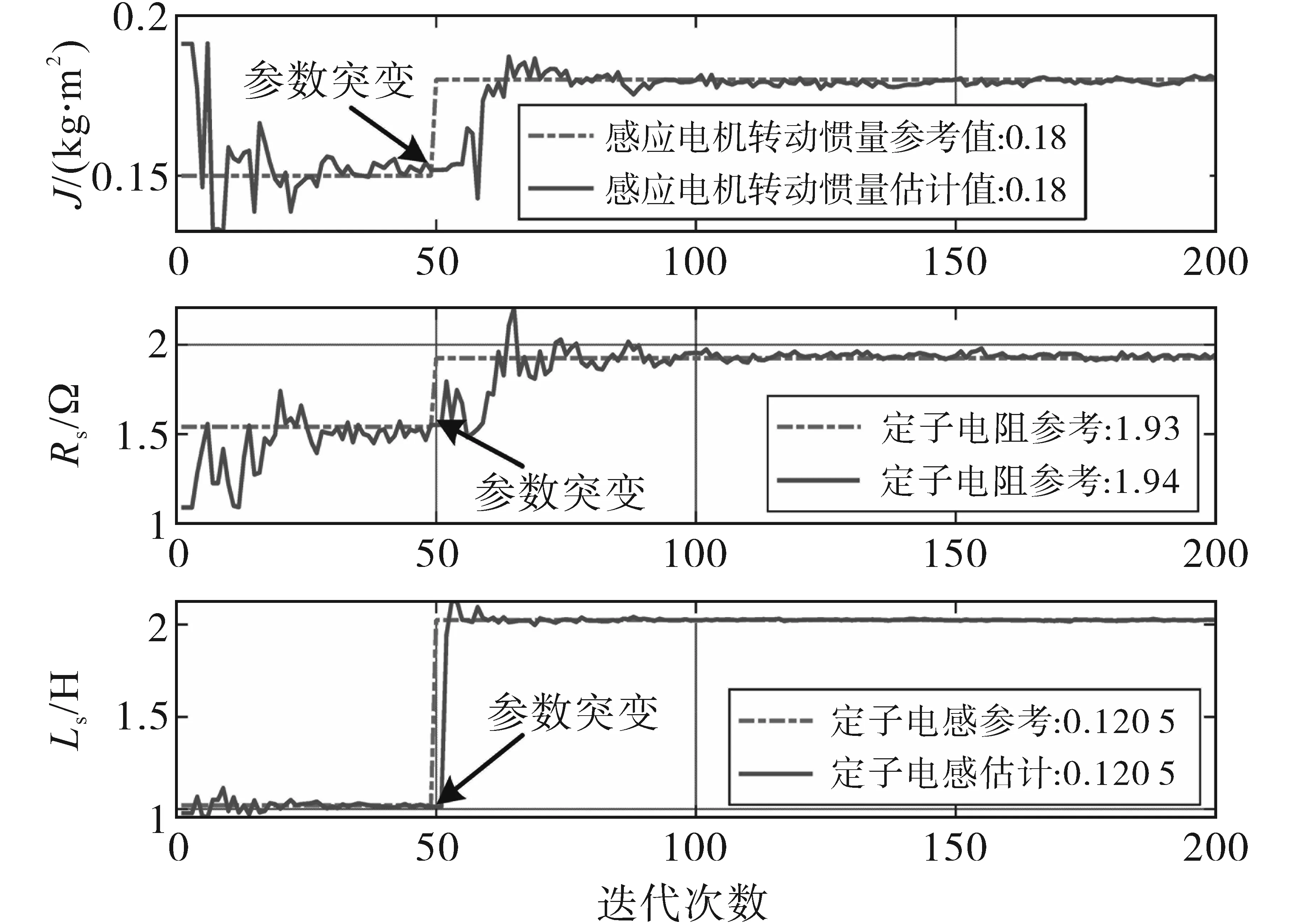
图3 感应电机参数PSO辨识结果Fig.3 Results of parameters identification of IM with PSO

在STF状态估计部分，采用时变次优渐消因子对滤波算法中的过去数据渐消，实时调整状态预测误差协方差阵及Kalman滤波增益阵，实现对状态的精确实时估计。系统初始误差协方差阵P(0|0)、噪声协方差阵Q和R的取值影响STF的估计性能，Q取值过小会对突变状态的跟踪存在滞后，Q取值过大会导致稳态精度和抗扰能力下降。综合考虑算法的动态性能、收敛速度及稳定性，本文中取初始P(0|0)=diag(10-6I4,10-4I1)，Q=diag(2×10-6I4,5×10-5I1)，R=3×10-2I2，遗忘因子ρ=0.95，弱化因子β=1.2。仿真初始给定转速为2 rad/s，在2 s时阶跃增至80 rad/s，在仿真时间 2～6 s内，转速为80 rad/s；在6 s时阶跃降至50 rad/s。为验证STF算法的鲁棒性，仿真中设置随机干扰噪声及测量噪声，以及负载扰动，STF对包含随机噪声负载转矩的估计结果如图4所示。

图4 随机扰动负载转矩及STF估计结果Fig.4 Results of load torque STF estimation with stochastic disturbance

电机转速与转子磁链的STF估计结果如下：图5为感应电机转速估计仿真波形，可以看出，EKF和STF两种估计算法均具有较好的估计性能，并对电机参数变化具有较强的鲁棒性。将其中极低速段、中速段以及过渡段的转速估计波形放大，如图6～图8所示，STF算法具有更高的转速估计精度和对突变状态的跟踪能力，尤其在低速段的跟踪能力与估计精度明显优于EKF算法，并对负载扰动具有较强的鲁棒性。图9为定子电压、定子电流波形，可以看出，转速过渡段的电压、电流切换较为平滑，定子电流的STF估计精度较好。

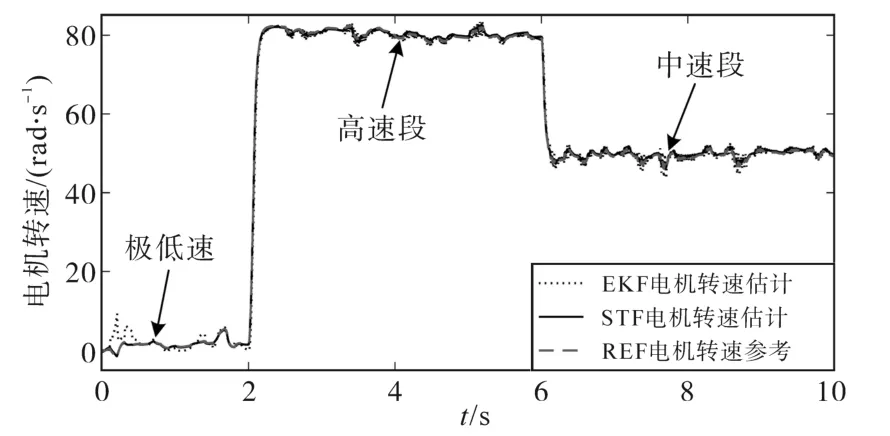
图5 全速域内转速估计仿真结果Fig.5 Simulation results of speed estimation at all-speeds

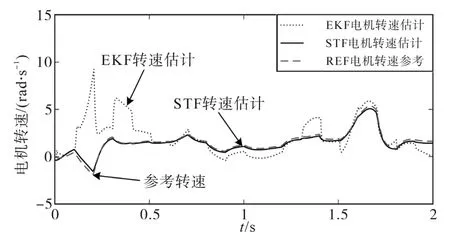
图6 极低速段转速估计结果Fig.6 Results of speed estimation at very-low speed

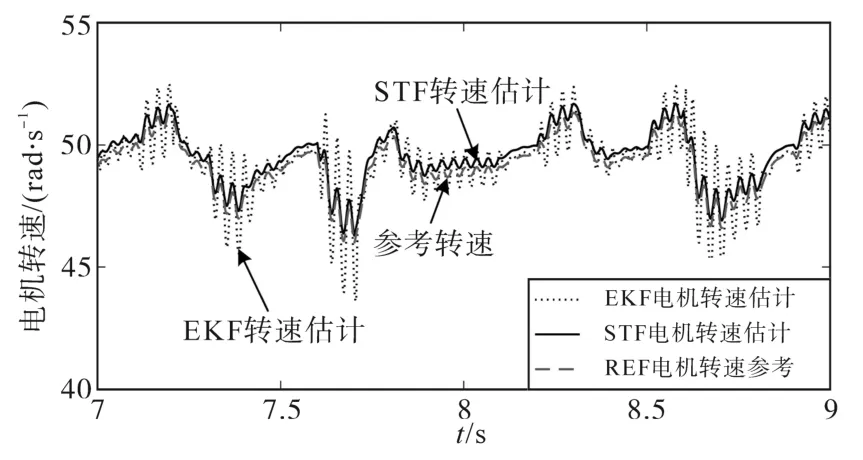
图7 中速段转速估计结果Fig.7 Results of speed estimation at medium speed

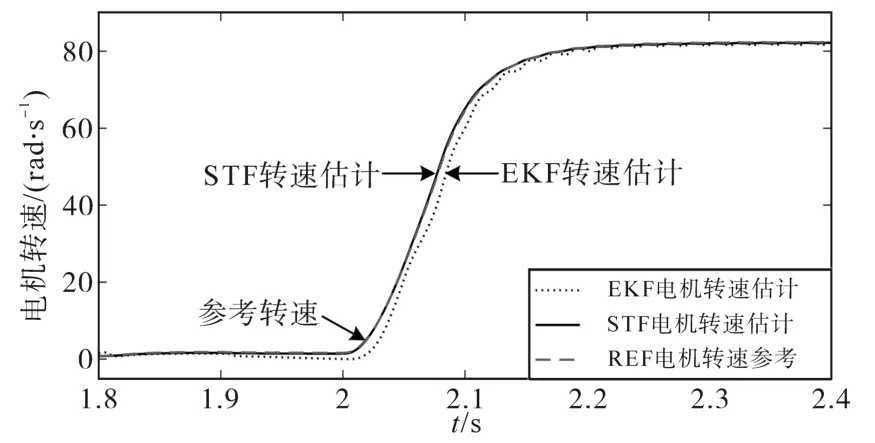
图8 转速阶跃过渡段转速估计结果Fig.8 Results of speed estimation with speed step

图9 定子电压与定子电流波形Fig.9 Waveforms of stator voltages and stator currents

图10为感应电机转子磁链估计仿真波形，可见，EKF与STF两种估计算法在中、高转速段的估计效果较好，在低速段的转子磁链估计误差较大。图11～图13分别是在极低速段、中速段以及转速过渡段的转子磁链估计放大波形。在极低转速段，STF与EKF的估计精度较差，但STF算法能够快速跟踪参考磁链波形，动态性能优于EKF。在高速段与中速段，STF与EKF均具有较高的稳态估计精度，相对参考磁链稳态误差在2%以内。在转速阶跃过渡段，EKF算法对突变状态的跟踪不稳定，而STF算法能够快速跟踪磁链，并具有较好的动态性能和跟踪精度。

图10 全速域内转子磁链估计仿真结果Fig.10 Simulation results of rotor flux estimation at all-speeds

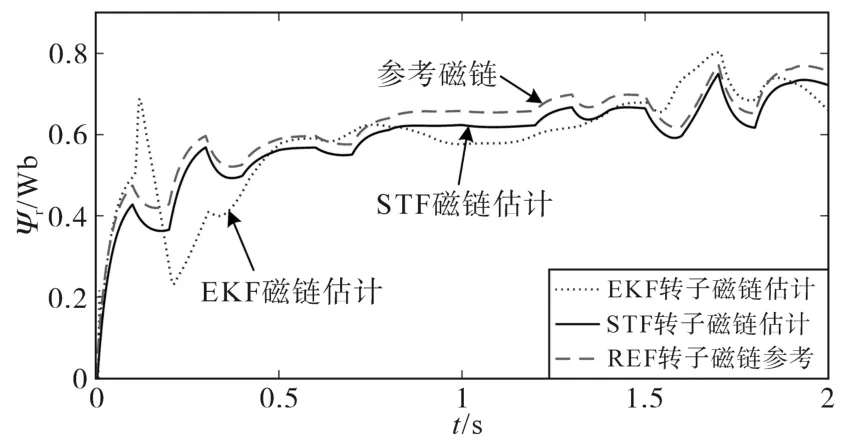
图11 极低速段转子磁链估计结果Fig.11 Results of rotor flux estimation at very-low speed

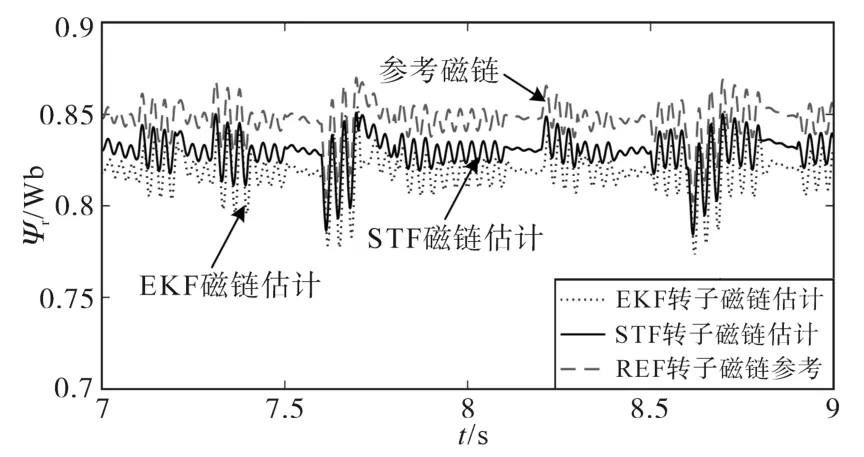
图12 中速段转子磁链估计结果Fig.12 Results of rotor flux estimation at medium speed

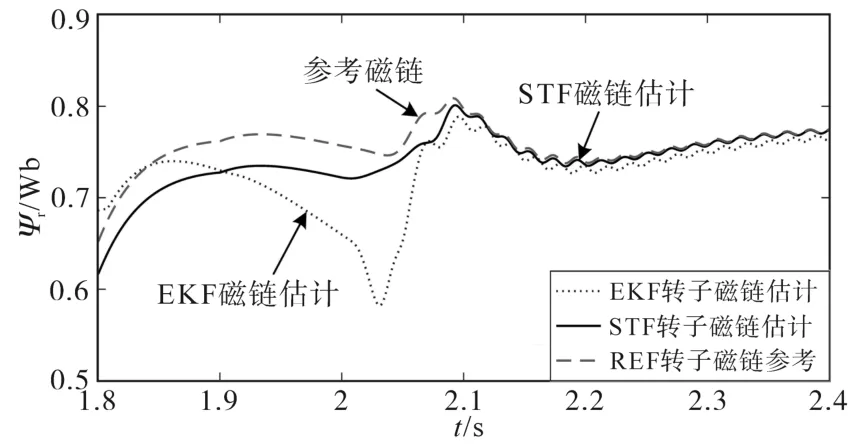
图13 转速阶跃过渡段转子磁链估计结果Fig.13 Results of rotor flux estimation with speed step

4 结论

本文提出了包含参数跟踪的感应电机转速与磁链联合估计的STF方法，针对电机参数变化及模型不确定性，采用PSO迭代学习动态优化算法实现对电机参数的在线跟踪，修正的STF算法用于实现对感应电机状态的联合估计。仿真结果表明，STF能够有效实现对感应电机转速与转子磁链的高性能估计。与EKF相比，包含参数跟踪的STF算法在估计精度、跟踪速度和稳定性方面均得到大幅度改善，并且能够快速跟踪突变状态，尤其在低速段仍能保持较好的估计性能，有效提高了状态估计精度和算法鲁棒性。