±800 kV直流特高压T型塔埃菲尔效应特性研究

2021-06-09潘峰金益迥梅宇佳潘羽黄静文

广东电力 2021年5期

潘峰，金益迥，梅宇佳，潘羽，黄静文

(1.中国能源建设集团浙江省电力设计院有限公司，浙江杭州 310012；2.国网浙江省电力有限公司台州供电公司，浙江台州 318000)

输电铁塔上的荷载作用主要包含风荷载(导地线和塔身)、导地线张力和导地线及铁塔自身重力荷载。对于悬垂塔，导地线风荷载和塔身风荷载控制了许多构件(尤其是斜材)的规格选取。风荷载由平均风荷载和脉动风荷载组成，铁塔上某处的风速随着高度的增加而增大，并随时间脉动发生变化。对于风荷载的随机性，一般认为在同一高度的塔身某处，不大可能同时达到风速最大的情况。对坡度单一铁塔的主、斜材，风的随机性对内力基本没有影响，但当铁塔主材坡度成曲线状或多折线状时，脉动风荷载对斜材内力的影响明显加强[1]。鉴于曲线状或多折线状铁塔与法国埃菲尔铁塔的外形相似，因此这种效应称为斜材的“埃菲尔效应”。

国内外关于铁塔埃菲尔效应的研究相对较少。唐国安[2]以某500 kV拉线猫头塔倒塔事故为例，研究了埃菲尔效应的特性，提出应对建议，认为BS 8100英国规范[3]规定的主导思想是可以接受的，但在物理概念方面含混不清，有待改进。南俊[4]对钢塔的埃菲尔效应进行了研究，通过风荷载模拟和时程分析，对大量铁塔进行了分析计算，得出铁塔塔身斜材内力静力计算和时程分析的差别，并提出避免埃菲尔效应的措施。王子龙[5]根据我国高耸结构设计规范的计算公式和输电塔塔身几何关系进行推导，得到埃菲尔效应的计算公式，可直接应用于输电塔计算软件TTA的结果文件中。郭夏阳[6]结合某500 kV双同路直线塔，对塔身斜材的埃菲尔效应进行计算和对比分析，得出采用折减系数法设计计算是偏于安全的结论，建议塔身斜材内力一般可取主材内力的3%考虑。王文明[7]采用内力比法、折减系数法和剪力比方法对某大跨越塔进行分析，研究埃菲尔效应对杆塔斜材内力的影响，建议大跨越杆塔设计时采用剪力比法。韩军科[8]对比分析国内外塔桅结构埃菲尔效应计算方法，得出结论：为满足铁塔埃菲尔效应，斜材设计内力不小于主材内力的3%，否则对于对超、特高压交流同塔多回路输电铁塔而言，可能偏于不安全。

对于埃菲尔效应的分析，国外许多设计规范也给出了相应的计算方法，例如BS 8100英国规范[3]、BS EN 1993-3-1[9]欧洲规范和TIA-222-G[10]美国规范等，国外规范对于铁塔设计埃菲尔效应的计算各有特点。我国高耸结构设计规范[11]和架空输电线路杆塔结构设计规定[12]也给出了埃菲尔效应的计算方法。

本文旨在对±800 kV直流特高压T型塔的埃菲尔效应进行细致研究，为埃菲尔效应在±800 kV特高压直流输电线路工程中的应用提供参考依据。

1 埃菲尔效应原理

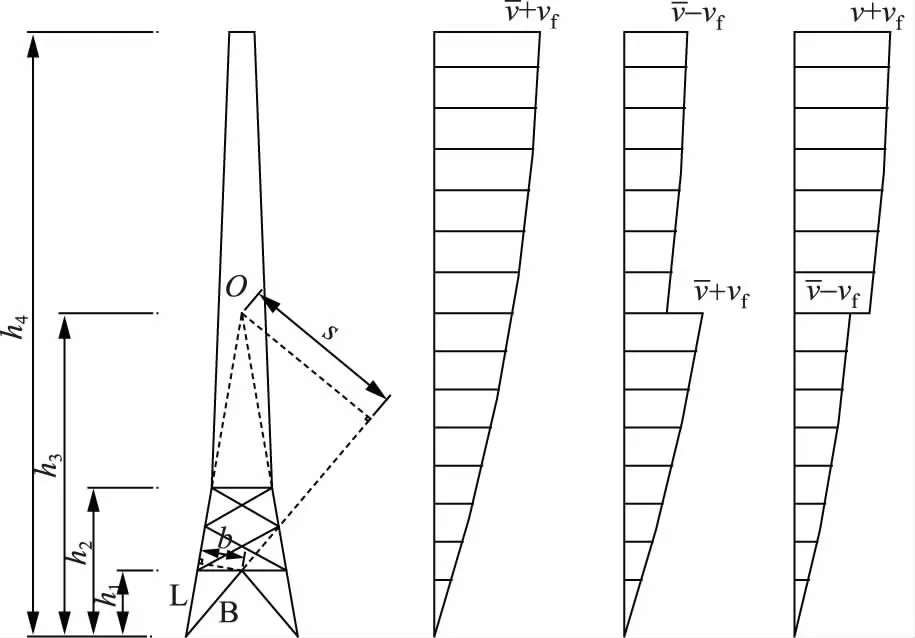
图1 埃菲尔效应计算示意图Fig.1 Calculation diagram of Eiffel effect

根据力学平衡原理，主材L的内力

(1)

式中：z为离地高度；q(z)为z高度处的风压值；μsz为z高度的铁塔体型系数；Az为z高度构件的风压投影面积；B为风荷载覆冰增大系数。斜材B的内力

(2)

根据式(1)和式(2)可知主材与斜材内力计算有明显差别。像铁塔这样的三维桁架结构，斜材内力大小取决于交点O上下的弯矩，主要有以下3种情况：①当数值大于0时，斜材承受拉力，反之承受压力；②当数值的绝对值达到最大时，斜材承受最大拉力或最大压力；③当数值等于0时，交点O上下两部分塔身风荷载对O点的弯矩等于0，此时斜材内力也等于0。

由此可以得出结论：脉动风在铁塔上的分布与斜材内力大小密切相关。当铁塔下部主材交点O位于塔顶以下时，在交点O上下将产生相反的弯矩作用，随着时间变化，弯矩差值也在不断变化，当超过一定范围时，斜材内力也会随之发生较大变化；因此，必须校核可能的最不利情况，得出最大的斜材内力，保证结构安全。

埃菲尔效应原理的另一种解释是：当四边形铁塔平行边方向受风荷载时，取一侧主材斜度较大的一层进行受力分析，如图2所示。图2中：M、V为塔截面受到的弯矩和剪力，θ为主材坡度夹角，w为塔截面宽度。

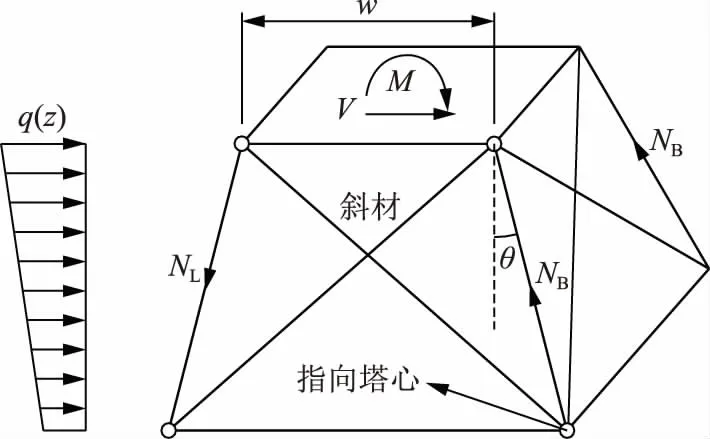
图2 埃菲尔效应原理Fig.2 Schematic diagram of Eiffel effect principle

假设斜材为虚杆，其受力忽略不计，则主材的平衡条件如下：

(3)

∑X=0,(NL+NB)sinθ=Q.

(4)

式(3)、(4)中：Q为该层所承受的总剪力；MO和X分别表示总弯矩和总水平力。

由式(3)和式(4)得

(5)

则式(5)即为出现埃菲尔效应的条件。令

(6)

当Q/Qm-1≈0时，静力计算得到的斜材内力与实际风荷载作用下的斜材内力存在较大的差别；用下标m表示某一层剪力。

设Δ=|Q/Qm-1|，则出现埃菲尔效应的条件变为Δ=0，Δ值即等于|(Q-Qm)/Qm|，其中Qm为主材分担的剪力，|Q-Qm|为斜材所承担的剪力，所以Δ为斜材与主材所承受的剪力比。埃菲尔效应的结果与Δ值有直接关联：Δ值越小，斜材剪力越小，埃菲尔效应越显著，反之，埃菲尔效应越弱。

2 埃菲尔效应的计算方法

参考国内外的设计规范，BS 8100英国规范、BS EN 1993-3-1欧洲规范、TIA-222-G美国规范和中国高耸结构设计规范和杆塔设计规定提出了埃菲尔效应相应的计算方法，这些规范推荐的计算方法各有特点。

2.1 BS 8100英国规范方法

BS 8100英国规范是铁塔设计最早考虑斜材埃菲尔效应的经典规范，首先利用平均风荷载得到铁塔的主材和斜材内力，然后分别乘以不同的阵风响应系数G，得到主材和斜材内力。即

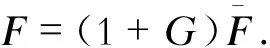
(7)

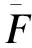
(8)

斜材内力的阵风响应系数

(9)

式(8)、(9)中：Gb为基本阵风响应系数，可根据地形、高度获得；zm、zq分别为主材、斜材的离地高度；H为铁塔总高度；Kq为与1/|fq|相对应的系数，fq为平均风速下zq高度处斜材承担的剪力与总剪力之比的绝对值，当1/|fq|>8时，

(10)

对比式(7)和式(8)，斜材内力计算比主材内力计算增加了响应系数Kq，根据条文说明，Kq为斜材埃菲尔效应的增大系数。Kq的数值与地面粗糙度、剪力比fq、斜材在塔上的位置高度(H-zq)有关。当塔高300 m、fq为0.125～1.000、地形类别为Ⅰ—Ⅴ、Kq值为1.0～3.2时，斜材内力增幅较为明显；当fq<0.125时，Kq可按式(10)计算得到，曲线如图3所示。

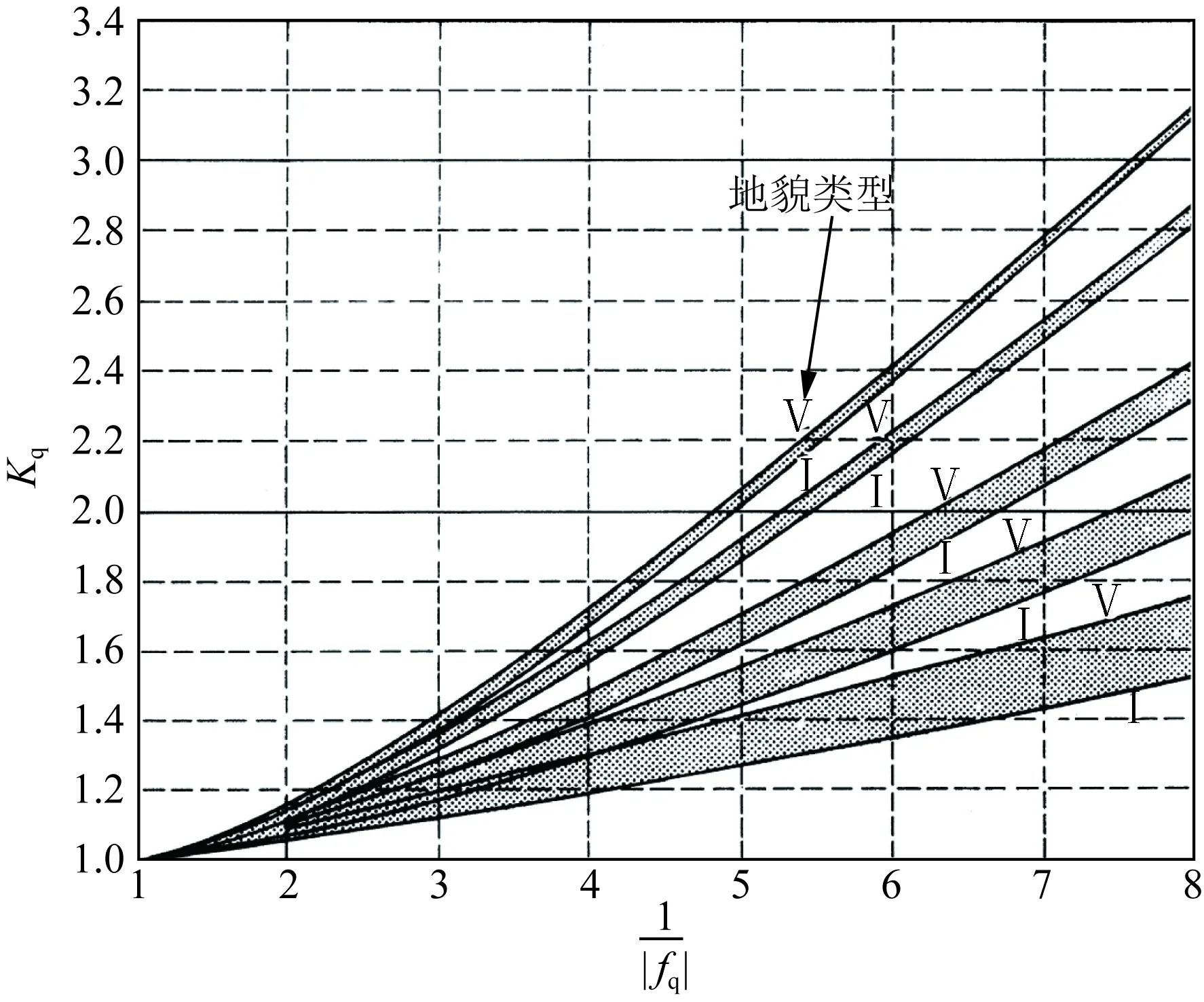
图3 Kq曲线示意图Fig.3 Schematic diagram of Kq

2.2 BS EN 1993-3-1欧洲规范方法

欧洲规范中斜材内力的计算方法引入剪力缀补荷载的设计概念，与BS 8100有所不同。图4给出了计算斜材内力的几种缀补荷载的情况。主要有以下2种工况：①对于两坡度铁塔，当A段主材的交点在塔顶以上，斜材内力可按图4中工况1(按全塔作用阵风响应荷载)计算；当A段主材坡度的交点位于塔顶以下时，斜材的内力参考图4中工况2(按交点上下作用平均荷载和阵风荷载的组合)计算。②对于三坡度铁塔，应分析每个坡度段主材交点的具体位置。当主材交点位于塔顶以下，该坡度段的斜材应按相应的风荷载组合计算确定斜材内力。图4中编号1—8表示8种风荷载计算模式。采用欧洲规范，可利用铁塔内力分析程序计直接得到斜材设计内力，方法相对简单。

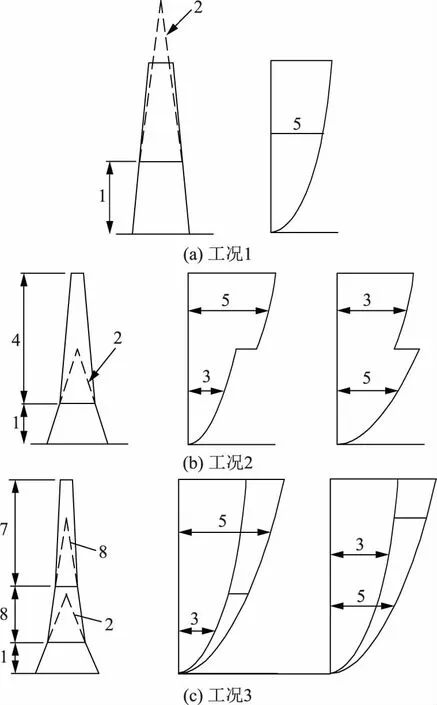
图4 欧洲规范计算示意图Fig.4 Calculation diagram of European codes for Eiffel effect

2.3 TIA-222-G美国规范方法

美国规范也采用缀补荷载法计算铁塔的斜材内力，计算原则与欧洲规范方法基本一致，不同点主要在主材交点上下的荷载取值。

图5为美国规范给出的计算构件内力的缀补荷载计算示意图，主要有以下3种情况：①主材交点位于塔顶以上，构件内力按全高梯度风荷载计算；②主材交点位于塔身内，构件内力应按1—3的风荷载工况组合计算；③塔身两段主材的交点都位于塔身内，构件内力应按1—5的风荷载工况组合计算。当塔身主材为多坡度时，可按上述计算原则增加相应的风荷载工况组合计算。

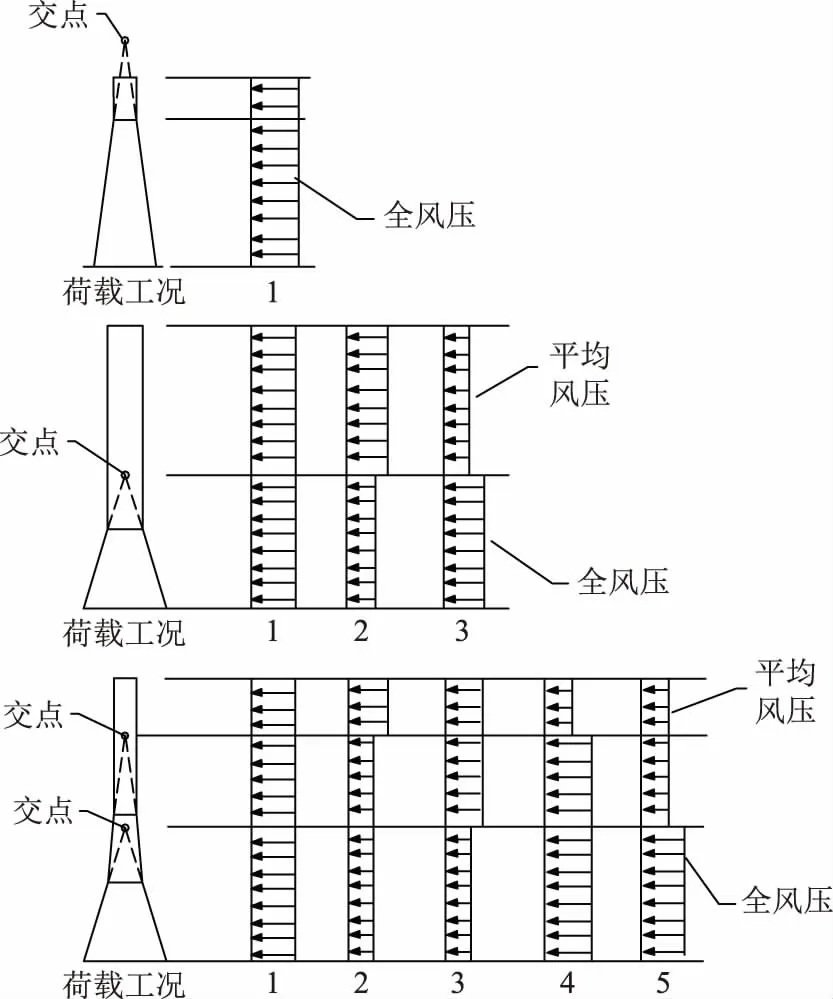
图5 美国TIA规范计算示意图Fig.5 Calculation diagram of US TIA code for Eiffel effect

对于图5，满风荷载

Fst=qzGhSEPS.

(11)

式中：qz为已考虑高度效应的风压值；Gh为阵风响应系数；SEPS为有效受风面积，包含构件体型系数、构件投影面积。平均风荷载等于满风荷载乘以转换系数，不同地貌类别下的转换系数见表1。

表1 平均风荷载折减系数取值Tab.1 The average wind load reduction factor

2.4 中国高耸结构设计规范方法

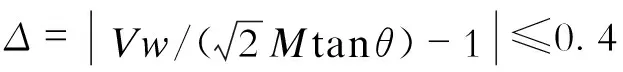
(12)

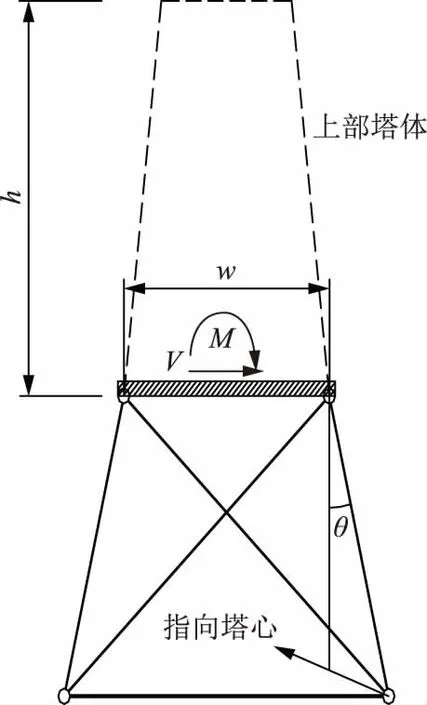
图6 我国高耸结构设计规范斜材计算示意图Fig.6 Calculation diagram of China’s high-rising code for Eiffel effect

式中：h为所计算截面以上塔体高度；μ为系数，刚性斜材取1.0，柔性斜材取2.0。

2.5 中国架空输电线路杆塔设计规定方法

按照DL/T 5154—2012的规定，杆塔斜材的埃菲尔效应可采取折减系数法和剪力比法进行计算[12-13]。

折减系数法的设计风荷载是指按设计基本风速和相关系数计算确定的水平风荷载，折减风荷载是将设计风荷载乘以折减系数后得到的风荷载。折减荷载法主要适用于90°大风或0°大风的情况，计算步骤如下：①确定主材交点位置；②将杆塔分成上下两部分；③上下分别作用设计风荷载和折减风荷载，组成不同荷载工况；④与其他工况合并计算，求得最大斜材内力。图7所示为折减法荷载工况。

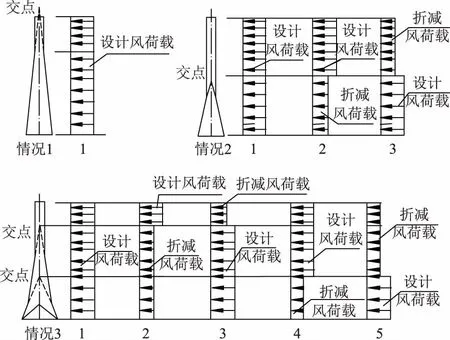
图7 折减法荷载工况示意图Fig.7 Calculation diagram of load case for reduction factor method

如图7所示：情况1，变坡段主材交点位于塔顶以上，仅需按设计风荷载计算即可；情况2，变坡段主材交点位于塔身内，杆塔上下两部分应按图示3个荷载工况计算；情况3，塔身有3个坡度段，主材的2个交点都位于塔身内，应按图示5个荷载工况计算。当杆塔主材具有更多坡段，按上述方法类推。表2为折减系数的取值。

表2 折减系数法中折减系数取值Tab.2 Reduction factor values in the reduction factor method

DL/T 5154—2012同时规定：若曲线形铁塔斜材没有按照折减系数法或剪力比法考虑埃菲尔效应，为保证斜材具有足够的承载能力，其设计内力不宜小于相应主材内力的3%。

3 直流塔埃菲尔效应计算

以±800 kV直流特高压T型塔ZP30102作为研究对象，图8所示为ZP30102塔主材坡度示意图。采用谐波合成法(WAWS)模拟节点的风荷载，通过时程分析，得到构件拉压内力。其中，段3主材坡度按0.10、0.12、0.14、0.16、0.20分别计算铁塔的风致振动响应值，得到主、斜材的内力，同时进行相应的内力统计分析。

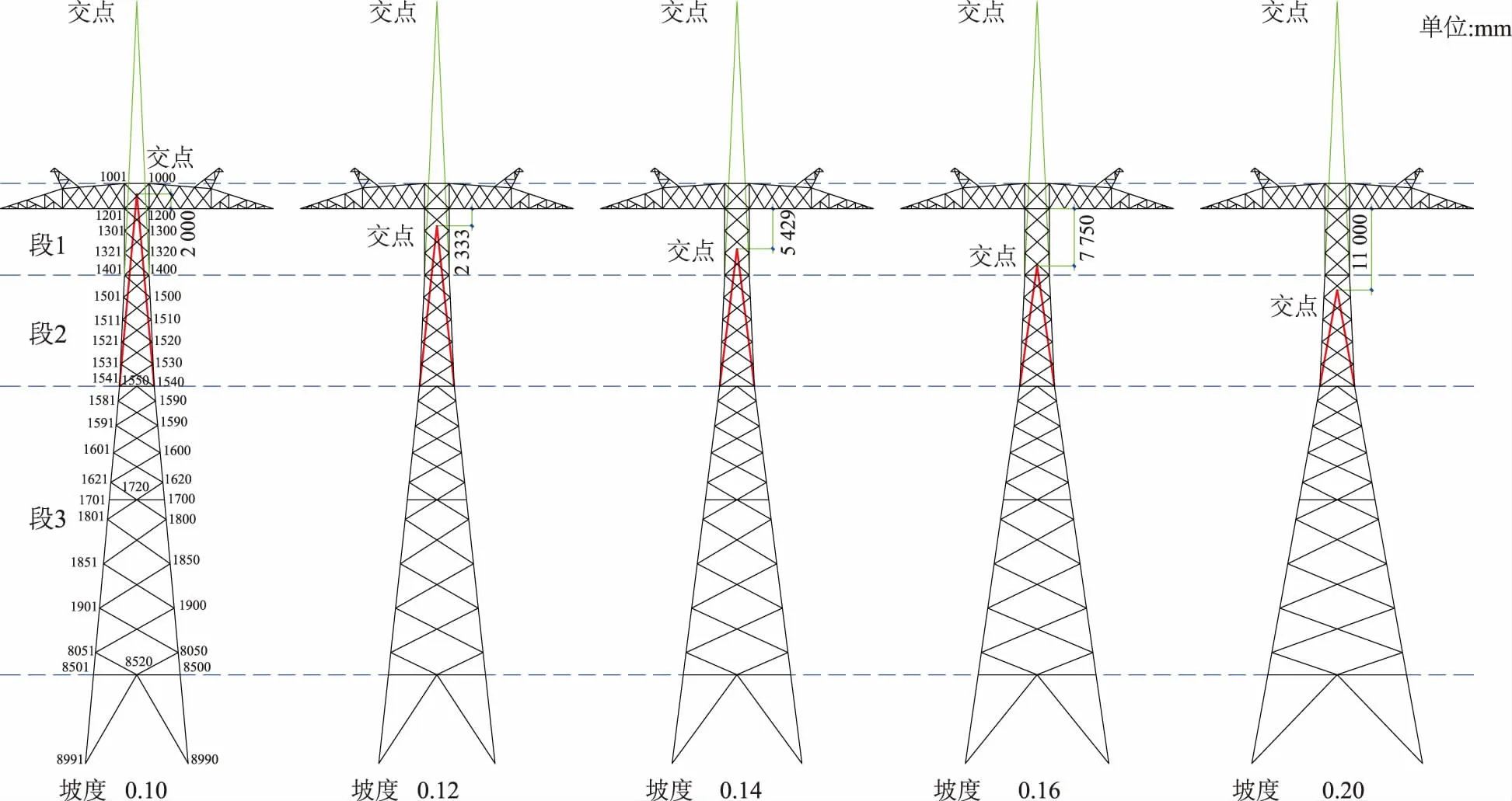
图8 直流塔ZP30102主材变坡示意图Fig.8 Schematic diagram of different slopes of DC tower ZP30102 principal material

图9所示为不同坡度情况下段3斜材节点1600-1622的内力变化示意图。

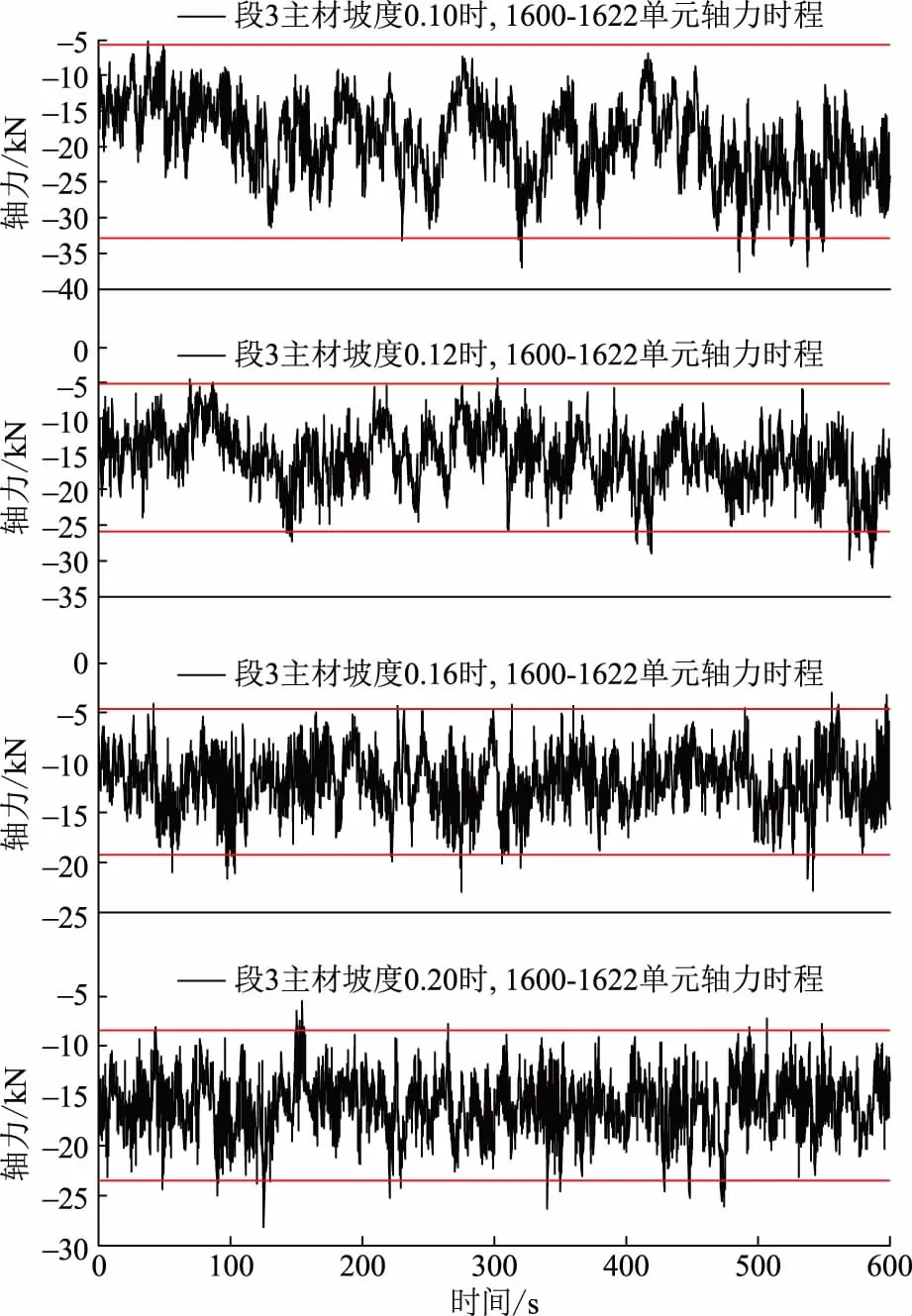
图9 不同坡度斜材1600-1622内力变化示意图Fig.9 Schematic diagram of internal force variation of different slopes for 1600-1622

由图9可知，随着坡度变化，段3斜材内力变化不显著。表3—表5分别为段3主材坡度为0.12、0.16和0.20时斜材内力比较；表6为不同折减系数(3∶7或2∶8)取值的斜材内力比较。

从表3—表6可知：

a) 由于段1和段2(段3变坡以上)的主材交点处于塔顶部上，折减系数法和铁塔通用程序计算得到的段1、段2之间的斜材内力基本一致，说明埃菲尔效应不显著；由于计算时风振系数已按工程经验进行取值，横担的取值相对较大，而时程法按实际风荷载计算，故得到的斜材内力最小；根据时程法计算结论，铁塔横担的风振系数的取值可适当减小。

b) 段3主材坡度0.10为最终的设计坡度，铁塔通用程序、折减系数法和时程法计算得到的斜材与主材内力之比基本接近，斜材内力也较为接近，时程法的结果比另外2种方法计算得到的结果稍大，从段3变坡处开始往塔底方向的斜材与主材内力之比逐渐增大，比值逐渐超过3%。由于段3主材交点处于塔身内外交界处，埃菲尔效应并不显著，可直接采用铁塔通用程序进行计算。

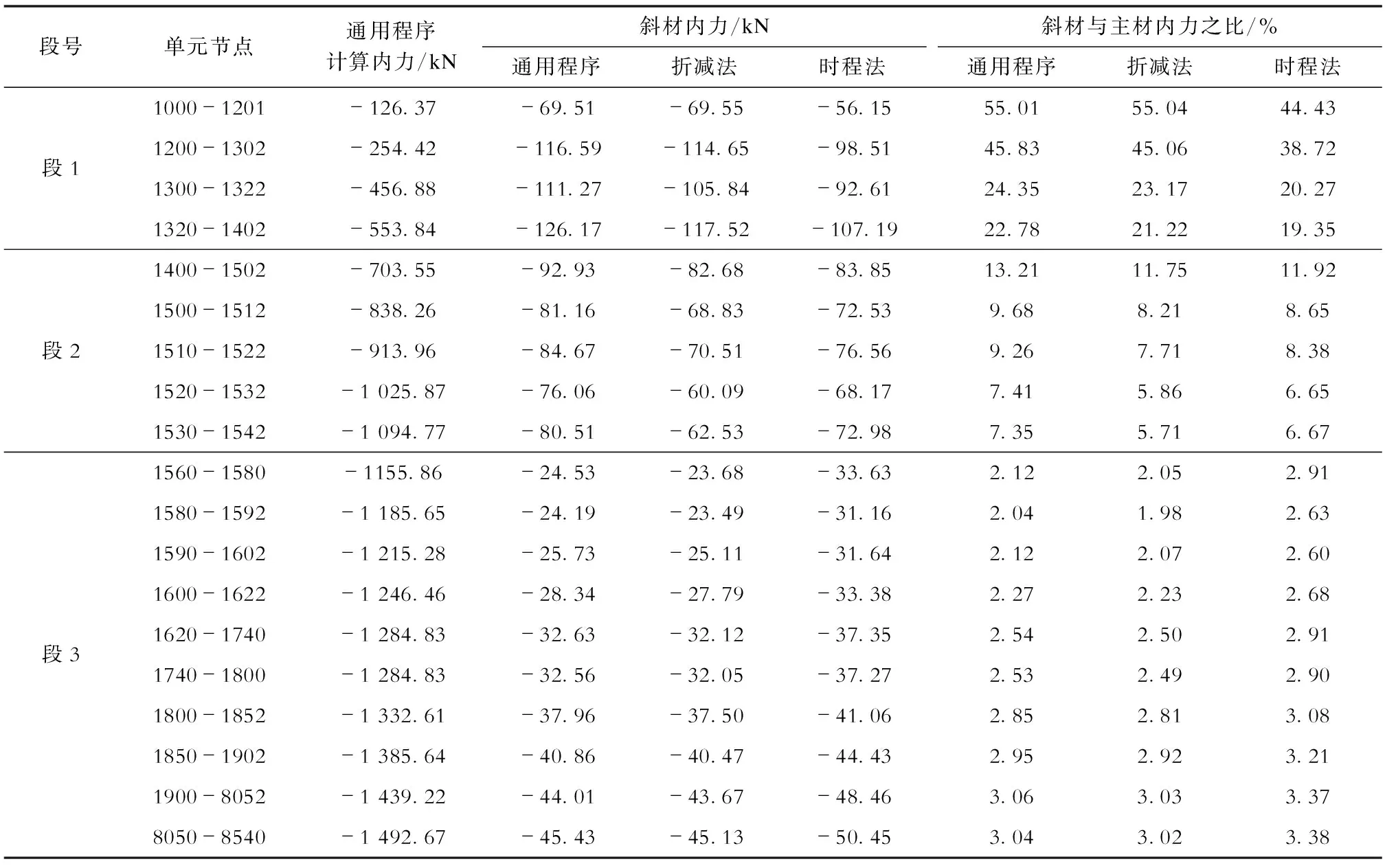
表3 段3主材坡度为0.10时斜材内力比较Tab.3 Internal force comparisons when the slope of the principal material of section 3 is 0.10

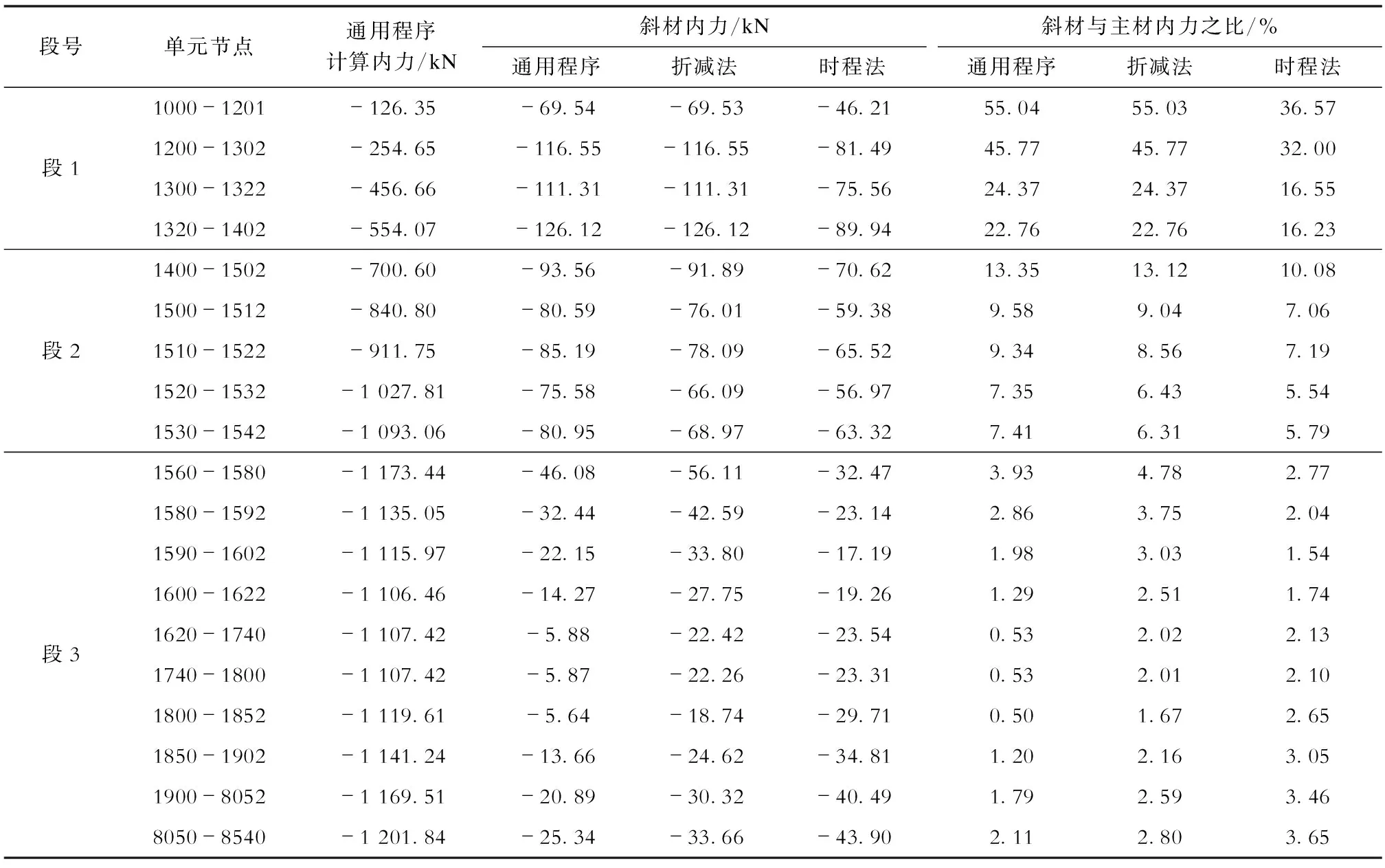
表4 段3主材坡度为0.16时斜材内力比较Tab.4 Internal force comparisons when the slope of the principal material of section 3 is 0.16

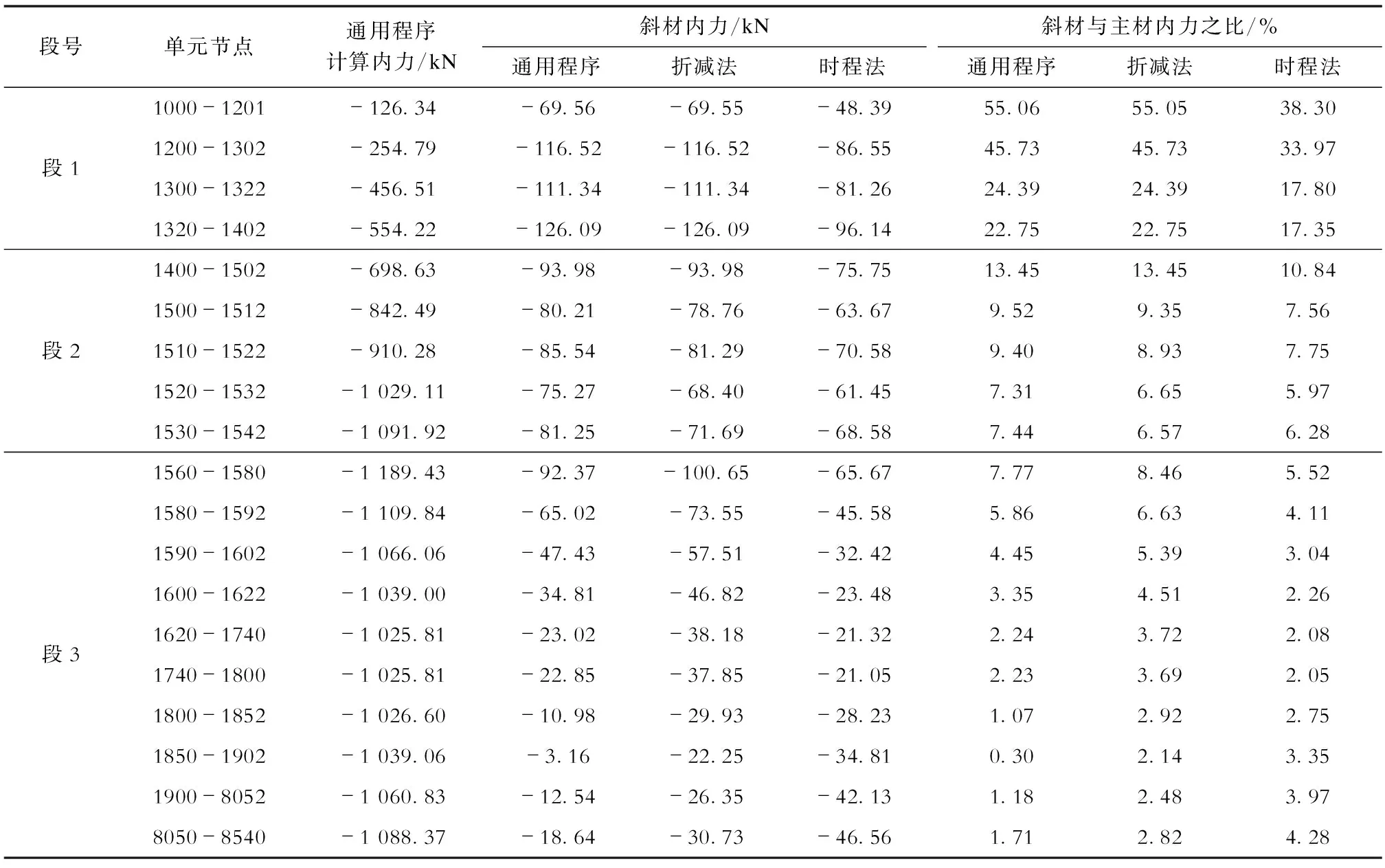
表5 段3主材坡度为0.20时斜材内力比较Tab.5 Internal force comparisons when the slope of the principal material of section 3 is 0.20

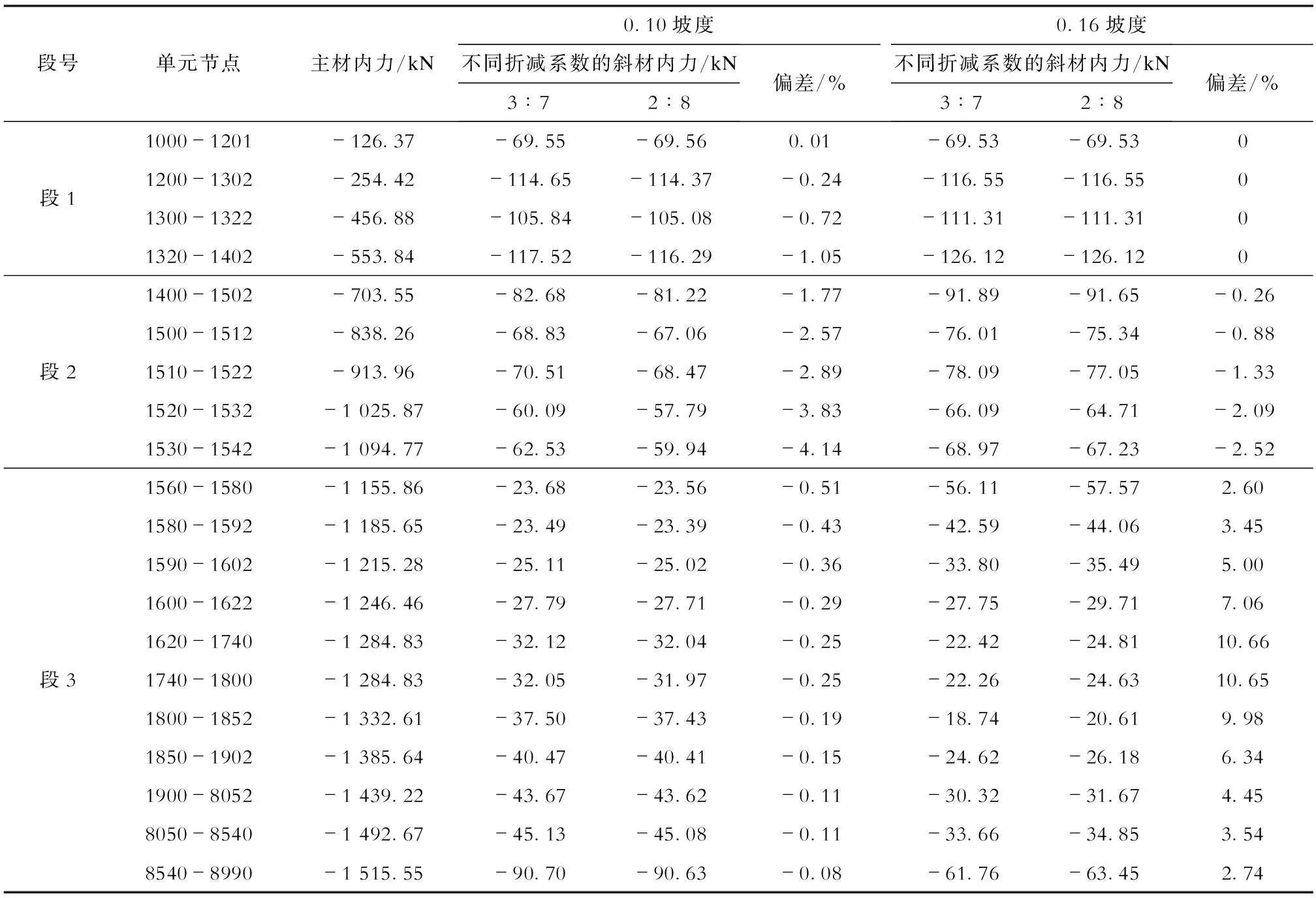
表6 段3不同折减系数时斜材内力比较Tab.6 Internal force comparisons with different reduction factors

c) 随着段3主材坡度从0.12到0.20变化，斜材内力的埃菲尔效应逐渐明显，铁塔通用程序计算的结果明显小于折减系数法和时程法计算的结果，部分斜材内力由铁塔通用程序计算明显小于主材内力3%，而折减法和时程法计算结果则已接近主材内力的3%或超过3%；折减法计算结果与时程法基本相当，但时程法计算过程较为复杂，折减系数法相对简单，其计算结果可以作为设计参考。

d)随着不同折减系数(3∶7和2∶8)取值变化，当主材坡度不大时，不同折减系数取值斜材内力的大小基本一致；当主材坡度增大时，2∶8折减系数时的斜材内力逐步增大，增幅在3%～10%之间，斜材内力的埃菲尔效应逐渐明显。

e)DL/T 5154—2012规定斜材设计内力不宜小于主材内力的3%是合理的；对于没有进行埃菲尔效应计算的±800 kV直流输电塔，建议按照不小于主材内力4%来校核，以保证结构安全。