智能配电网监测系统的无损数据压缩方案
2021-06-09陈赟王宇雷
陈赟,王宇雷
(1.中国葛洲坝集团电力有限责任公司,湖北 武汉 430034;2.强电磁工程与新技术国家重点实验室 (华中科技大学),湖北 武汉 430074;3.华中科技大学 电气与电子工程学院,湖北 武汉 430074)
智能配电网设备众多,接线复杂,伴随着智能电网概念的提出和大数据概念的推广应用,智能配电网监测系统需要实现更多更精细的功能。与之对应,在智能配电网的监测系统中需要传输海量的监测数据。因此,无论是从提高智能配电网监测系统实时性能的角度看,还是从减少数据传输系统的建设与运行维护成本考虑,研究适用于智能配电网监测系统的数据压缩方案都具有重要的实际意义与经济价值[1]。
传统的电力系统数据处理方法——离散傅里叶变换(discrete Fourier transform,DFT)及其快速算法——快速傅里叶变换(fast Fourier transform,FFT)可以视为对采样值数据的一种压缩方法,相对于工频每周波80、200、256乃至更多个点的采样值数据,经DFT/FFT得到的幅值、频率及相角数据要少很多。近几十年来,随着小波变换的提出与推广[2],离散小波变换(discrete wavelet transform,DWT)在电力系统数据压缩领域中的应用也得到了充分的研究。文献[3-12]对DWT在电力领域中的应用进行了研究。文献[3]将DWT应用于船舶电力监控系统中,通过与旋转门算法共同作用,有效减少了船舶电力监控系统中的数据量。文献[4]将整数小波变换与LZ77算法相结合,在整数小波变换后,通过对低频分量采用LZ77算法进行无损压缩,对高频分量采用阈值量化进行有损压缩,由此取得了较高的数据压缩比率和较低的数据重构误差。文献[5]采用二维提升格式整数小波变换,充分利用了电能质量数据周期性和对称性的特点,在确保数据准确性的前提下提高了数据的压缩比。文献[6]采用双树复小波变换,对包括电压暂升、暂降、闪烁以及谐波等在内的多种信号进行了压缩,取得了良好的压缩效果。文献[7]也利用电能质量数据的周期性,与文献[5]不同的是,文献[7]不对电能质量数据直接进行DWT,而是先令输入信号与参考信号进行减法计算,通过对差值进行DWT,以实现对电能质量数据的压缩。文献[8]对小波包的子树分解进行研究,提出一种最优子树的选取方法。文献[9-10]对DWT系数的编码方法进行研究分析,其中:文献[9]将嵌入式零树编码应用到电力录波中;文献[10]则通过频谱形状估计对熵编码进行优化。文献[11]结合DCT方法与DWT方法,并在DCT与DWT之前使用主成分分析技术对PMU数据进行预处理。文献[12]研究小波压缩在电厂设备中的应用,不再将DWT方法局限于电压电流信号的采样值数据,扩展了小波压缩的应用范围。2006年,一种新的数据处理方法——压缩感知(compressed sensing,CS)理论被提出[13-14],被迅速应用于电力系统的数据压缩领域中[15-17]。文献[15]对当前国内外CS方法在电力系统中的应用做了详尽的综述。文献[16]将CS方法应用于电能质量数据的压缩中。文献[17]则更近一步,结合分布式CS和边缘计算技术对电能质量的数据进行压缩。文献[18-19]分别将分形插值方法与奇异值分解方法应用于智能电网的数据压缩中,也取得较好的效果。
到目前为止,上述几种方法尚存在着应用范围较窄(集中于采样值数据)、实时性较差(需要加时间窗)等问题。其中:DFT/FFT与DWT应用于数据压缩领域时,压缩过程相对复杂,耗时较长;相对于研究比较充分的DFT/FFT与DWT,CS方法应用于电力系统数据压缩时性能较差。另一方面,尽管理论上DFT/FFT与DWT、CS都可以实现无损数据压缩,但在实际应用中,采用上述方法直接进行无损数据压缩的压缩性能都比较差,这主要源自于上述方法中存在的固有缺陷。由于在实际应用中存在大量不同步采样,DFT/FFT会受到栅栏效应的影响。如果数据采样不是同步采样,DFT/FFT还会受到频谱泄漏效应的影响;如果采样频率不足,DFT/FFT还会受到频谱混叠效应的影响。当前CS在电力系统中的应用研究基于DFT稀疏基,因此上述3种效应同样会对基于CS方法的数据压缩方案产生影响。而从稀疏理论的角度来看,对于大多数电力系统信号(采样值数据),DFT稀疏基优于小波稀疏基,这意味着DFT方法在理论上的性能要优于DWT方法。
由于无损数据压缩以及应用在智能配电网数据传输方面的研究较少,本文针对智能配电网的监测数据,提出一种综合性的无损数据压缩方案,并对该方案进行模拟仿真,验证其有效性。
1 数据压缩方案的设计方法
图1为将数据压缩方案应用于数据传输的通用流程,包含数据压缩、数据传输与数据解压缩3个过程。通常,可将数据解压缩过程视作数据压缩过程的逆过程,即在设计好数据压缩过程后,可通过对数据压缩过程进行逆向解析设计得到数据解压缩过程。
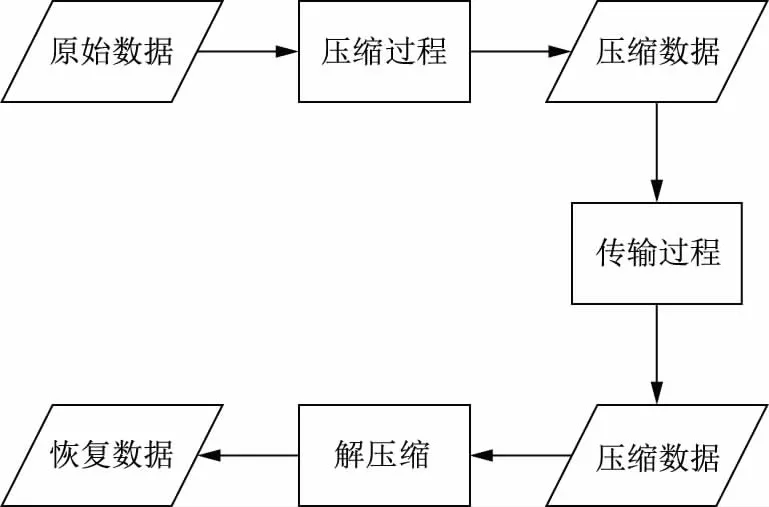
图1 数据压缩应用于数据传输的通用流程Fig.1 General process of data compression applying to data transmission
一套完整的数据压缩方案通常由多个不同的数据压缩方法有机组合构成,按照原始数据与恢复数据是否完全一致可将数据压缩方法分为无损压缩方法和有损压缩方法两类。对于无损数据压缩方法,香农第一定理(Shannon first coding theory)指出,任何数据模型均有一个理论上的最小编码率,如式(1)所示:
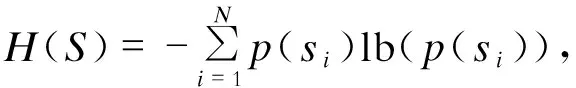
si∈S,i=1,2,…,N.
(1)
式中:S为数据模型,该数据模型中含有N个元素,si为其中第i个元素,这里,数据模型是对实例对象抽象特征的提取与符号描述;p(si)为第i个元素在S中出现的概率;H(S)被称为香农熵,为数据模型S的最小编码率。
香农第一定理指出对于任何一组数据实例,其无损压缩性能都有一个理论上的极限值。理论上的最小编码率是十分难以达到的,但是其对于设计无损压缩方法的指导意义却是十分明确的,即数据模型的可压缩性与数据模型的概率模型直接相关。其中,数据模型的概率模型指的是数据模型中每个元素出现的概率的集合。针对一组特定的数据,首先建立合适的数据模型,然后通过统计或其他手段为数据模型建立精确或近似的概率模型,再基于概率模型为数据模型设计新的编码模型,并用新的编码模型取代原始的编码模型对数据进行编码以实现无损数据压缩,这就是设计无损压缩方法的一般方法。这里,数据模型的编码模型指的是数据模型中每个元素所对应的编码符号的集合。
典型的无损数据压缩方法如霍夫曼编码就体现了这种设计思想。常规的编码模型会为数据模型中的每一个元素分配相同位长的编码符号;而在霍夫曼编码中,则会选择为出现概率较大的元素分配一个位长较短的编码符号,为出现概率较小的元素分配一个位长较长的编码符号。定义压缩比
(2)
式中:So为原始数据;Sc为压缩数据。
2 基于预测的无损压缩方案
2.1 方案的总体框架
在智能配电网的监测系统中,存在着各种各样的数据,每种数据有其独特的特征与数据模型,对应不同形式的概率模型;因此,一般来说,难以直接为智能配电网监测系统的各种数据设计一种通用形式的编码模型。
但智能配电网是一个实际的物理系统,而物理系统一个显著的特征即是其在时间与空间上的连续性。智能配电网监测系统所监测的大部分信号(除少数情况,如电感电压、电容电流等)在时间与空间上都是连续的,信号在前一时刻与后一时刻的幅值、频率、相角等各种表征数据是接近的,相近地点的相同类型的信号的幅值、频率、相角等表征数据也是接近的。基于智能配电网监测系统信号的这一特征,本文提出一种基于预测的无损数据压缩方案,该方案为智能配电网的数据压缩提供一种统一的处理方式(要求被压缩数据满足前述连续性要求),其总体框架如图2所示。
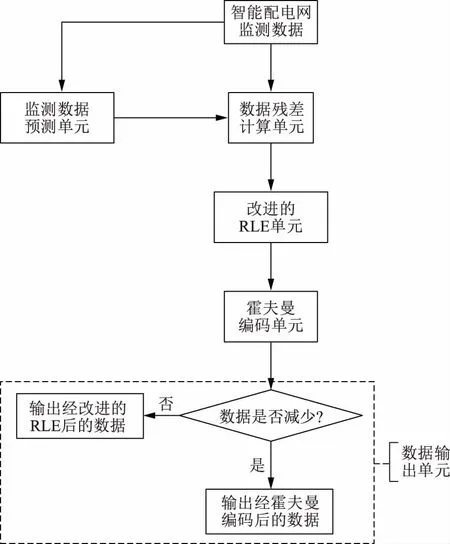
RLE—行程编码,run length encoding的缩写。
如图2所示,该无损压缩方案由数据残差计算单元、监测数据预测单元、改进的RLE单元、霍夫曼编码单元与数据输出单元组成。其中,数据残差计算单元计算智能配电网监测数据当前值与预测值之间的差值;监测数据预测单元对当前监测数据的取值进行预测,以使数据残差尽可能小;改进的RLE单元与霍夫曼编码单元执行对数据的编码压缩;由于经RLE后的数据经霍夫曼编码算法再编码后不一定得到压缩,数据输出单元会对此执行一个比较判断,只有当霍夫曼编码算法确实对RLE后数据起到压缩作用时,才会输出霍夫曼编码后的数据,否则输出RLE后的数据。
2.2 监测数据预测单元
如前所述,监测数据预测单元对当前监测数据的取值进行预测,以使数据残差尽可能小,预测精度的高低会直接影响最终的数据压缩效果。然而,信号数据取值的精确预测是十分困难的,通常需要结合信号的多个特征进行,这样不仅会大大提高本文所提无损数据压缩方案的复杂度,也会使适用面大大缩小。鉴于以上原因,本文基于智能配电网监测信号时间上的连续性对信号的取值进行预测。
一种最为简单也是适用面最广的预测方法是直接采用监测信号采样数据的上一个取值作为参考监测数据(本文将这种方法称之为前值预测法),但是采用这种预测方法得到的监测数据的预测值精度较低,仅适合某些压缩比要求较低或者连续但不可导的监测数据。为此,本文将信号在时间上的连续性要求加强为信号在时间上具备多阶可导性,对于智能配电网的多数监测信号,这一要求可近似满足。
利用泰勒公式可以对在时域上多阶可导的信号进行预测,如式(3)所示,所采用的阶数越多,预测越精确,残差越小。
(3)
式中:f(x)为一个n阶可导的连续函数;f(n)(x0)为其在x0点的n阶导数;Rn(x)为余项,即残差。
基于综合考虑(计算复杂度与对信号多阶可导性的要求),本文采用2阶泰勒公式对信号进行预测(此时要求监测信号2阶可导):
λdn-1.
(4)
式中:s′n为信号在时刻tn的预测值;sn为信号在时刻tn的值;dn为信号在时刻tn的残差;λ为加权参数,0≤λ≤1。式(4)的最后一项用以模拟泰勒公式中的余项Rn(x)。
当被压缩的配电网监测数据采用等间隔方法采样时,式(4)可以被简化为
s′n=2.5sn-1-2sn-2+0.5sn-3+λdn-1.
(5)
由式(4)、(5)可知,相对于前值预测法,基于2阶泰勒公式的预测法利用了更多的历史监测数据,对监测信号在时间上的连续性利用更充分。当式(5)中λ=0.5或λ=0.25时,式(5)的计算可以由加法器完成,而不需要乘法器的参与,此时,监测数据预测单元的计算十分简单,计算快速且易于实现。
另外,数据压缩端和数据解压缩端皆需要进行监测数据的预测,压缩端由实际数据和预测数据计算残差数据,解压缩端由残差数据和预测数据恢复实际数据。
2.3 数据残差计算单元
数据残差计算单元首先计算当前监测数据的残差
dn=sn-s′n.
(6)
此时残差数据仍采用原始数据的编码模型,对应原始数据的概率模型,然而残差数据的数据模型/概率模型与原始数据的数据模型/概率模型并不相同,原始数据的编码模型对于残差数据冗余,残差数据能够通过设计适用于残差数据的编码模型来压缩。
假设原始数据的取值范围(即峰峰值)映射到了取值区间的上下限(即编码符号的每一位都被实际使用),经过残差计算,残差数据的取值范围大幅减小,对应于概率模型,即在原始数据模型中大部分幅值较大的元素,现在其出现概率变为0,或者出现概率变得极其小,而幅值较小的元素的出现概率则大幅提升。如前文中举例所提到的霍夫曼编码方法,对于出现概率为0的元素,可以不对其进行编码,对于出现概率较小的元素,可以为其分配一个位长较长的编码符号,对于出现概率较大的元素,可以为其分配一个位长较短的编码符号,由此实现数据的压缩。
为了进一步提高编码效率,在进行霍夫曼编码之前,先对残差数据进行RLE以获得更高的压缩性能。注意到经过残差计算,智能配电网的监测数据不仅没有被压缩,反而为每个数据增加了一个符号位。另一方面,由于预测不可能完全精确,残差数据将在一定范围(0值附近)内反复波动。这一结果致使对残差数据直接进行RLE时,效率会十分低下,因为尽管残差数据的重复概率大幅提升,但是残差数据并没有表现出连续重复的特性,而RLE要求数据连续重复。因此,需要对残差数据进行处理以将残差数据的重复性增强为连续重复性。
对残差数据的处理方法源自于图像的位平面编码方法,如图3、图4所示。图3中,每行代表1个数据,共有16个数据(16行),每个数据占用2个字节,加上1个符号位,一共17位。
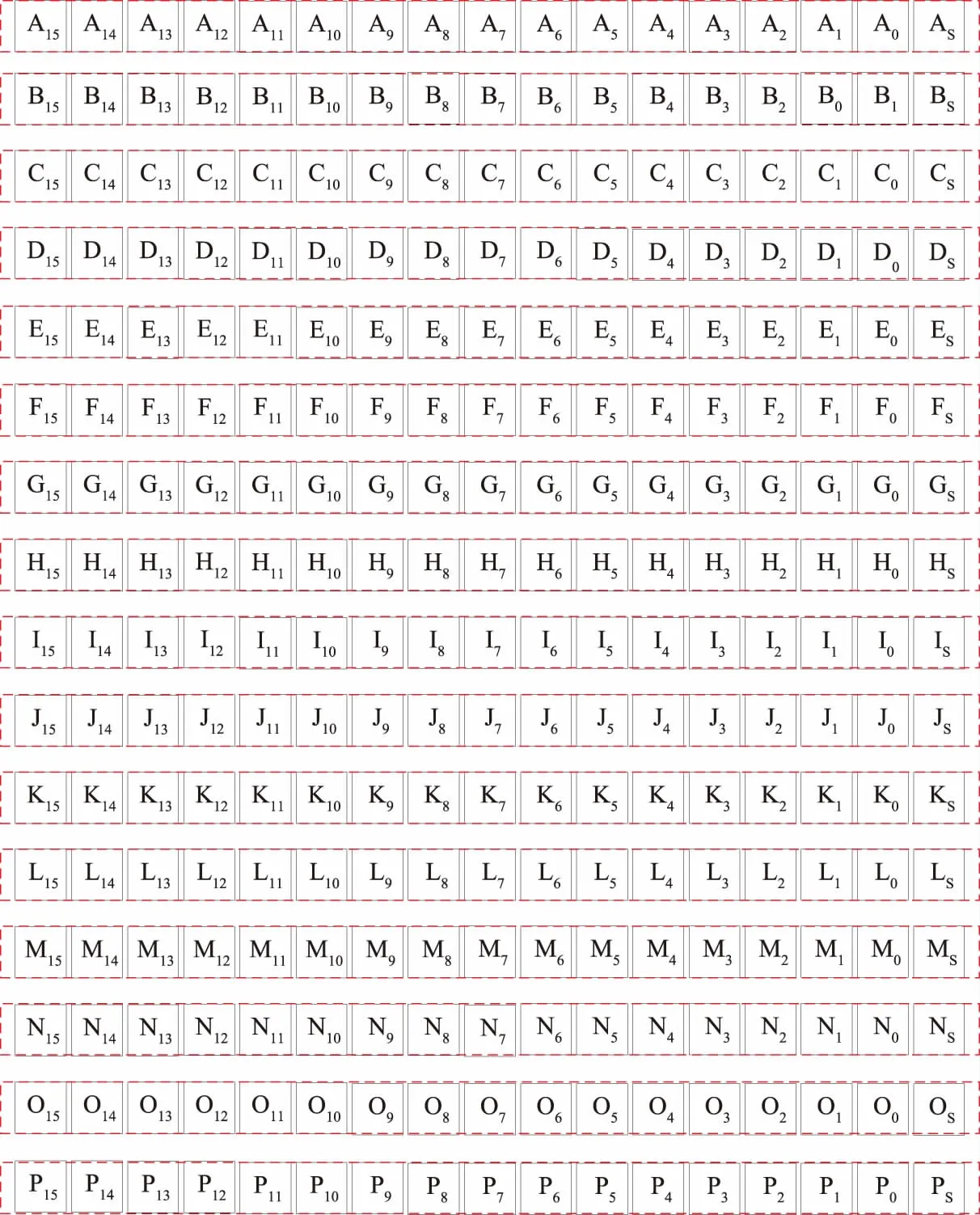
图3 原始数据的二进制排列方式Fig.3 Binary arrangement of original data
对图3中的数据进行重排序(类似于矩阵中的转置操作),得到图4中的数据。在图4中,按照从左到右、从上到下的顺序,每8位视为1个新数据,合计34个数据。可以发现,图4中的每行的数据皆来自于原始数据的对应的各个位,如图4中第1行的2个数据由原始各个数据的第15位按顺序排列而成。
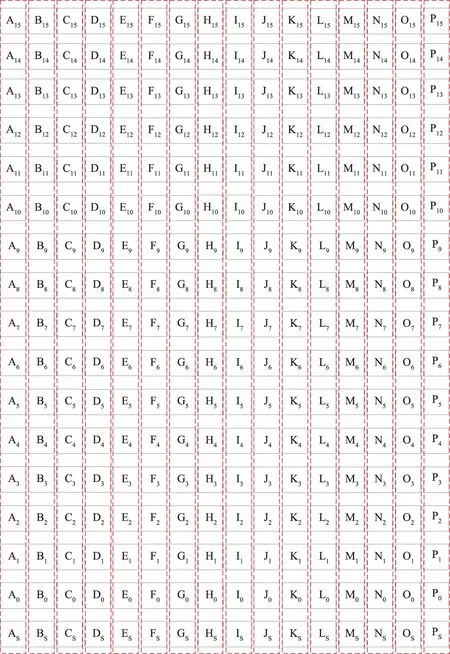
图4 重排序后的数据的二进制排列方式Fig.4 Binary arrangement of reordered data
回忆残差计算结果,取值较大的数据大幅减少,数据集中在0值附近,这一结果表明,残差数据的高位存在有大量的0,经过重排序操作,这些高位0被集合到一起,构成了大量新的值为0的数据,这些0值数据连续重复。当预测越精确时,0值数据越多;当预测的一致性越好时(即残差数据波动平缓),低位数据位的一致性越好(即相邻的残差数据的同一低位数据位倾向于同时为0或同时为1,最低位除外),由低位数据位重构成的数据的连续重复性越好。
残差数据单元输出重排序后的数据给改进的RLE单元,注意此时的数据的概率模型已经完全不同于原始智能配电网监测数据的概率模型。
2.4 改进的RLE单元
如前所述,残差计算并不会对数据起到压缩作用,采用位平面方法的重排序操作也不会压缩数据,真正对数据进行压缩的是改进的RLE和其后的霍夫曼编码。
RLE是微软公司为AVI格式设计的一种编码方法,其基本原理是使用“数据长度+数据”的组合替代连续重复的数据;当原始数据中存在大量连续重复的数据时,使用该方法能有效减少数据存储所需的空间。原始RLE的缺点十分明显,对于连续重复性较差的数据,使用该方法不仅不能压缩数据,反而会使数据的体积膨胀。另外,在原始的RLE中,数据长度所占用的位数固定,其所能编码的连续重复数据的长度存在最大值;当连续重复数据的长度超过该值时,就只能视为2段不同的连续重复数据,这显著降低了RLE的效率,尤其是在存在超长长度的连续重复数据时。因此,针对本文所述的场合,必须对RLE进行改进以提高性能。
本文对RLE的改进如下:
a)定义3个及以上连续且重复出现的字节为连续重复字节。
b)除连续重复字节的情况外,任意字节皆为连续非重复字节。
c)定义数据控制信息字节与数据值字节。数据控制信息字节的最高位表示数据为连续重复字节或连续非重复字节;次高位表示是否扩展数据控制信息字节,若不扩展,则数据控制信息字节为1个字节,若扩展,则数据控制信息字节的低6位表示扩展字节数。
d)定义RLE的格式为数据控制信息字节在前,数据值字节在后,即每组数据控制信息字节后必然跟随一组数据值字节。
e)当连续重复字节或连续非重复字节的连续长度小于或等于64时,数据控制信息字节不扩展,长度为1,且低6位表示连续重复字节或连续非重复字节的连续长度;当连续重复字节或连续非重复字节的连续长度大于64时,数据控制信息字节扩展,其后扩展的字节表示连续重复字节或连续非重复字节的连续长度。
f)当出现连续重复字节时,数据控制信息字节后只跟随1个数据值字节,数据值为连续重复字节的值;当出现连续非重复字节时,数据控制信息字节后跟随长度为数据控制信息字节所指示长度的数据值字节,即为对应的连续非重复字节。
经过上述改进,原始RLE的缺点得到有效改正。针对大量连续非重复数据,仅为这些连续非重复的数据附加一组控制数据,数据膨胀问题得到有效控制。即使对于改进的RLE而言最差的数据类型,这类数据的压缩比为68/69,远优于原始RLE的最差压缩比2。而对于其他情况,改进的RLE也具有更加优秀的性能。由于控制字节长度可以自由扩展,原始RLE的最大长度限制被解除。对于智能配电网的监测系统,由于其残差数据的取值范围要远小于原始监测数据的取值范围,经重排序后,出现大量连续重复的0值数据,采用改进的RLE,可以显著压缩数据容量。
经改进的RLE单元编码后的数据会被霍夫曼编码单元再次编码。两者结果取优,可实现数据进一步压缩。
3 仿真验证结果
本文分别对所提智能配电网监测数据的预测方法与基于预测的无损数据压缩方案进行仿真验证,以证明预测方法与压缩方案皆行之有效。
首先对本文所提智能配电网监测数据的预测方法进行仿真,测试信号由式(7)生成,类型为模拟智能配电网监测系统中的采样值数据。
sn=2cos(99πknTs)+
0.4cos(200.6πknTs+π/3)+
0.4cos(401.4πknTs+2π/3)+
0.2cos(807.4πknTs+π).
(7)
式中:kn为采样序列;sn为kn时的采样值数据;Ts为采样间隔(0.25 ms)。
仿真结果如图5所示,仿真中采用了2种方法对模拟的智能配电网采样值监测数据进行预测以作对比。第1种方法为前值预测法;第2种方法为本文所提基于2阶泰勒公式的预测方法,其中λ=0.5。由图5可知:从波形上看,2种方法预测的结果都十分接近原始信号;相对于原始信号数据的取值,2种方法的残差数据的取值都大幅减小。这一结果为本文所提的无损数据压缩方案奠定了压缩的基础。本文所提基于2阶泰勒公式的预测方法的预测效果要远好于前值预测法,基于2阶泰勒公式的预测方法不仅在预测精度上远超过前值预测法,在一致性上也表现良好,残差数据波动平缓,十分适合本文所提改进的RLE算法。
模拟的采样值数据在过0点时的取值可能会小于对应的残差数据的取值,定义预测数据的平均残差比
(8)
式中Ra为平均残差比。图5中,前值预测法的平均残差比为0.009 8,基于2阶泰勒公式的预测法的平均残差比为0.002 6,基于2阶泰勒公式的预测法的精度约是前值预测法的4倍。
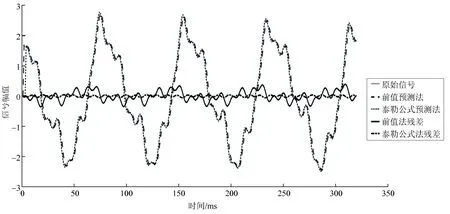
图5 智能配电网监测系统数据预测方法的仿真结果Fig.5 Simulation results of data prediction methods for monitoring system of smart grid
为了更加直观地论证本文所提基于预测的无损压缩方案的有效性,接下来,通过对一组仿真数据的实际压缩过程来验证。
表1是一组由仿真得到的智能配电网监测系统的采样值仿真数据,已经预先通过预测得到了其监测数据的预测值,这组数据一共包含16个监测点,采样精度为16位,采样值数据占用2个字节,用十六进制表示。表1第4列为计算得到的残差数据,用二进制表示。对残差数据进行重排序操作,得到重排序后的数据,见表2,同样采样二进制表示。表1残差值的行等于表2的列,这就是重排序操作的本质。
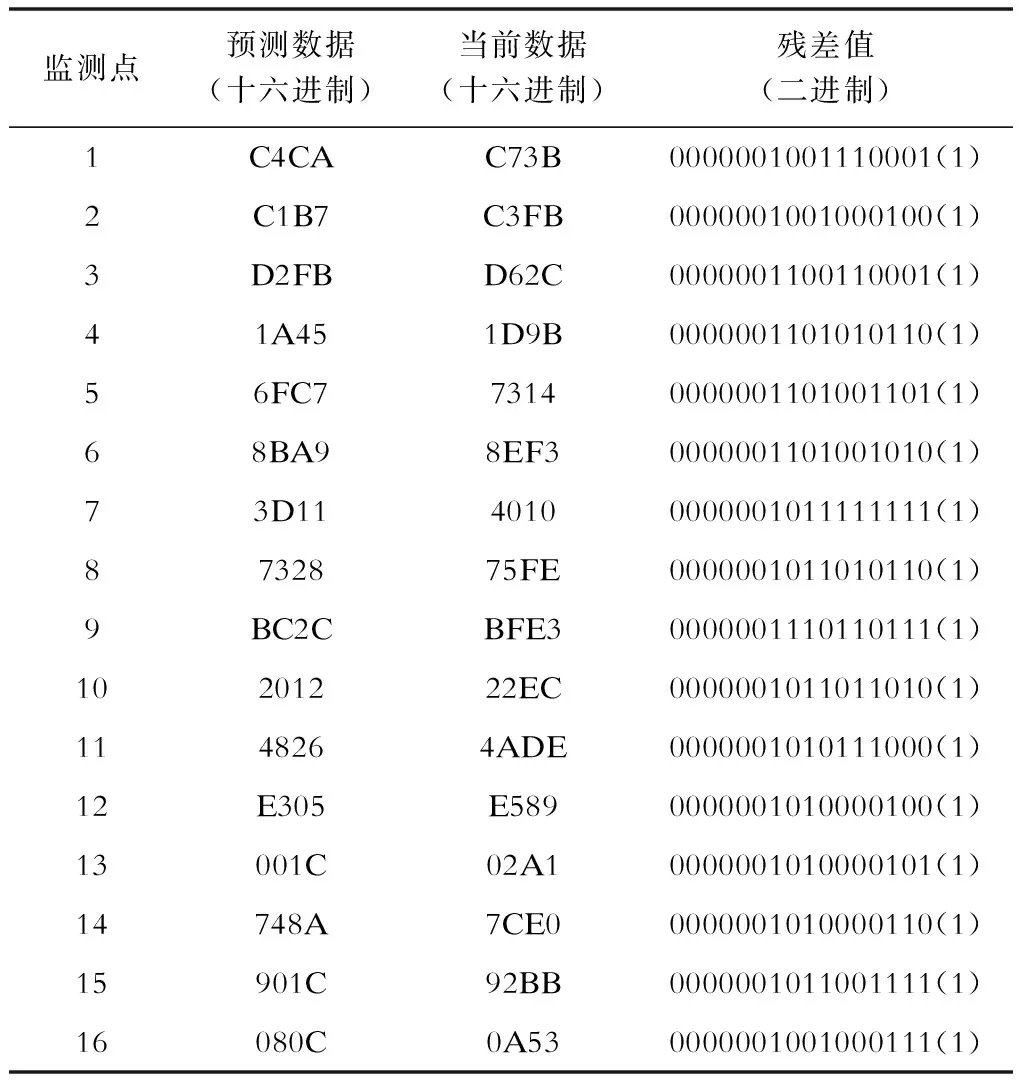
表1 智能配电网监测系统的采样值仿真数据Tab.1 Simulation data of sampling values for monitoring system of smart grid

表2 重排序后的表1数据Tab.2 Reordered data of Table 1
将重排序后的数据1个字节视为1个数据,共计34个数据,依次为00 00 00 00 00 00 00 00 00 00 00 00 FF FF 3C 80 03 FE DF 43 A2 A0 B3 E0 0E 62 5B 9F 17 C3 AA 8B FF FF。对其执行改进的RLE,得到最终输出的压缩数据8C 00 16 FF FF 3C 80 03 FE DF 43 A2 A0 B3 E0 0E 62 5B 9F 17 C3 AA 8B FF FF共计25个字节,较原数据32个字节减少了7个字节,实现了数据压缩,压缩比为32/25。
由于本仿真实验的数据量较小(仿真中仅含16个监测点),执行霍夫曼编码不能带来压缩比的提升,因此在本仿真中经改进的RLE输出的数据即为最终压缩数据。实际上,被压缩的智能配电网监测系统的数据量越大,压缩效果越好。即使是在较少的数据时,如本文中的仿真案例,数据也被压缩减少了近1/4,因此本文所提基于预测的无损数据压缩方案的有效性是毋庸置疑的。
另外,本仿真是对不同监测点同一时刻的数据进行压缩仿真,这意味着本文所提压缩方案在理论上的实时性可以达到每采样1次即压缩1次的速度,实时性远超必须添加时间窗的DFT/FFT与DWT、CS。这里,本文所提压缩方法用到了智能配电网监测系统中信号在时间上的连续性,其本质是要求各个监测点的信号具有相同的采样精度,而这一要求,在智能配电网的监测系统中十分容易达到。
4 结束语
针对智能配电网中的海量数据传输问题,本文提出对智能配电网的数据进行压缩再传输的解决方法。为实现这一方法,设计一种基于预测的无损数据压缩方案,该方案采用基于2阶泰勒公式的预测方法。通过与前值预测法的对比以及仿真实例,验证了所提无损数据压缩方案的有效性与优越性。所提方案具有传统的DFT/FFT和近几十年来发展起来的DWT与最新的CS所不具备的高实时性,十分适合于数据传输过程中的压缩再传输。另外,本文所提方案还具有较强的适应性,可以用于多种智能配电网监测数据的压缩传输,适用面广,压缩性能也十分优秀,具有极高的实用价值。
