服役预应力混凝土空心板梁抗剪承载性能

杜孟林 宗周红,2 廖聿宸 李明鸿

(1东南大学土木工程学院， 南京 211189)(2东南大学爆炸安全防护教育部工程研究中心， 南京 211189)

预应力混凝土空心板梁桥因构造简单、施工便捷，广泛应用于公路桥梁尤其是平原区高速公路中.然而，由于早期设计与施工工艺的不足，以及长期服役中受到车辆超载的影响，空心板梁桥易产生钢筋锈蚀、铰缝失效、梁体裂缝等病害[1-2].随着运营时间的增长，在日益增加的交通量影响下，病害进一步加剧，对空心板梁桥的安全性能造成了极大的隐患[3-5].因此，探究预应力混凝土空心板梁服役多年后的有效承载性能具有重要的意义.

为研究荷载作用下服役空心板梁的承载性能，国内外学者开展了一系列研究.Zhang等[6-7]通过对服役多年预应力混凝土空心板梁开展抗弯承载力试验，发现其抗裂性能显著下降，刚度及应力安全储备均较小.黄平明等[8]研究表明，空心板梁桥的抗剪承载力比抗弯承载力安全冗余度小.Di等[9]对12片服役空心板进行破坏性试验，发现10 m跨径的空心板梁抗剪承载力安全富余量仅为5.3%.石书卿[10]对服役多年的空心板梁进行了单边加载的破坏性试验，发现14 m跨径的试验梁在正常使用状态下裂缝宽度不满足《公路桥涵养护规范》中的限值要求.由此说明，预应力混凝土空心板梁桥在现行运营荷载下安全储备较低，抗剪承载力安全隐患问题较为突出.

针对服役多年的13 m跨径预应力混凝土空心板梁桥，本文选取其拆除的一片单梁进行抗剪承载力试验，并利用有限元分析软件ABAQUS进行非线性全过程分析，研究其在服役多年后的抗剪承载能力.研究结果可为同类型桥梁的安全评估和设计、检修、加固提供科学依据.

1 空心板梁抗剪试验

1.1 空心板梁试件

本文试验构件为某高速公路改扩建工程中拆除的13 m空心板梁，原桥自2002年建成通车，服役已近20 a.根据先期现场检查结果，该桥部分板梁在运营中曾遭受重物撞击，出现较为严重的损伤，为安全起见，拆除全部旧桥重建.桥梁拆除时，空心板梁沿企口缝切开，刨铣桥面沥青铺装层，保留后浇层混凝土及铰缝混凝土.选择一片未受撞击的中梁作为试验对象，进行剪切破坏试验.在其他空心板梁无明显损伤处进行取芯和破拆，得到混凝土芯样和钢筋样本，开展材性试验.

空心板预制梁、后浇层、铰缝的混凝土等级均为C40，预应力钢筋为φs12.7 mm低松弛预应力钢绞线，纵向普通钢筋为R335钢筋，腹筋、铺装层钢筋及构造筋均为R225钢筋.预应力筋及普通钢筋截面布置见图1.

图1 空心板梁横截面钢筋布置图(单位:cm)

1.2 试验方案

试验前，对试件进行外观检查，未见明显的混凝土裂缝和侵蚀等病害现象.记录试件实际尺寸后对表面进行打磨和粉刷处理，并绘制网格线，以便观察记录试验中梁体裂缝的开展情况.根据试验设计方案布设应变片、位移计等传感器，并调试数据采集设备.正式加载前，各加载点预加10 kN作用力，消除试件及加载系统的非弹性应变，核查传感器及数据采集设备正常工作无异常后，卸载预压荷载，对所有设备进行平衡清零处理.

试验加载方案如图2所示.利用2个MTS 1 000 kN电液伺服作动器进行两点同步加载.试验过程中，依据两加载点截面梁底竖向位移相同的原则进行加载控制.具体加载过程如下：位移加载的速率为2 mm/min，混凝土开裂前每级加载位移为2 mm，持荷时间为5 min；混凝土开裂后每级加载位移为4 mm，持荷时间为5 min；试件进入强非线性阶段后，因变形发展迅速，每级加载位移保持4 mm不变，持荷时间调整为2 min.荷载连续3级不再增长并呈现出下降趋势后，停止加载，保存试验数据并卸载.

图2 空心板梁试验加载方案及测点布置(单位：m)

1.3 试验结果

1.3.1 裂缝发展与破坏形态

加载终止时试验梁裂缝的分布情况见图3，加载过程中裂缝宽度和高度的发展过程见图4.图中，h为斜裂缝高度；H为梁高；Ws为腹板裂缝最大宽度；Wf为底板裂缝最大宽度.由图可知，加载至488.25 kN时，一侧加载点截面梁底出现横向裂缝(见图3(b)中曲线①)，该侧作动器出现明显卸载现象.继续加载，横向裂缝迅速发展贯穿梁底，加载点外侧出现腹板斜裂缝(见图3(a)中曲线②).加载至527.50 kN时，腹板斜裂缝开展高度超过梁高的65%，最大斜裂缝宽度达到1.3 mm，底板横向裂缝宽度达到1.7 mm.荷载增大至607.54 kN时，梁端腹板主斜裂缝侧出现新斜裂缝(见图3(a)中曲线③)，主斜裂缝高度超过梁高的90%，裂缝沿后浇层与铰缝接触面水平发展(见图3(a)中曲线④)，斜裂缝宽度达到3.5 mm；梁底沿预应力失效部位连线出现八字形裂缝(见图3(b)中曲线⑤)，底板裂缝宽度达到2.1 mm.继续加载，斜裂缝高度缓慢发展，裂缝宽度迅速增大，达到极限荷载733.42 kN时，腹板斜裂缝最大宽度为15.0 mm，底板裂缝宽度为10.0 mm.终止加载时，主斜裂缝高度达到梁高的95%，最大斜裂缝宽度为25.0 mm，底板裂缝最大宽度为12.0 mm，梁端后浇层、铰缝混凝土与预制梁明显脱空.

(a) 腹板裂缝(侧视图)

(b) 底板裂缝(俯视图)

图4 试验梁裂缝发展规律

试验梁的最终破坏形态为加载点截面纵筋、腹筋、预应力筋全部屈服，腹板斜裂缝基本贯穿至梁顶，加载点产生塑性铰.

1.3.2 荷载-位移曲线

图5给出了试验梁加载全过程的跨中截面荷载-位移曲线.由图可知，在加载初期，试验梁跨中挠度随荷载增加而线性增大，说明其处于弹性阶段.加载至488.25 kN时，荷载-位移曲线斜率明显减小，且不再呈线性变化，表明试验梁发生了塑性损伤，这与该荷载下试验梁出现第1条裂缝的试验现象相对应.试验梁开裂瞬间，观察到梁端预应力筋发生滑移，开裂侧作动器出现明显卸载现象，表现为荷载-位移曲线出现明显波动.加载至730.12 kN时，试验梁挠度迅速增大而荷载基本不变，荷载-位移曲线进入平直段，并达到极限荷载733.42 kN.随后，荷载-位移曲线进入下降段，位移急剧增大而荷载下降，试验梁丧失承载能力，加载随即终止.

图5 试验梁跨中荷载-位移曲线

1.3.3 抗剪承载性能分析

由试验结果可知，试验梁抗剪极限承载力为733.42 kN，加载点截面最大剪力值为369.25 kN；试验梁抗剪承载力设计值为324.04 kN，实测值与设计值之比为1.14；公路Ⅰ级(JTG D60—2015)[11]汽车荷载作用下，按实桥横向分布计算得到的中梁最大剪力效应值为347.39 kN，抗剪承载力实测值与最大剪力效应值之比为1.06.由此表明，本文试验的预应力混凝土空心板梁在服役近20 a后抗剪承载力仍满足要求，但相较于按规范[11]计算所得的剪力效应设计值，安全富余量仅为6%.

试验梁开裂时，实测跨中挠度为11.10 mm，不到跨径的1/1 150；达到极限荷载时，实测跨中挠度为62.13 mm，约为跨径的1/200；极限荷载与开裂荷载之比为1.5，对应跨中挠度之比为5.6.由此表明，该预应力混凝土空心板梁在服役近20 a后仍具有良好的刚度和延性.

2 空心板梁有限元模拟

2.1 有限元模型

根据试验梁原设计图纸和实测几何尺寸，利用有限元分析软件ABAQUS建立试验梁的三维精细有限元模型(见图6).由于实际斜交角较小，且试验时斜交角位置已超出支座，故建模时予以忽略.混凝土采用C3D8单元，预应力筋及普通钢筋均采用T3D2单元，共计66 005个单元.针对试验梁受剪为主的受力特点，网格划分时综合考虑计算精度及成本，梁端4 m范围内网格尺寸取为0.05 m，跨中非剪跨区网格尺寸取为0.10 m.

(a) 混凝土单元图

试验梁已服役多年，预应力损失难以确定.文献[5]指出，服役近20 a的既有预应力空心板梁剩余有效预应力值约为77%.通过降温法施加钢绞线预应力，钢绞线线膨胀系数为1.2×10-5，经试算降温值取485 ℃，加载点截面的有效预应力约为张拉控制应力的76%，与文献[5]的研究结论基本一致.后续数值模拟得到的荷载-位移曲线与试验结果吻合较好，进一步验证了有效预应力取值的合理性.

2.2 材料本构

2.2.1 混凝土材料本构

混凝土材料采用ABAQUS软件中的塑性损伤模型(CDP模型)模拟，单轴应力-应变关系依据《混凝土结构设计规范》[12]确定(见图7).依据材性试验结果，混凝土轴心抗压、抗拉强度和初始弹性模量分别取值为29.60、2.51和3.45×105MPa.

图7 混凝土应力-应变曲线

CDP模型需输入屈服准则、流动法则、滞回规则等对混凝土损伤进行定义.参考文献[13-15]，屈服面函数控制参数为0.667，膨胀角为30°，偏心距为0.1，双轴、单轴极限抗压强度之比为1.16，黏性系数为5×10-4.混凝土损伤因子取值见图8.

图8 混凝土损伤因子取值

2.2.2 钢筋材料本构

预应力钢绞线与普通钢筋材料均采用双折线弹塑性模型模拟.模型中考虑强化段，不考虑断裂失效，屈服应力、抗拉强度等材料参数依据《混凝土结构设计规范》[12]及材性试验取值.应力-应变关系和材料参数取值分别见图9和表1.其中，σs,y、σs,u分别为钢筋的屈服强度和极限强度；εs,y、εs,u分别为钢筋的屈服应变和峰值应变.

图9 普通钢筋及预应力钢绞线应力-应变曲线

表1 钢筋材料参数

2.3 边界条件

边界条件包括空心板梁的支承条件、钢筋与混凝土的连接、后浇层及铰缝混凝土与预制梁的连接以及施加的外荷载等.为减少支点及加载点应力集中的现象，建立刚性垫块模拟铰支座和加载梁，垫块可绕支点转动，垫块与空心板梁采用Tie约束，不考虑相对滑动.钢筋与混凝土之间采用Embedded约束，视为黏结良好，不考虑相对滑移.加载过程与试验情况一致，在Boundary Condition模块中对加载点垫块施加竖向强制位移，模拟位移控制加载.

后浇层、铰缝混凝土与预制梁接触面的黏结滑移和黏结失效行为通过Surface-based Cohesive Behavior模块进行模拟.参照文献[16]，滑移行为关键参数的取值如下：接触面法向、切向滑移刚度均为10 MPa/mm，总滑移值与塑性滑移值之比为2.参照文献[17-18]，接触面切向黏结强度fv=0.01fc，法向黏结强度fn=0.75ft，其中fc、ft分别为后浇层、铰缝和空心板混凝土轴心抗压强度和抗拉强度标准值中的较小值.损伤准则采用最大应力准则.黏结稳定性系数取为0.001.

2.4 有限元计算结果

2.4.1 裂缝发展

ABAQUS软件中CDP模型无法模拟裂缝的萌生和扩展过程，但可以通过塑性应变来识别裂缝位置及走向.图10给出了有限元模拟的试验梁混凝土塑性应变云图.比较图3和图10可见，建立的有限元模型可以较好地模拟剪跨区的斜向裂缝、非剪跨区的竖向裂缝、后浇层与铰缝交界处的裂缝、铰缝与预制梁之间的裂缝、梁底加载点横向裂缝和梁底剪跨区八字形裂缝等，且有限元计算的裂缝位置和开展情况与试验现象吻合良好.

图10 试验梁混凝土塑性应变云图

2.4.2 荷载-位移曲线

图11给出了试验梁跨中荷载-位移曲线的实测和数值模拟结果.可以看出，计算曲线与实测曲线在弹性阶段和非线性阶段均吻合良好，开裂荷载、极限荷载等特征荷载值及对应位移值的计算误差均在5%以内.在梁体开裂初期，观察到预应力筋发生了滑移，在有限元分析中未能考虑这一现象，导致该阶段挠度实测值略大于有限元计算值.总体而言，计算结果与实测结果吻合良好，说明建立的精细化有限元模型能较好地分析预应力混凝土空心板梁的非线性受力行为.

图11 试验梁跨中荷载-位移实测值和计算值对比

2.4.3 钢筋应力-荷载曲线

因试验梁为服役桥梁拆除所得，内部钢筋无法布置应变测点，试验中无法测量加载过程中钢筋的受力情况，故利用建立的有限元模型对内部钢筋应力进行分析.图12给出了加载点截面的腹筋、纵筋和预应力钢绞线应力与荷载的对应关系.由图可知，加载前，试验梁纵向钢筋和腹筋均无应力，预应力钢绞线最大应力约1 100 MPa.加载初期，腹筋应力基本无变化，纵向钢筋应力缓慢增长，荷载主要由混凝土和预应力钢绞线承担，表明腹筋对开裂荷载的控制作用很小.试验梁开裂时，预应力钢绞线最大应力约1 238 MPa，纵向钢筋最大应力约54 MPa.试验梁开裂后，钢筋应力迅速增长，总荷载达到611.36 kN时，加载点截面纵向纵筋受拉屈服；加载至622.36 kN时，加载点附近腹筋出现屈服；加载至691.35 kN时，加载点截面钢绞线屈服；达到极限荷载时，加载点截面附近的钢筋均已大面积屈服，表明试验梁为适筋梁，在剪切荷载下发生延性破坏，不会出现较危险的脆性破坏.

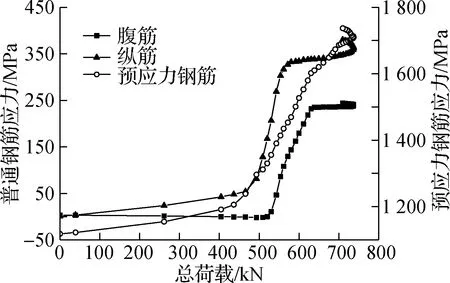
图12 钢筋应力-荷载关系

3 抗剪承载力影响因素分析

3.1 后浇层及铰缝

空心板试验梁在拆除时沿企口缝切开，刨铣桥面沥青铺装层，保留后浇层及铰缝混凝土，这部分与预制梁之间实际形成了新旧混凝土黏结面.荷载较大时，黏结面将发生失效破坏，新旧混凝土界面产生相对滑移.本文建立的有限元模型考虑了后浇层、铰缝与预制梁之间的黏结滑移行为.有限元计算结果表明：界面失效滑移主要集中在梁端剪跨区；加载至极限荷载时，最大相对滑移量达到2 mm；加载终止时，新旧混凝土界面的相对滑移情况见图13.图中变形比例因子为20倍，红色框内滑移现象明显.

本文通过ABAQUS软件中的Surface-based Cohesive Behavior模块模拟铰缝及后浇层与预制梁之间的黏结滑移行为，参数取值较为复杂，计算收敛存在难度.在实际工程中，为节省计算成本，往往对有限元模型进行简化处理.常用的简化建模方式有2种：①不考虑铰缝、后浇层与预制梁之间的滑移行为；②不考虑铰缝和后浇层对空心板梁承载力的贡献.采用简化建模方式1，将原模型(记为模型1)中黏结界面的Cohesive Behavior接触简化为Tie约束，得到模型2.采用简化建模方式2，在模型中删去铰缝、后浇层、后浇层钢筋网和多余约束，将加载点相应移至预制梁顶，得到模型3.

图13 梁端后浇层、铰缝与预制梁之间的相对滑移

采用3种有限元模型得到的抗剪极限承载力计算结果见表2.由表可知，后浇层及铰缝对空心板梁抗剪承载力贡献达15%以上，忽略该部分贡献使计算结果偏于保守.忽略后浇层及铰缝与预制梁黏结界面滑移的影响使抗剪承载力计算值偏高约5%，因此在简化计算时应对结果进行折减，折减幅度不小于5%.

表2 不同模型的抗剪极限承载力计算结果

3.2 预应力损失

预应力损失对空心板梁受力性能存在影响.可采用降温法模拟不同的有效预应力值，比较空心板梁在不同预应力损失下的抗剪承载力.2.1节中试验梁的钢绞线降温幅值为485 ℃，加载点截面预应力损失约为24%，计算结果与试验梁实际状态吻合.降温幅值为450 ℃时，预应力损失值L=30%；降温幅值为550 ℃，L=14%；降温幅值为611.84 ℃，L=4%.

图14给出了不同预应力损失情况下空心板梁的跨中荷载-位移曲线.由图可知，不同预应力损失工况下空心板梁开裂前刚度基本一致，开裂后刚度随预应力损失的增大而减小.表3列出了不同预应力损失情况下空心板梁的开裂荷载、极限荷载及达到极限荷载时跨中挠度计算值相较于L=24%工况时的变化幅值.由表可知，各工况下极限荷载变化幅值小于2%，表明预应力损失对空心板梁抗剪极限承载力影响较小.与L=4%的空心板梁相比，L=30%的空心板梁在极限荷载作用下跨中挠度增大60%以上，表明预应力损失对空心板梁在极限荷载下的挠度影响较大.此外，空心板梁开裂荷载受预应力损失影响较大，与L=4%的空心板梁相比，L=30%的空心板梁的开裂荷载减小约25%，开裂荷载值随预应力损失的增大而显著减小.

图14 不同预应力损失下跨中荷载-位移曲线

表3 不同预应力损失下梁关键响应参数变化幅值

4 结论

1) 本文采用的预应力混凝土空心板梁在服役近20 a后抗剪承载力仍满足公路Ⅰ级汽车荷载作用下的剪力效应设计值要求，但安全富余量仅为6%.

2) 试验梁开裂时，实测跨中挠度为11.10 mm，小于跨径的1/1 150.试验梁极限荷载与开裂荷载之比为1.5，对应跨中挠度之比为5.6.由此表明，该预应力混凝土空心板梁在服役多年后仍具有良好的刚度和延性.

3) 利用ABAQUS软件建立的精细化有限元模型能够较好地模拟预应力混凝土空心板梁剪切破坏全过程非线性行为，可为同类空心板梁抗剪承载能力分析提供参考.

4) 后浇层及铰缝对空心板梁抗剪承载力贡献达15%以上，但其与预制梁间的黏结滑移行为对抗剪承载力影响较小.在空心板梁抗剪极限承载力计算中，可将后浇层、铰缝与预制梁作为整体建模以简化计算，但需要对抗剪承载力计算结果考虑不小于5%的折减.

5) 预应力损失对空心板梁的抗剪极限承载力影响较小，但对开裂荷载和极限承载力对应挠度的影响显著.预应力损失越大，空心板梁裂缝出现越早，开裂后刚度损失越迅速.