考虑震损的混凝土框架结构改进建模方法

杨 昀 徐赵东 Abid Ali Shah 董尧荣 胡钟玮 黄 娥

(1东南大学土木工程学院， 南京 210096)(2Department of Civil Engineering, International Islamic University, Islamabad 30001, Pakistan)

我国结构抗震设计一般遵循“三水准”的设防目标，即允许结构在中强震作用下出现一定程度的损伤.结构出现损伤后，如果不能及时对其进行评估修复，后续余震可能导致结构损伤加重甚至倒塌.在早期对震后结构加固修复的研究中，结构震损经常被忽略，等效于对完好结构的加固修复进行研究，这与灾区重建面临的工程实际不甚相符[1].

5·12汶川地震后，国内学者对震损结构的加固修复开展了较多的试验研究，如周云等[2]采用拟静力加载使足尺框架试件产生损伤，再加入减震墙板研究加固结构的抗震性能.相较于试验研究，相关的数值模拟研究则较少，其核心问题在于结构的震损难以在结构数值模型中加以合理考虑.鉴于此，尹帅锋等[3]依据构件损伤指数，对混凝土的强度及初始弹性模量进行折减，以模拟损伤构件，但没有考虑强度、刚度的退化规律区别.韩建平等[4]对混凝土抗压强度及钢筋弹性模量进行折减，再采用纤维模型对震损框架结构进行建模.周小龙等[5]基于改进IMK模型，研究了损伤构件的骨架曲线退化规律，并将其应用于震损结构建模中；孙艳等[6]将文献[5]的结论应用到碳纤维布加固震损型钢筋混凝土柱的有限元建模中，模拟结果与试验吻合良好；李英明等[7]则在文献[5]的基础上增加了一个描述构件耗能性能退化的参数，但参数定义存在一定缺陷.

本文在文献[5]的基础上增加考虑了损伤构件的滞回规则退化，即除强度退化指数αM、刚度退化指数αK外，补充定义了滞回耗能退化指数αγ，对结构性能数据库(SPD)中获取的试验数据进行回归分析，建立并验证了基于统计学综合性能退化的损伤构件恢复力模型.对完好结构输入2种地震的组合地震波，对震损结构输入单一的地震波，对比这2类结构的弹塑性时程分析结果，以证明该震损结构建模方法的准确性.

1 损伤构件恢复力模型

1.1 性能退化指数

钢筋混凝土构件的恢复力特性可由改进IMK模型进行描述[8-10].基于该模型，将损伤构件的力学性能退化视为由骨架曲线退化和滞回规则退化两部分构成.针对骨架曲线退化部分，根据改进IMK模型的第1种退化模式的定义[8]，经历i次循环的损伤构件的屈服强度Myd可表示为

(1)

式中，My为完好构件的屈服强度；βj为第j次循环退化指数.

损伤构件的弹性刚度Ked可表示为

(2)

式中，θyd为损伤构件的屈服位移；θbi为前i次循环过程中构件最大位移.

针对滞回规则退化部分，出于简化考虑，可将改进IMK模型对应4种退化模式下的退化速率指数假定为1，将滞回耗能参数统一定义为γ.若将经历i次循环后的损伤构件视为一新构件，则该构件第1次循环结束点的循环退化指数βd,1应等于完好构件第i+1次循环结束点的循环退化指数βi+1，即βd,1=βi+1，由此可求得损伤构件的滞回耗能参数γd为

(3)

式中，Ei+1为构件在第i+1次循环中耗散的能量.

根据式(1)～(3)，损伤构件的3项性能退化指数(强度退化指数αM、刚度退化指数αK及滞回耗能退化指数αγ)可定义如下：

(4)

1.2 恢复力模型的建立

分别根据Park-Ang模型[11]和Kunnath模型[12]，采用统计学回归分析方法，提出基于统计学综合性能退化的损伤构件恢复力模型，以定量描述构件3项性能退化指数αM、αK、αγ与损伤指数间的关系.

回归分析所用的数据从美国太平洋地震工程研究中心建立的SPD数据库中获得[13].回归分析时选用的钢筋混凝土构件需满足以下4点要求：① 轴向压力为定值；② 抗震构造良好；③ 截面为矩形；④ 最终破坏形式为受弯破坏.

基于上述要求，共筛选出61组构件的循环往复加载试验数据进行计算，最终可得3项性能退化指数与Park-Ang模型损伤指数D的定量关系式为

(5)

αM、αK、αγ与Kunnath模型损伤指数D′的定量关系式为

(6)

基于Park-Ang模型和Kunnath模型的拟合曲线见图1.

(a) αK-D曲线

(d) αK-D′曲线

2 损伤构件恢复力模型验证

2.1 基于Park-Ang模型的恢复力模型验证

采用OpenSees软件模拟钢筋混凝土构件在损伤状态下的往复加载过程，对基于Park-Ang模型的损伤构件恢复力模型进行验证.在SPD数据库中选取2个未参与回归分析的构件作为研究对象，并采用“零长度单元+弹性梁柱单元” 的组合形式对构件进行建模，其中，零长度单元使用峰值指向型的改进IMK模型材料定义，相应的材料参数见表1.表中，Ke、Ks、Mc分别为完好构件的弹性刚度、屈服后刚度和极限强度.对完好构件进行循环往复加载模拟，结果见图2.由图可知，模拟结果与试验结果吻合良好，说明该建模方式可有效模拟RC构件循环往复加载过程，且材料参数定义准确.

表1 完好构件中改进IMK模型材料参数

(a) 1#构件

(b) 2#构件

钢筋混凝土损伤构件的损伤程度随循环圈数的增加而逐渐增大.为评估基于Park-Ang模型的恢复力模型对构件不同损伤状态的描述能力，分别在2个构件的卸载曲线上各选取2个验算点，分别对应不同的循环圈数，计算构件对应的Park-Ang模型损伤指数D，并通过式(5)计算得到3项性能退化指数.基于各性能退化指数，可对表1中的材料参数进行折减，得到损伤构件的材料参数(见表2).对不同损伤状态下损伤构件的加载过程进行模拟，结果见图3.由图可知，2种构件的滞回曲线峰值模拟结果和试验结果的误差均小于10%，即模拟结果和试验结果吻合良好，由此证明了基于Park-Ang模型的损伤构件恢复力模型的准确性.

表2 损伤构件模型中改进IMK材料参数

(a) 1#构件, D=0.172

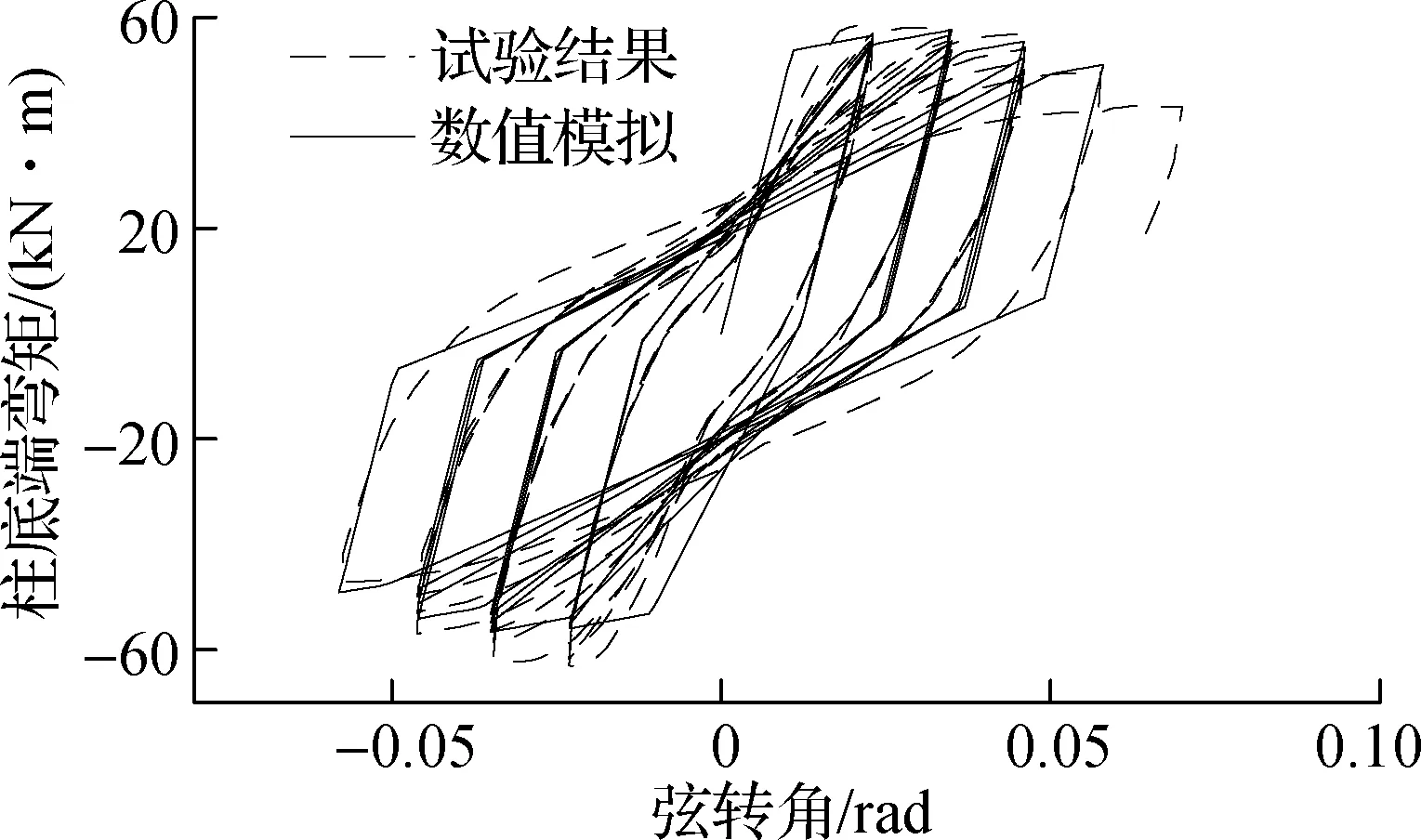
(c) 2#构件, D=0.150

2.2 基于Kunnath模型的恢复力模型验证

根据式(5)和(6)，计算1#构件和2#构件在各验算点处的各性能退化指数，以验证基于Kunnath模型的恢复力模型的准确性.2个构件的性能退化指数对比结果见图4，为便于比较，将横坐标统一取为Park-Ang模型损伤指数D.进一步计算可知，Park-Ang模型拟合所得的αM、αK、αγ标准差分别为0.085、0.111、0.107，Kunnath模型拟合所得的标准差分别为0.085、0.097、0.098.由此可知，Kunnath模型在精确性上略优于Park-Ang模型.当D<0.3时，基于Park-Ang模型的损伤构件恢复力模型更为保守；当D>0.3时，基于Kunnath模型的损伤构件恢复力模型更为保守.

就适用范围而言，由于Park等[11]曾对构件损伤等级进行划分，并给出了各等级对应的损伤指数范围与表观损伤，因此基于Park-Ang模型的损伤构件恢复力模型更适用于基于表观损伤的震损结构建模；而对于数值模拟时由输入地震波产生损伤的结构模型，为得到更加精准的结果且避免对仍处于弹性阶段的构件进行多余计算，可优先考虑基于Kunnath模型的损伤构件恢复力模型.

3 震损结构的建模方法

某5层钢筋混凝土平面框架结构立面见图5.

(a) 1#构件

(b) 2#构件

图5 框架立面构造及塑性铰分布图(单位：mm)

各楼层梁柱尺寸一致，所用混凝土强度等级均为C35，纵筋强度等级为HRB400，箍筋强度等级为HPB300.平面框架荷载见表3.建模时，构件采用“零长度单元+弹性梁柱单元+零长度单元”组合的方式建立，即在各梁柱节点周边定义零长度单元，零长度单元之间由弹性梁柱单元连接.其中，零长度单元使用峰值指向型的改进IMK模型材料定义，材料参数可根据文献[14]中的经验公式计算.

表3 平面框架荷载

震损结构可通过向完好结构中输入一段地震波得到.记录地震波作用下各零长单元力-位移的时程曲线，可得到基于Kunnath模型的损伤指数D′，并按式(6)计算得到损伤构件对应的性能退化指数αM、αK、αγ.采用2.1节中方法，对完好模型中的峰值指向型材料参数进行折减，即可得到所需的震损结构模型.其中，地震波选用峰值加速度为4 m/s2的Hollister波，持续时间为40 s(见图6).在该地震波作用下结构会产生一定的损伤，通过记录各零长单元力-位移的时程变化可知，70个零长单元中共22个单元进入塑性阶段(见图5)，分布于首层柱底端和1～3层梁端.

(a) 组合波

(b) 单一波

利用OpenSees软件进行弹塑性时程分析时，可通过对完好结构模型输入Hollister波(持时40 s、峰值加速度0.4g)与Taft波(持时30 s、峰值加速度0.2g)的组合波(中间加入10 s的空白段，见图6(a))，同时向震损结构模型中输入同样的单一Taft波(见图6(b))，对比完好结构模型及震损结构模型在Taft波作用阶段主要楼层的位移时程曲线，验证所提震损结构建模方法的准确性.为扣除残余变形的影响，进行更为直观的比较，将震损结构模型输入单一地震波后的位移时程曲线上下平移(见图7).由图可知，向震损结构模型输入单一地震波与向完好结构模型输入组合地震波时，各楼层位移时程曲线50 s后的部分基本吻合，说明基于统计学综合性能退化的损伤构件恢复力模型进行震损结构建模是可靠的.

(a) 底层位移

(b) 第3层位移

(c) 顶层位移

4 结论

1) 本文从损伤构件的骨架曲线退化和滞回规则退化两方面定义了强度退化指数αM、刚度退化指数αK及滞回耗能退化指数αγ.通过对SPD数据库中61组构件试验数据进行回归分析，得到了基于统计学综合性能退化的损伤构件恢复力模型.

2) 采用OpenSees软件对2组构件在损伤状态下的往复加载过程进行模拟，模拟结果与试验结果吻合良好，各组构件滞回曲线力峰值的理论值和试验值误差均小于10%，从而验证了基于Park-Ang模型的损伤构件恢复力模型的准确性.进一步对比了基于Park-Ang模型与Kunnath模型的损伤构件恢复力模型，发现两者的准确性相似，但在适用范围上存在差异.

3) 采用所提出的损伤构件恢复力模型进行震损结构建模.向完好结构模型输入Hollister波与Taft波的组合地震波，向震损结构模型输入单一Taft地震波，进行弹塑性时程分析，对比2种模型的位移时程曲线.结果表明，二者吻合良好，从而验证了该震损结构建模方法的可行性.