基于自组织映射(SOM)算法的地下水污染源反演

郑 哪,江思珉,*,刘金炳,程 璐,王智源,栗现文

(1.同济大学土木工程学院水利工程系,上海 200092;2.南京水利科学研究院水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;3.西北农林科技大学水利与建筑工程学院,陕西 咸阳 712100)

与地表水相比,地下水一旦遭受污染，其治理与修复往往需要更长的时间(常常持续30年以上),且治理与修复费用往往极为昂贵。对于地下水污染治理，首要任务是要弄清地下水污染源信息(包括地下水污染源分布以及污染物排放信息等)。但由于地下水污染发生的隐蔽性和发现的滞后性，加之地下水监测井数量较少，往往很难直接获得地下水污染源信息以及场地水文地质参数。针对这种情况，需要采用地下水逆问题的求解方法(反演法)，即通过较少的观测信息反推地下水污染源信息。

目前对于反演问题的求解方法主要有3种：直接方法、优化方法和随机方法。反向追踪方法作为一种常用的直接方法，可以通过当前地下水中污染物分布条件，估计之前某一时刻地下水中污染物的分布，最终实现对地下水污染源位置和污染物释放历史的确定。如曹彤彤等将伴随状态方法分别应用于均质与非均质含水层的单点和多点地下水污染源特征识别，以达到对地下水污染源位置进行有效识别的目的，但随着地下水污染源数量的增加，该方法的计算精度显著降低，其稳定性较差。优化方法是通过寻找使目标函数最小的参数组合来确定地下水系统模型参数的一种方法，但该方法仅能得到一组最优参数组合，无法解决地下水系统模型参数的不确定性问题。随机算法因具有同时更新地下水模型参数值和模型参数分布的优势而被广泛应用。如江思珉等利用卡尔曼滤波方法更新地下水采样点，实现了以较少的采样点来识别地下水污染源的位置；崔尚进等将U-D分解引入常规卡尔曼滤波，在假想算例下对多个潜在污染源的综合污染羽进行更新，最终实现了对真实地下水污染源的识别，但该方法对地下水采样点信息的要求较高，有时不能达到收敛要求。利用优化方法和随机算法对地下水污染源进行反演时都需要反复调用地下水系统模型，导致计算代价较高、计算时间较长。因此，为了提高计算效率，通常会构造替代模型来替代地下水系统原始模型，以较低的计算代价对原始模型的主要特征进行提取和近似，从而得到原始模型输入与输出之间的关系。目前，数据驱动(Data-driven)类的替代模型较为流行，主要是通过研究原始模型输入与输出数据之间的内在联系构造替代模型，其中常见的构造方法包括径向基函数(RBF)、支持向量机(SVM)、混沌多项式展开(PCE)、高斯过程(GP)和人工神经网络(ANN)等。如王宇等基于小波变换理论与人工神经网络建立替代模型，该模型在功能上逼近地下水流数值模拟原始模型，说明小波神经网络模型能够降低计算效率，有效替代原始模型；Hazrari-Yadkoori等采用自组织映射(SOM)算法来表征地下水系统模型的输入与输出的响应关系，提高了替代模型的性能。

作为一种数据挖掘技术，SOM算法通过对原始数据的变换突出其非线性关系，适合作为处理非高斯问题的解决方法，该算法主要通过计算输入数据间的主要特征和相关关系，将高维数据转换为低维数据，有效提升了数据处理能力，进而提高了计算效率。在地下水污染溯源问题中利用SOM算法构建的地下水流数值模拟替代模型兼具模拟模型与优化方法的功能，其不仅能够近似预测估计地下水水流及溶质运移模拟模型的输出结果(即正演计算)，而且无需联合其他优化方法，直接利用训练好的替代模型即可直接进行地下水污染源信息识别(即反演过程)，这将进一步提高地下水污染溯源过程的求解效率。

本文提出一种基于SOM算法的地下水污染溯源模型替代模型的构建方法，并通过数值算例研究了SOM替代模型中训练数据样本数目和神经元数目的最优组合，以得到能够准确地表征地下水污染源强信息与观测数据之间联系的最优替代模型，该替代模型可以看作是一种快速反演算法(一旦SOM替代模型构建完成，则可以根据观测信息快速推估地下水污染源信息)，最终实现对地下水污染源快速辨识的目的。

1 基于SOM算法的地下水污染溯源模型的替代模型构建方法

地下水污染溯源问题是通过使地下水观测点的实测值与模拟值的偏差达到最小，从而获取地下水污染源信息(包括污染源位置、污染物排放浓度和排放时间等)以及未知含水层参数(主要包括含水层渗透系数场、贮水系数、弥散度、有效孔隙度等)。

1.1 地下水污染迁移模型

目前常用的地下水中污染物迁移模拟程序有MOC3D、MT3DMS、RT3D、FEMWATER、FEFLOW等。其中，MT3DMS是应用最为广泛的地下水中污染物迁移模拟程序。本文利用MODFLOW和MT3DMS程序构建地下水中污染物运移的数值模拟模型。MT3DMS程序本身不包括地下水水流模拟程序，模拟计算时，MT3DMS程序需和MODFLOW程序一起使用。

MODFLOW程序的地下水水流方程如下：

(1)

式中：假定含水层的渗透系数在主轴方向与坐标轴方向一致，

K

、

K

、

K

分别为含水层渗透系数在

x

、

y

、

z

方向上的分量[LT];

h

为水头[L]；

W

为单位时间从单位体积含水层流入或流出的水量[T]；

S

为孔隙介质的贮水率[L]；

t

为时间[T]。

MT3DMS程序的地下水溶质运移方程如下：

(

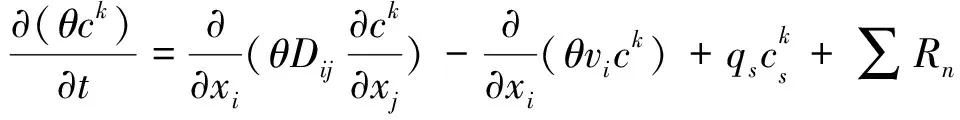
2)

1.2 自组织映射(SOM)神经网络学习算法

自组织映射(Self-Organizing Map,SOM)神经网络含有一个输入层和一个映射层，神经网络的输出体现在映射层。对于输入数据，初始化网络通过比较各神经元与输入之间的距离来计算判别函数值，其中具有最小判别函数值的特定神经元为获胜神经元；获胜神经元被激活后，其权值得到增强，随之根据输入数据的分布进行移动；获胜神经元拓扑邻域的神经元也会被不同程度激活，权值进行更新，随之移动。通过上述过程的不断进行，最终SOM神经网络会很好地体现所有输入数据的分布。

对于训练好的替代模型，SOM神经网络中神经元包含的信息被称为Map Codebook；当使用其进行正向预测或逆向源识别时，SOM替代模型通过计算神经元与输入向量之间的距离来确定获胜神经元，获胜神经元对应的Map Codebook中的数据向量被输出。使用SOM替代模型进行正向预测的流程，见图1。

图1 SOM替代模型正向预测的流程图Fig.1 Flow chart of forward prediction of SOM surrogate model注：SPn表示n个地下水污染源强度；Cm表示m个污染物 浓度观测值;h表示训练数据数量。

SOM神经网络的训练过程主要包括以下步骤：

第一步：SOM神经网络初始化。选择适当的学习率和网络节点数量对SOM神经网络进行初始化，其中学习率决定着收敛速率，网络节点影响着训练好的网络分布与训练数据分布的拟合程度。

第二步：竞争得到获胜神经元。对于不同的输入模式，网络中每个神经元通过下式计算自身的判别函数值，其中具有最小判别函数值的特定神经元为获胜神经元(BMU)。判别函数(平方欧式距离)的计算公式如下：

(3)

式中：

D

为输入维度；

x

为输入数据；为神经元

j

与输入数据

i

之间的权重向量。

第三步：定义拓扑邻域。在上一步得到获胜神经元(BMU)后，以该神经元为中心定义一个拓扑邻域：

(4)

式中：

I

(

x

)为BMU的索引；

S

为神经元

j

与获胜神经元之间的距离；

σ(t)

随时间线性递减。

第四步：调整。定义拓扑邻域后，邻域中的所有神经元会根据自身权重进行不同程度的更新，以适应不同的输入向量，其中获胜神经元权重更新幅度最大，其权重更新可表示如下：

Δ

=η(t)

·

T

(t)

·(

x

-

)

(5)

式中：

η

(

t

)为学习速率；

x

为输入数据。权重更新过程中，不断向对应的

x

移动，目的是得到与输入的训练样本相似的分布。

第五步：循环以上步骤，直至神经网络收敛。

2 数值算例研究

2.1 问题概述

如图2所示，某含水层为二维非均质各向异性的承压含水层(2 000 m×1 000 m)，用边长为100×100 m的网格将区域剖分为10行20列的有限差分网格。假设含水层水流运动为稳定流，含水层厚度为1 m。上、下边界为二类隔水边界，左边界为定水头边界(水头为15 m)，右边界为定水头边界(水头为10 m)，无其他源汇项。初始时刻，含水层中无污染物。含水介质的孔隙度为0.3，纵向弥散度为30 m，水平横向弥散度为3 m。

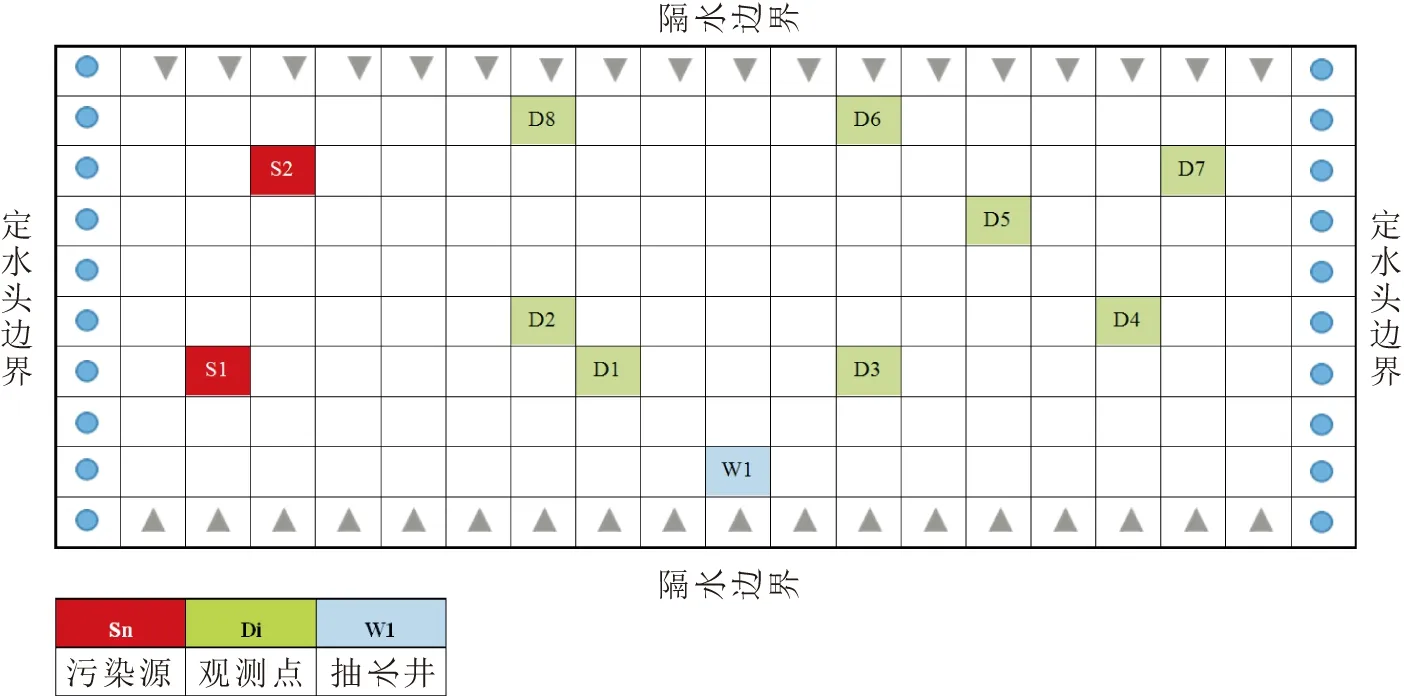
图2 地下水污染源、观测点和抽水井位置图Fig.2 Location of groundwater pollution source,observation point and pumping well

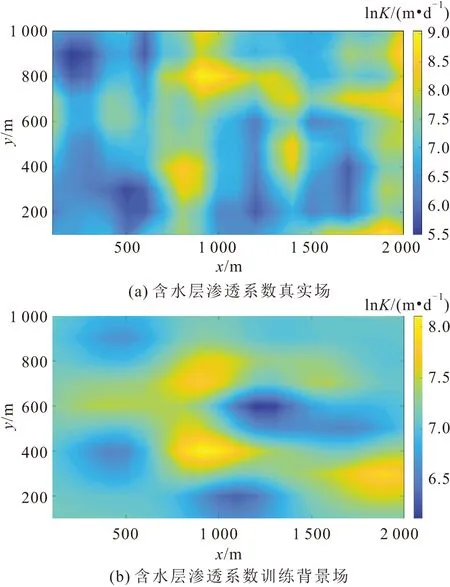
图3 某非均质含水层模型Fig.3 Heterogeneous aquifer model for the case study

该含水层存在点源污染，根据场地污染调查确定地下水污染源的位置为S1和S2(见图2)。本数值算例中，地下水观测点处污染物浓度值利用MODFLOW和MT3DMS程序正演计算得到，模拟时间为800 d，分为8个应力期(每个应力期100 d)，地下水污染源仅在前7个应力期释放污染物(见表1)，考虑两处地下水污染源和一种保守污染物。场地内共布置8个观测点(见图2)，取每个应力期结束时各观测点处污染物浓度值作为观测值。

表1 不同应力期地下水污染源强真值 Table 1 Reference values of groundwater contaminantsource parameters for the case study

2.2 结果与讨论

2.2.1 训练替代模型

由第1.2节可知，SOM训练样本和unit数量影响着Map Codebook的规模，因此构建SOM替代模型的过程中，重点讨论这两个重要参数。

构建SOM替代模型时采用的数据样本，见表2。该数据样本是利用拉丁超立方采样方法生成地下水污染源强(地下水污染源强估计区间为30～40 g/s)，通过在MATLAB环境下调用MODFLOW/MT3DMS实现地下水中污染物运移的模拟，从而得到观测点处污染物浓度值。上述地下水污染源强与其对应的观测点处污染物浓度值组成一个数据样本，该数据样本包括训练样本和测试样本(10折交叉验证法)，其中训练样本用来构建SOM替代模型，并根据不同训练样本得到的SOM替代模型对测试样本进行正向预测和地下水污染源识别计算，再将计算结果进行比较，以选出最佳SOM替代模型。

表2 SOM替代模型的样本规模Table 2 Sample sizes of SOM-based surrogate models

unit作为网络神经元的个数，决定着训练样本被划分的类别数。当神经元数量过少时，存在多组样本被划分到同一类别的现象，不能很好地体现出样本数据间不同的特征，导致SOM替代模型的预测精度较低。由于所有神经元都要计算自身与输入样本的欧氏距离，以判断获胜神经元，因而神经元数量过多时，其计算量将显著增大，导致训练模型所需的时间急剧增加。

2.2.2 最佳SOM替代模型

本次研究采用归一化估计绝对误差(NAEE)来评估基于SOM的替代模型的准确性。NAEE可以定量地对比SOM替代模型输出值与真实值之间的差距，通过归一化后可以表征SOM替代模型输出值相对真实值的偏离程度。作为一种评估SOM替代模型预测精度的指标，NAEE值越小，说明SOM替代模型的预测精度越高。

正向模拟时NAEE的计算公式为

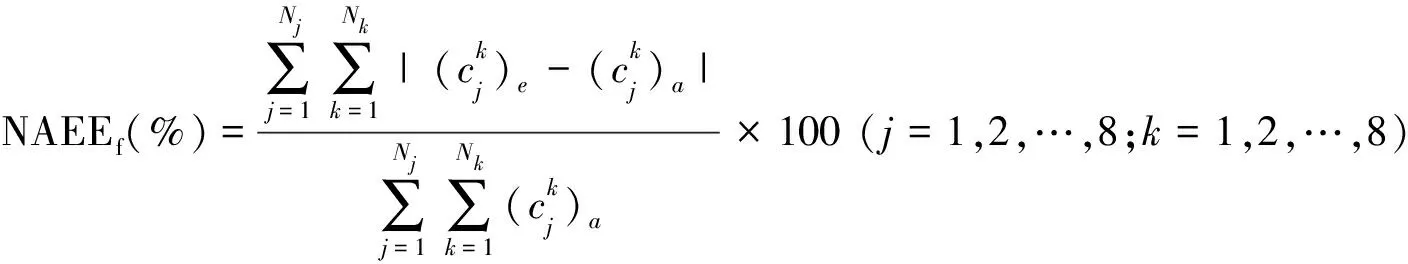
(6)

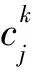
反演计算时NAEE的计算公式为

(7)

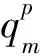
使用不同数量的训练样本和unit的组合得到多个SOM替代模型，利用测试数据分别进行：①地下水污染源强数据作为输入，预测污染物浓度观测值；②污染物浓度观测值作为输入，得到地下水污染源强信息。

利用所有训练好的SOM替代模型进行正向预测时，预测结果的NAEE平均值均小于6.4%，不同数量的训练数据得到的SOM替代模型的预测精度略有波动，但总体相差不大[见图4(a)]。利用所有训练好的SOM替代模型进行反演计算时，计算结果的NAEE平均值均小于8.6%，当unit从50增加到200时，所有SOM替代模型的计算精度呈显著提高趋势[见图4(b)]。根据对不同SOM替代模型的性能、不同数量训练样本生成所需CPU运行时间和unit对建立SOM替代模型时运行时间的影响三个方面的平衡分析，最终确定基于SOM的最佳SOM替代模型的unit为600、训练样本数量为1 800组。

图4 不同SOM替代模型预测和反演计算的NAEE值Fig.4 Predicted and inversed NAEE values of different SOM surrogate models

因此，基于SOM的替代模型用于正向预测和反演计算均能取得较好的效果，能够准确地表征地下水污染源强信息与观测数据之间的联系，对于输入数据中的缺失信息(地下水污染源强信息或观测值)，利用SOM替代模型能够实现预测模拟或进行地下水污染溯源计算。

2.2.3 地下水污染溯源分析

得到最佳SOM替代模型后，重点需要对地下水污染溯源识别结果的鲁棒性进行分析与讨论，即对考虑观测误差和未知抽水井影响下的基于SOM替代模型的地下水污染溯源识别结果的鲁棒性进行分析。

(1) 观测误差的影响。上述SOM替代模型的训练样本和测试样本均为无误差的情况，下面考虑污染物浓度观测值有不同程度误差时对地下水污染溯源结果的影响。如下式所示，污染物浓度观测值存在满足正态分布的测量白噪声，则有：

C

′

=C

+

ε

×

a

×

C

(8)

式中：

C

′表示引入误差后的污染物浓度观测值

;C

表示污染物浓度模拟值(无误差)；

ε

表示满足标准正态分布的随机偏差；

a

为噪声水平(5%、10%、15%、20%)。

20%观测误差与无误差情况下地下水污染源强度的反演结果对比，见图5。

图5 20%观测误差与无误差情况下地下水污染源强度的 反演结果对比Fig.5 Comparison of identification results of groundwater contaminant source fluxes at S1 and S2 at observa- tion error levels of 20% and zero

由图5可见，观测误差水平达到20%时,SOM替代模型对地下水污染源强度的识别精度虽较无误差情况略有下降，但总体趋势和数值仍能较好地贴近真值。

不同观测误差水平下的NAEE值，见图6。

图6 不同观测误差水平下的NAEEs值Fig.6 NAEEs values at different observation error levels

由图6可见，引入观测误差后，NAEE值由4.22%增至6.46%，远低于20%的误差水平,说明观测误差的引入对识别结果的影响不大，表明上述得到的最优SOM替代模型的鲁棒性较强。

(2) 未知抽水井的影响。地下水系统是一个受多种因素影响的复杂系统,存在着各种不确定性。在实际问题中,场地信息的不确定性还包括由于抽(注)水井、排水沟渠等调查数据的不完备所引起的不确定性。在该含水层南侧W1处(见图2)布置了一口流量为2 000 m/d的抽水井，考虑在抽水井信息未知条件下得到的最优SOM替代模型对地下水污染源强度进行反演，其反演结果见图7。

图7 未知抽水井影响下地下水污染源强度的反演结果Fig.7 Identification results of groundwater contaminant source fluxes at S1 and S2 with and without unknown pumping wells

由图7可见，当存在未知抽水井这一干扰因素时，SOM替代模型对地下水污染源强度的识别精度有所降低。引入观测误差后，NAEE值由4.22%增至8.31%，表明生成SOM样本的概念模型决定着SOM替代模型的正确性和识别精度的高低。

第400 d污染物扩散的真实情况和SOM替代模型的预测结果，见图8。

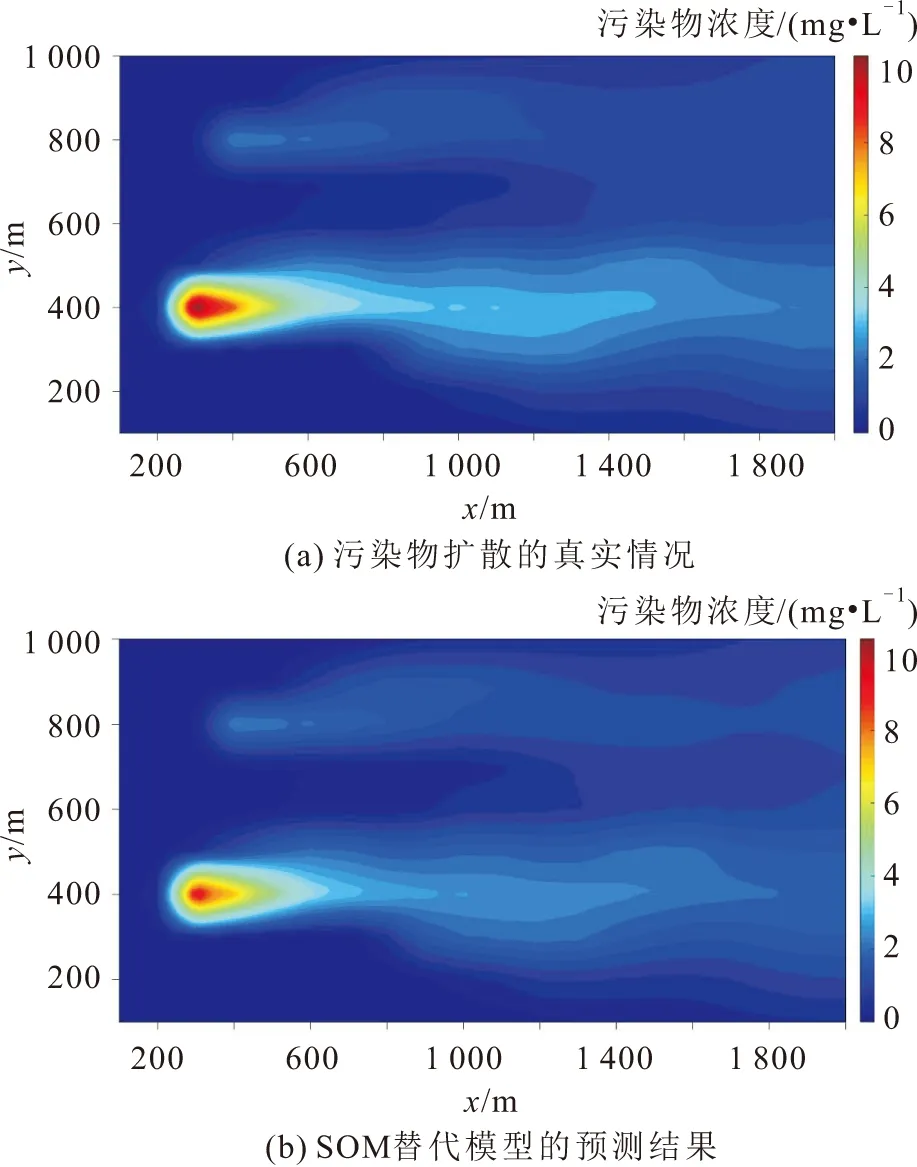
图8 第400 d污染物扩散的污染羽形态分布Fig.8 Contours of contaminant concentrations on the 400th day

由图8可见，两个污染羽在形状上较为接近，接近地下水污染源S1位置处SOM替代模型的预测值(与图7的反演结果一致)。

3 结论与建议

(1) 基于自组织映射(SOM)算法构建地下水中污染物迁移模型的替代模型(简称SOM替代模型)，通过数值算例针对SOM样本数目和SOM神经元数目进行SOM替代模型的训练，最终得到能够准确地表征地下水污染源强信息和观测数据之间联系的最优SOM替代模型。

(2) 经过训练得到基于SOM的最优替代模型后，无需在后续识别过程中再运行原始模拟模型，而传统的模拟优化方法则需要反复多次调用原始模拟模型，直到目标函数达到预设范围，从而得到满意的识别结果，而且调用次数远超过用来构建SOM替代模型所需的训练样本数。

(3) 通过对考虑观测误差和未知抽水井影响下基于SOM替代模型的地下水污染溯源识别结果的鲁棒性进行分析，结果表明：从无误差到20%的观测误差水平，表征地下水污染溯源识别精度的NAEE值从4.22%增至6.46%，表明观测误差的引入对识别结果的影响不大；另一方面，当存在未知抽水井时，从无误差到20%的观测误差水平，NAEE值由4.22%增至8.31%，表明生成SOM样本的概念模型对SOM替代模型的影响更大。

(4) 后续研究可考虑场地渗透系数场不确定性对地下水污染溯源识别结果的影响，以及与其他方法相结合的SOM替代模型用于实现场地渗透系数场的反演推估。