复杂软土盾构隧道纵向抗震分析
2021-06-08郭正阳梁建文李东桥王智恺吴泽群
郭正阳,刘 瑜,梁建文,李东桥,王智恺,吴泽群
(1.天津滨海新区轨道交通投资发展有限公司,天津 300459;2.中国铁路设计集团有限公司,天津 300142;3.天津大学建筑工程学院,天津 300350)
0 引言
近年来,随着我国地铁建设快速发展,地下隧道抗震问题受到越来越多的关注,地下结构的抗震分析,已经成为各类地下工程设计的必要环节。
目前,地下结构纵向抗震分析多采用反应位移法[1-4]。反应位移法认为地下结构在地震时的纵向反应主要取决于周围土层的变形,将土的变形情况通过弹簧的形式加到隧道上,以弹性地基梁模拟盾构隧道,计算隧道内力和变形,该方法计算量较小,能够考虑不同方向地震波的影响。
需要指出的是,盾构隧道是管环由接头(螺栓)连接起来的不连续体,其刚度也是不连续的,接头处的刚度一般比管环本身的刚度要小,为此,在进行盾构隧道的纵向抗震分析时,应该充分考虑管环间接头的影响。
目前,盾构隧道多通过对隧道整体刚度进行调整来考虑管环间接头对整体刚度的影响,但这种方法并不能反映出地震作用下隧道与接头反应的差异。为此,本文采用6个方向环间弹簧来模拟接头效应,刚度系数由螺栓实际连接情况确定。
另外,《城市轨道交通结构抗震设计规范》[5]规定,隧道结构纵向地震反应时的验算,可分别根据隧道结构纵向和横向水平方向地震动的结构反应进行抗震验算。《城市轨道交通结构抗震设计规范》[5]同时指出,纵向地震反应分析,应综合考虑纵向和横向水平向地震动的耦联结果,对结构进行纵向和横向验算,但两个方向地震动的耦联方式有待进一步深入研究,且两个方向地震响应最大值一般情况下不可能同时发生。
针对上述耦联问题,本文提出一个同时考虑纵向和横向水平方向地震动的方法,以纵向和横向水平方向地震动幅值比为1/0.85或0.85/1来考虑纵向和横向水平方向地震动之间的耦联效应,进行隧道纵向抗震计算。
由此,本文利用ABAQUS有限元软件,结合天津Z2线盾构隧道工程,建立三维梁-弹簧模型。总结和归纳盾构隧道环间弹簧的计算方法,采用弹簧模拟管环间的螺栓连接。采用粘弹性边界,结合等效节点力地震动输入方法,进行两个典型纵断面的非线性地震响应分析,采用等效线性化方法考虑土体的非线性。文中分别计算了在安评波小震、中震和大震作用下的隧道内力和变形,以期为天津Z2盾构隧道抗震设计提供参考。
1 模型
1.1 模型建立
盾构隧道在地震作用时的响应,主要由周边土层的相对变形支配。依据初勘报告和地震安全性评价报告,按照隧道所处穿越软夹层、上软下硬等复杂土层条件等基本原则,选取两个典型纵断面作为分析对象。
基于ABAQUS有限元分析软件,盾构隧道采用三维梁单元进行模拟。对于盾构隧道,梁单元长度应按盾构环的长度确定,模型总长度不宜小于地层变形波长或取全长,因此根据场地条件,确定两个模型长度均为630 m。
由于每个盾构环长度为1.5 m,在每环中间设置地基弹簧,梁单元长度取0.75 m。梁单元采用ABAQUS三维梁单元。梁单元截面依据实际隧道直径取6.25 m,壁厚为0.35 m。
考虑盾构环间纵缝的影响,梁单元在纵缝处断开,通过6个方向的环间弹簧连接。土-结构相互作用用土弹簧来模拟。
1.2 材料本构确定
盾构管片混凝土的强度等级为C50。环间螺栓接头采用5.8级的M30螺栓,具体材料参数取值如表1所示。

表1 混凝土及螺栓材料参数Table 1 Material parameters
1.3 土弹簧刚度系数确定
规范[5-7]中给出了地基土弹簧计算方法,地基弹簧刚度按照下面公式计算:
kt=KLW
(1)
(2)
式中:K为基床系数(N/m3);L为地基的集中弹簧间距(m);W为隧道横向平均宽度或直径(m),地基土的基床系数通过现行国家标准《核电厂抗震设计规范》[7]采用下式确定:
Kt=3G
(3)
(4)
式中:G为与土层最大应变幅值相应的地基土的剪切模量(GPa)。
土弹簧刚度非线性参数如表2和表3所列。
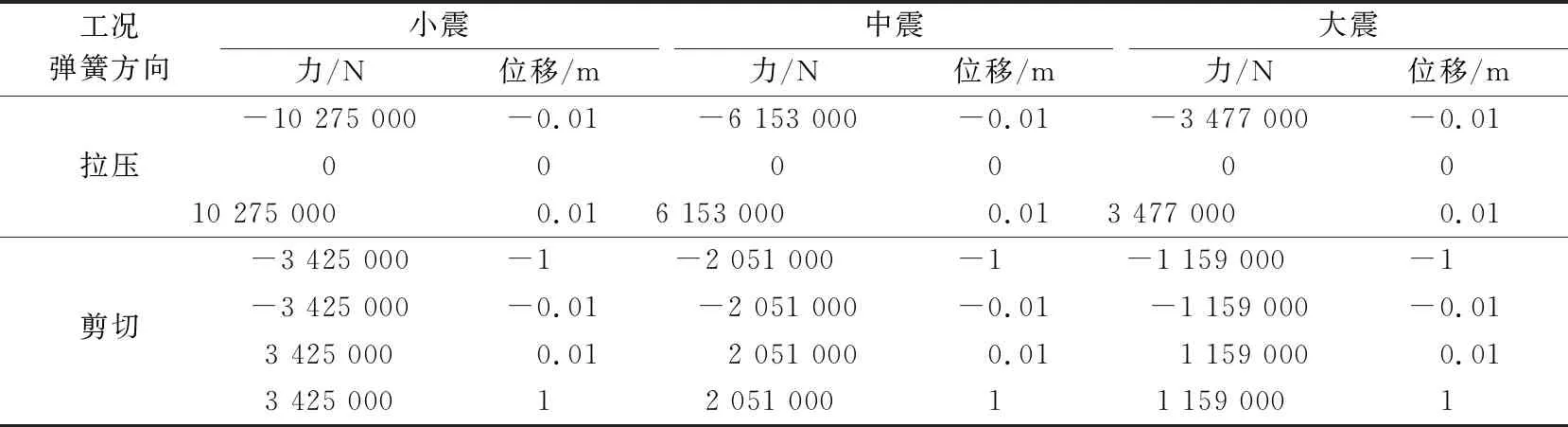
表2 纵断面1地基弹簧刚度非线性参数Table 2 Nonlinear parameters of foundation spring stiffness for longitudinal section 1
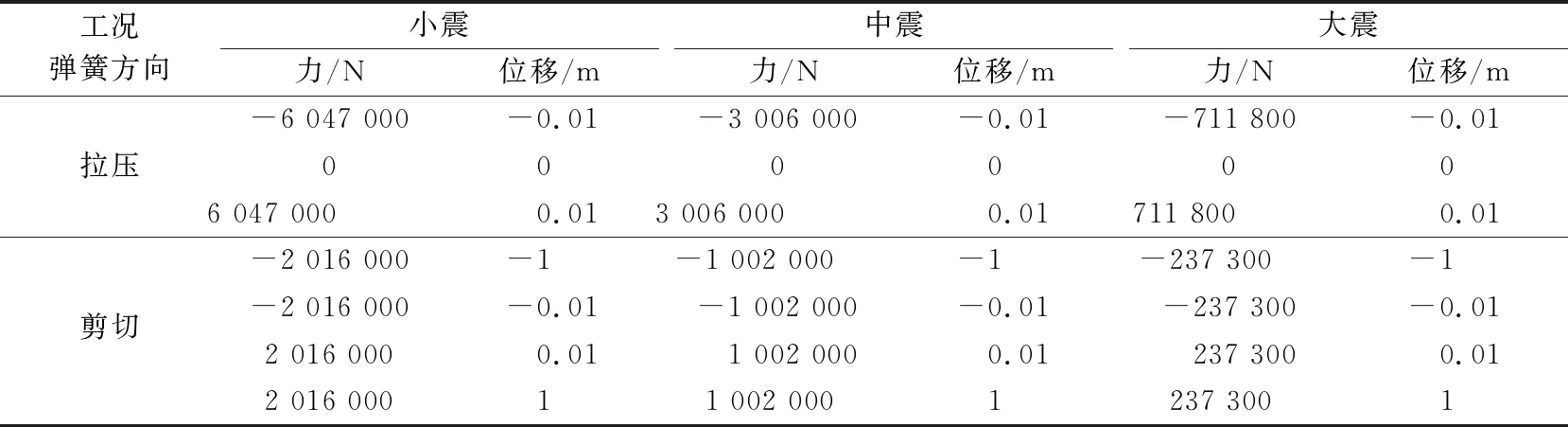
表3 纵断面2地基弹簧刚度非线性参数Table 3 Nonlinear parameters of foundation spring stiffness for longitudinal section 2
1.4 环间弹簧刚度计算
目前的规范以及文献常将隧道作为等效刚度模型,该模型是通过将整体隧道的刚度做一定的调整,来考虑由于管片之间的接头对整体刚度的影响。等效刚度按照衬砌的材料以及尺寸确定,一般按照变形量相同的原则进行等效计算,将纵向圆环单元按平面应变问题处理,可获得其等效弹性抗拉、抗压和抗弯刚度[8]。这种处理方式在一定程度上使反应位移法的计算变得简便,但也降低了内力计算结果的准确性,不能够反映接头部位与隧道管环部位的差别。
为了解决这一问题,本文通过搜集相关计算隧道环间弹簧的文献和资料,总结出了三维梁单元模拟隧道时,六个方向的环间弹簧计算方法。
本文模拟的三维梁单元模型环间弹簧有6个方向的刚度:X方向为拉压弹簧、Y和Z方向为剪切弹簧,绕X轴转动方向为扭转弹簧、绕Y轴和Z轴转动方向为弯曲弹簧。
(1)X方向拉压弹簧
抗拉刚度:Kt=nEA/l;抗压刚度:Kc=EcAc/l。其中,E为螺栓弹性模量(GPa),A为螺栓横截面积(m2);Ec为混凝土弹性模量(GPa);Ac为混凝土受压面积(m2);l为环间螺栓长度(m);管环间有16个螺栓,n=16。
抗拉刚度:Kt=3.56×109N/m
抗压刚度:Kc=4.47×1011N/m
(2)Y方向及Z方向剪切弹簧
依据文献[9],抗剪刚度:
Ks=16×2.332 2×1010=3.73×1011N/m
(3)绕X轴转动方向扭转弹簧
不考虑螺栓的扭转刚度,Kθx=0
(4)绕Y轴及Z轴转动方向弯曲弹簧
按照《盾构隧道管片设计》[10]纵向等效刚度方法计算纵断面方向上的转动弹簧系数:
(5)
(6)
这里,φ满足下式:
(7)
式中:φ中和轴位置的角度;Es管片主体弹性模量(GPa);Is管片主体断面惯性矩(m4);ls管片宽度(m);M为作用隧道纵断面弯矩(N·m)。
求得抗弯刚度:
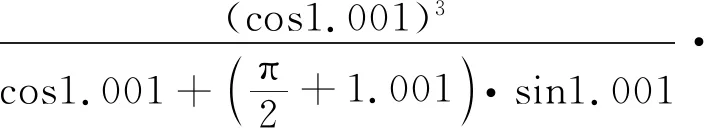
4.49×1010(N·m/rad)
(8)
1.5 施加位移计算
施加在地基土弹簧端部的位移,依据规范[5]来确定,具体公式如下:
(9)
(10)
L1=TSVSD
(11)
L2=TSVSDB
(12)
式中:u(x,y)为坐标处地震时的地层水平位移(m);umax(y)为地震时深度y处土层的水平峰值位移(m);L为地层变形的波长,即强迫位移的波长(m);L1为表面地层变形的波长(m);L2为基岩变形的波长(m);VSD为表面地层的平均剪切波速(m/s);VSDB为基岩的平均剪切波速(m/s);Ts为考虑地层地震应变水平的地层场地特征周期(s)。
需要指出的是,式中的umax(y)通过建立二维地震自由场的时程分析模型[11-12]求得。模型以大型通用有限元软件ABAQUS为平台,根据工程场地勘察报告中土层分布情况和参数建立所选断面自由场模型。在模型底部和两侧施加黏弹性边界[13],该边界可以等效为按边界节点分布的并联弹簧-阻尼器系统,阻尼器吸收边界处散射波能量,弹簧模拟远域土的弹性恢复能力,近似满足无穷远辐射条件。模型采用等效结点力方法实现地震动的输入,用自行编制的Python 程序获得自由场地震响应,然后将自由场地震响应换算为等效节点力施加到黏弹性边界,从而实现模型的地震动输入。地震动垂直从基岩面入射。采用等效线性化方法考虑土体材料的非线性,即通过迭代计算剪切模量和阻尼比模拟土的非线性变化,从而将非线性求解过程等效线性化[11-12,14],本文基于 Python 语言编写相关程序,使整个迭代过程在 ABAQUS 中自动运行,无需人工干预。
模型计算完成后,提取与隧道轴线埋深相同位置的土层的位移时程,求得所有节点在整个时程的最大幅值作为在该地震激励下深度y处土层的水平峰值位移,将提取计算的umax(y)代入公式中,即可求得不同坐标处地震时的地层水平位移。其中,纵断面1见图1,基岩的安评地震动见图2,建立的二维自由场模型如图3和图4,土的非线性参数见文献[15]。
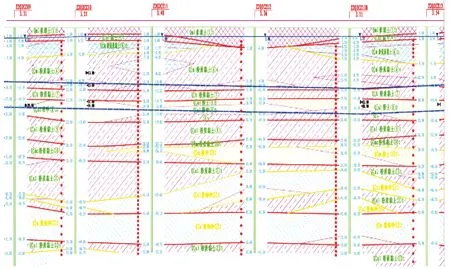
图1 隧道及土层纵断面剖面图Fig.1 Profile of longitudinal section of tunnel and soil layer
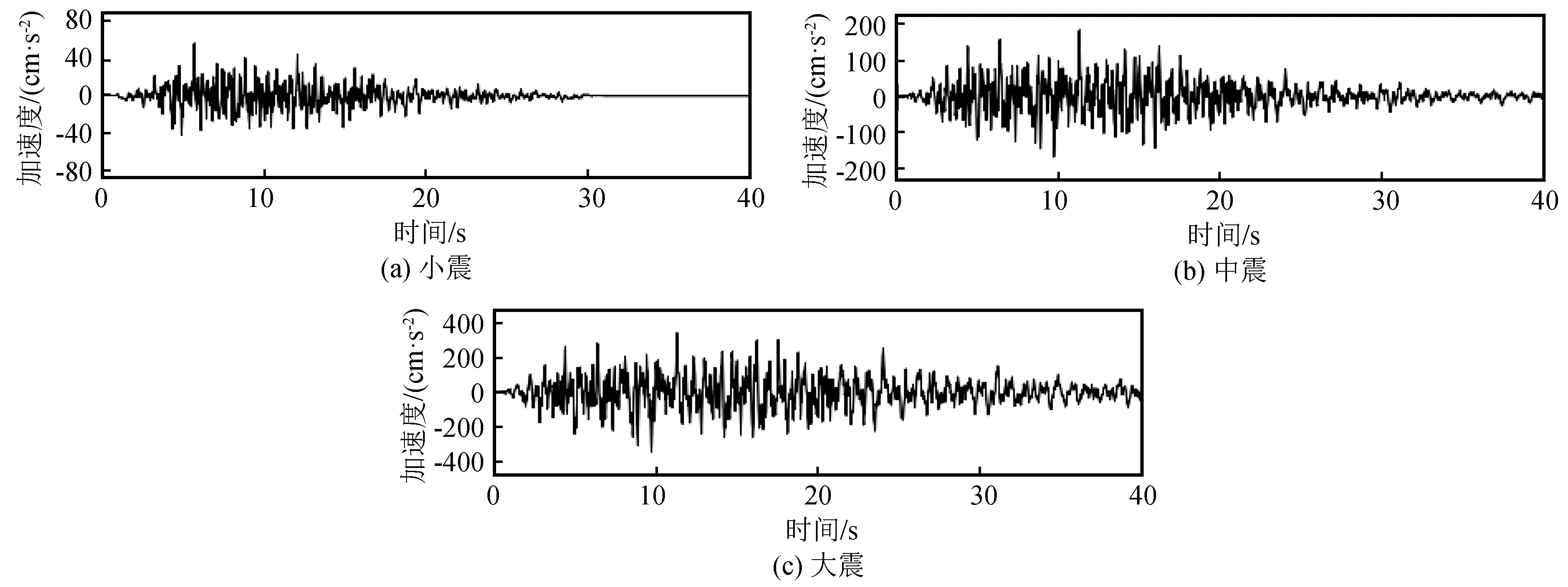
图2 基岩安评地震动时程曲线Fig.2 Time history curves of bedrock ground motions

图3 二维有限元模型图Fig.3 Two-dimensional finite element model diagram

图4 模型网格划分与隧道轴线位置Fig.4 Model meshing and tunnel axis position
为考虑纵向和横向水平地震动之间的耦联效应,根据强震观测记录统计分析[16],两个水平方向地震动加速度最大值约为1/0.85,将地震响应位移分别按照轴向和横向分别为1/0.85和0.85/1的比例施加在地基土弹簧端部。
2 结果分析
将上节求得的地层水平位移分4个工况对梁单元模型施加位移:(Ⅰ) 以umax(y)为幅值在横向施加正弦位移;(Ⅱ) 以umax(y)为幅值在横向、同时以0.85umax(y)为幅值在轴向施加正弦位移;(Ⅲ) 以umax(y)为幅值在轴向、同时以0.85umax(y)为幅值在横向施加正弦位移;(Ⅳ) 以umax(y)为幅值在轴向施加正弦位移。
通过对计算结果进行提取、汇总,可得两个典型纵断面在各种工况下结构的内力峰值和最大接头张开量,见表4和表5。
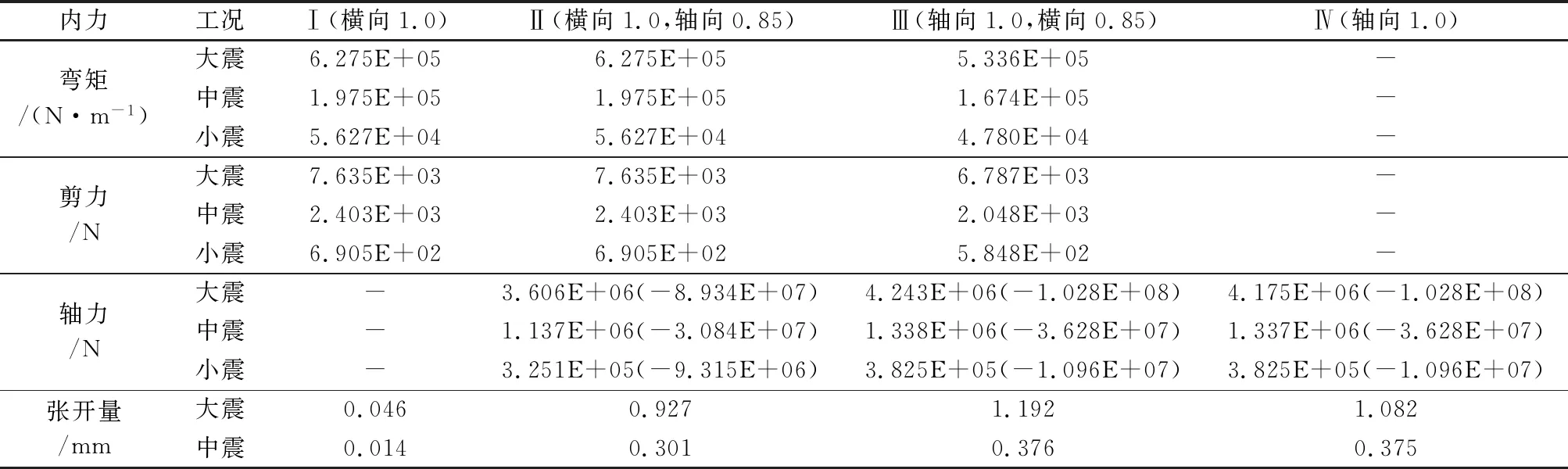
表4 结构响应峰值图 (纵断面1)Table 4 Structure response peak (longitudinal section 1)

表5 结构响应峰值图 (纵断面2)Table 5 Structure response peak (longitudinal section 2)
可以看出,工况Ⅱ与Ⅰ相比,弯矩、剪力峰值基本不变;工况Ⅱ与工况Ⅲ相比,弯矩和剪力峰值为1/0.85。由此说明,土层横向位移对结构的弯矩和剪力起控制作用,土层横向位移与盾构隧道的剪力峰值和弯矩峰值成正相关关系。
工况Ⅲ与Ⅳ相比,轴力峰值基本不变;工况Ⅱ与工况Ⅲ相比,轴力峰值为0.85/1。由此说明,土层轴向位移对结构的轴力起控制作用,土层轴向位移与盾构隧道的轴力峰值成正相关关系。同时也说明,对于接头拉压异性的梁-弹簧计算模型,弹性地基梁理论依旧适用。
可以看出,接头张开量在工况III达到最大,工况Ⅳ次之,工况Ⅱ排序第三,工况Ⅰ最小,这说明,土层轴向位移对接头张开量起控制作用,同时说明,考虑纵向和横向水平地震动之间的耦联效应是必要的。
3 结语
以天津市Z2线盾构隧道为例,采用反应位移法进行隧道纵向抗震分析。
提出一种考虑轴向和横向水平地震动的耦联效应的方法。研究表明,土层横向位移对结构的弯矩和剪力起控制作用,土层轴向位移对结构的轴力起控制作用;而就接头张开量而言,考虑纵向和横向水平地震动之间的耦联效应是必要的。
根据隧道螺栓实际连接情况,直接计算环间弹簧刚度,相较于常见的等效刚度模型来说,更加符合实际情况,计算精度也更高。
