基于FP微阵列的压缩感知光谱重建研究

吴笑男，张 瑞，王志斌，陈壮壮

（中北大学 理学院 山西省光电信息与仪器工程技术研究中心，山西 太原 030051）

引言

随着光学信息获取技术的进一步发展，各类光学信息获取技术在探测方面集成，可实现不同目标信息的同时获取。光谱成像技术是一种多维成像的新型技术，由成像技术与光谱分析技术二者相结合形成，可以同时获得目标场景的光谱与空间二维信息。因此，光谱成像技术被广泛应用于各个领域。根据分光方式不同，光谱成像技术主要分为以棱镜、光栅作为分光元件的色散型光谱成像技术，滤光片型光谱成像技术以及干涉型光谱成像又叫做傅里叶变换光谱成像技术。根据扫描方式不同，光谱成像技术主要分为摆扫型、推扫型和凝视型[1]。随着科技的不断发展，人们对光谱成像技术的要求也越来越高，高空间、高光谱分辨率、高光通量、高信噪比以及高效率的存储和传输等要求为光谱成像技术提出了新的挑战。尤其是星载光谱成像技术，多采用滤光片阵列[2]、光栅和傅里叶分光方式[3]，但滤光片阵列型光谱通道数有限且光谱分辨率低，光栅型光通量低，傅里叶型空间分辨率低。在我国，对于光谱调制成像系统的研究虽起步较晚，但在不断研究与探索下，也取得了突出成果。西安交通大学李杰等研制出基于静态傅里叶变换偏振光谱成像系统[4-5]，运用强度调制模块与沃拉斯顿棱镜对光谱进行调制，实现对光谱信息及图像的同时获取。中科院长春光机所研制出多谱段偏振成像仪，该系统应用于云和大气气溶胶检测，可以识别大气检测过程中的云干扰，提高反演信息的精确度。北京航空航天大学的张颖、赵慧洁等人设计了多谱段成像系统[6]，利用双液晶可变相位延迟器（liquid crystal variable retarder，LCVR）进行相位调制及旋转滤光片分光，通过对入射光的相位延迟量进行调制，从而得到目标的光谱信息。

随着压缩感知技术[7-9]发展，光谱成像与其进行结合，产生压缩感知光谱成像技术[10-12]。其中压缩感知实现了信号的采集和压缩同时进行，避免了繁重数据的采集以及大量采样数据的浪费，从而减轻采集任务。不同于传统压缩的是，压缩感知直接采集压缩后的有效数据，通过一定的压缩比，从少量的数据中捕获和恢复原始信号，不仅节约资源，提高效率，而且能够精确地恢复原始信号，这也是压缩感知的核心思想。2006年，杜克大学的Brady等人运用二维编码模板结合计算机仿真提出了压缩感知光谱成像技术[13]。2016年，Johann等人模拟和研究了多路复用中波红外成像仪图像计算光谱成像技术[14]。2018年，Michael等人提出一种新的光谱成像方法，通过在普通的数码相机上安装一个色散扩散器和一个基于压缩传感器的数字处理算法，将普通的数码相机转换为快照光谱成像仪，实现了快照光谱成像仪的小型化、轻量化设计[15]。但现有压缩感知光谱成像无法同时实现高通量、高光谱分辨率、高空间分辨率。

本文针对星载扫描特点及现有光谱成像存在的问题，将光谱成像技术与压缩感知相结合[16]，提出了一种基于法布里珀罗（Fabry-Perot，FP）微阵列的快速扫描光谱成像系统。在确保高光谱、高空间分辨率，以及高光通量的前提下，实现了光谱信息的快速、高效采集。

1 基本原理

1.1 FP微阵列压缩感知光谱成像基本原理

虽然压缩感知光谱成像得到很大发展，但目前多采用编码孔径方式[17-19]，且需要独立分光元件，导致光通量低、体积大；另外一种典型方式是基于光谱调制的压缩感知光谱成像[20-21]，光谱调制多采用FP和电光调制，但无法同时实现高通量、高光谱分辨率、高空间分辨率。因此，传统光谱成像和普通压缩感知光谱成像存在低光谱分辨率或是低空间分辨率的缺点。我们利用卫星扫描特点，结合压缩感知技术，设计了基于FP微阵列的压缩感知扫描光谱成像方式，如图1所示。

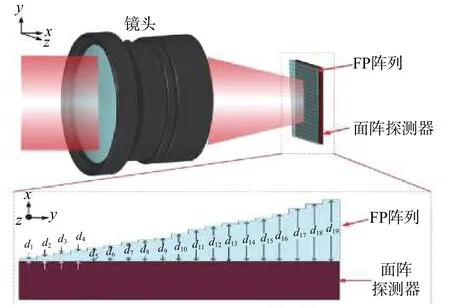
图1 快速扫描光谱成像系统设计图Fig.1 Schematic diagram of rapid scan spectral imaging system

该结构由一个1×19的FP阵列、一个面阵探测器以及一个镜头组成，卫星飞行扫描方向沿y轴，其中每两个反射镜之间有不同的间隙d。平行光沿x轴进入镜头，通过镜头汇聚到FP阵列上对入射光信号进行调制，然后由面阵探测器收集。利用两步迭代阈值收缩算法(two-step iterative shrinkage/thresholding，TWIST)可以恢复原始光谱信息。面阵探测器通过收集19个调制后的光谱数据，经过适当的压缩感知（compressed sensing，CS）算法，重建得到上百个原始光谱数据，扫描系统与快照系统不同，快照系统普遍应用于凝视环境下的成像，而扫描系统可用于卫星扫描成像。与传统凝视型成像系统相比，由于我们的成像系统沿y轴进行动态扫描，系统会对同一位置的光谱信息进行多次扫描，意味着该设计具有更高的信噪比和光通量，可为微光条件下光谱成像探测提供帮助。此外，由于利用了压缩感知框架，可以重建高于一个数量级以上的光谱波段，相比于其他基于多孔径方法的相机[22-24]，具有很大优势。

1.2 压缩感知原理

压缩感知框架由稀疏信号模型、适当的测量矩阵设计以及恰当的重建算法[25]3部分组成。一般情况下，我们认为，当信号本身具有稀疏性或在某些变换域中可满足一定的稀疏性时，可以将高维的信号通过与测量矩阵相乘投影为低维的信号，也就是说此信号是可压缩的。变换域的选择尤为重要，它与信号的稀疏性紧密相关，选择好的变换域，可使信号获得较优的稀疏表示，从而使得重建信息更加精确。压缩感知理论提供了一种从M个不同的测量信号中还原出N个信号的技术，其中N>>M。当信号满足一定稀疏性时，并且使用适合的传感矩阵时，可以实现这种技术。在此，我们用矢量f表示原始光谱信息，用矢量g表示测量信号。那么，压缩感知过程可以表示为

式中：Θ表示传感矩阵，且 Θ∈BM×N；Φ为测量矩阵；Ψ为稀疏矩阵；传感矩阵包括稀疏矩阵和测量矩阵，测量矩阵和稀疏变换基互不相干；θ表示稀疏变换后的系数。

压缩感知过程如图2所示，其中θ为f在Ψ 域中的稀疏表示。为了重建原始信号，开发了许多算法。常用的算法为TWIST算法，通过解决最优解问题来估计原始信号f：

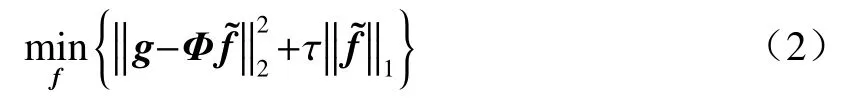
图2 压缩感知数学模型Fig.2 Mathematical model of compressed sensing

2 仿真及数据分析

2.1 FP调制器工作原理

由于星载扫描实际需在真空条件下，实验操作难以实现，我们用一个改进的FP调制器代替设计的FP微阵列对输入信号进行调制。FP两个反射镜之间的距离d对应FP阵列中不同的高度，以此来验证FP微阵列的可行性。FP调制器由两个平行的平面反射镜组成。理想FP调制器的透射率由（3）式得出：

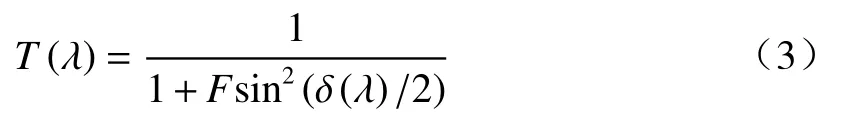
式中δ（λ）是入射光信号之间的相位差，等于：

式中：λ是波长；n是两个FP反射镜之间的介质折射率；i是光信号的入射角；参数F由（5）式给出：

式中R为FP两个平面反射镜的反射率。FP调制腔对入射光谱信息进行调制，输出强度由传感器接收。通过改变d的值，我们会得到K个不同的调制光谱。

一般来说，我们希望光谱响应具有相对较窄的峰值，这样可以方便获得对(4)式中不相干特性的测量；另一方面，他们应该足够宽，以便通过测量来充分感知波长。在压缩感知中，传输峰的最优集合将使相应的传感矩阵 Φ具有最低的相干参数μ。通过模拟传感矩阵，根据方程（3），以空气为介质，在FP反射镜之间，发现了最优压缩感知条件（即具有最低的相干参数μ）。当反射镜反射率为0.8时，得以实现最优条件[20]。

当平面镜反射率为0.8时，波长在400 nm～700 nm范围内，FP可分辨的最小波长间隔为

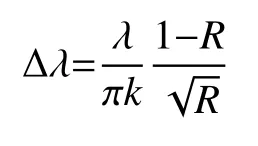
由上式可知，R为0.8，λ在400 nm～700 nm之间，由于FP的腔长h最大约为100 μm，从而使得干涉条纹的级数k的数量级约为103，此时FP可分辨的最小波长间隔约在0.02 nm～0.05 nm之间，所以入射波长在400 nm～700 nm的范围内时，可以实现光谱通道达到700个的要求。

如图3所示，光信号进入FP调制腔进行调制，通过调节压电驱动器，我们可以控制FP两个反射镜之间的距离。调制后的信号经过一个汇聚透镜后进入接收器中。该过程重复K次，由于FP腔宽度d不断变化，从而使每次测量得到不同的光谱响应。在本文中，K=19。图4显示了两个不同的具有代表性的光谱响应。

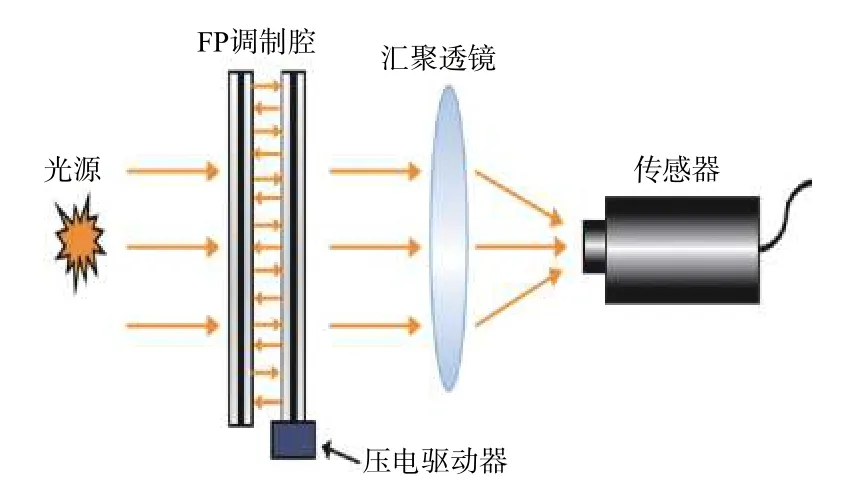
图3 FP调制器装置图Fig.3 Device diagram of FP modulator

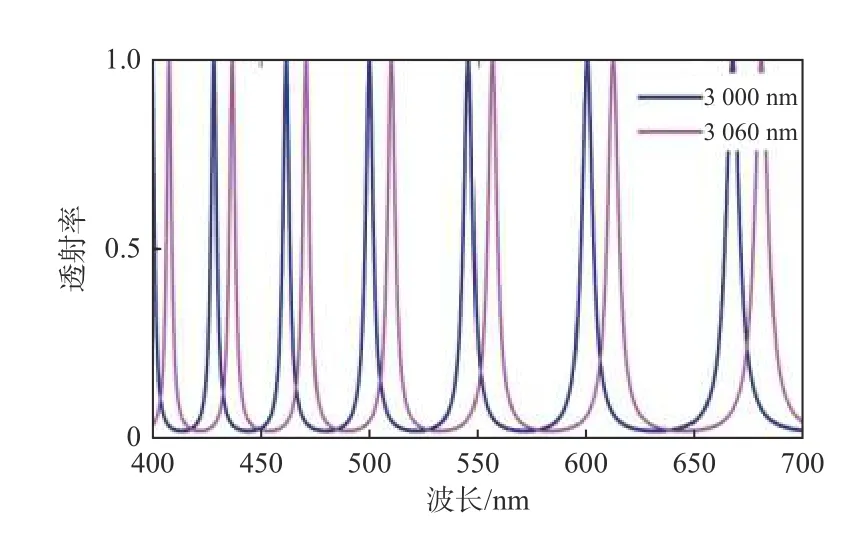
图4 当FP反射镜反射率为0.8时FP调制器两种不同的光谱响应Fig.4 Two different spectral responses of FP modulator when reflectivity of FP reflector is 0.8

2.2 调制光谱压缩过程

上文提到压缩感知由稀疏矩阵、测量矩阵、重建算法3部分构成。图3所示的FP调制腔对输入信号起到调制作用，也就相当于对输入信号进行稀疏表示。接下来的工作是设计测量矩阵，测量矩阵是信号压缩过程的核心，它直接影响信号重构的精度。因此，要实现从低维信号中重构出高维信号，需要对传感矩阵有一定的约束条件。由Candes和Tao提出并证明了RIP（受限等距性质）约束条件[18]。传感矩阵在满足RIP条件的同时，测量矩阵 Φ要与稀疏变换基Ψ 尽量不相干。目前常用的测量矩阵有高斯随机矩阵、二值随机矩阵、局部傅里叶随机矩阵、结构化随机矩阵等。在本文中，我们给出一个FP调制系统透射的例子，通过模拟改变压电驱动器来改变两个平面反射镜之间的距离，选取了19个不同的光谱调制作为测量矩阵[17]。图5表示了测量矩阵的可视化图形，每一行表示不同光谱调制的透射强度。根据（1）式，利用测量矩阵得到压缩后的测量信号g。

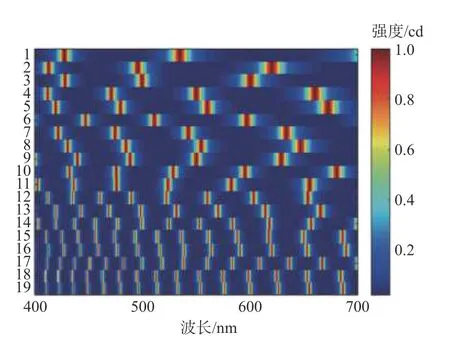
图5 19个不同的光谱调制的透射实例图Fig.5 Transmission instance diagram of 19 different spectral modulations

2.3 压缩光谱重建

光谱重建是对方程（2）的求解过程。由于测量信号g的 维度远小于原始信号f的维度，所以该求解问题是欠定的，因此原始光谱信号的重构问题可以表示为优化求解问题[26]。Candes[27]等人证明该优化问题可以表示为l0范数最优化问题，但是l0范数问题是非凸的，很难求出解。因此，我们把它转换为凸优化问题，也就是转化为l1范数最优化问题，l0范数优化和l1范数优化在一定程度上是等价的。常用的几种信号重构算法包括：贪婪算法、迭代阈值法以及最小化全变分法。本文使用TWIST两步迭代算法重构信号。

由于某种程度上，迭代加权收缩算法(IRS)和迭代阈值收缩算法(IST)的收敛速度都不理想，Josh M.Bioucas- Dias等人将两者结合，提出了两步迭代阈值收缩算法（TWIST）[28]。TWIST算法的迭代值与之前两步迭代所得的估计值有关，其算法更新迭代过程如（6）式：

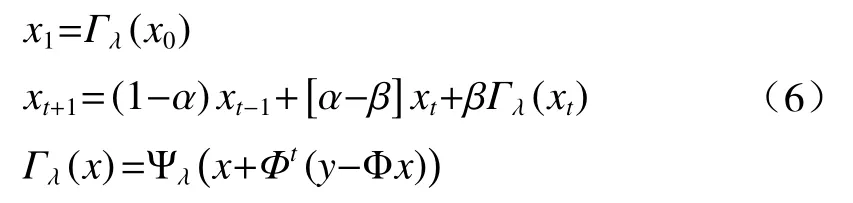
式中：t≥1；x0是初始值；α和β为算法的参数；Γλ为软收缩阈值函数；ψλ为去噪软阈值函数。由该式可以看出xt+1由xt和xt−1共同决定[20]。

TWIST算法将IST和IRS算法的优点相结合，既能保证收敛速度，又可以在噪声环境中高质量地重构信号。以632.8 nm红色激光和532 nm绿色激光为例，验证实验的可行性。

2.4 仿真数据分析

首先用标准光栅光谱仪测量两个激光的叠加光谱，如图6所示。然后用通过仿真测量矩阵采集到的数值进行重构。图7显示了两个激光的重构光谱，通过与光栅光谱仪测得的光谱相比较，可以发现，在400 nm～700 nm的范围内，仅从19个测量数据中重建了700个光谱数据，压缩比约为37∶1。重构光谱与用光栅光谱仪测量的光谱之间的均方误差（mean square error，MSE）为0.002。

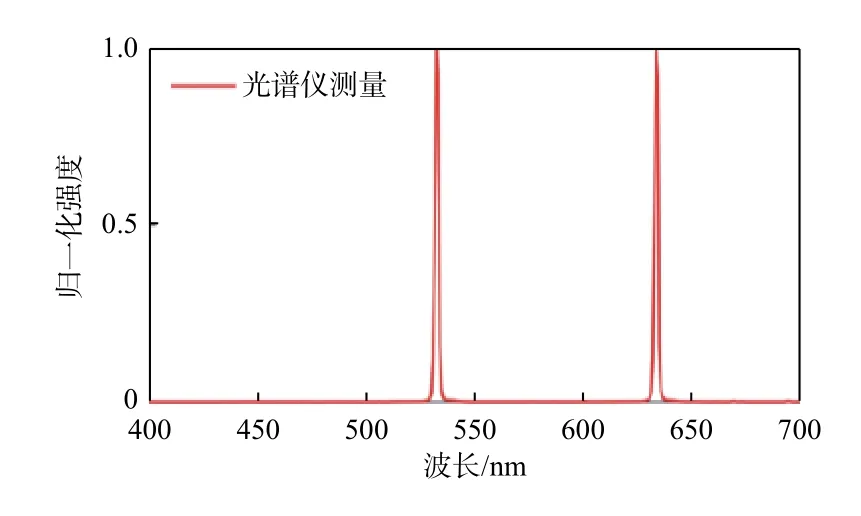
图6 标准光栅光谱仪测得的红绿激光叠加光谱Fig.6 Red-green laser superposition spectrum measured by standard grating spectrometer

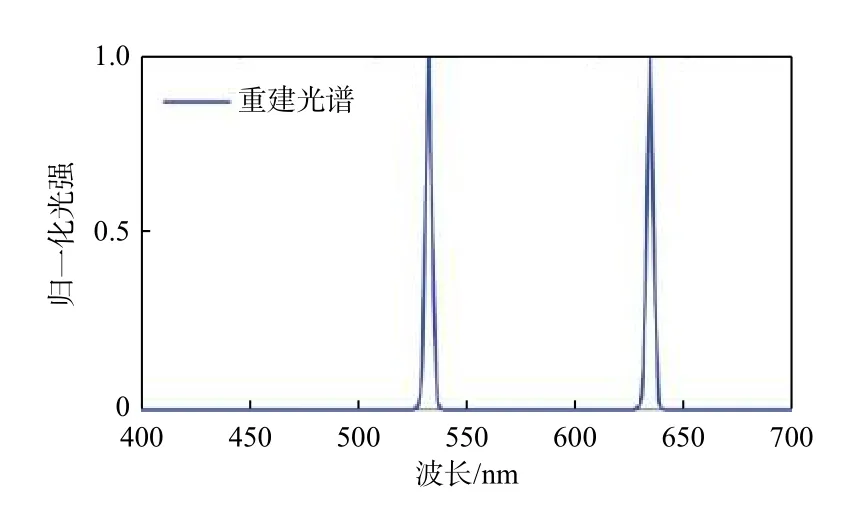
图7 压缩感知重构光谱Fig.7 Compressed sensing reconstruction spectrum

3 实验部分

3.1 实验装置

FP调制系统的实验装置如图8所示，在该系统中，光谱信号通过FP调制腔，FP调制腔由两个特别制造的反射镜构成。该反射镜的反射率约为0.8。为了控制两面反射镜之间的距离，在其中一个镜子下面加了压电驱动器。使用的驱动器为PI公司的P-611.1线性压电陶瓷定位系统，行程为1 μm～100 μm，分辨率可达0.2 nm。光信号经过FP调制腔进行调制，经过调制的光谱信号由传感器接收。

图8 FP光谱调制系统Fig.8 FP spectral modulation system

特别说明的是，由于干涉测量系统是非常敏感的，所以FP反射镜需要小心地平行放置。此外，压电驱动器需控制在几纳米的范围内，才能确保光谱调制的精度和重复性[17]。

3.2 实验结果分析

为了验证仿真数据的准确性，我们进行了实验。首先，用标准光谱仪测得黄蓝两种不同颜色LED点光源的光谱。然后，分别以黄蓝两种不同颜色光源作为入射光信号，经过FP调制器对入射光信号进行调制，用探测器收集FP调制器不同间隙下的光谱响应总强度。此外，利用压缩感知重构算法重建入射光谱，黄蓝两色重建光谱的均方误差（MSE）分别为0.004和0.005。光谱重建结果如图9～图10所示。在400 nm～700 nm的范围内，光谱带的数量为700个，仅从19个测量值中重建出来。如图所示，黄蓝两单色光的重建光谱与标准光谱仪测量光谱之间存在一定的差距，造成此误差的原因主要有两个方面：一方面实验过程中不可避免有一些轻微震动以及噪音，对光谱收集的准确造成了一定的影响；另一方面在测量矩阵的设计上，测量矩阵的选取对重建结果也造成了一定误差，我们会继续优化测量矩阵，来减小重建光谱与标准光谱仪测量光谱之间的差距。

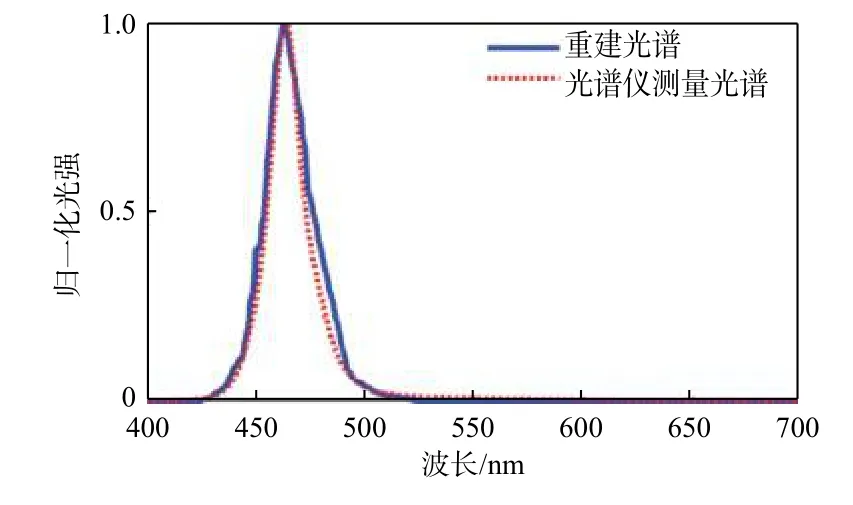
图9 蓝色LED点光源重建光谱与标准光谱仪测量光光谱对比Fig.9 Comparison of reconstructed spectrum of blue LED point light source and measuring light spectrum of standard spectrometer

图10 黄色LED点光源重建光谱与标准光谱仪测量光光谱对比Fig.10 Comparison of reconstructed spectrum of yellow LED point light source and measuring light spectrum of standard spectrometer

4 结论

本文设计了一种新型扫描成像系统，该系统光谱范围为400 nm～700 nm，光谱通道数高达700个，仅从19个测量数据中重建出原始光谱信号，压缩比约为37∶1。仿真激光入射光谱与压缩感知重构光谱进行对比，仿真均方误差（MSE）为0.002。实验反演验证了实验获得的重构光谱与标准光谱仪测得的光谱基本一致，证明了设计的可行性。与传统的光谱扫描系统相比，提出的FP阵列设计以及结合压缩感知光谱重构方法从较小的测量值中恢复原始信号，因此提高了采集速度和光通量，且具有较高的空间分辨率和光谱分辨率，为星载微弱光照环境下的光谱成像提供了便利，具有重要的科学价值和广泛的应用前景。