风力影响下湖泊湍流特征及其对湖泊污染沉积物影响研究

李 燕，顾圣海

(南通和信工程勘测设计院有限公司，江苏 南通 226000)

1 概 述

湖泊的污染程度是生态环境评价的重要指标，而湖泊的水质好坏与水体中悬浮物浓度密切相关。张运林等[1]研究了太湖水体中悬浮物的分布规律与组成成分，并提出悬浮物的浓度是影响水体透明度的关键因素；吴晓东等[2]分析了滆湖中悬浮物的分布情况和其受季节影响的变化规律，其研究显示藻类和湖底泥沙扰动是影响悬浮物浓度的主要原因；高炜程等[3]分析了水体中悬浮物含量的随时空分布改变的差异，建立了悬浮物含量和叶绿素a和总磷浓度的相关关系；高小孟等[4]研究了悬浮物沉降速度与其浓度的关系，总结了悬浮物的动态沉降特征；陈金红等[5]分析了包括叶绿素a、悬浮物浓度和有机物浓度等因素对湖泊的富营养化进行了综合性评价。由此可知，悬浮物浓度是评价水质的重要指标，而风力条件下的湖泊湍流特征则是影响悬浮物浓度中不可忽略的因素。邵宇阳等[6]针对不同程度下的波浪情况计算其雷诺应力，分析了湍流情况与悬浮物扩散之间的关系；钟小燕等[7]研究了流速对湖泊底泥污染物释放的影响；李一平等[8]分析了风速、波流综合切应力和水土接触界面的相关关系；曹志先等[9]建立了湍流猝发与悬浮物沉降及扩散的对应关系模型；周阳等[10]基于风速的变化，比较了不同风速下水体中各离子浓度的变化量。

本文以太湖作为研究对象，探究风速影响下湖泊湍流特征的变化，并评价其变化对湖泊污染沉积物的影响，为水体悬浮物扩散机理研究以及湖泊水质治理提供了科学的依据。

2 区域概况和试验设计

太湖是我国面积第三大的淡水湖，水域总面积为2 338 km2，南北长68.5 km，东西宽34 km，多年平均水深1.89 m。春夏平均风速为4.3 m/s，秋冬平均风速为0.9 m/s。本次研究主要区域位于接近太湖中央的一块区域(N31°12′54″，E120°7′27.65″)。

本次试验在2019年7月24日15∶00至8月4日15∶00进行，采用PH-Ⅱ Handheld手持式气象站在距水面5 m处每5 min测量一次风速，于水底泥面以上10 cm处，水面以下30 cm处分别设置一台ADV Ocean和一台ADV，频率均为10 Hz，两台浊度仪(OBS3A)被放置在距离水底泥面以上5 cm处和水面以下50 cm处，每3 min监测一次，同时记录了包括风向、采样时间、水位等数据。

3 数据处理方法

3.1 水-土界面切应力

1) 由波浪引起的切应力。在水-土界面水颗粒质点沿近圆形轨道运动，然而随着水深的减小，质点将逐渐演化成沿直线运动，故在接近底面的波浪质点的最大速度可由下式计算：

(1)

(2)

式中：uw、h、Hs、Ts、Ls分别为近底面最大波动轨道速度(m/s)、水深(m)、有效波的波高(m)、周期(s)与波长(m)，该值可通过多次迭代得到。

波切应力则可以通过下式确定：

(3)

式中：τw、ρ分别为波切应力(N/m2)、水体密度(kg/m3)；波摩擦系数fw的计算公式为：

fw=exp[5.2(Aδ/Ks)-0.19-6.01]

fw,max=0.3(若Aδ/Ks≤1.57)

(4)

式中：Ks为粗糙高度，本文中取0.000 2 m；Aδ为近底面波浪质点振幅，由下式确定：

(5)

2) 由湖流引起的切应力。该切应力可由下式确定：

(6)

(7)

3) 波流综合切应力。综合切应力可由下式确定：

τcw=τw+τc

(8)

(9)

式中：τcw、β、α分别为波流综合切应力、波和流的方向。

3.2 湍流动能

湍流动能(TKE)可由ADV Ocean所测得的流速以下式计算：

(10)

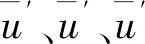
3.3 悬浮物浓度

由于OBS浊度仪只能每3 min监测一次，满足不了数据需求。因此，为了提高数据密度，建立了ADV回声强度(EI)和悬浮物浓度(SSC)之间的关系曲线，见图1。

图1 SSC与EI拟合曲线

4 试验结果分析

4.1 湖底污染沉积物与风速关系

为了研究湖底污染物悬浮沉降与风速之间的关系，以风速为自变量，悬浮物浓度为因变量，建立地层和表层风速与悬浮物浓度之间的拟合曲线。见图2。

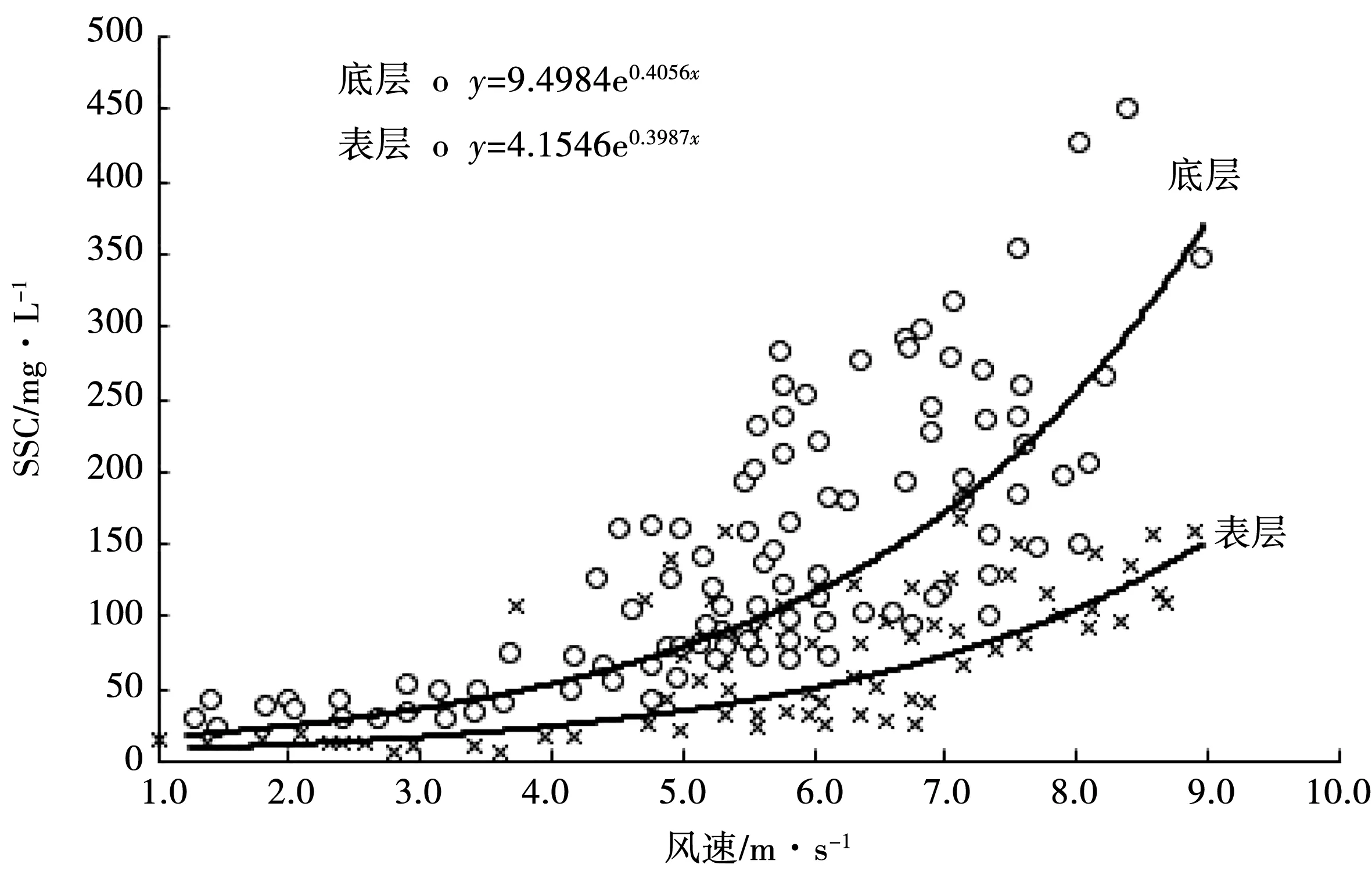
图2 SSC与风速拟合曲线

从图2中可以看出，在风速为3 m/s以下时，底层与表层浓度相差不大，两者变化趋势也基本一致；在风速达到4 m/s后，表层的悬浮物浓度依旧处在一个平缓的上升阶段，底层的浓度则开始呈现出明显的加速上升趋势；在达到5～6 m/s的风速时，底层的悬浮物浓度迅速上升，并且上升的速度也在急剧增长。

从图2中可以看出，其上升趋势基本呈指数形式，此时表层的浓度曲线依旧保持平缓；在风速达到7 m/s时，表层的浓度开始表现出上升加快的趋势，而底层的沉积物已经开始大范围的悬浮，浓度上涨的速度接近峰值；在风速处于8～9 m/s时，底层悬浮物浓度曲线接近竖直线上升，表层的曲线虽然也有上扬，斜率却远小于底层。

从图2中可以看出，底泥起悬的风速临界值大约在4～5 m/s，然而仅观测11 d的数据不能得出准确的结论，因此笔者收集了往年的数据进行了分析，结果见图3。

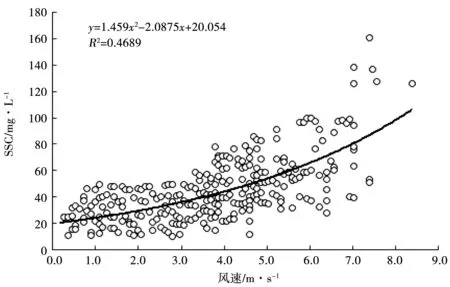
图3 长期SSC与风速拟合曲线

从图3中可以看出，在风速4.5 m/s以下时，曲线基本处于一个平缓的状态，在此之后曲线便进入了加速上升阶段。同时，在4.5 m/s风速以下的阶段，悬浮物浓度都在50 mg/L之下，此时可以认定底泥并未起悬，随着风速的增大到4.5 m/s，湖底沉积物起悬，悬浮物浓度迅速上涨。由此观之，悬浮物浓度与风速呈正相关趋势，并且是一个接近二次多项式的关系，从曲线中可估计临界风速值约为4.5 m/s。

4.2 水-土界面切应力特征

由以上内容可知，悬浮物浓度与风速值密切相关，而风速正是通过影响水流进而影响各类切应力，当切应力达到临界值时，克服了底泥颗粒的自重，因此导致了底泥起悬。因此，试验中测量计算了各类切应力，并研究其和风速以及悬浮物浓度之间的相关关系，具体结果见图4、图5。

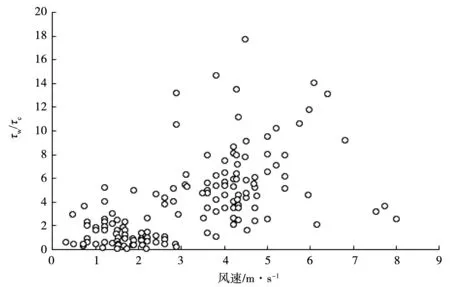
图4 波切应力与流切应力比值和风速的关系

从图4中可以看出，在风速小于2 m/s时，波切应力与流切应力的比值集中在3以下，并且比值小于1的情况时有出现，意味着在风速较小的阶段，流切应力对底泥起悬也有一定的影响；在风速上升到3～4 m/s后，比值基本在1以上，这表明在风速增大以后，流切应力的影响逐渐减小，底泥起悬主要受波切应力的作用；当风速大于4 m/s时，比值均大于1且多集中于2～8之间，随着风速的持续增长，比值集中区域也逐渐增高，在这个阶段，沉积物的悬浮沉降几乎完全依赖于波切应力，流切应力可以忽略不计。考察图4的整体趋势可以明显看出，在湖泊沉积物悬浮的过程主要受波切应力影响，流切应力只在小风速情况下有所作用，在风速增大后，两者比值最大可达到18。由此观之，若要研究水-土界面切应力对沉积物的影响，波切应力应该是主要关注点。

图5 综合切应力与SSC拟合曲线

图5为综合切应力与悬浮物浓度的拟合曲线。由图5可以看出，在综合切应力小于0.1 N/m2时，悬浮物浓度增长缓慢，在切应力超过0.1 N/m2后，悬浮物浓度上升速度加快，说明此时底泥起悬、沉积物颗粒所受切应力克服了重力与浮力的影响。由此观之，0.1 N/m2可以视作底泥起悬的临界切应力。

4.3 湍流动能与沉积物悬浮关系

湍流动能这一参量对底泥起悬的影响也不可忽略，因此本次试验中考察了水底泥面以上5 cm处的湍流动能与悬浮物浓度之间的关系，发现湍流动能与悬浮物浓度变化趋势相关，具体结果见图6。

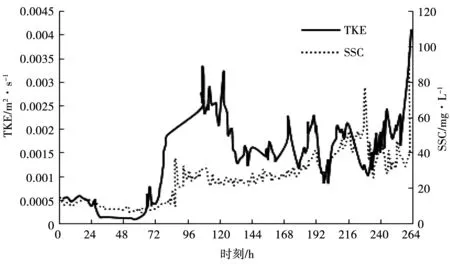
图6 湍流动能和SSC与时间关系

同时，为了进一步探寻湍流动能对底泥起悬的影响，分析了湍流动能与切应力之间的关系，见图7。由图7可知，湍流动能与切应力基本呈正相关关系，并且接近线性相关。因此，随着风速的加快，水-土界面的切应力增加，湍流动能随之增大，最后导致的结果便是底泥起悬、水体悬浮物浓度上升。

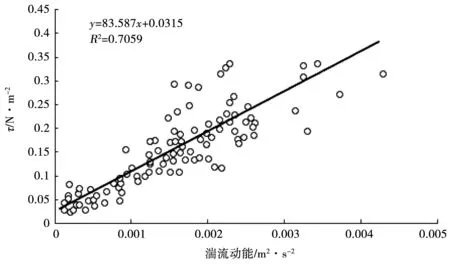
图7 湍流动能与切应力拟合曲线

5 结 论

1) 风速对于水体悬浮物的浓度变化影响较大，随着风速的增大，在达到临界风速时，会造成底泥起悬、悬浮物浓度迅速增大的现象，在本次试验中，临界风速值约为4.5 m/s。

2) 水-土界面切应力直接受风速影响，其中波切应力所受影响更明显，在风速处于较大值时，波切应力可达到流切应力的18倍，这种状态下，底泥起悬主要受波切应力控制。

3) 湍流动能会随着切应力的变化而改变，两者之间呈正相关关系。同时，湍流动能与悬浮物浓度的相关性与此类似。

本次试验研究了风速影响下，湍流特征与湖泊沉积物悬浮沉降的关系，为水环境分析提供了良好的科学依据。