基于思维计划算法优化ELM模型的重庆地区潜在蒸散量分布特征及预测研究

2021-06-08林果果

水利科技与经济 2021年5期

林果果

(重庆市水利电力建筑勘测设计研究院有限公司，重庆 400020)

1 概述

我国是重要的农业生产大国，每年绝对部分用水量均为农业用水。由于近年来干旱现象严重，同时我国水资源较匮乏，人均水资源占有量不及世界平均水平的25%，用水量的缺乏和严重的干旱在一定程度上限制了我国农业产值和经济的发展[1-6]。在有限的水资源前提下，发展节水农业是缓解国内农业用水供需压力的重要途径[7]。为进一步精确制定作物灌溉制度，获得作物需水量数据十分关键。潜在蒸散量(ET0)是估算作物需水量的重要参数之一，其与作物系数的乘积即为作物需水量，且该方法已被证明精度较高[8-9]。FAO-56分册规定的Penman-Monteith模型为计算的标准模型，但该模型考虑因素较多，计算过程复杂，限制了该模型的应用[10-11]。因此，在合适的区域找寻合适的ET0简化计算方法，对当地灌溉决策的制定有着十分重要的意义。

目前，针对ET0简化计算方法的研究主要集中在经验模型和机器学习模型两大类[12-13]。其中机器学习模型由于其模型操作方便，且精度较高，被广泛应用于ET0模拟中。毛亚萍和房世峰[14]在新疆区域基于SVM、RF、GBDT和ELM 4种机器学习模型构建了当地ET0预测模型，指出SVM和GBDT这两种算法在日尺度和月尺度都有较好的适用性；张薇等[15]基于ELM模型和GRNN模型两种机器学习模型计算了河北省不同站点的ET0，并与H-S模型计算精度进行了对比，指出机器学习模型精度显著高于经验模型；黄滟淳等[16]基于不同机器学习模型在川中丘陵区构建了ET0预测模型，M5回归树模型计算精度最高。

单一的机器学习模型精度极易受到模型本身结构的影响，造成极值及局部最优解问题，限制模型精度[17]。为避免这一问题的出现，本文基于思维计划算法优化极限学习机模型(MEA-ELM)，以重庆地区为研究区域，分别计算3种不同激活函数下的区域ET0数据，构建重庆地区ET0最优估算模型。

2 研究区域概况及研究方法

2.1 研究区域概况

重庆(E105°17′-E110°11′，N28°10′-N32°13′)是我国重要的直辖市之一，其地处长江上游，物产丰富，是我国重要的农业生产基地。本文选择丰都、奉节、沙坪坝、万州、酉阳共5个站点1980-2016年的逐日气象数据及计算区域ET0。本文数据均来自国家气象中心，气象数据控制良好。

2.2 研究方法

2.2.1ET0计算标准模型

FAO-56分册规定的Penman-Monteith模型为计算ET0的标准模型，该模型由辐射项和空气动力学项两部分组成，具体公式形式可见文献[10,18]。

2.2.2 极限学习机模型(ELM)

极限学习机模型(ELM)主要由输入层、隐含层和输出层3部分组成，设隐含层神经元的激活函数为g(ω，X，b)，则ELM模型输出层表达式为：

(1)

式中：βj为隐含层到输出层的连接值；ωij为输入层到隐含层的连接值；Xi为输入层变量值；bj为第j个隐含层的阈值。

ELM模型激活函数可分为3种：Sine 函数(ELMS)、Radbas函数(ELMR)和Hardlim(ELMH)函数，3种函数具体公式如下：

Sine函数：

g(ωij,Xi,bj)=g(ωijXi+bj)=sin(ωijXi+bj)

Radbas函数：

Hardlim函数：

2.2.3 思维进化算法优化ELM模型构建(MEA-ELM)

MEA算法主要包括7个步骤：网络初始化、隐含层输出计算、输入层输出计算、误差计算、权值更新、阈值更新和判断迭代结果。利用MEA 算法对ELM初始权值和阈值进行优化，可减少ELM迭代次数，利用输入、输出节点数之和与隐含层节点数的乘积，形成每个样本个体的得分函数，基于MEA算法进行迭代，找出最优个体得分，最终得出ELM模型预测结果。具体步骤可见文献[17]。

2.2.4 模型训练与验证

将形成的MEA-ELM算法对应不同的ELM激活函数，形成3种MEA-ELM算法，分别为MEA-ELMsin算法、MEA-ELMRad算法和MEA-ELMHard算法。基于站点1980-2016年的气象资料，以最高温度(Tmax)、最低温度(Tmin)、日照时数(Tsun)、风速(U2)和相对湿度(RH)的不同组合为输入参数，形成不同计算模型，具体形式可见表1。

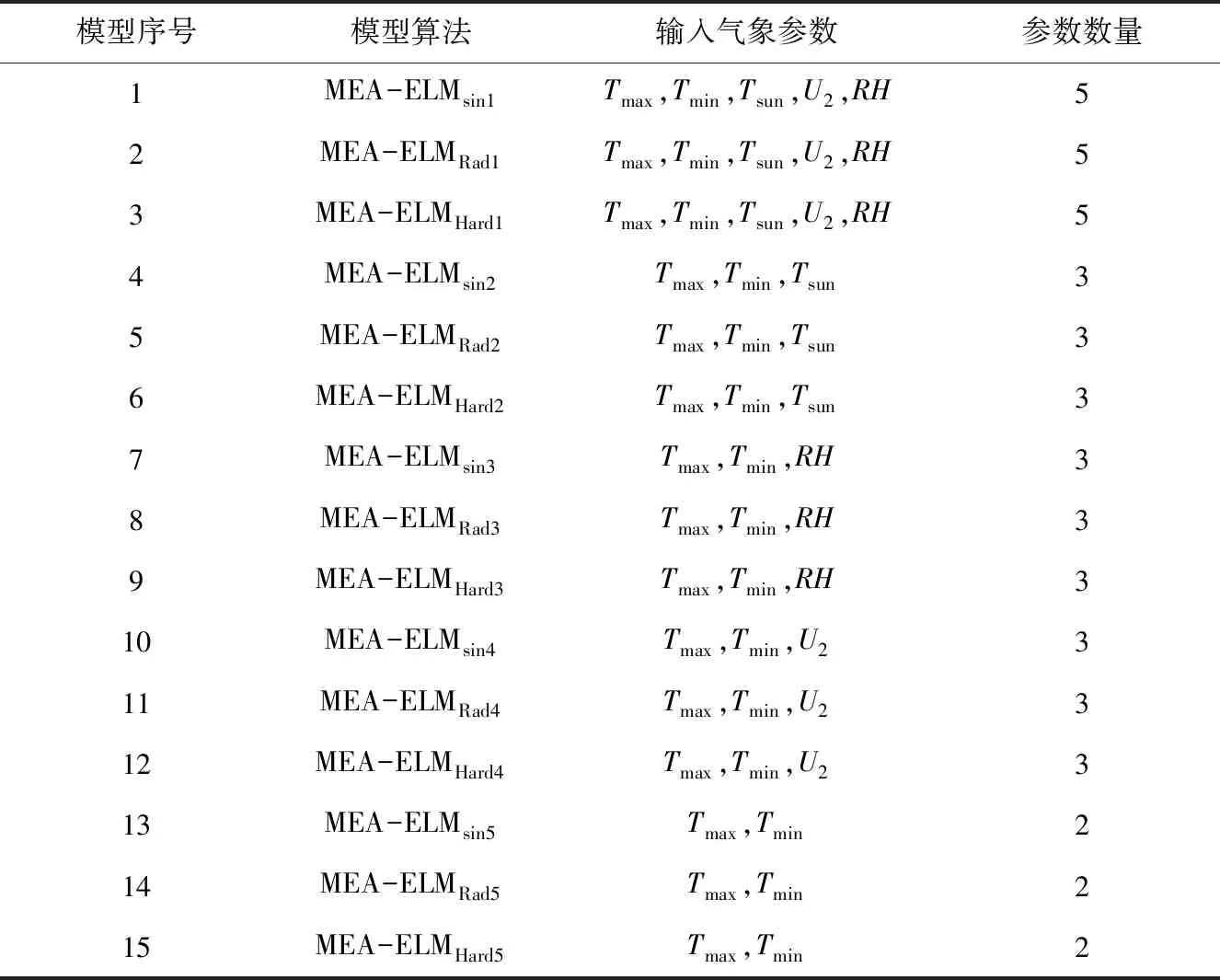
表1 模型参数输入表

2.2.5 模型精度指标构建

分别以均方根误差(RMSE)、平均相对误差(MRE)、纳什系数(NSE)和决定系数(R2)为模型误差评价体系[19-21]，具体公式如下：

(2)

(3)

(4)

(5)

由于评估指标过多，单个评估指标很难比较不同的模型。因此，引入GPI指数来全面评估模型仿真结果，公式如下：

(6)

式中：αj为常数，MRE和RMSE取1，NSE和R2取-1；gj为不同指标的缩放值的中位数；yij为不同指标的尺度值。

3 结果与分析

3.1 ET0年际变化趋势分析

图1为重庆地区不同站点1980-2016年ET0年际变化趋势分析。由图1中可以看出，不同站点多年ET0呈现增长趋势。其中，酉阳站点变化幅度最高，不同站点ET0在1980-2003年呈下降趋势；在2003-2016年呈升高趋势，由于该时段ET0上升幅度较大，导致ET0多年平均呈现上升趋势。丰都、奉节、沙坪坝、万州、酉阳5个站点ET0多年平均变化倾向率分别为0.120、0.123、0.067、0.089和0.236(mm·d-1)/10a。

图1 ET0年际变化趋势及累积距平分析

3.2 ET0年内变化趋势分析

图2为重庆地区不同站点ET0年内变化趋势分析。由图2可以看出，不同站点ET0年内变化趋势均呈开口向下的二次抛物线型式。春冬两季ET0数值相对较小，主要集中在3-10月份的主要作物生长期，1-7月份，各站ET0基本呈线性增长的趋势，在8-12月份呈显著降低趋势；各站点累积距平曲线变化趋势基本一致，呈“减少-增加-减少”趋势，3 个时段分别为 1-3月份、3-9月份和9-12月份。

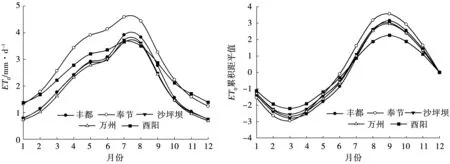
图2 ET0年内变化趋势及累积距平分析

3.3 ET0空间变化趋势分析

图3为不同站点不同时期ET0空间变化趋势。由图3中可以看出，不同时期ET0空间分布趋势基本一致，均呈现由西向东逐渐升高的趋势。在春季，奉节站点附近数值最高，酉阳站点附近次之，其值分别为3.31和2.73 mm/d；夏季变化趋势基本一致，在奉节站点附近最高，达到4.39 mm/d；在秋冬两季，ET0分别在奉节站点和酉阳站点达到最高值。全年和主要作物生长期变化趋势基本一致，均表现为奉节站点附近最高，酉阳站附近次之。

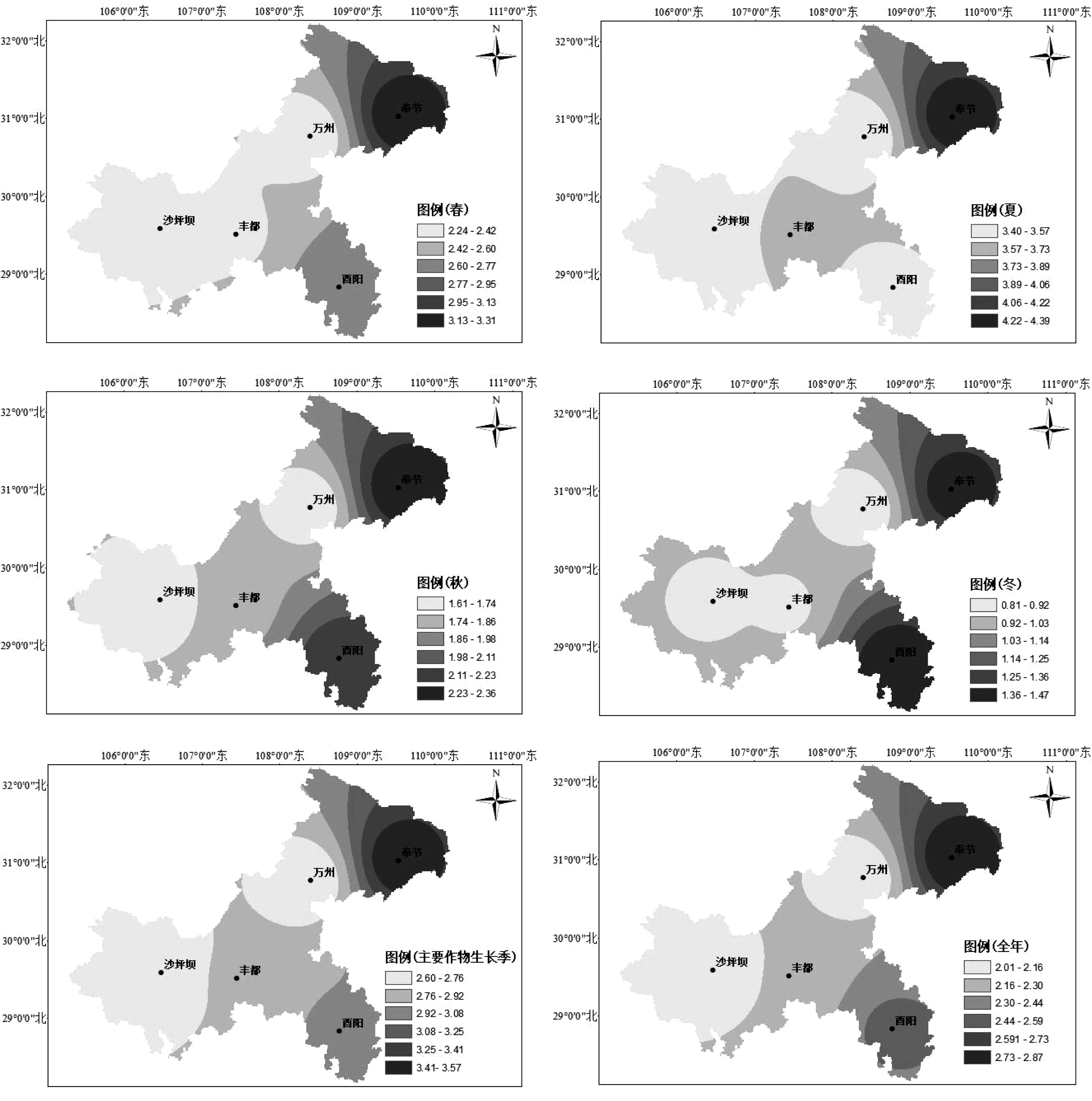
图3 ET0不同时间段空间变化趋势分析

3.4 不同模型ET0精度对比

图4为不同模型ET0模拟精度。由图4可以看出，不同模型输入不同参数时的精度有所差异。输入气象参数组合1时的模型精度普遍最高，其中sin激活函数下的模型精度最高，不同精度指标NSE为0.999、RMSE为0.035 mm/d、MRE为1.13%、R2为0.999，MEA-ELMRad1精度次之，MEA-ELMHard1精度最低；输入参数组合2时，各模型精度有所降低，其中MEA-ELMsin2模型仍保持着较高的精度，不同精度指标分别为NSE为0.990、RMSE为0.14 mm/d、MRE为3.0%、R2为0.990，其余2种模型精度较差；输入参数组合3的模型精度要高于输入参数组合4时的模型，而仅输入温度资料的组合5下的3种模型精度最低。这表明，日照时数的输入可大幅度提高模型预测精度，其对ET0变化的影响程度高于风速和相对湿度。

通过计算不同站点不同模型ET0精度指标的GPI指数，可综合比较不同模型精度，结果见图5。

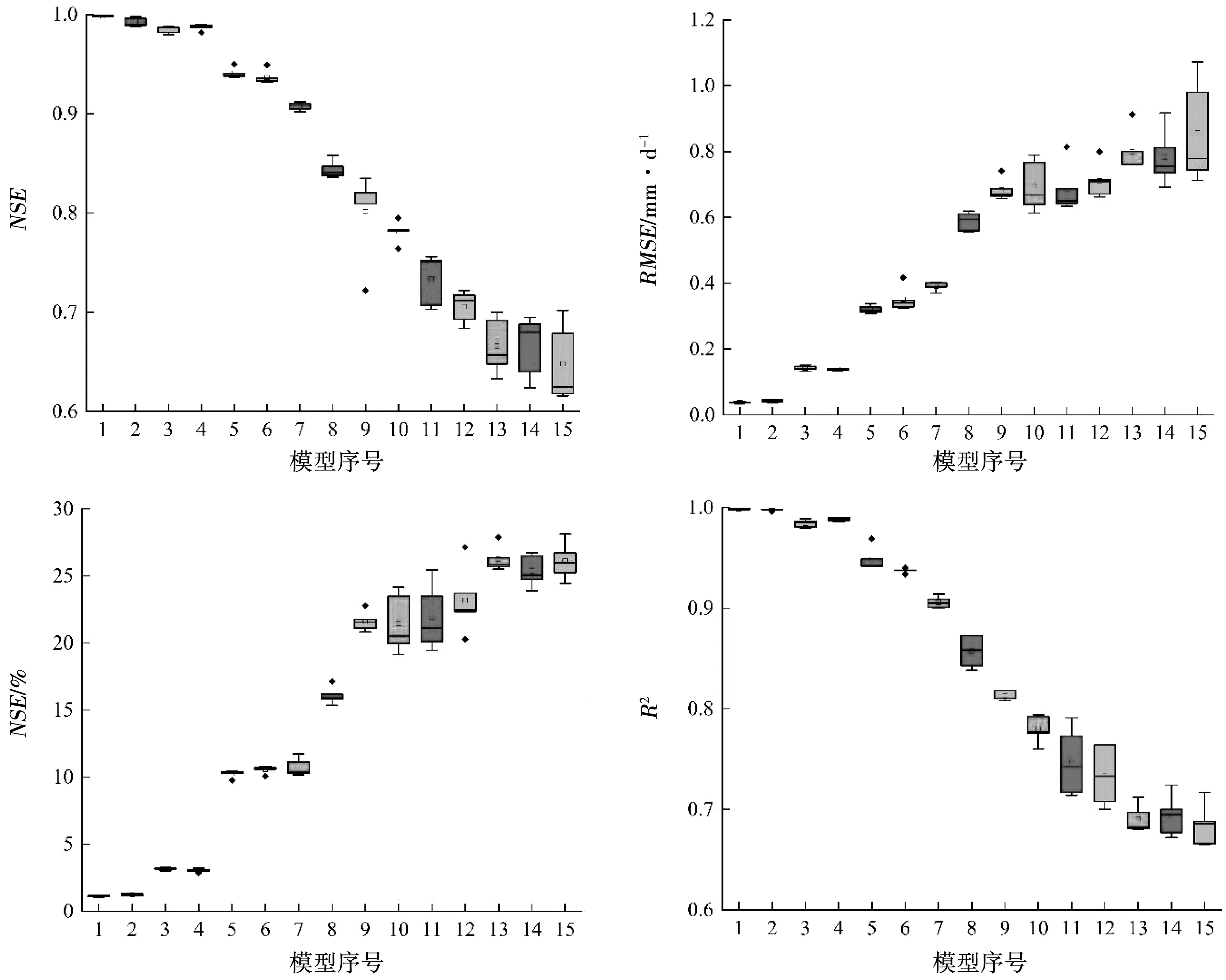
图4 不同模型ET0模拟精度对比

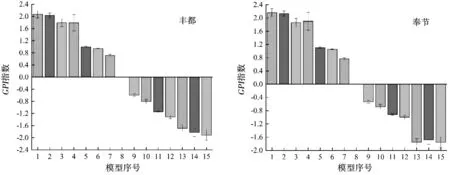
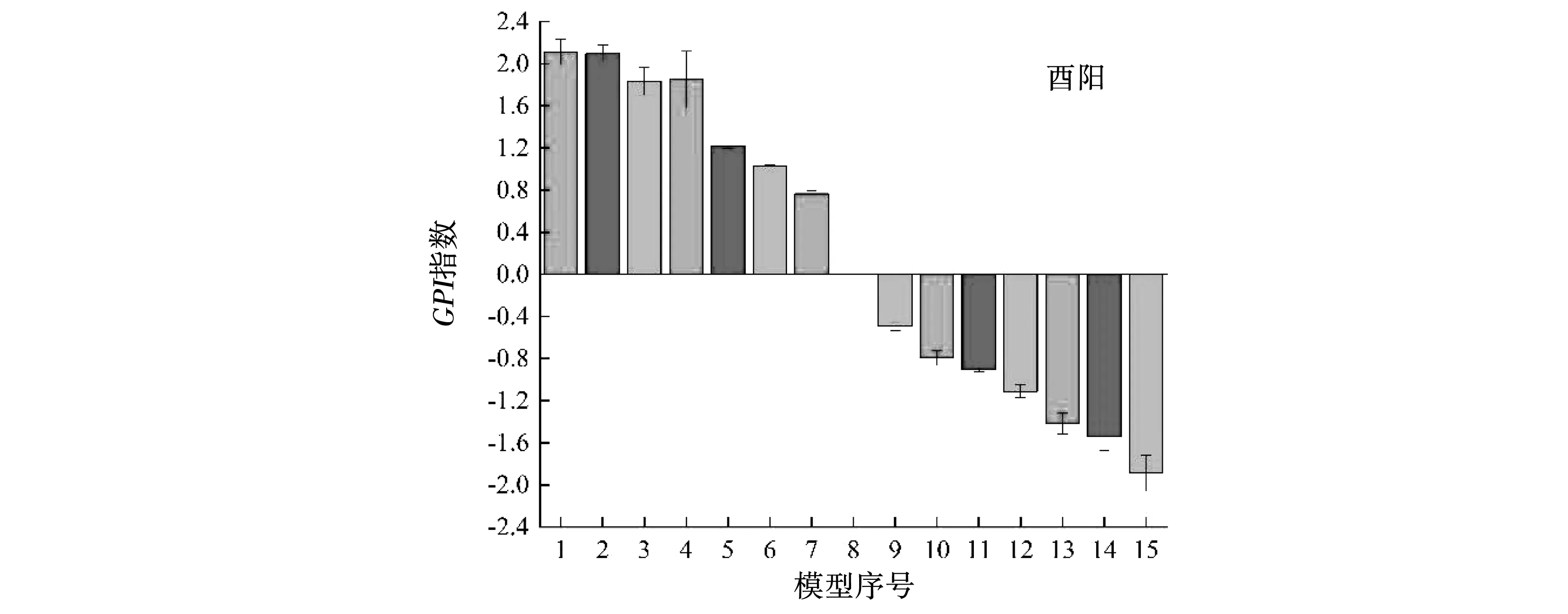
图5 不同站点不同模型GPI指数对比

由图5中可以看出，在不同站点不同模型的模拟精度基本一致，相同输入组合下，3种激活函数对应的MEA-ELM模型精度表现为sin函数>Radbas函数>Hardlim函数；而在相同激活函数下，不同输入组合的模型精度表现为组合1>组合2>组合3>组合4>组合5，这表明当气象数据有限时，已知温度和日照时数数据，即可基于MEA-ELM模型精确模拟ET0。

3.5 不同模型ET0精度对比

为进一步验证精度，本文计算了该模型的可移植性。随机选择其中1个站点的数据作为模拟站点，其余4个站点自动作为训练站点，最终形成20组训练数据，并计算了20组训练数据的精度指标，结果见表2。由表2可知，不同训练组合下的MEA-ELMsin2模型精度较高，其NSE和R2均在0.90以上，而RMSE均在0.35 mm/d以下，MRE均低于11%，这进一步验证了该模型的精度，MEA-ELMsin2模型可作为重庆地区ET0计算的简化标准模型使用。