考虑声固耦合效应的输流管道声振特性分析
2021-06-08陈德锦严谨罗杨阳黄超邹律龙
陈德锦,严谨,罗杨阳,黄超,邹律龙
1 广东海洋大学 机械与动力工程学院,广东 湛江 524088
2 广东海洋大学 海洋工程学院,广东 湛江 524088
0 引 言
输流管道已成为军工、海洋工程和机械等领域不可或缺的一部分,当机械运作或者流体流过管道时,会引起管道振动并在管道内发生声波传递而产生噪声[1]。对潜艇而言,管道振动噪声将直接影响其隐蔽性;对船舶而言,管道振动噪声会对船员的海上生活造成干扰并对航行安全产生威胁。声波检测是管道故障检测的主要手段之一,因此,有必要准确掌握管道振动特性,对内部声波传导特征模态进行研究。
输流管道声振问题多年来一直是声振领域研究的热点之一。输流管道的振动是一种典型的耦合振动,管内流体振荡会引起管道产生机械振动,而管道的机械振动反过来又会影响管内流体的动态行为,这是一种复杂的现象,被称为“典型的动力学问题”[2]。声振问题则是该问题的一种衍生,侧重于由振动所引起的声波传递。因此,研究输流管道的声振不能仅考虑单向耦合,还需考虑管流的双向耦合。研究输流管道双向耦合所用到的理论基础有声固耦合和流固耦合。其中,流固耦合系统计算繁琐、不易收敛,且计算时间较长;声固耦合简化了管道流固耦合系统中的附加质量、附加阻尼和流固耦合项,其运用波传播方法求解输流管道的声振特性,计算效率高,并能针对管道声学特性实现有针对性的解释与分析。目前,考虑声固耦合效应研究管道声振特性的方法主要有数值分析法、解析计算法和实验测试法[3]3种,其中数值分析法最为普遍。文立超等[4]基于一种有限元的模式分析法,对于管道导波的模态频散特性进行了求解,其只对管壁进行了网格划分,证明该方法是有效的。杨国栋等[5]提出了一种Galerkin求解特征方程的方法,其针对浸没圆柱壳结构,对声固耦合模型的自振特性进行计算求解并与算例进行了对比,结果验证了该方法的精确性和可行性。Scott[6]对无限长圆柱壳结构受流体载荷的声振问题进行了研究,对考虑声固耦合效应的圆柱壳结构的自由传播模态进行了分析,对其色散关系的复根含义进行了解释并给出了根的数值解。解妙霞等[7]采用数值分析方法对薄壁液压管道的声振响应予以了计算,对因声固耦合效应而导致声波在薄壁液压管道内传播的能量损失机理进行了探讨。周玉志等[8]联合ANSYS与ACTRAN软件模拟分析了液压输送管道的声学特性,得到了管内为水时输流管道的声压强度分布。利用数值分析方法可以有效分析声固耦合效应对管道声振特性的影响,并可通过设置边界条件来满足实际测试时所需要的外部条件。总体来讲,目前对于考虑声固耦合效应的输流管道声振特性方面的研究较少,且更少有涉及声固耦合影响下管道频散特性和模态振型等机理方面的研究。
本文将通过对输流管道进行数值模拟计算,分析比较考虑声固耦合效应的弹性壁管道与不考虑声固耦合效应的硬声场壁管道的波数频散曲线、管壁的壁厚不同时弹性输流管道的波数频散曲线,以及内部流体介质分别为水、空气和原油时弹性壁管道的波数频散曲线,计算特定激励频率条件下弹性壁输流管道的管壁应力情况,然后通过结果分析得出不同管壁特性和管内不同介质时管道的频散特性、管道应力与内部绝对声压的分布情况,以及管道中弹性波的动态特性。频散曲线可有效区分每个弹性波的特征模态,而分析这些特征模态是管道声波健康检测的主要依据。
1 数值模型的建立
1.1 模型简化假设
声振现象需要满足3个基本方程:运动方程、连续性方程和状态方程。
3D管道模型转化为2D管道模型时,假定如下[9]:
1) 管内为理想流体,声波在管内传播不损耗并且不具有黏滞性;
2) 声波在传播过程中未发生熵变;
3) 管道轻微振动,声学参量忽略二阶及以上的微量;
4) 忽略管内流体流动导致的噪声;
5) 没有声扰动时,管道是均匀、静止的;
6) 声场情况只考虑垂直管道中轴线的截面内。
1.2 计算模型
以二维平面构建无限长管道模型,内部横截面呈圆形。模型直径60 mm,添加的管壁材料为AISI 4 340合金结构钢。管内声学域采用自由三角形划分网格,管壁采用映射划分网格,管道外壁采用自由边界条件。二维管道模型如图1所示,其中模型壁厚为3 mm,管道内壁边界(粗蓝线)即为声固耦合边界。
分别计算管道壁厚为3,4,5 mm情况下的管道波数频散曲线,以及弹性壁(壁厚3 mm)管道内流体分别为空气、水和原油情况下的波数频散曲线,其材料参数如表1所示。

图 1 二维管道模型图Fig.1 Schematic diagram of two-dimensional pipeline model

表 1 材料参数Table 1 Material parameters
2 声固耦合基本理论
2.1 声学控制方程
声波波动方程是从以下3个流体控制方程推演而来[10]。
质量守恒方程:
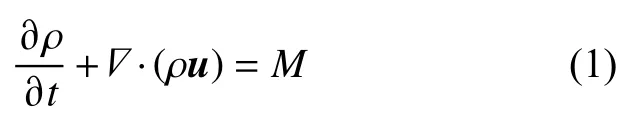
动量守恒方程:

能量守恒方程:

式中:ρ为介质密度;t为时间;p为声学域总压力;u为速度场;s为熵;M和F为可能存在的源项;Δ为哈密尔顿算子。
在经典的压力声学中,假设所有的热力学为等熵过程。在密度为 ρ0(单位:kg/m3)、静态压力为p0( 单位:Pa)的均匀稳定流动流体中,也即u0为常数时,进行小参数展开:

式中,p1,ρ1,u1,s1为微小声学扰动量。因此,压强微小变化量p1远 小于p0, 密度微小变化量 ρ1远小于 ρ0, 速度微小变化量 |u1|远 小于声速c。假设初始熵s0为0,将这些值插入控制方程,只保留声学变量中的线性项,可得


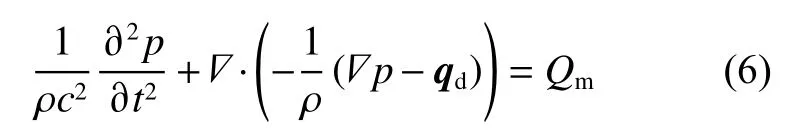
式中:Qm为单极子源,1/s2,该源对应于式(1)中的一个质量源;qd为偶极子源,N/m3,其对应于式(2)中的一个定义域力源。
2.2 结构控制方程
固体的声固耦合控制方程是根据动量守恒方程决定的。当管壁特性为弹性壁时,方程如下:
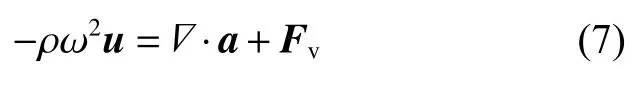
式中:ω为角频率,a为第2类皮奥拉-克希荷夫应力张量,作用是联系空间方向的作用力与原始未变形构型中的区域;Fv为体积力。
当管壁特性为硬声场壁时,方程(7)中等号左边项为0,即

2.3 边界条件
声固耦合边界条件包括作用在结构上的流体载荷和流体所经历的结构加速度[11],其外部边界条件为:
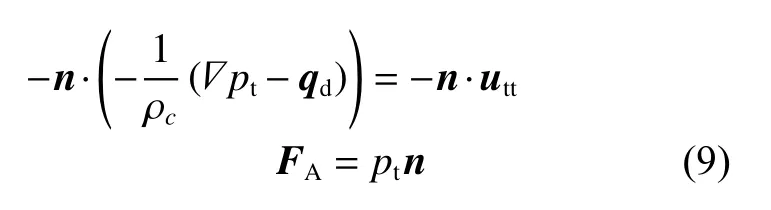
式中:n为 耦合面法向量;utt为 结构加速度; ρc为声学介质的密度;pt为总声压;FA为结构所承受的载荷(单位面积力)。
得到的内部条件为:
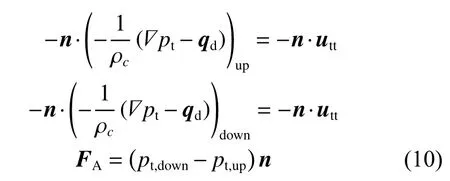
声学载荷由压降决定。式(10)中,下标up,down指内边界的两边。
当管壁特性为硬声场壁时,utt=0,即管壁不受声学域的声压影响而引起法向加速度变化,方程表示为

2.4 截止频率方程
对频域方程使用非齐次亥姆霍兹等式,得

式中,keq为径向波数。在二维场中,

式中:cc为 声学域中声速; ω=2πf,为角频率;κz为轴向波数,在激励频率f已知的情况下,不能传播κz为负的模态。
根据式(13),可以推导出各个模态的截止频率计算公式。推导如下:
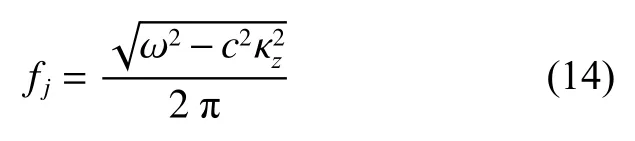
当不存在外载荷时,式(12)可以化简为

将式(15)运用柱坐标系(坐标如图2所示)下的拉普拉斯算符表示为:

式中:r为径向坐标;φ为极角;z为轴向坐标。然后,再利用“分离变数法”解式(16),令p(r,φ,z)=R(r)φ(φ)Z(z),则可求得波管中声场的形式解为
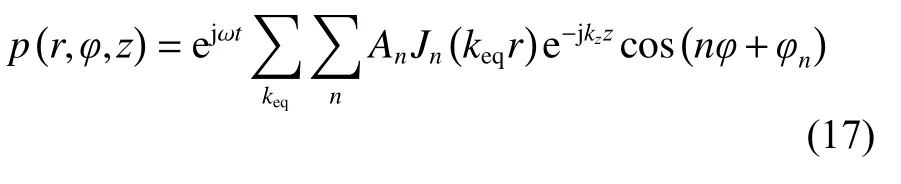
式 中:An为 声 压 幅 值;φn为n阶 声 压 初 相 位;Jn为n阶贝塞尔方程的解。

图 2 管道坐标示意图Fig.2 Pipeline coordinate diagram
3 管道声振模态分析
3.1 管道声压应力分布
为了验证声固耦合效应的影响,本文利用COMSOL Multiphysics多物理场仿真软件中的声学模块与结构力学模块,分析了考虑耦合效应的弹性壁和不考虑耦合效应硬声场壁管道内部声场的区别与联系。
为了验证计算结果的准确性,首先将COMSOL Multiphysics中频域分析模块对管道干、湿模态的计算结果与ANSYS Workbench中Modal和Acoustic模块对管道干、湿模态的计算结果进行比较,流程如图3所示。
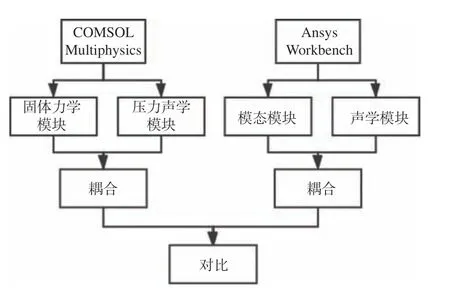
图 3 计算流程示意图Fig.3 Schematic diagram of calculation process
计算得到前4阶的固有频率(单位:Hz)如表2所示。
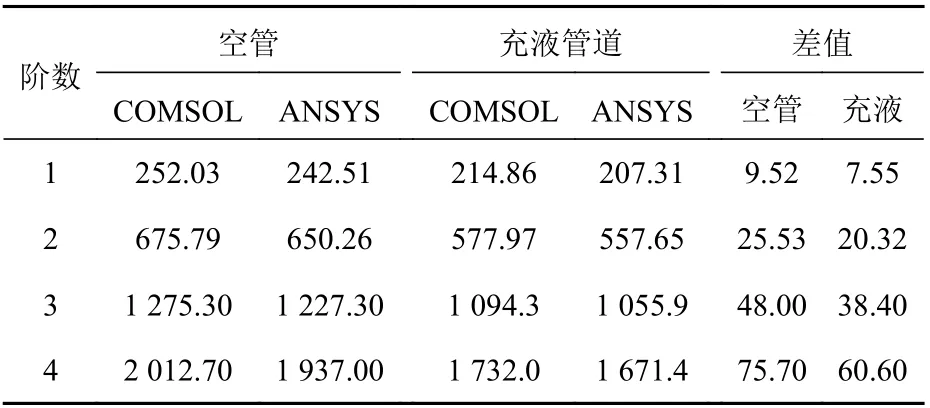
表 2 COMSOL和ANSYS的计算对比Table 2 Comparison of calculations between COMSOL and ANSYS
由表2可以看出,两者计算之间的差值均控制在4%以内,说明两者的计算结果非常接近。其中,充液管道的固有频率与空管相比有所降低,这主要是由内部液体与管道耦合作用所导致,结论与文献[12]中的一致,说明使用COMSOL Multiphysics软件进行声固耦合效应的管道声振特性研究计算结果可靠、准确。
将模式分析中的激励频率f设为10 000 Hz,搜索基 准 值 设为 1.1×k(其 中 波数k=2πf/c0,此 处2πf=ω,c0为水中声速)。采用并行稀疏直接求解器求解特征值,计算绝对声压的应力分布,然后分别取计算所得相同面外波数的连续4阶模式数情况分布图进行合理、有效的对比分析,如图4所示。其中:左、右图分别为弹性壁管道和硬声场壁管道绝对声压应力分布图;每幅图中左、右标尺数值分别表示结构总位移(单位:mm)和绝对声压(单位:Pa)。
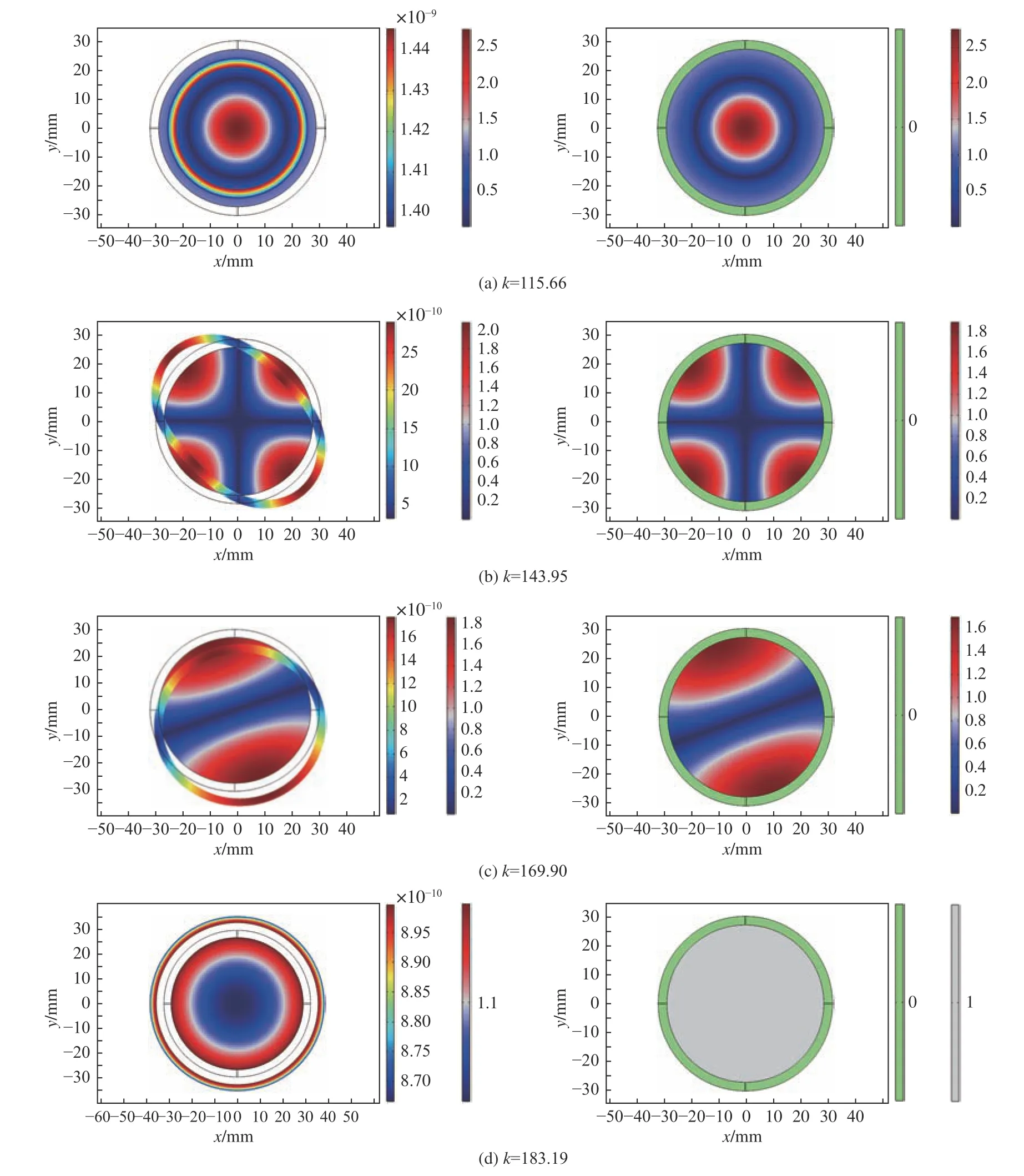
图 4 管道绝对声压应力云图Fig.4 Absolute sound pressure stress contours diagram of pipeline
由图4所示硬声场壁管道绝对声压应力分布图(右图)可知,基于硬声场边界本身的特性,加速度法向方向为0,所以不考虑硬声场管壁的形变情况。由图4所示弹性壁管道绝对声压应力分布图(左图)可知,在给定激励频率f下,弹性壁管道拥有不同阶的振型,每个波数对应一个振型。在绝对声压较高的地方,变形情况较为突出,这些不同位置的变形情况可为管道支撑提供一定的理论依据。从图4可以看出,声波垂直于截面向内传播,随着面外波数的增大,声压沿半径方向逐渐增大。硬声场壁无限长管道内部声压分布与弹性壁无限长管道的情况基本相同,即声固耦合效应对内部为空气的无限长输流管道内部声压分布影响不大。从图4(d)可以看出,当波数k=183.19时,硬声场壁管道没有传播模式,说明没达到此截止频率,无法产生此模态。
3.2 管道频散关系
3.2.1 管壁属性的影响
为精确描述声波在管道中传播的动态特性,需进一步确定硬声场壁与弹性壁无限长输流管道的区别和联系,以及壁厚不同和内部流体不同时管道的频散特性,分析波数与频率的关系。利用参数化进行扫描计算,频率范围为100~12 000 Hz,其中间隔取100 Hz,求解模式数设为6。硬声场壁和弹性壁无限长管道的频散关系曲线如图5所示。
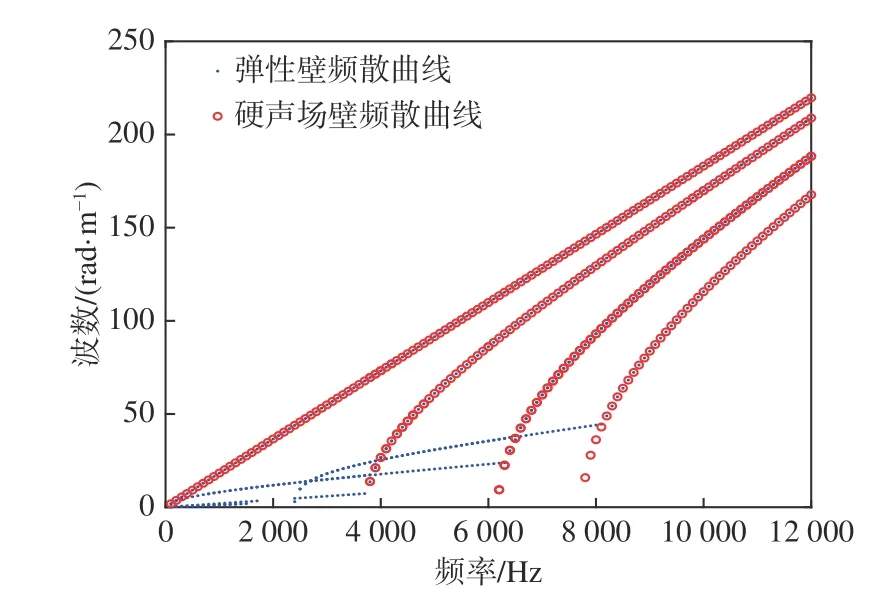
图 5 管道频散关系图Fig.5 Pipeline dispersion relation diagram
由图5可以看出,弹性壁无限长管道第1阶弹性模态的截止频率为2 400 Hz,硬声场壁无限长管道第1阶弹性模态的截止频率为3 800 Hz。硬声场壁管道的传播模态数比弹性壁管道的少,弹性壁管道增加的模态数主要为管道的形变模态,例如径向模态等,说明声固耦合使弹性壁对管道内部声波传播的模态数产生了影响。由于声固耦合效应,弹性壁管道平面波模态的波数有些可能大于硬声场壁,在100 Hz处,根据式(14),计算的硬声场壁管道平面波模态的波数为1.832 rad/m,弹性壁管道对应的波数值为2.478 rad/m;在150 Hz处,计算的硬声场壁管道平面波模态的波数为2.747 rad/m,弹性波管道对应的波数值约为3.039 rad/m。这些计算值求出的硬声场壁模态截止频率是纯虚数,因此,硬声场壁是没有这种模态的。根据以上结论,可以准确得出管道弹性壁与硬声场壁的区别,并通过频散关系图得出他们之间的频散关系。
3.2.2 管壁厚度的影响

图 6 不同管壁厚度下的频散关系图Fig.6 Dispersion relation diagram of different wall thickness
结构是影响管道声振特性的因素,所以需要分析管壁厚度对硬声场壁与弹性壁管道频散关系的影响。本文分别取管壁厚度为3,4,5 mm,内部流体域为空气,不同管壁厚度下的频散关系曲线如图6所示。由图6可以看出,随着管壁厚度的增加,不管是硬声场壁还是弹性壁管道,频散曲线的个数不变,斜率基本没有变化,表示产生的弹性波特征模态形态基本不变;随着管壁厚度的增加,频散曲线均向高频移动,除直通模式外,说明声学模态的截止频率发生了改变,因此管壁较厚的管道需要更大的激励频率才能激发出与管壁较薄的管道同阶模态的导波模式。管壁厚度为3 mm的弹性壁无限长管道第1阶弹性模态的截止频率由上文已知为2 400 Hz,管壁厚度为4,5 mm时分别为3 300和4 200 Hz,即每增加1 mm壁厚,该阶截止频率向右平移900 Hz。
3.2.3 管内流体介质的影响
管内流体域介质也是影响管道声振特性的一个重要因素。本文分别取管内流体为空气、水和原油,内部为不同流体介质下的频散关系曲线如图7所示。由图7可以看出,管道内部介质为空气时的频散曲线与内部介质为原油和水时的频散曲线区别较大,说明内部介质为液体时与为气体时声波传播模式是有较大区别的;内部介质为空气时,硬声场壁中的几个导波模态与弹性壁中的导波模态能够一一对应;内部介质为原油与内部介质为水时的频散曲线较为相似,两者在硬声场壁条件下只存在直通模式,并且弹性壁和硬声场壁的直通模式存在偏差;当内部介质为气体时,在不同的扫描频率段,弹性波波数明显高于液体介质;内部介质为原油和水时其频散关系的区别主要在于直通模式的斜率,原油的斜率要高于水的斜率,说明介质密度对频散曲线有一定的影响。以上性质可以有效运用于管内流体域介质性质的区分。
4 结 语
本文考虑声固耦合效应,通过数值计算,对二维硬声场壁管道和弹性壁管道的声振特性进行了研究。首先,分析管道的干、湿模态并验证了声固耦合模型的合理性;然后,在特定激励频率情况下,分别计算得出硬声场壁管道和弹性壁管道的内部绝对声压分布图,以及弹性壁管道的管壁变形情况;最后,针对不同壁厚和不同内部介质进行特征模态分析,通过参数化扫描计算其频散关系,绘制了波数-频率频散关系曲线图,分析表明声固耦合会影响管道声波传播的模态数,弹性壁管道的模态数要比硬声场壁管道的多。而且,结果显示了弹性壁和硬声场壁管道内部绝对声压分布情况基本一致;不同壁厚对管道的特征模态形式影响较小,随着壁厚的增加,每阶截止频率也随之增加;管内流体介质为气体和液体时特征模态区别较大,液体之间的区别主要体现在直通模式上。

图 7 内部为不同流体介质时的频散关系图Fig.7 Dispersion relation diagram of different internal fluids
