基于多层复杂网络的轨道交通产业链优化

薛 锋，范千里，罗 建

基于多层复杂网络的轨道交通产业链优化

薛 锋1, 2，范千里1，罗 建3

（1. 西南交通大学，交通运输与物流学院，成都 611756；2. 综合交通大数据应用技术国家工程实验室，成都 611756；3. 西华大学，汽车与交通学院，成都 610039）

为对轨道交通产业链进行网络性能优化，首先，基于复杂网络理论，采用SpaceL法建立了轨道交通产业链依存性多层复杂网络拓扑结构，描述轨道交通产业链基本结构；随后，选取相关评价指标，运用蓄意攻击、随机攻击的方式，分析了轨道交通产业网络性能在攻击下所表现出的变化趋势及相关特性，并结合熵权法以及节点收缩方法，分别对节点与边的相对重要性、关键节点的位置以及加大投入下关键节点的重要度变化趋势进行分析；最后，以成都轨道交通产业链为例进行了分析验证。结果表明：轨道交通产业链多层复杂网络在受到攻击时点相对于边有更高的重要度，对网络中的节点加大投入时，网络中某些节点，特别是关键节点，对短期内快速优化网络性能有着显著的作用。

交通运输经济；网络性能；多层复杂网络；轨道交通产业链；双层网络模型

0 引 言

随着轨道交通产业的不断升级与发展，产业链逐渐变为一个复杂的网络结构，企业之间相互作用、相互制约，呈现一定的复杂性。提高轨道交通产业链整体的网络性能，对轨道交通产业链中各项生产要素和功能环节进行合理配置，成为当前轨道交通产业亟须解决的问题。

产业链本身就是一个复杂的网络结构，将复杂网络理论应用到产业链的研究中，对于丰富和深化产业链理论，提高轨道交通产业链的稳定性有重要意义。目前，国内在应用复杂网络解决交通运输领域问题方面已有较多研究成果。毕京浩等[1]运用多层复杂网络理论建立了空铁结合的交通多层复杂网络模型，并分析了其脆弱性；高鹏等[2]提出了一种基于复杂网络的变权重城市轨道交通网络鲁棒性分析方法；叶青[3]运用复杂网络对轨道交通网络的脆弱性进行分析；张欣[4]对多层复杂网络近期发展历程和代表性研究进行了回顾和梳理，从概念、理论模型和数据三方面入手，阐述了多层复杂网络的科学本质、理论瓶颈及现实应用。国外关于复杂网络的研究也较为成熟，Vito[5]以波士顿地铁网络为例，通过识别和保护其中的关键站点来减轻蓄意攻击的影响；Taylor[6]等将复杂网络的脆弱性分为两个部分：节点脆弱性和路段脆弱性。在产业链的研究方面，黄倩[7]等运用复杂网络理论和改进的PageRank算法，定量分析轨道交通产业集群网络的拓扑指标，探讨其发展现状和方向；刘斐[8]在分析产业链内涵和轨道交通产业的基础上，提出了轨道交通产业链的内涵，构建了轨道交通产业链双链模型；戴眉眉[9]提出了基于复杂网络的产业链风险传播模型；方伯芃[10]等对产业链生产与配送协同调度优化问题进行了研究，通过启发式寻优求解出不确定环境下产业链生产与配送协同调度问题的最优方案；员学锋[11]等通过物质流和能量流分析产业链运行状况和存在问题，优化资源配置方案，促进农业园区生态保护和资源环境的永续利用。

在既有文献中，将复杂网络理论和产业链理论相结合的研究较少，大部分集中于运输网络与复杂网络相结合。虽然运输网络与轨道交通产业链网络的建模以及攻击所代表的性质完全不同，但其建模、攻击以及测算重要度的方法具有一定的相似性，现有的文献具有一定的参考意义。本文运用多层复杂网络理论建立轨道交通产业链复杂网络模型，并以成都市轨道交通产业链为例，分析网络中各个要素对整体网络性能的重要程度，以期为成都市轨道交通产业链的优化及合理配置提供决策支持。

1 轨道交通产业链双层网络构成

在建立复杂网络的过程中，常用的建模方法有4种，分别为SpaceL法、SpaceP法、SpaceB法、SpaceC法。其中，SpaceL法将轨道交通产业链中的企业作为节点，如果任意两个企业之间有人员、资金、业务上的往来，则可以认为他们之间有边直接相连。SpaceL法是轨道交通产业链最为直观的表现形式，同其他建模方法相比，主要用于研究系统的拓扑结构特性和脆弱性，对于本文中轨道交通产业链网络性能以及关键节点的研究有较为有效的支撑作用。由于轨道交通产业链是一个双链模型，即轨道交通工程建设产业链和轨道交通产品产业链[8]，若只采用单层复杂网络构建，则无法较好地反映两条链中各个节点的相互关系。因此，采用多层复杂网络理论，针对两条子链分别构建复杂网络，由于部分节点分别位于两层网络中，将这些节点相连，从而获得一个双层网络。

在轨道交通产业链的多层网络中，节点是指网络中各个具体单位，边是指产业链多层网络中的单位之间存在着一定的关联度。由于网络中任意两单位之间的关联是双向且相互影响的，因此本文构建的轨道交通产业链双层网络是一个无向网络。

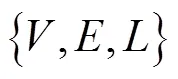
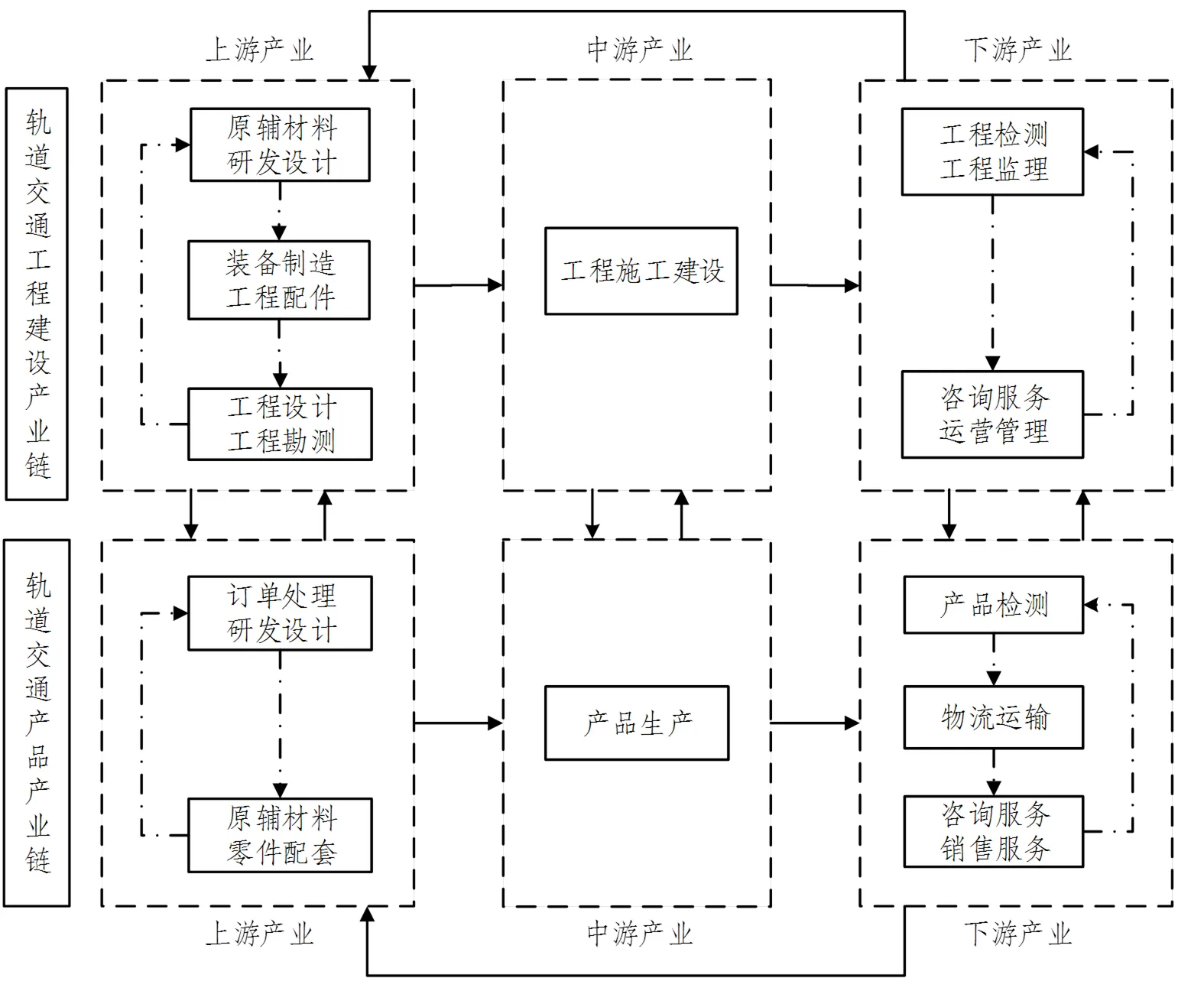
图1 轨道交通产业链结构示意图

2 轨道交通产业链多层网络性能分析

2.1 点和边对网络性能的相对重要度分析

2.1.1 攻击策略

通过对轨道交通产业链双层网络分别进行蓄意攻击、随机攻击，并分析网络在被攻击后稳定性评价指标的变化趋势，可以分辨出在多层网络中边和点的相对重要性。在攻击下，每移除一个节点（边）后重新计算网络中各项评价指标。算法的具体步骤如下：

Step1 读取现有的轨道交通产业链网络，网络以邻接矩阵的形式储存；

Step3 运用相应的攻击策略对点（边）进行攻击；

Step4 判断网络中的节点（边）是否为0，若不是0，则更新邻接矩阵，转到Step2进行计算，否则循环结束；

Step5 输出结果。

2.1.2 攻击对象选取

采取随机攻击与蓄意攻击的方式对轨道交通产业链双层网络进行攻击，其中，进行蓄意攻击与随机攻击的节点或边的选取方式如下：

（1）蓄意攻击

② 边介数定义为网络中所有最短路径中经过该边路径的数目占最短路径总数的比例，因此，边介数越大，其边的重要性就越高。因此，对边的蓄意攻击对象可优先选取在目前网络中介数最大的边进行攻击。

（2）随机攻击

在随机攻击中，对节点或边攻击对象的选取采用完全随机的方式，随机选择某一个节点或某一条边进行攻击。

2.1.3 网络指标的选取

为测定轨道交通产业链网络的网络性能，需要选取相应的评价指标定量分析网络中节点和边，从各个角度很好地评估网络整体性能。本文选用的网络性能指标定义如下：

（1）平均路径长度

对于轨道交通产业链网络而言，当平均路径长度较小时，从网络中的一个节点到达其他节点的最短路径越小，网络中节点单位之间沟通难易程度相对而言比较容易，轨道交通产业链网络性能越高。平均路径长度的计算公式如下：

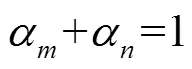
（2）网络凝聚程度

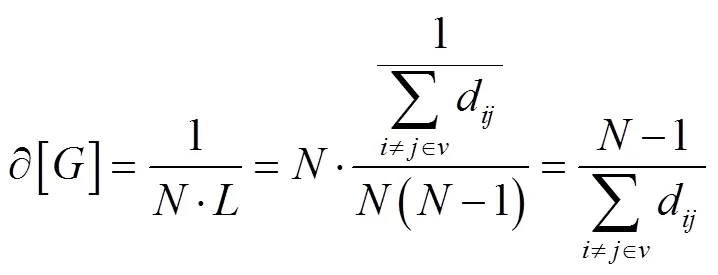
（3）可达节点对比例

网络中两个节点之间有一条或几条路径相连接，即它们之间存在通路，称这两个节点间是可达的。在轨道交通产业链网络中，存在通路相连的节点对数与网络中总节点对数之比称为轨道交通产业链网络的可达节点对比例。可达节点对比例的计算方法如下：

2.1.4 各指标权重确定

由于各项指标对于网络的影响度大小不同，故需要对指标进行合理的指标权重分配，熵权法是一种应用最为广泛的客观确定权重的方法，因此本文采用熵权法[12]确定各项指标的权重，具体步骤为：

（1）数据标准化

（2）求各指标的信息熵

根据信息论中信息熵的定义，一组数据的信息熵为：

（3）确定指标权重

通过信息熵计算各指标的权重：

计算出指标权重后，总体的指标可以定义为：

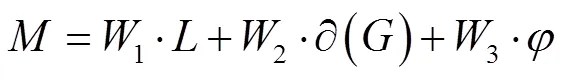
2.2 单个节点对网络性能的重要度分析

基于文献[13]中提出的节点收缩方法，运用网络凝聚度这一指标，给出基于网络凝聚度的节点重要度评估方法。重要度计算方式如下：

利用公式（9）对轨道交通产业链双层网络中的节点重要度进行评估，能够得出关键节点。算法的具体步骤如下所示：

在得到关键节点后，分析其在加大投入条件下，关键节点重要度的变化趋势，更好地判断节点重要度。在本文中，对网络某节点加大投入可处理为缩短该点到达其他节点的距离，每次加大投入，可假设该节点与其他相邻节点间的距离缩短了10%。

3 实例分析

成都轨道交通产业发展速度和规模在全国处于前列，本文以成都市轨道交通产业链为例进行分析，并对产业链进行合理配置。

3.1 成都市轨道交通产业链双层网络模型的建立

成都在轨道交通方面的资源十分丰富，初步形成了较为完善的产业体系。将成都轨道交通产业链的主体企业分为轨道交通工程建设产业链相关企业和轨道交通产品产业链相关企业，如表1、表2所示。

表1 成都轨道交通工程建设产业链相关单位

续表1

序号单位名称归属产业链 1-13中铁二十三局中游产业 1-14四川铁建中游产业 1-15成都铁路局下游产业 1-16成都地铁公司下游产业

表2 成都市轨道交通产品产业链相关单位

本文采用matlab2018A建立轨道交通产业链多层复杂网络模型，并结合前文所述的方法，对成都市轨道交通产业链网络进行重要度评价。根据成都轨道交通产业链双层网络的相关信息，对其进行建模后，可以得到成都轨道交通产业链双层网络模型如图2所示。

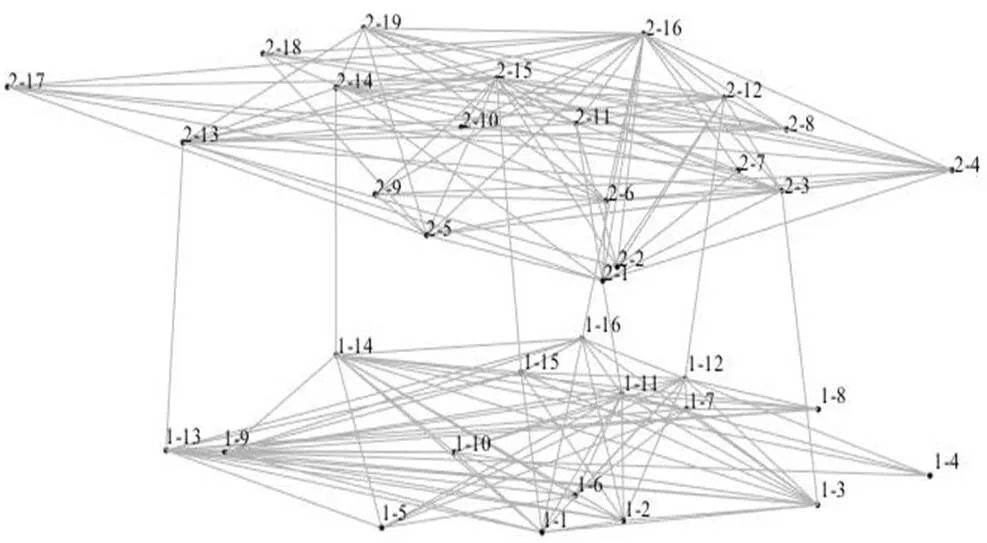
图2 成都轨道交通产业链网络拓扑图

现对根据上述方法建立的成都市轨道交通产业链网络进行基本概念的界定：

（1）度值

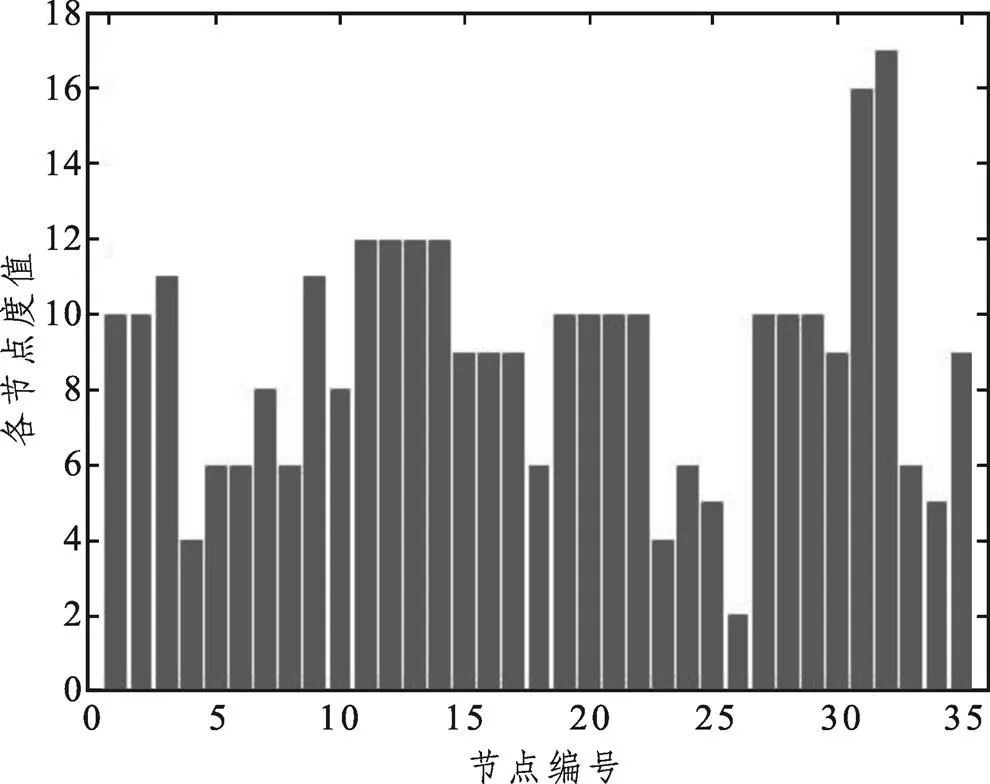
图3 成都市轨道交通产业链网络各节点度值

由度值分布图可知，大部分节点企业都有较高的度值水平，且度值多分布在6和10之间。

（2）平均路径长度

经统计计算，成都市轨道交通产业链网络平均路径长度=2.884，这说明成都市轨道交通产业链网络中平均最短路径较小，网络中大部分节点的最短路径长度并不大，节点企业之间的沟通难易程度较小，平均经过2个节点就能到达目标节点企业。同时也说明轨道交通产业链网络具有“小世界”网络特点。

（3）聚类系数

成都市轨道交通产业链网络的聚类系数反映了成都市轨道交通产业链中节点的聚集程度。当聚类系数较大时，说明网络中节点企业附近联系较为密切，在这种情况下网络中某个节点企业由于某种原因无法发挥作用时，对整个网络的连通性不会造成较大影响，网络整体的容错性较高；当聚类系数较低时则说明网络结构较为脆弱，网络稳定性不高。

经过计算可得整个网络的平均聚类系数为0.179 6，这表明轨道交通产业链节点企业的聚集程度并不高，节点企业的相互联系不紧密。网络中一部分节点的聚类系数为0，说明成都市轨道交通产业链网络中部分相邻的三个节点企业不存在直接连通的线路使它们形成环路。容错性能较差，当网络中某个关键性节点企业遭到破坏时，很容易造成网络的不连通。

3.2 基于节点和边失效的轨道交通产业链稳定性分析

在轨道交通产业链网络中，节点或边的失效会对网络拓扑结构的连通性造成破坏，从而导致网络性能的下降。分别运用蓄意攻击和随机攻击[1]的方式攻击节点和边，分析性能的变化趋势。

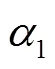
图4 基于边失效稳定性指标的变化趋势

以往的研究表明，在异质性单层复杂网络中，度大的节点或介数大的边对于维护网络的稳定性有着更加重要的作用，若随机将一部分节点从网络中删除，网络表现出非常强的稳定性，而当有目的性地删除节点或边时，网络则特别脆弱[14]。从图4与图5可以发现，轨道交通产业链双层复杂网络同样表现出了这样的特性，但网络崩溃所需失效的节点或边的比例差别不大，特别是基于边失效的网络稳定性，随机攻击和蓄意攻击所需失效的边比例基本相同。但在蓄意攻击下仅失效了部分节点或边网络性能就急剧下降，而随机攻击下需要大部分节点或边的失效才会导致网络性能的下降。

在分析图6与图7可以发现，在蓄意攻击中，开始节点和边的失效导致网络性能的下降趋势基本相同，而随着节点和边失效比例的逐步增加，节点失效所导致的网络性能的下降趋势急剧增加。但在随机攻击中，两者的下降趋势却基本相同，节点失效所导致的网络性能下降趋势略微大于边失效所导致的网络性能下降趋势。这说明从整体的角度看来，面对蓄意攻击，节点失效对于整个双层网络造成的伤害比边失效大得多，而面对随机攻击，节点失效对于整个双层网络造成的伤害略微大于边失效。

图6 蓄意攻击中基于节点和边失效的网络性能指标变化趋势

图7 随机攻击中基于节点和边失效的网络性能指标变化趋势

3.3 单个节点对轨道交通产业链网络性能的影响

运用节点收缩的方法，对成都市轨道交通产业链多层网络进行节点重要度评估，得到各个节点的重要度程度，如表3所示。

表3 单个节点对轨道交通产业链网络的影响重要度

根据表3可知，在轨道交通产业链多层网络中，对维持整个网络的网络性能而言最重要的两个单位是中国铁路成都局集团有限公司和成都轨道交通有限公司，由于轨道交通产业的需求基本来源这两个公司，分析所得结果与实际情况基本符合；其次，西南交通大学、中铁二局、中铁八局、中铁二十三局与四川铁建所求得的重要度程度仅次于中国铁路成都局集团有限公司和成都轨道交通有限公司。为更准确反映出节点对网络性能的影响程度，对以上节点加大投入，观察其节点重要度变化趋势。

由图8可以看出，虽然当前网络中中国铁路成都局集团有限公司和成都轨道交通有限公司重要度最高，但随着投入的逐渐加大，中国铁路成都局集团有限公司和成都轨道交通有限公司的重要度提升较小。而相反，四川铁建、西南交通大学、中铁二局等单位重要度上升较快，最后所有关键节点重要度都大致达到1是由于随着投入逐步增加，都变为重要度为1的关键节点。

图8 加大投入后关键节点重要度变化趋势

根据以上分析，关键节点为中国铁路成都局集团有限公司、成都轨道交通有限公司、西南交大、中铁二局、中铁八局、中铁二十三局与四川铁建，若想在短期内加强成都市轨道交通产业链的网络性能，可以对四川铁建、西南交通大学、中铁二局等单位加大投入。

4 结束语

（1）轨道交通产业链双层复杂网络在蓄意攻击中，网络性能急剧下降，相反的，在随机攻击下，最初不会出现网络性能的急剧下降，直到大面积节点或边被删除后，才出现网络性能的急剧下降。

（2）在整个成都市轨道交通产业链中，面对蓄意攻击，相比于边的重要度程度，节点的重要度更高，整个网络性能的发挥更依赖于节点，而面对随机攻击，节点重要性略高于边。因此，总体而言，加强对节点企业的建设可以对产业链进行优化。而对于整个网络中节点而言，中国铁路成都局集团有限公司、成都轨道交通有限公司、西南交大、中铁二局、中铁八局、中铁二十三局与四川铁建的重要度程度较高，这与成都市轨道交通产业链的实际情况相符合。

（3）在加大投入的条件下，中国铁路成都局集团有限公司、成都轨道交通有限公司重要度的增长较为缓慢，相比之下，西南交大、中铁二局、中铁八局、中铁二十三局与四川铁建的增长更为快速，在短期内能见成效。

[1] 毕京浩. 基于多层复杂网络理论的交通网络脆弱性研究[D]. 济南: 济南大学, 2016.

[2] 高鹏, 胡剑波, 魏高乐. 变权重的城市轨道交通复杂网络鲁棒性分析[J]. 计算机仿真, 2013, 30 (9): 153-156.

[3] 叶青. 基于复杂网络理论的轨道交通网络脆弱性分析[J]. 中国安全科学学报, 2012, 22 (2): 122-126.

[4] 张欣. 多层复杂网络理论研究进展: 概念、理论和数据[J]. 复杂系统与复杂性科学, 2015, 12 (2): 103-107.

[5] VITO L, MAAIMO M. How the science of complex network can help developing strategies against terrorism[J]. Chaos, Solitons and Fractals, 2004, 20 (1): 69-75.

[6] TAYLOR M A P, SEKHAR S V C, D'ESTE G M. Application of accessibility based methods for vulnerability analysis of strategic road networks[J]. Networks & Spatial Economics, 2006, 6 (3): 267-291.黄倩, 薛锋. 基于改进PageRank算法的轨道交通产业集群分析[J]. 交通运输工程与信息学报, 2020, 18 (2): 30-38.

[7] 刘斐. 成都轨道交通产业链构建研究[D]. 成都: 西华大学, 2010.

[8] 戴眉眉. 产业链复杂网络演化模型及风险传播模型研究[D]. 南京: 南京航空航天大学, 2012.

[9] 方伯芃, 孙林夫. 不确定环境下的产业链生产与配送协同调度优化[J]. 计算机集成制造系统, 2018, 24 (1): 224-244.

[10] 员学锋, 姚一晨, 宋成军, 等. 基于物质流和能量流分析的循环农业园产业链优化[J]. 农业工程学报, 2018, 34 (15): 228-237.

[11] 薛锋, 余潇. 基于熵权-灰色理论的高速铁路产业链关联分析—— 以四川省为例[J]. 综合运输, 2018, 40 (8): 1-6.

[12] 谭跃进, 吴俊, 邓宏钟. 复杂网络中节点重要度评估的节点收缩方法[J]. 系统工程理论与实践, 2006 (11): 79-83, 102.

[13] 赵志远, 孟相如, 孙瑞男. 基于多属性评估与删除的节点重要度排序方法[J]. 计算机工程, 2018, 44 (6): 62-67.

[14] ALBERT R, JEONG H. BARABASI A L. Error and attack tolerance of complex networks[J]. Nature, 2000, 406 (6794): 378-382.

Optimization of Rail Transit Industry Chain Based on Multi-Layer Complex Networks

XUE Feng1, 2, FAN Qian-li1, LUO Jian3

(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China; 3. School of Automobile and Transportation, Xihua University, Chengdu 610039, China)

With the aim of optimizing the network performance of the rail transit industry chain, in this study, a spatial method was employed to establish the dependency of the rail transit industry chain on the multi-layer complex network topology, and describe the basic structure of the rail transit industry chain. Relevant evaluation indexes were selected, and the performance of the rail transit industry network underattack was analyzed by considering deliberate and random attacks. By using a combination of the entropy weight method and node shrinkage method, the relative importance of nodes and edges, position of key nodes, and change trend of the importance of the key nodes under increasing investment were analyzed. The Chengdu rail transit industry chain was considered as an example to verify the analysis. The results indicate that when multi-layer complex network of rail transit industry chain was attacked, the point played a more important role than the edge in maintaining the stability of the network. With the increase in investment, some nodes, particularly the key nodes, play a significant role in rapidly optimizing the network performance in the short term.

transportation economy; network performance; multi-layer complex network; rail transit industry chain; double-layer network model

1672-4747（2021）02-0065-10

F572.88

A

10.3969/j.issn.1672-4747.2021.02.007

2020-07-14

教育部人文社会科学研究项目（20YJCZH113）；四川省软科学研究计划项目（2021JDR0220）；成都市软科学研究项目（2020- RK00-00108-ZF）

薛锋（1981—），男，汉族，山东邹城人，副教授，研究方向为运输组织理论与系统优化，E-mail：xuefeng.7@163.com

罗建（1982—），女，汉族，重庆璧山人，副教授，研究方向为交通运输规划与管理，E-mail：0120100001@mail.xhu.edu.cn

薛锋，范千里，罗建. 基于多层复杂网络的轨道交通产业链优化[J]. 交通运输工程与信息学报，2021, 19(2): 65-73, 83.

XUE Feng, FAN Qian-li, LUO Jian. Optimization of Rail Transit Industry Chain Based on Multi-Layer Complex Networks [J]. Journal of Transportation Engineering and Information, 2021, 19(2): 65-73, 83.

（责任编辑：李愈）