基于元胞自动机模型的地铁列车折返间隔分析
2021-06-07倪少权吕苗苗
张 海,倪少权,吕苗苗
基于元胞自动机模型的地铁列车折返间隔分析
张 海,倪少权,吕苗苗
(1. 西南交通大学,交通运输与物流学院,成都 611756;2. 综合交通运输智能化国家地方联合工程实验室,成都 611756;3. 综合交通大数据应用技术国家工程实验室,成都 611756)
科学、合理的仿真模型是研究地铁列车折返间隔的关键。本文建立的连续型元胞自动机模型,在参数设置上具有更好的适配性,且能有效缩短步长,以提高仿真精度从而更精确地模拟列车实际运行。该仿真基于列车运行状态,对移动闭塞地铁列车追踪运行及站后折返场景进行了仿真,得到的时间-距离图、距离-速度图及现场实测数据验证了模型的可用性及仿真精度。同时定量分析了道岔侧向限速、列车制动性能、停站时间对折返间隔的影响,提出了缩短折返间隔的措施,使折返间隔降低了31.22%,为提高线路运营能力提供了参考。
铁路运输;折返间隔;元胞自动机;列车运行;运营能力
0 引 言
随着城市轨道交通线网的形成,客流量不断增大,部分城市高峰时段地铁列车追踪间隔已不能满足客流需求。列车追踪间隔由区间追踪间隔、中间站通过间隔和折返站折返间隔组成。根据现有文献[1, 2]及地铁线路实际运营情况可知,折返间隔是制约线路通过能力的限制因素。因此,准确模拟列车追踪运行并寻求缩短折返间隔的措施是提升地铁线路运营能力的关键。
研究列车折返间隔主要有三种方法:解析法、优化法与计算机仿真法。解析法[1-5]通过分析列车折返作业过程及相关影响因素,得出计算折返间隔的数学关系式。解析法对于基于固定闭塞及准移动闭塞信号系统制式下列车追踪间隔计算精度较高,而城市轨道交通移动闭塞制式下列车追踪间隔影响因素较多,依赖的经验公式或简单的理论推导对于计算移动闭塞制式下列车折返间隔存在一定的误差。优化法[6]通过建立列车折返过程中需遵循的各种约束条件,寻求特定目标函数下折返间隔的最优解。优化法求解的是特定目标函数下的折返间隔,得出的折返间隔值与设定的目标函数有关,且不能直观地反映列车实际追踪运行情况,也不便于对折返间隔影响因素进行分析。计算机仿真法[7]通过建立列车折返运行模型,模拟列车折返作业过程,实现折返间隔的快速求解。计算机仿真法根据列车追踪运行规律建立列车折返运行模型,求解效率及精度高,且可直观地反映列车实际追踪运行情况,便于进行折返间隔影响因素分析。故本文研究移动闭塞制式下列车折返间隔及其影响因素,计算机仿真法是较为理想的方法。
对于计算机仿真法而言,既可采用现有的商业软件,也可以建立特定的模型。用于列车运行仿真的商业软件有TPC列车牵引计算系统、UTRAS列车运行仿真系统、Railsys铁路仿真系统、OpenTrack系统等,其局限性在于不适用于我国地铁线路已普遍使用移动闭塞信号系统的实际情况,也不适用于所有特定的列车追踪运行场景,且由于底层代码不公开使研究者不能进行有针对性的二次开发。元胞自动机模型是通过建立特定模型进行列车运行仿真的重要代表,通过局部演化规则模拟出复杂系统的动态行为,如Nagel等[8]于1992年提出Nasch模型用以模拟道路交通。在基于Nasch模型的基础上,Li等[9]建立了基于固定闭塞及移动闭塞的元胞自动机模型,模拟列车追踪运行情况。周华亮等[10]建立了基于准移动闭塞的元胞自动机模型,分析列车延迟传播特性。徐瑞华等[11]建立了列车站前折返元胞自动机模型,模拟地铁列车站前折返过程。侯忠生等[12]建立了基于移动闭塞的元胞自动机模型,提出折返能力是限制城市轨道交通运营能力的重要节点。陈永等[13]提出了考虑线路弯道的元胞自动机模型,研究了弯道半径、外轨超高及弯道长度对线路通过能力的影响。齐姗姗等[14]提出了改进的元胞自动机模型,对速度及位移更新规则进行了修正。Li等[15]建立了加速度时变的元胞自动机模型,对城市轨道交通列车运行曲线及能耗值进行了分析。Becker等[16]建立了列车运行元胞自动机模型,研究了停站时间对列车追踪间隔的影响。以上研究表明元胞自动机模型是进行列车追踪运行研究的有力工具。
针对既有元胞自动机模型的不足,本文建立了连续型元胞自动机模型以更精确地模拟列车实际追踪运行情况,为研究地铁列车追踪间隔提供新的思路。基于该模型对折返间隔影响因素进行定量分析,提出缩短折返间隔的具体措施,为提高线路通过能力提供理论依据。
1 列车追踪场景及折返过程
以某城市地铁线路为例,列车从车站1下行站台出发,在车站2进行站后单线折返。由于折返能力是线路通过能力的制约因素,图1所示轨道线路足以进行列车折返能力及影响因素分析。
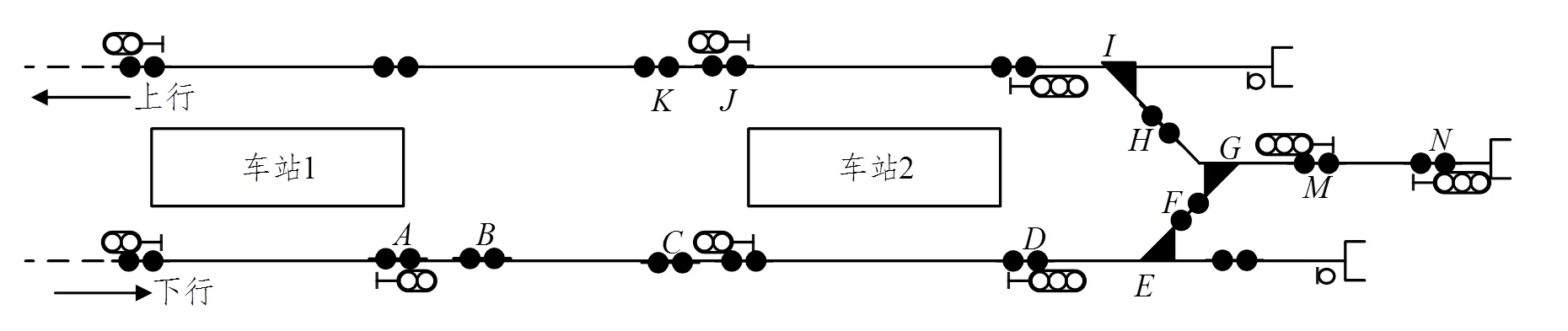
图1 轨道线路布置图
列车在追踪过程中需满足移动闭塞列车最小追踪距离要求,其速度需满足站台限速、道岔限速等要求,后面将进行详细介绍。列车折返过程如下:
(4)列车在车站2上行站台停站时间结束后,驶离上行站台。
2 连续型元胞自动机模型
本文建立的连续型元胞自动机模型实际上是时间离散的列车状态步进模型,其不再基于轨道线路元胞状态,而是基于列车自身状态,为系统内每一列车建立了数组以存储列车的速度、位置、状态信息。将轨道线路元胞长度虚拟为无穷小,列车位置按照实际运行距离进行更新,列车加速度、减速度、站台限速、道岔限速等参数的取值不受限制,可采用实际参数。因其不再存储轨道线路元胞状态,从而释放了计算机内存,减少了计算频次,提高了程序运行效率,为缩短步长创造了条件。


2.1 列车在区段运行(列车出清计轴点)
(1)满足站台限速要求,即列车运行速度不能大于站台限速。
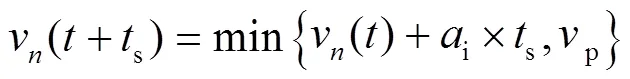
② 其他情况下:
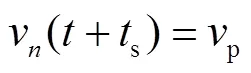
(2)满足列车最小追踪距离要求。若列车与前车的距离小于移动闭塞最小追踪距离则减速,大于最小追踪距离则加速,否则速度不变。


③ 其他情况下:

其中,
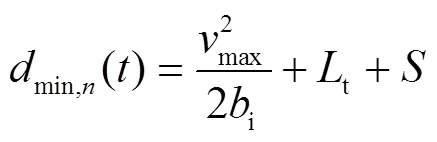
2.2 列车在区段运行
(1)满足列车最小追踪距离要求。


③ 其他情况下:

其中,

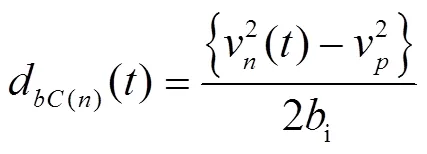
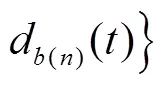
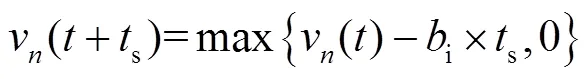
② 其他情况下:

2.3 列车在区段运行
(1)满足站台限速要求。
(2)如果列车到站台停车点的距离小于制动距离,则减速。


③ 其他情况下:
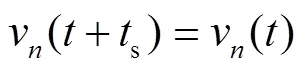
2.4 列车在区段运行


③ 其他情况下:

2.5 列车在区段运行

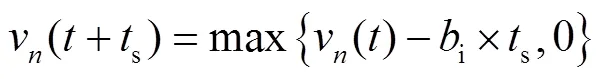
③ 其他情况下:

2.6 列车在区段运行
列车在上述各个区段运行过程中,运行距离单位步长更新一次:
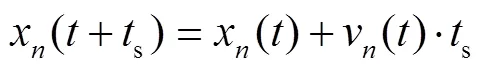
3 实例分析
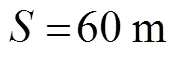

表1 不同速度区间对应的列车加速度值
3.1 折返间隔仿真分析
(1)发车间隔小于折返间隔时
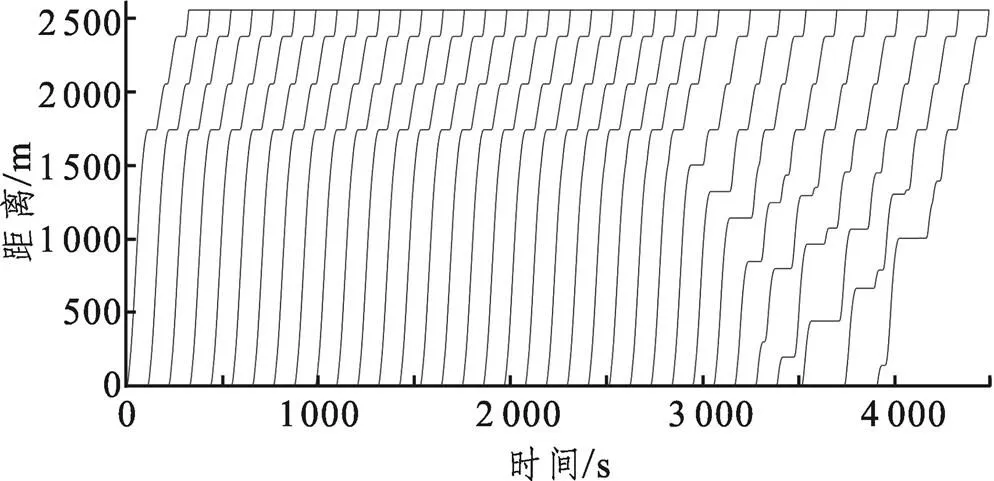
图2 时间-距离图
由仿真结果可知,第27~33列车在区段运行时间分别为:145.23s、195.78s、218.67s、273.55s、320.10s、366.58s、402.31s;第34列车由于不满足移动闭塞列车最小追踪距离要求,在既定发车时间不能发出,第33列车发出后221.83s第34列车才发车。即:当发车间隔小于折返间隔时,折返间隔成为线路通过能力瓶颈,列车在区间运行受到前行列车的影响,且该影响随着发出的列车数量增多而不断增大。仿真结果与列车实际运行情况一致。
(2)逐渐增大发车间隔
(3)将发车间隔调整为折返间隔

时间/s
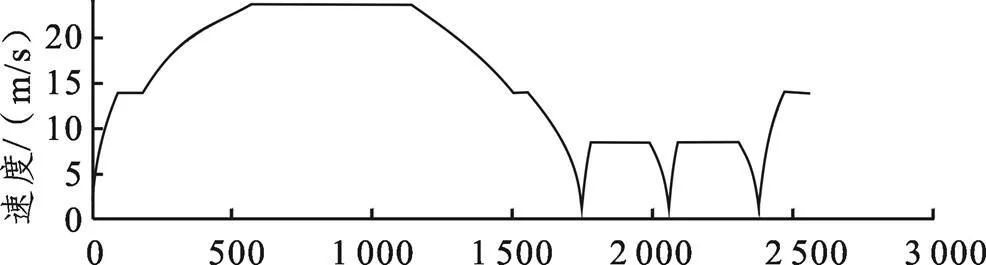
距离/m
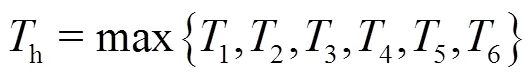

3.2 折返间隔仿真结果验证
在项目现场利用6列电客列车进行折返间隔极限测试,以得出列车实际运行时的折返间隔。进路具备开放条件时,行调立刻手动排列车站2接车进路-及折返轨发车进路-,进路排好后列车按照ATO模式进行自动折返。实测出的列车折返间隔为112.27s。
人工排列进路是ATS系统故障情况下的特殊运营组织模式,正常运营时相关进路通过ATS系统自动触发并排列。为验证ATS自排进路场景下的列车折返间隔,将所测得的112.27s折返间隔编入列车时刻表中,严格遵守折返间隔测试及验收流程进行ATS自排进路场景下的折返间隔测试。测试结果表明列车运行满足112.27s折返间隔。考虑到人工排列进路需要一定的反应时间,ATS自排进路场景下列车最小折返间隔值应略小于112.27s。逐渐调小时刻表中列车折返间隔值,直至观察到列车发生晚点。测试结果为:当折返间隔降低为108.41s时,列车刚好能够按照时刻表进行折返追踪(所有列车均未发生晚点)。现场测试得出结论为:列车在正常运营时折返间隔为108.41s。
本仿真所得列车折返间隔为110.32s,相较于现场实测折返间隔108.41s相差仅1.76%。利用既有元胞自动机模型仿真所得折返间隔为117s,与现场实测值相差7.92%。由此可知,本文所建立的连续型元胞自动机模型可用性及仿真精度优于既有模型,能够用于列车折返间隔方面的研究。
3.3 折返间隔影响因素分析
(1)道岔侧向限速对折返间隔的影响

表2 不同参数下的折返间隔
不同型号道岔允许的侧向过岔速度不同,9号道岔为30 km/h,12号道岔为45 km/h[2]。目前地铁线路普遍使用9号道岔,可使用较大型号的道岔或对9号道岔进行改造,从而缩短折返间隔,提高线路运营能力。
(2)列车制动率对折返间隔的影响
(3)停站时间对折返间隔的影响
基于上述分析可知,可通过提高道岔侧向限速,提高列车制动性能,适当减少停站时间,以减小折返间隔,从而提高线路运营能力。
4 结 论
本文建立了连续型元胞自动机模型,对移动闭塞地铁列车追踪及站后折返运行进行仿真,基于该模型得出了折返间隔压缩措施及压缩效果。
(1)该模型基于列车自身状态,为时间离散的列车状态步进模型。采用线路及列车实际参数值进行仿真,步长从既有模型1s减小为0.01s,在参数适配性及仿真精度上优于既有模型。
(2)不同发车间隔下的仿真结果与列车实际运行情况一致,且仿真所得列车折返间隔值与现场实测折返间隔值相差仅1.76%,验证了该模型的可用性及仿真精度,说明其可用于列车折返间隔方面的研究。
(3)仿真结果表明,通过提高道岔侧向限速和列车制动性能、减少停站时间,在既定参数取值范围内折返间隔可降低31.22%。该模型既可为既有地铁线路折返间隔改造提供理论依据,也可为新建线路列车折返能力检算及相关设备招投标工作提供数据支撑。
(4)由于部分城市地铁线路采用站后双折返轨进行交替折返,下一步将利用连续型元胞自动机模型构建站后双轨折返场景,提出减小折返间隔的具体措施。
[1] 董松. 信号系统提升车站折返能力的研究[J]. 铁道通信信号, 2019, 55(1): 70-74.
[2] 曹宏丽. 城市轨道交通站后折返能力影响分析及优化[J]. 铁道通信信号, 2018, 54(3): 93-95.
[3] 翟恭娟. 城市轨道交通折返站折返能力分析[J]. 交通运输工程与信息学报, 2015, 13(3): 59-63.
[4] 文迪, 倪少权, 李雪婷, 等. 动车组转线折返作业时间计算方法研究[J]. 交通运输工程与信息学报, 2017,15(4): 147-153.
[5] 陈垚, 毛保华, 柏赟, 等. 城市轨道交通多交路模式下中间折返站能力分析[J]. 交通运输系统工程与信息, 2017, 17(3): 150-156.
[6] 江志彬, 饶娅. 多股道城市轨道交通车站站前折返能力分析[J]. 同济大学学报: 自然科学版, 2017, 45(9): 1328-1335.
[7] 陈卫华, 张成国. 保护区段对行车折返效率影响的分析[J]. 铁路计算机应用, 2017, 26(9): 60-63.
[8] NAGEL K, SCHRECKENBERG M. A cellular automaton model for freeway traffic[J]. Journal de Physique I, 1992, 2(12): 2221-2229.
[9] LI K P, GAO Z Y, NING B. Cellular automaton model for railway traffic[J]. Journal of Computational Physics, 2005, 209(1): 179-192.
[10] 周华亮, 高自友, 李克平. 准移动闭塞系统的元胞自动机模型及列车延迟传播规律的研究[J]. 物理学报, 2006, 55(4): 1706-1710.
[11] 徐瑞华, 石俊刚. 基于元胞自动机的列车站前折返仿真模型[J]. 系统仿真技术, 2011, 7(4): 273-278.
[12] 侯忠生, 陈飞. 基于元胞模型的列车运营能力研究[J]. 北京交通大学学报, 2014, 38(2): 29-36.
[13] 陈永, 王晓明, 党建武, 等. 移动闭塞条件下线路弯道对列车交通流影响的研究[J]. 物理学报, 2014, 63(3): 1-11.
[14] 齐姗姗, 彭其渊. 改进的元胞自动机列车交通流仿真模型研究[J]. 计算机工程与应用, 2019, 55(24): 254- 258.
[15] LI W J, NIE L. An improved cellular automata model for train operation simulation with dynamic acceleration[J]. Modern Physics Letters B, 2018, 32(8): 1-12.
[16] BECKER M, SCHRECKENBERG M. Case study: influence of stochastic dwell times on railway traffic simulations[C]// 2018 21stInternational Conference on Intelligent Transportation Systems(ITSC). Hawaii: IEEE, 2018: 1227-1233.
Analysis of Subway Trains’ Turn-back Headway Based on the Cellular Automaton Model
ZHANG Hai, NI Shao-quan, LV Miao-miao
(1. School of Transportation and Logistics, Southwest Jiaotong University, Chengdu 611756, China; 2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu 611756, China; 3. National Engineering Laboratory of Integrated Transportation Big Data Application Technology, Chengdu 611756, China)
A scientific and reasonable model is essential in studying subway trains’ turn-back headway. This paper thus established a continuous cellular automaton model, compared to previous model, this model is more accurate for simulating actual train running by considering actual adaptive parameters’ setting and shortened simulation step-time. This model simulated train tracking and station-behind turning back scenario in a moving block mode based on train running status. Simulation results of the time-distance diagram, distance-speed diagram, and onsite measured value of train turn-back headway verified the availability and the simulation accuracy of this model. In addition, we carried out quantitative analysis of factors influencing turn-back headway such as point area speed restriction, train deceleration rate, and station dwell time, and proposed measures to shorten turn-back headway. With these measures, the value of turn-back headway was reduced by 31.22%, which is an important reference to improve operation capability of the whole line.
railway transportation; turn-back headway; cellular automaton model; train running; operation capability
1672-4747(2021)02-0037-09
U292.5
A
10.3969/j.issn.1672-4747.2021.02.004
2020-09-12
国家重点研发计划资助(2017YFB1200702);国家自然基金项目(61703351,71971182);中国铁路总公司科技研究计划项目(P2018T001,P2018X001,N2018X006-01);四川省科技计划项目(2020YFH0035,2020YJ0268,2020YJ0256,2020JDRC0032)
张海(1986—),男,汉族,四川广安人,博士研究生,研究方向:城市轨道交通运输组织优化,E-mail:zhzxt666666@126.com
吕苗苗(1986—),女,汉族,山西太原人,讲师,研究方向:轨道交通运输组织优化,E-mail:lvmiaomiao@swjtu.cn
张海,倪少权,吕苗苗. 基于元胞自动机模型的地铁列车折返间隔分析[J]. 交通运输工程与信息学报,2021, 19(2): 37-45.
ZHANG Hai, NI Shao-quan, LV Miao-miao. Analysis of Subway Trains’ Turn-back Headway Based on the Cellular Automaton Model [J]. Journal of Transportation Engineering and Information, 2021, 19(2): 37-45.
(责任编辑:刘娉婷)
