Security control of positive semi-Markovian jump systems with actuator faults

Junfeng Zhang · Haoyue Yang · Suhuan Zhang · Xianglei Jia

Abstract Actuator faults usually cause security problem in practice. This paper is concerned with the security control of positive semi-Markovian jump systems with actuator faults. The considered systems are with mode transition-dependent sojourntime distributions, which may also lead to actuator faults. First, the time-varying and bounded transition rate that satisf ies the mode transition-dependent sojourn-time distribution is considered. Then, a stochastic co-positive Lyapunov function is constructed. Using matrix decomposition technique, a set of state-feedback controllers for positive semi-Markovian jump systems with actuator faults are designed in terms of linear programming. Under the designed controllers, stochastic stabilization of the systems with actuator faults are achieved and the security of the systems can be guaranteed. Furthermore, the proposed results are extended to positive semi-Markovian jump systems with interval and polytopic uncertainties. By virtue of a segmentation technique of the transition rates, a less conservative security control design is also proposed. Finally,numerical examples are provided to demonstrate the validity of the presented results.

Keywords Positive semi-Markovian jump systems · Sojourn-time distribution · Actuator faults · Linear programming

1 Introduction

Markovian jump systems are a class of stochastic hybrid systems. There are many applications in practice such as network control systems [ 1- 3], power systems [ 4, 5], and multi-agent systems [ 6, 7]. Positive Markovian jump systems are a special kind of Markovian jump systems in which all subsystems are positive. Some eff orts have been devoted to positive Markovian jump systems. In [ 8],l1-gain performance analysis and mode-dependent controller design were addressed for positive Markovian jump systems with time-delay. A suffi cient condition for the existence of the desired positivel1-gain f ilter was established in [ 9]. Using a linear co-positive Lyapunov function, a positivel1statebounding observer for positive T-S fuzzy Markovian jump systems was designed in [ 10]. A state-feedback controller was constructed for positive Markovian jump systems with time-varying and partly known transition rates using appropriate co-positive type Lyapunov function [ 11]. More results can be found in [ 12- 17] and references therein. It should be pointed out that the transition rates of Markovian jump systems in the above results are always considered to be constant. However, in practical applications, the transition rates of many jump systems are time-varying due to the complexity of the environment [ 18, 19]. The sojourn-time of transition rates follows a non-exponential distribution. Such systems are referred to as semi-Markovian jump systems.In recent years, control synthesis of semi-Markovian jump systems have attracted much attention. Some fairly valuable achievements have been reported in [ 20- 27]. To mention a few, an expected reliable f ilter for a semi-Markovian jump time-delay system with parameter uncertainties was designed by virtue of an improved mutual convex approach incorporated with a new integral inequality [ 20]. In [ 21], the inf initesimal operator of the constructed Lyapunov function was derived for the f irst time and the robust control problem for semi-Markovian jump systems with norm-bounded uncertainties was discussed. By introducing semi-Markovian kernel approach, the literature [ 22] proposed a new stability notion that generalizes the traditional mean-square stability.However, these results on semi-Markovian jump systems are only applicable to the situation where the sojourn-time distribution does not depend on mode transition. Therefore,to relax this restriction, semi-Markovian jump systems with mode transition-dependent sojourn-time distributions needs to be explored.

On the other hand, in most of the results described above,the actuator of the system is considered to be normal. In fact,the actuators of the system may fail due to various complicated and unexpected factors. Such faults might cause instability of systems and induce the security risk of systems.There have been some results concerning actuator faults in the general case (not necessarily for positive systems).In [ 28], a hybrid state-feedback strategy was redesigned to guarantee exponential stability of the system by choosing a appropriate Lyapunov-Krasovskii functional and using the linear matrix inequality technique. An adaptive sliding mode controller that can estimate the online eff ectiveness loss of actuator faults and the bounds of nonlinear terms and external disturbances was designed in [ 29]. A new generalized fuzzy sliding mode observer approach was presented to estimate system states, sensor and actuator fault vectors[ 30]. By constructing an appropriate Lyapunov-Krasovskii functional, a set of robust fault-tolerant controllers ensuring robust stochastic stabilization of systems were designed based on linear matrix inequality formulation [ 31]. More results on actuator faults can be found in [ 32- 36]. To the authors best of knowledge, there are no achievements in the security control of positive semi-Markovian jump systems with actuator faults. By the above observation, most results on actuator faults of semi-Markovian jump systems were obtained by adopting the quadratic method based on linear matrix inequality. However, due to the property of positive systems, the quadratic method can not be directly applied.As a result, some questions naturally arise: how to establish a frame of security control for positive semi-Markovian jump systems with mode transition-dependent sojourn-time distributions and how to establish a controller fault model for positive semi-Markovian jump systems with mode transition-dependent sojourn-time distributions? These questions are full of challenges and motivate us to carry out this work.

In this paper, the control synthesis of positive semi-Markovian jump systems with actuator faults is studied under mode transition-dependent sojourn-time distributions. First, a stochastic co-positive Lyapunov function is constructed. The inf initesimal operator of the established Lyapunov function is derived in the case where the distribution of sojourn-time depends on the mode transition. Then, a family of state-feedback controllers with a fault model for system under consideration are designed. Under the designed controllers, the resulting closed-loop system is positive and stochastically stable.Furthermore, we discuss the robust stochastic stabilization of positive semi-Markovian jump systems with interval and polytopic uncertainties. The presented suffi cient conditions for ensuring the robust stochastic stability of the resulting closedloop systems are solvable in terms of linear programming.Finally, a segmentation technique of the transition rates is presented to reduce the conservation of the stability conditions for the resulting system. The reminder of the paper is organized as follows. Section 2 gives the system model description and preliminary knowledge. Stochastic stabilization and robust stochastic stabilization of the systems with interval and polytopic uncertainties are proposed in Sect. 3. Section 4 provides numerical examples to illustrate our design. Finally, Sect. 5 concludes the paper.

2 Problem formulation

Consider a class of semi-Markovian jump systems:

whereγij＞0 andβij＞0 are scale parameter and shape parameter, respectively. For convenience of later derivation,the distribution functionsFii(h) andfii(h) are def ined by mode transition and are more suitable for describing the Markovian process of the systems with actuator fault phenomena.

Now, we introduce some def initions and lemmas on positive systems, which can be found in [ 38- 41] for details.

Def inition 1 [ 38, 39] System ( 1) is said to be positive if its state satisf iesx(t)≥0 for any nonnegative initial state and input.

Lemma 1[38,39]System(1)is positive if and only if Ai is a Metzler matrix and Bi≥0for each i∈S.

Lemma 2[40]A matrix A∈ℝn×n is Metzler if and only if there exists a positive scalar λ such that A+λI≥0.

whereqijis the probability intensity from modeitoj. Thus,we have the transition rate functionπij(h):

For system ( 1), we consider the following state-feedback controller:

whereKiis a gain matrix to be designed. The actuator fault model is described as

whereGiis a diagonal fault matrix fori∈J. The fault matrix is unknown and satisf ies

The objective of the paper is to design controller gain matricesKito ensure the positivity and stochastic stability of system ( 1). A system is in the risk of security when the system is subject to actuator faults. The security control of system ( 1) is to design a control law ( 8) such that system( 1) can keep its performance though the system is subject to actuator faults.

3 Main results

In this section, we f irst consider the security control of system ( 10). Then, the security control of system ( 10) with interval and polytopic uncertainties is investigated.

Theorem 1If there exist constants η＞0,λi＞0andℝn vectors vi≻0,ζiι≺0,ζi≺0such that the inequalities

By ( 11b) and ( 15),

Remark 3In [ 8- 14], the stability, stabilization, and performance analysis of positive Markovian jump systems have been explored. In these literature, it is assumed that the transition rates of the systems are always constant and the sojourn-time of the transition rates is subject to exponential distribution. Naturally, these literature cannot handle the case that the transition rates are subject to some functions or the sojourn-time is non-exponential distribution. In practice, the transition rates of many jump systems are timevarying due to unexpected environment factors and ageing of component and mechanical wear [ 18, 19]. Such systems can be described via semi-Markovian jump systems, which are more general than Markovian jump systems. Thus, Theorem 1 is more general than those results in the literature.

Remark 4In a real system, some unexpected security risk may arise due to various external factors that can destroy the performance of the system. For example, due to the open network links among sensors, controllers and actuators, the exchanged data can be easily exploited by adversaries in the networked scenario. A so-called security control is proposed for diff erent possible factors to prevent the occurrence of undesirable situations. Up to now, some results on the security control have been published in [ 43- 45]. Actuator fault is a universal phenomena owing to the degeneration of components and other unexpected factors. Actuator fault also induce the security risk of the system. It is necessary to adopt some control strategies to guarantee the safety of the system. Theorem 1 considers the security control of the systems with actuator faults. It is worthy pointing out that the Weibull distribution used in this paper is popular for describing the behavior of actuator faults. Together with the statements in Remark 3, semi-Markovian jump systems are suitable for modeling some practical systems with actuator faults. Therefore, the systems in this paper is more general than those ones in [ 8- 14]. Meanwhile, Theorem 1 is more practical than the results in the literature.

Remark 5In [ 42], the control synthesis of positive semi-Markovian jump systems was studied without considering actuator faults. As mentioned in the Introduction, the occurrence of actuator faults may cause instability of the systems and aff ect the security of the systems. Therefore, Theorem 1 in this paper further considers the actuator fault problem for positive semi-Markovian jump systems and enhances the stability and security of the systems. On the other hand, the cumulative and probability distribution functions in ( 3) and( 4) are mode-dependent while these functions in [ 42] are independent on the mode. Thus, the cumulative and probability distribution functions in [ 42] are a special case of( 3) and ( 4).

The rest of the proof can be obtained using a similar method to that in Theorem 1.

◻

Next, we discuss robust stochastic stabilization of system ( 10) with polytopic uncertainty. Assume that the system matrices satisfy the following uncertainty sets:

The rest of proof can be given using a similar method to that in Theorem 1 and is omitted.

◻

Remark 6In [ 21], the robust stabilization issues of semi-Markovian jump systems (non-positive) with uncertain parameters has been investigated using quadratic Lyapunov function cooperated with linear matrix inequality. Due to the property of positive systems, the quadratic approach is not effi cient enough for dealing with the robust stabilization problems of positive semi-Markovian jump systems. Using the quadratic approach to deal with positive systems may not only fail to guarantee the positivity of the system, but also cause heavy computational burden. Therefore, Theorems 2 and 3 in this paper propose a new linear programming approach to handle the robust stabilization of positive semi-Markovian jump systems.

By ( 47c) and ( 49),

The rest of the proof can be given using a similar method to that in Theorem 1 and is omitted.

◻

Remark 7Compared ( 47a) with ( 11a), the former uses the upper bound of each segmentation section while the latter uses the upper bound of the transition rates function. The former is less conservative than the latter. From ( 49), each segmentation section has its own controller. Based on these points, this segmentation technique not only reduces the conservatism of the stability conditions but also accelerates the stability of the systems.

Theorem 4 only applies the segmentation technique to system ( 10) without uncertain parameters. By virtue of the approach in Theorem 4, it is not hard to extend the segmentation technique to system ( 10) with uncertainties.

Remark 8From ( 12), (30), (39), and ( 48), it is clear that the controller gain matrices are decomposed into the sum of several matrices. Such a design approach is proposed based on a simple matrix decomposition approach. Theorems 1,2, and 4 decompose the controller gain matrices based on the row vectors of the matrices while Theorem 3 is based on the elements of the matrices. Indeed, the two approaches are same. It implies that the matrix decomposition can be carried out not only for row vectors of a matrix but also for elements of a matrix. All of them are suitable for the controller design of positive systems. Under these controllers,the corresponding positivity and stability conditions can be easily transformed into linear programming. These conditions have simple form and lower computation burden. It has been verif ied that linear programming is more eff ective for positive systems than other approaches in [ 8- 16].

4 Numerical examples

In this section, we provide three examples to illustrate the eff ectiveness of the obtained results.

Example 1In [ 16], a virus mutation treatment model was established. Following the model in [ 16], a positive semi-Markovian jump system model was considered in [ 42]:

Fig. 1 Simulations of the state x( t) under the jumping signal r( t) in[ 42]

Fig. 2 Simulations of the state x( t) with actuator faults in [ 42]

ChooseG1=diag{0.35,0.51},G2=diag{0.56,0.47}. Fig. 4 shows the simulation results of the statex(t) under the jumping signalr(t).

Remark 9By the design in [ 42], Fig. 1 shows the state simulations of system ( 58). When the actuator faults occur, it is shown that the design in [ 42] is failed (see Fig. 2). By

Theorem 1 in this paper, Fig. 4 is given. It is clear that the system is positive and stable regardless of actuator faults.This implies that the presented design approach in Theorem 1 improves the one in [ 42].

Fig. 3 Simulations of transition rates πij(h) , probability distribution function fij(h) , and cumulative distribution function Fij(h) . a π11(h) , f11(h) ,and F11(h) . b π12(h) , f12(h) , and F12(h) . c π21(h) , f21(h) , and F21(h) . d π22(h) , f22(h) , and F22(h)

Example 2Consider the interval system (10) with

Fig. 4 Simulations of the state x( t) under the jumping signal r( t)

Figures 5, 6 and 7 show the simulations of the states and their upper and lower bounds. From the simulation results, it can be seen that the states of system ( 10) always run between the upper and lower bounds until 0. This verif ies that the design in Theorem 2 is eff ective.

Fig. 5 Simulations of the states x1(t),x1(t),x1(t) under the jumping signal r( t)

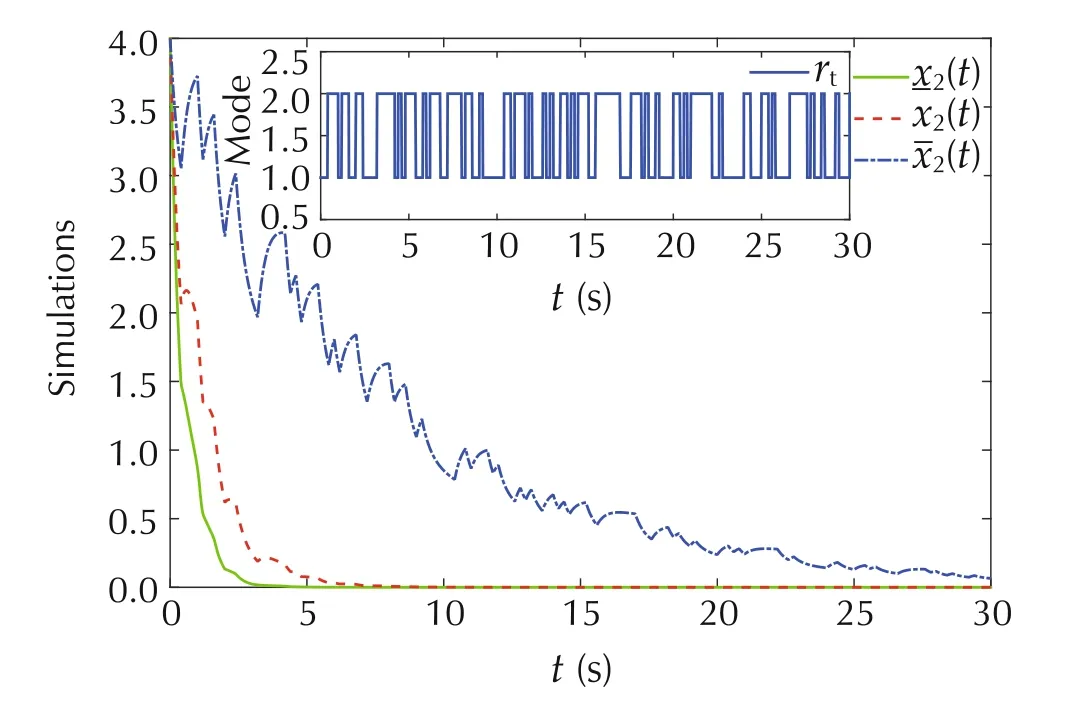
Fig.6Simulations of the states x2(t),x2(t),x2(t) under the jumping signalr( t)

Example 3Consider system ( 10) with two modes. To illustrate the eff ectiveness of the proposed segmentation technique in Theorem 4, the system matrices are chosen as follows:

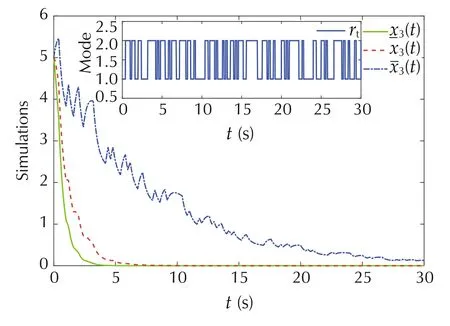
Fig. 7 Simulations of the states x3(t),x3(t),x3(t) under the jumping signal r( t)

Thus,Ai+BiKi,sis a Metzler matrix for eachi∈J,s=1,2 .In addition, we choose the same system parameters as above.The upper and lower bounds ofπij(h) are the same as those ones in Example 1. Figure 8 shows the simulation results of the states obtained from Theorems 4 and 1, respectively.It can be found that the use of transition rate segmentation technique can accelerate the convergence rate.

5 Conclusions and further work

This paper has investigated the security control problem of positive semi-Markovian jump systems with mode transition-dependent sojourn-time distributions. First, the stochastic stabilization issues of the considered systems with actuator faults are achieved by constructing a stochastic co-positive Lyapunov function. Using matrix decomposition technique and linear programming approach, a family of state-feedback controller with an actuator fault has been designed. Then, the robust stochastic stabilization problem of positive semi-Markovian jump systems with interval and polytopic uncertainties has been solved. Finally, a transition rate segmentation technique that reduces the conservativeness of the stability conditions for the resulting closed-loop system has been proposed.

Fig. 8 Comparisons of Theorems 4 and 1

In future work, it may be interesting to develop the proposed approach for positive semi-Markovian jump systems with f ilter and sensor faults, respectively. In addition, it is challenging but interesting to consider positive semi-Markovian jump systems with intermittent fault of actuator and/or sensor.

AcknowledgementsThis work was supported by the National Nature Science Foundation of China (Nos. 62073111, 61703132), the Fundamental Research Funds for the Provincial Universities of Zhejiang (No.GK209907299001-007), the Natural Science Foundation of Zhejiang Province, China (No. LY20F030008), the Foundation of Zhejiang Provincial Education Department of China (No. Y202044335), and the Graduate Scientif ic Research Foundation of Hangzhou Dianzi University (No. CXJJ2020051).