Dynamic output feedback stabilization of deterministic f inite automata via the semi-tensor product of matrices approach

Roozbeh Abolpour · Mohsen Raji · Parisa Moradi

Abstract This paper deals with the dynamic output feedback stabilization problem of deterministic f inite automata (DFA). The static form of this problem is def ined and solved in previous studies via a set of equivalent conditions. In this paper, the dynamic output feedback (DOF) stabilization of DFAs is def ined in which the controller is supposed to be another DFA. The DFA controller will be designed to stabilize the equilibrium point of the main DFA through a set of proposed equivalent conditions. It has been proven that the design problem of DOF stabilization is more feasible than the static output feedback (SOF)stabilization. Three simulation examples are provided to illustrate the results of this paper in more details. The f irst example considers an instance DFA and develops SOF and DOF controllers for it. The example explains the concepts of the DOF controller and how it will be implemented in the closed-loop DFA. In the second example, a special DFA is provided in which the DOF stabilization is feasible, whereas the SOF stabilization is not. The f inal example compares the feasibility performance of the SOF and DOF stabilizations through applying them to one hundred random-generated DFAs. The results reveal the superiority of the DOF stabilization.

Keywords Discrete event dynamic system · Finite automata · Dynamic output feedback stabilization · Semi-tensor product

1 Introduction

Deterministic finite automaton (DFA) is a finite-state machine that smartly responses to a set of events or symbols.DFAs consist of states, events, and outputs that can be f inite logical or discrete sets [ 1]. DFA is the most popular kind of f inite automata (FA) that has known and deterministic behaviors [ 2]. This machine is frequently addressed in the literature due to its capability to model the discrete event systems [ 2]. Diff erent kinds of this machine are developed in various practical and theoretical applications [ 3, 4].

A logical network is a discrete-time system in which the state, input, and output vector admits only f inite levels [ 5].DFAs can be conceptually included in logical networks because its state, input, and output vectors similarly admit f inite levels. A Boolean network f irstly developed by Kauff -man [ 6] is another kind of logical networks in which state,input, and output vectors only support two levels [ 5]. Furthermore, logical networks are widely exploited to model the other applications involving game theory [ 7], system biology[ 6] and digital circuits [ 8].

The stability of DFAs is recently def ined and investigated in previous studies [ 2, 9]. Several def initions are provided for DFA stability involving Lyapunov stability and asymptotic stability based on Lyapunov functions [ 2]. DFA is modeled by a set of symbols (states, inputs, and outputs) and some transition functions in the theoretical computer topics [ 10].The ineffi ciency of this model for presenting the stability and stabilizability concepts is one of the most important issues arising in this topic [ 10]. To cope with this issue, the semitensor product (STP) is frequently and widely exploited to model DFAs, see, e.g., [ 10] and [ 11]. This mathematical tool results in a matrix-based model which is more attended in the control topics [ 11]. It should be noted that this tool is widely used to model various systems such as fuzzy control systems [ 12], Boolean control networks (BCNs) [ 13],networked evolutionary games [ 7], nondeterministic f inite automata [ 14] and discrete event systems [ 15].

Output stabilization of DFAs along with partial observations is another important issue in this regard [ 16]. It means the controller cannot explicitly use the current DFA’s states due to their immeasurability assumption. There exists a set of output symbols which are attached to DFA’s states and used by the controller. In general, an output feedback controller can be considered as static or dynamic [ 16].

In the static output feedback (SOF) controller, the control law is supposed to beu(t)=Ky(t) in whichKis a constant feedback gain matrix that should be precisely determined to stabilize the DFA [ 16]. Ozveren proposes a necessary and suffi cient condition to explore the existence of an appropriate constant feedback gain matrix for stabilizing the closedloop DFA [ 9]. It is worth mentioning that the other controllers are also developed to optimally control the behaviors of the closed-loop DFA. For instance, the time-invariant output feedback (TIOF) [ 10] and the time-varying output feedback(TVOF) [ 10] controllers are applied to BCNs which can be conceptually included in DFAs [ 10].

The stability and stabilizability problems of logical networks such as Boolean networks have been widely investigated in previous studies [ 15- 21]. It has been reported that these problems are naturally NP-hard which means their feasibilities cannot be investigated by polynomial-time algorithms [ 5]. The STP method plays a key role to develop stability and stabilizability conditions for both logical and Boolean networks [ 17]. Through this method, the dynamical behaviors of logical networks can be expressed by a convenience state matrix structure. Therefore, classical approaches such as Lyapunov theory can be exploited to evaluate the stability of these networks.

The Lyapunov theory was utilized by recent studies to develop stability conditions for logical or Boolean networks[ 18- 20]. Meng et al. used the concept of positive systems,l1gain analysis and Markovian jump parameters to investigate the stability of Boolean networks based on the Lyapunov theory [ 18]. Possieri and Teel focused on the asymptotic stability analysis of stochastic Boolean networks and proposed a Lyapunov-based method for this purpose [ 19]. Li and Ding extended the Lyapunov theory to the stabilizability problem of logical control networks and proposed novel theoretical results in this regard [ 20].

Pinning control strategy is another approach that was proposed to solve the stabilization problem of Boolean networks[ 21]. In this strategy, some control inputs are added to the main system for controlling a group of its states [ 22]. In fact, some states are controlled and the rest freely propagate based on the existed coupling between the states. Li[ 23] forced the designed pinning controllers to have state feedback form to establish common controllers. Lu et al.focused on the number of required controllers in this strategy and developed a controller with minimum number of controllers [ 21].

Previous approaches have several drawbacks such as the conservativeness and the simple structure of controllers.These drawbacks can signif icantly inf luence the controller performance such as its stability. To cope with these issues,a more complicated controller is required to enhance the conservativeness of this design problem.

In this paper, dynamic output feedback (DOF) stabilization of DFAs is def ined to establish the stability of the equilibrium state. Def ining a DOF controller and developing a suffi cient and necessary condition to check its feasibility are the main aims of this paper. At f irst, STP modeling idea is exploited to model the behavior of DFAs. In the second step,the proposed DOF, which is brief ly another DFA, is def ined for stabilizing the original DFA. Finally, the design problem of a DOF will be equivalently solved by a set of proposed conditions. The proposed approach has some important advantages as follows:

· The designed DOF controller may have f lexible and free structure; i.e., it can consist some known and unknown(free variable) parameters.

· It is proved that the DOF design problem is more feasible than the SOF design problem.

· A condition is developed to equivalently assess the existence of a feasible DOF controller.

· An algorithm is designed to obtain the DOF controller based on the proposed condition.This paper is organized as follows. Section 2 presents some basic notations and preliminaries to propose the main contributions of this paper. Section 3 presents the main results of this paper involving the DOF def inition and its related theorem. In Sect. 4, three examples are provided to reveal the theorems, explain the implementation details of the DFA controller, and compare the feasibility performances of the SOF and DOF controllers. Finally, Sect. 5 concludes the paper.

2 Preliminaries

This section brief ly presents some preliminaries shown in Table 1, which are needed to propose the main contributions of this paper.

2.1 DFA def initions

Definition 1 A DFA is a six-tupleG=(X,E,Y,f,h,x0) ,in whichX=x1,…,xn,E=e1,…,em, andY=y1,…,ypare the sets of states, input symbols (events), and outputs,respectively;x0∈Xis the initial state;f∶X×E→Xandh∶X→Yare transitions and output functions.

Table 1 Basic notations

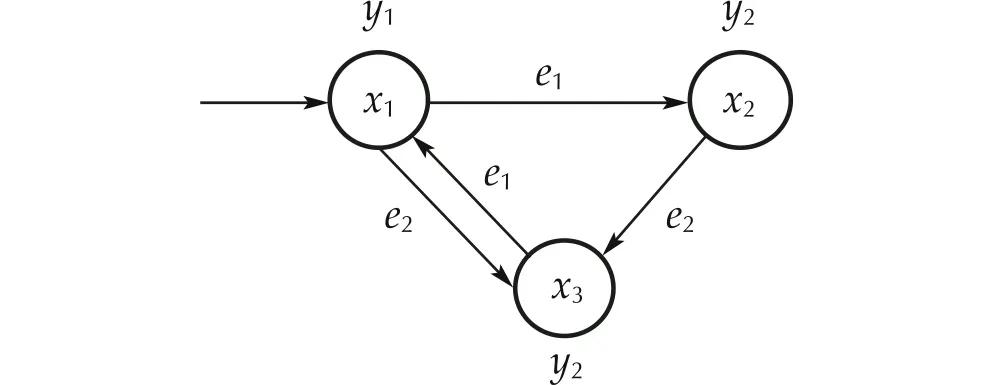
Fig. 1 DFA 1

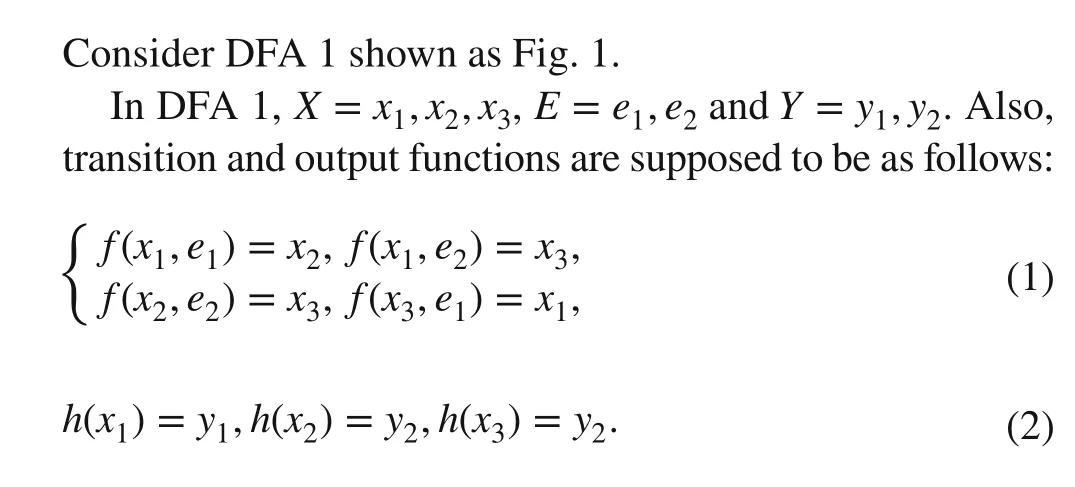
Def inition 2 AssumeA∈ℝc1×c2 andB∈ℝd1×d2 . Then, their STP is denoted byA⋉Band def ined with the following equation:

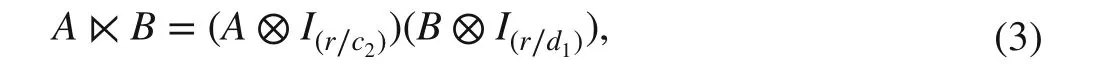
where⊗is the Kronecker product.

Remark 1[ 24] STP has the following properties:

Def inition 3 [ 24] The statexe∈Xis said to be an equilibrium state if there existse∈Esuch thatf(xe,e)=xe.

In fact, statexeis the equilibrium state if there exists a self-path for this state in the DFA. The stability of this equilibrium state is formerly def ined in paper [ 14]. This def inition depends on the DFA’s trajectories, transitions and control laws which is not conventional in control topics.Hence, Def initions 4 and 5 def ine the potential stability that is independent of the control law.

Def inition 4 Statex∈Xis said to be potential stable with respect to the equilibrium statexe∈Xif there exists a f inite path fromxtoxein the DFA.

Def inition 5 [ 24] An equilibrium state is potential stable if all states are potential stable with respect to that equilibrium state, in the DFA. Furthermore, a control law or controller is said to stabilize the equilibrium state if it forces all possible trajectories of the DFA to arrive at the equilibrium state and stay there forever.

To completely understand the above def initions, Fig. 2 shows an instance DFA that is noted by DFA 2. Obviously,this DFA has two equilibrium statesx1andx2. Firstly, the potential stability ofx1is investigated as follows:

wherexi→ekxjmeansxj=f(xi,ek).

Using ( 4),x1is potential stable. Then, the potential stability ofx2is investigated as follows:

Regarding ( 5),x2is potential stable, too.

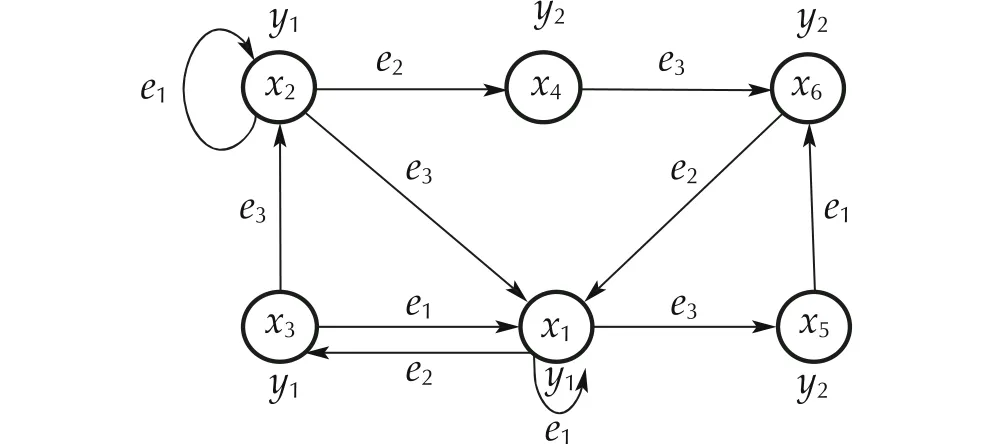
Fig. 2 DFA 2

It must be emphasized that potential stability is a necessary condition for the DOF stabilizability of a DFA.

2.2 State space expression of DFA’s dynamics

whereu(t) is the mapped input vector of the DFA which will be insideΔm. MatrixF∈Mn×nmmaps the transition functionf[ 26].

Similarly, the outputs functionhcan be mapped to the matrixH∈Np×nwhich implies the following equation [ 24]:

wherey(t) is the mapped output vector of the DFA.

Lemma 1Assume i∈1,…,n and k is an arbitrary positive integer number.Then,the k th possible state set can be obtained as follows:

The possible state set is basically used to check the potential stability of an equilibrium state. Lemma 2 exploits this concept to investigate the stability of the equilibrium state.

Lemma 2[27]Assume xe is an equilibrium state of the DFA.xe is potential stable if and only if the following conditions hold:

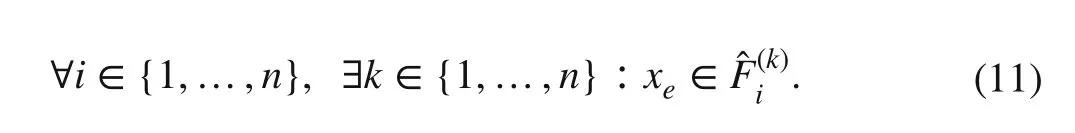
3 Main results

In this section, the main contribution of this paper is presented involving a method to design a dynamic output feedback controller for a DFA. At f irst, the static and dynamic controllers are def ined based on the notations mentioned in the previous section. Then, the proposed method is presented to the design DOF controller.

Note that, the input vector should be lonely depend on the output vector in each step. Indeed, the controller depends on the output vectory(t) and it cannot explicitly utilized the state vectors. Thus, input vectoru(t) should satisfy the following condition:

whereK∈Mm×pis the gain matrix that should be properly designed.

Considerxeis an arbitrary equilibrium state in the DFA.Lemma 3 proposes a set of necessary and suffi cient conditions to check the stabilizability of the equilibrium state with respect to control law ( 13) and Def inition 5.

Lemma 3[24]Assume xe is an equilibrium state of the DFA.Static gain matrix K∈Mm×p stabilizes xe if and only if the following conditions are satisf ied:

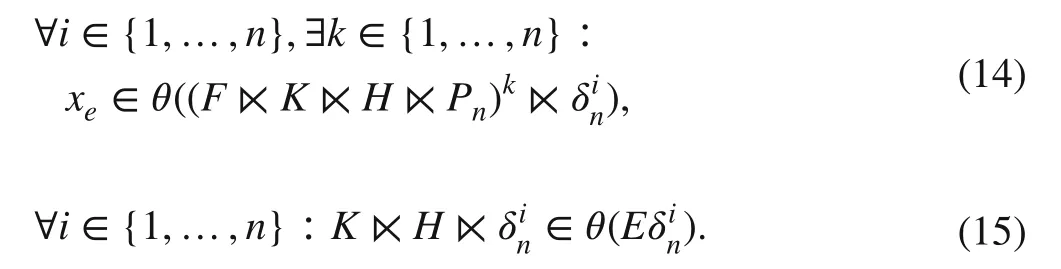
Based on Lemma 3, the static gain matrixKcan be easily obtained via checking all possible matrices inMm×pto satisfy conditions ( 14) and ( 15). If there existsK∈Mm×pthat satisf ies the mentioned conditions, it will be considered as the static gain matrix of the controller.

The structure of the proposed controller is presented as follows:

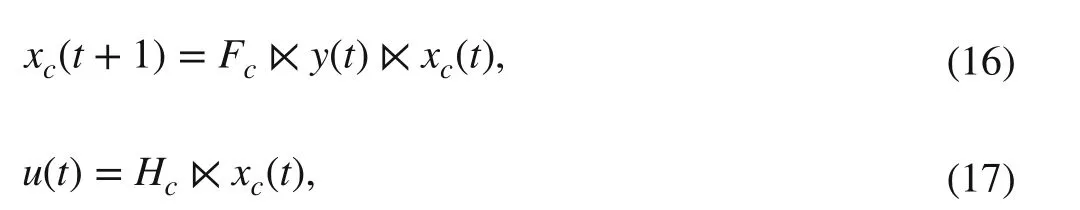
wherexc(t)∈M(nc)is the internal state vector andncis its order.

Indeed, the controller is another DFA withncinternal states such thaty(t) andu(t) are its output and input vectors,respectively. MatricesFc∈Mnc×pncandHc∈Mm×ncare free matrices that should be designed to stabilize the equilibrium sate in the closed-loop DFA.

Remark 2The internal states of the DFA controller may or not have any practical or physical meaning. This fact is the same as the concept of dynamic output feedback stabilization problems of physical systems in which the internal states may be totally virtual signals.

Theorem 1 proposes a set of suffi cient and necessary conditions to check the stabilizability of an equilibrium state in the closed-loop DFA.

Theorem 1Assume xe is an equilibrium state of the DFA.Matrices Fc∈Mnc×pnc and Hc∈Mm×nc stabilize xe if and only if the following conditions hold for all i∈{1,…,n}and j∈{1,…,nc}:

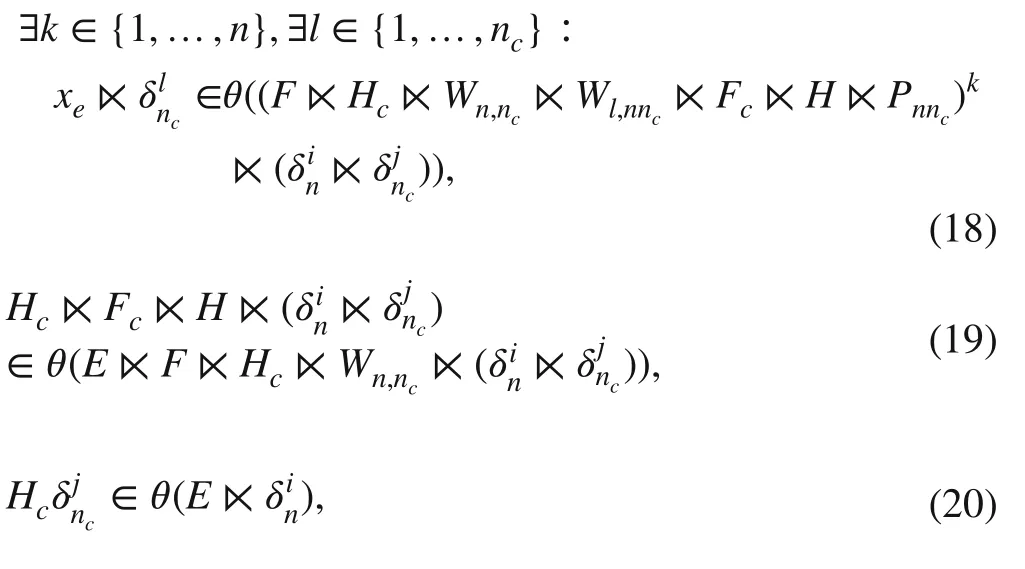
where l is the length of vector FC⋉H⋉δ1nnc.

Using property 6 in Remark 1, the following equation will be obtained:

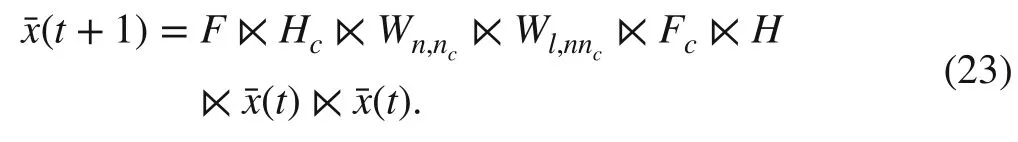
Regarding item 5 in Remark 1, equation ( 23) can be rewritten as follows:

Using ( 27), condition ( 19) will be satisf ied which terminates the proof.

◻

Theorem 2 proves that if a feasible SOF controller exists,then there should be a DOF controller that stabilize the equilibrium state, as well. Indeed, this theorem shows that the DOF stabilization is less conservative than the SOF one.

Theorem 2Assume xe is an equilibrium point and there exists static gain K∈Mm×p that stabilizes xe in the closedloop DFA.Then,there exists an DOF controller with ordernc≥n that stabilizes xe in the closed-loop DFA.

Using ( 29), the model’s dynamics ( 16) and ( 17) will lead to

According to ( 33), the dynamic controller has the same input vector as the static controller. Hence, if the static controller is able to stabilizexe, the dynamics’ controller will be capable, as well.

◻

The steps of the design algorithm are listed below:

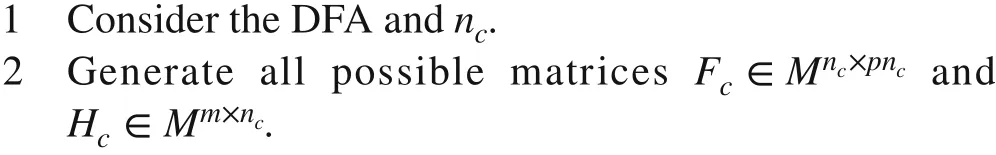
Design algorithm 3 If there exists a pair (Fc,Hc) in the generated matrices that satisfy conditions ( 18), ( 19) and ( 20), return it as the solution of the design algorithm.

4 Otherwise, return the DFA is not dynamically stabilizable and terminate.

Remark 3The number of internal statesnccan aff ect the computation burden of the design algorithm that is presented in Theorem 1. In fact, it is necessary to f ind an appropriate DFA controller with minimum number of internal states.For this purpose, one can repeatedly implement Theorem 1 for a sorted set of state numbers to f ind the minimum one.

Remark 4It is worth mentioning that the static and dynamic stabilizability def initions are equivalent. In both, the stability of a DFA means all trajectories (that are consistent with their corresponding control laws) of the DFA arrive at the equilibrium point and stay there forever.

Remark 5The number of internal statesncis supposed to be greater than the number of the main DFAnin Theorem 2.This condition is considered to prove the better feasibility of the DOF stabilization problem in comparison to the static one. In fact, this condition is not a necessary condition for the feasibility of the DFA controller and it is possible to develop a DFA controller withnc＜nfor some DFAs such as presented in the next section.

4 Illustrative examples

Figure 4 shows the whole possible runs of the DFA considering the above static gain matrix. Figure 4 demonstrates the static gain matrix ( 35) stabilizes the equilibrium statex1. In this f igure, the gray- f illed circles indicate the current state of the DFA at each time step.

Fig. 3 DFA def ined in Example 1

It should be noted that there is no feasible static gain matrix in this DFA. To prove this claim, Figs. 13 and 14 show runs of the DFA for diff erent initial states and all possible static gain matrices.

Fig. 5 Designed controller for DFA def ined in Example 1

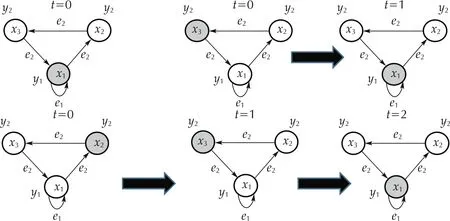
Fig. 4 DFA’s runs of DFA Example 1 for diff erent initial states and evaluating SOF ( 35)

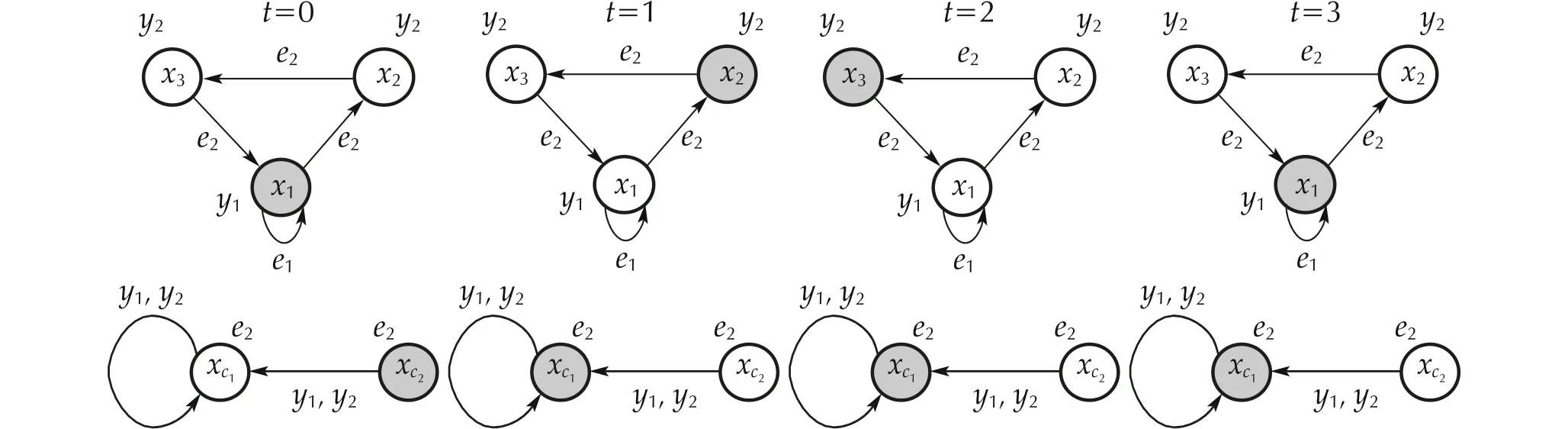
Fig. 7 DFA’s run for DFA in Example 1 considering x(0)=δ31 and xc(0)=δ22 and applying DFA controller ( 36)

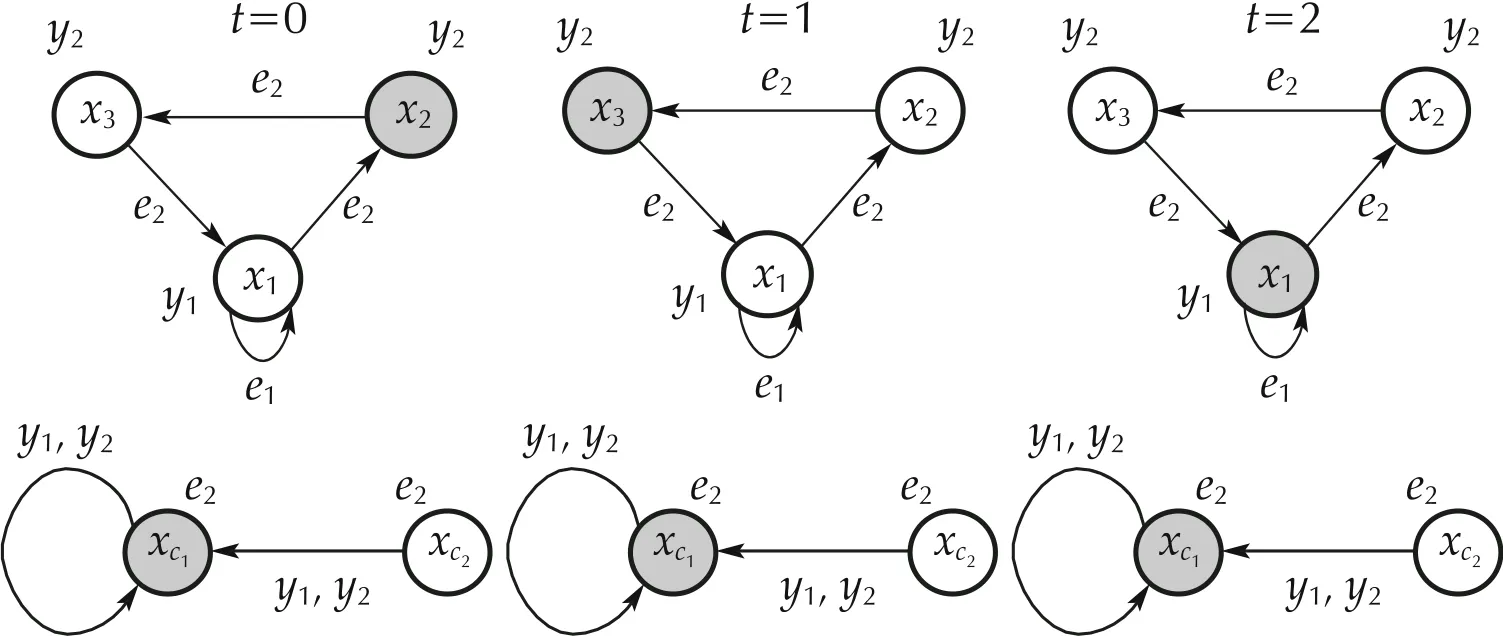
Fig. 8 DFA’s run for DFA in Example 1 considering x(0)=δ32 and xc(0)=δ21 and applying DFA controller ( 36)

Figures 13 and 14 ensure there is no static gain matrix that is capable to stabilize the DFA. Hence, the proposed design algorithm is applied to this DFA to obtain the DFA controller.Equation ( 38) presents the matrices of the DFA controller:The controller is the same as obtained in Example 1 given in Fig. 5. In the sequel, Figs. 15, 16, 17, 18, 19, 20 show all possible runs of the closed-loop DFA. Figures 15, 16, 17,18, 19, 20 exhibit that the proposed controller stabilizes the DFA, whereas there is no feasible static controller. Therefore,this example shows the less conservativeness of the dynamic stabilizability problem in comparison to the static one.

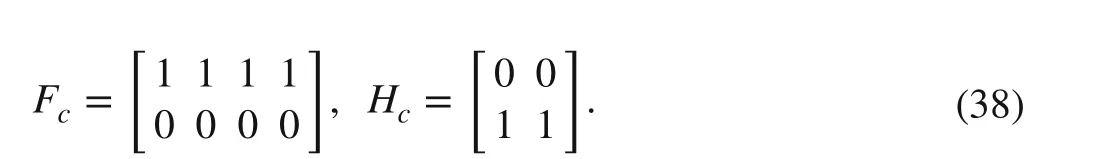
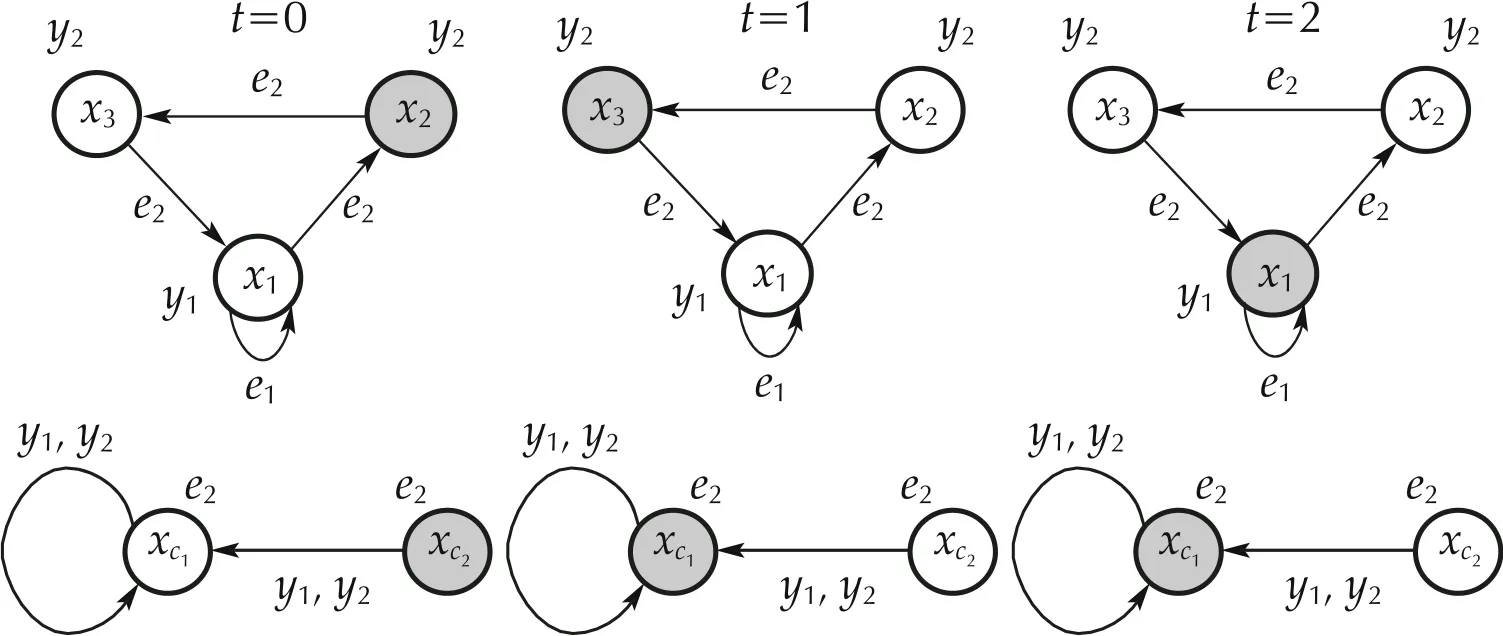
Fig. 9 DFA’s run for DFA in Example 1 considering x(0)=δ32 and xc(0)=δ22 and applying DFA controller ( 36)

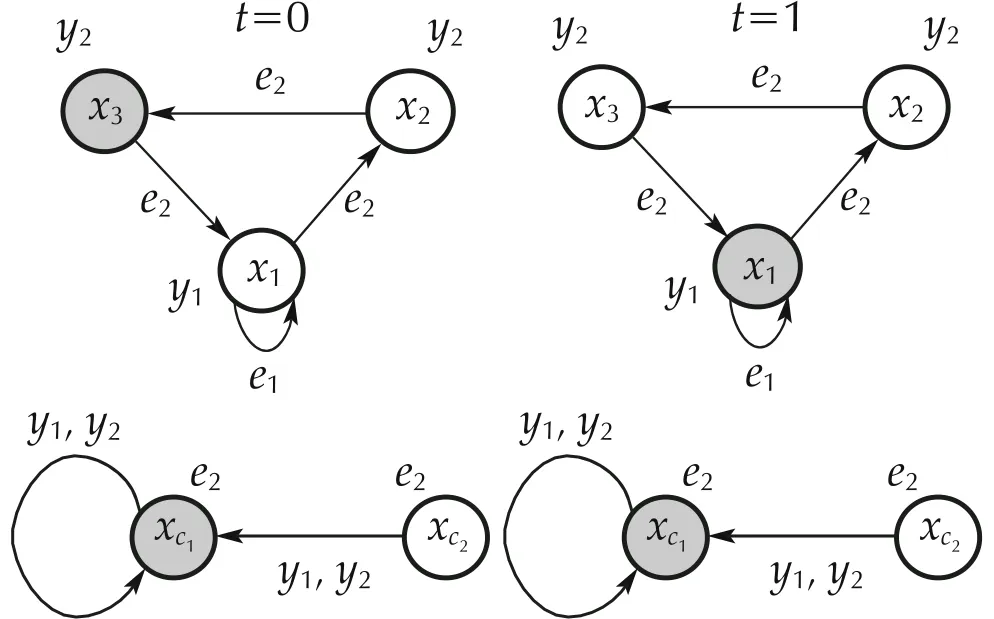
Fig. 10 DFA’s run for DFA in Example 1 considering x(0)=δ33 and xc(0)=δ12 and applying DFA controller ( 36)

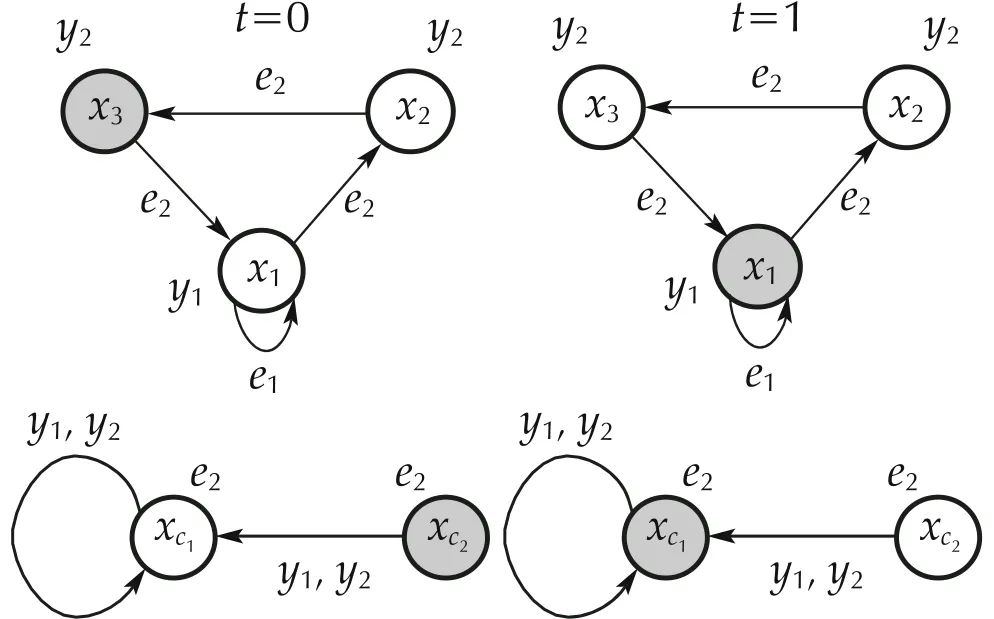
Fig. 11DFA’s run forDFAinExample 1considering x(0)=δ33 and xc(0)=δ22and applying DFA controller ( 36)

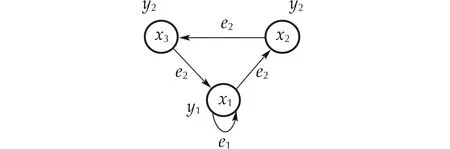
Fig. 12 DFA in Example 2

Example 3This example compares the feasibility of the static and dynamic stabilization problems of DFAs. One hundred DFAs with diff erent dimensions are randomly generated for this purpose. Two groups of random DFAs are generated which consist of DFAs with three and f ive internal states. In fact, f ifty DFAs have three and thither f ifty DFAs have f ive states.

The static and dynamic stabilization problems are independently applied to each generated DFA. Then, the number of feasible DFAs is obtained which are presented in Table 2.

Table 2 demonstrates two critical points. First, the number of DFAs which are static stabilizable is less than the dynamic stabilizable ones. It clearly exposes that the dynamic stabilization problems is less restricted than the static one. Second, the number of feasible numbers will reduce by the increment of the DFA’s states. Indeed, the feasibility of the static stabilization problem critically depends on the number of DFA’s states in comparison to the dynamic stabilization problem.

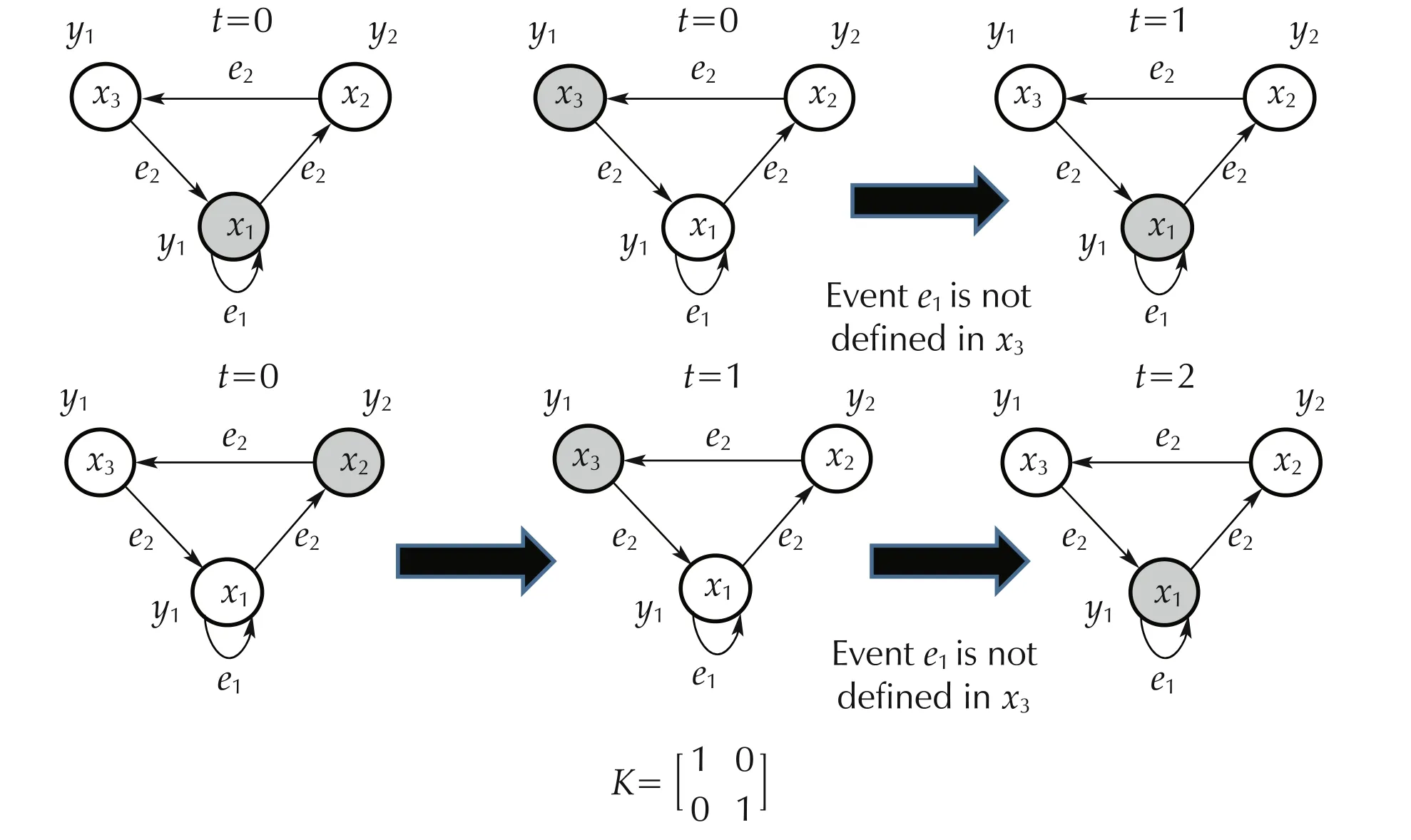
Fig. 13 DFA’s runs for the DFA in Example 2 for initial states by applying SOF controller in which K=

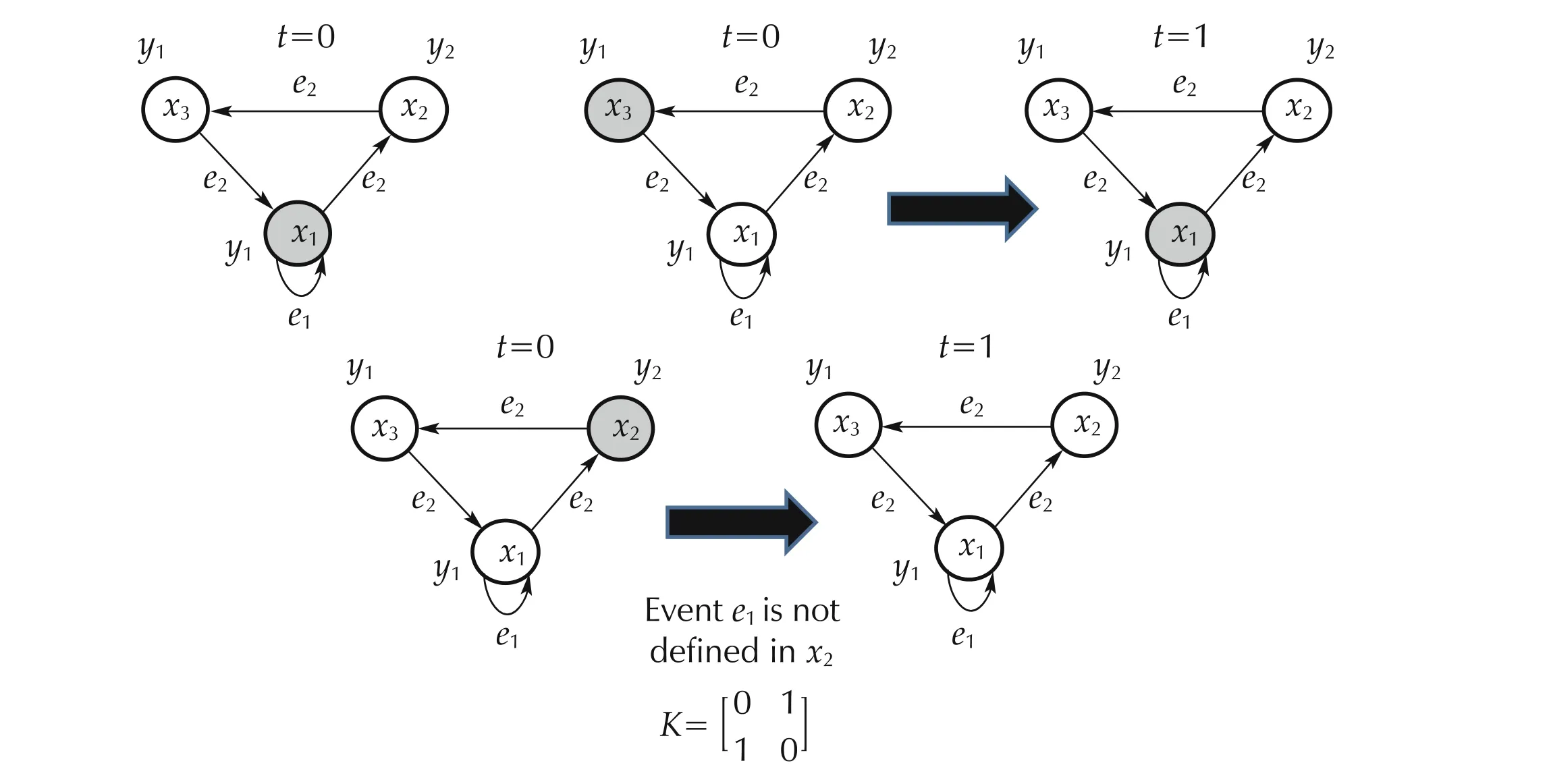
Fig. 14 DFA’s runs for the DFA in Example 2 for initial states by applying SOF controller in which K

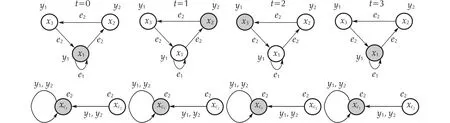
Fig. 15 DFA’s run for DFA in Example 2 considering x(0)=δ31 and xc(0)=δ21 and applying DFA controller ( 38)

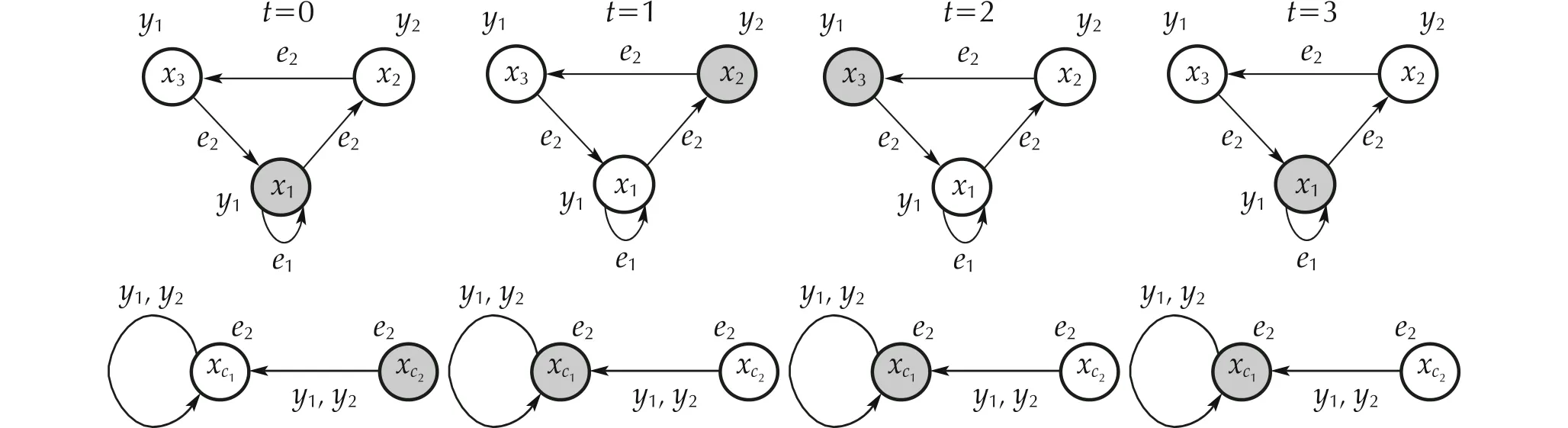
Fig. 16 DFA’s run for DFA in Example 2 considering x(0)=δ31 and xc(0)=δ22 and applying DFA controller ( 38)

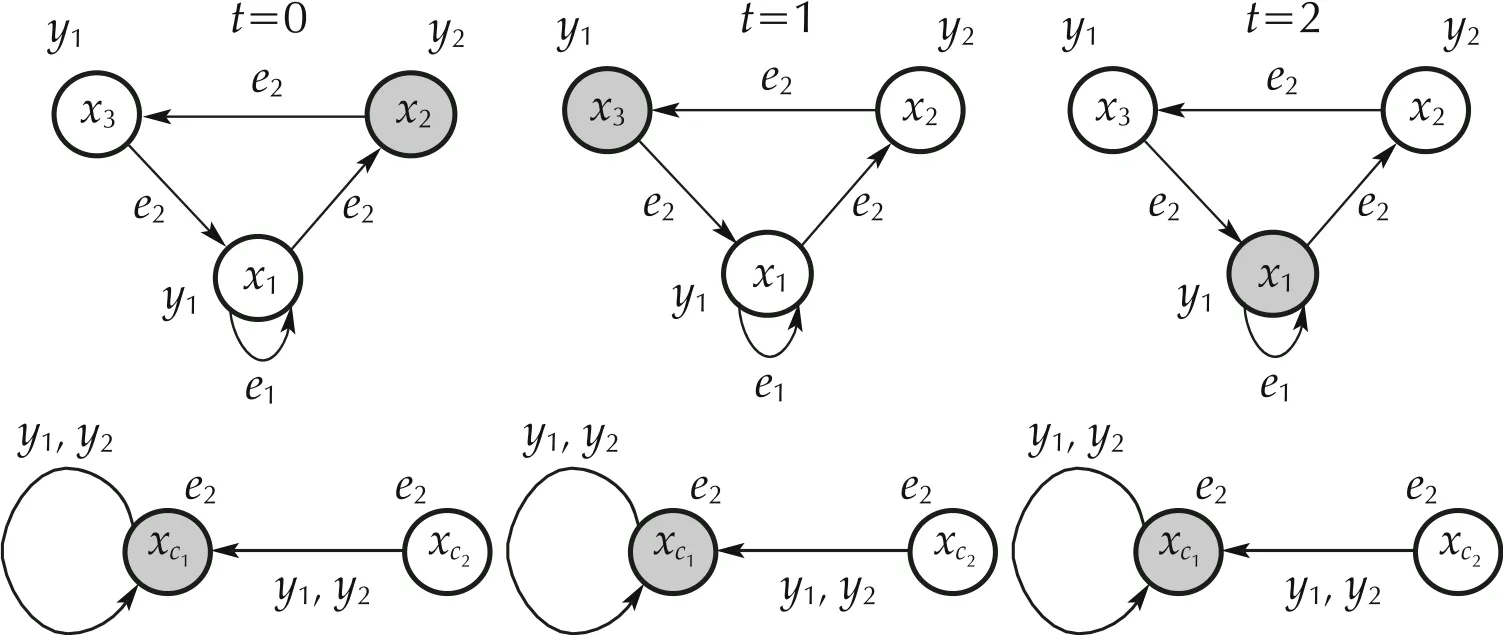
Fig. 17 DFA’s run for DFA in Example 2 considering x(0)=δ32 and xc(0)=δ21 and applying DFA controller ( 38)

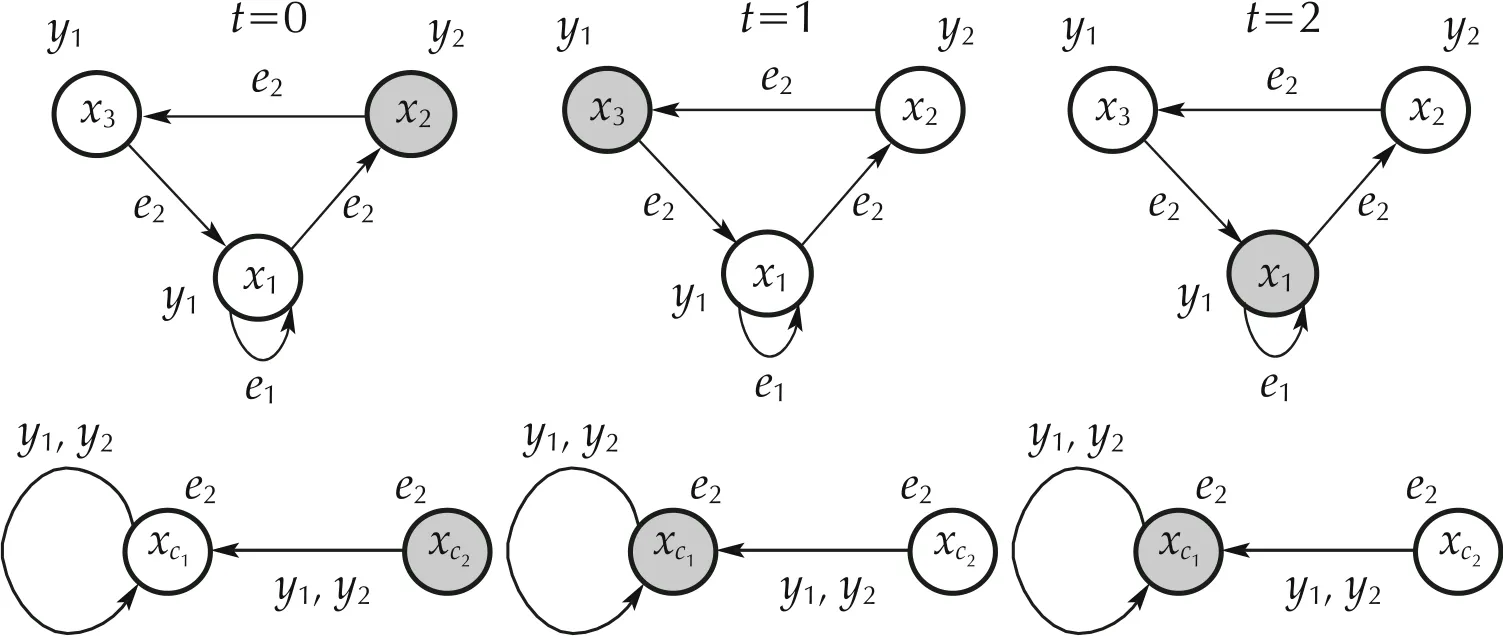
Fig. 18 DFA’s run for DFA in Example 2 considering x(0)=δ32 and xc(0)=δ22 and applying DFA controller ( 38)

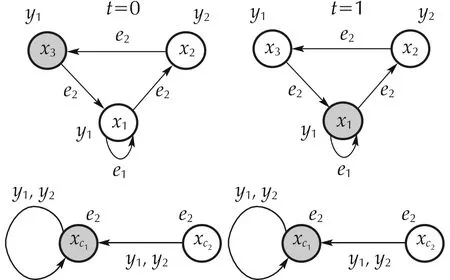
Fig. 19 DFA’s run for DFA in Example 2 considering x(0)=δ33 and xc(0)=δ12 and applying DFA controller ( 38)

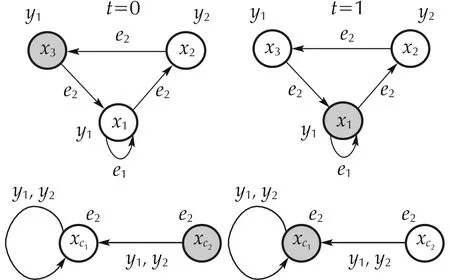
Fig. 20 DFA’s run for DFA in Example 2 considering x(0)=δ33 and xc(0)=δ22 and applying DFA controller ( 38)

Table 2 Number of feasible problems

5 Conclusions

This paper mainly focuses on the DOF stabilization of DFAs.For the f irst time, this paper suggests the DOF stabilization concept for DFA via considering another DFA controller. A design algorithm is proposed to design the DFA controller through generating all possible DFAs and investigating their ability to stabilize the equilibrium state. It has been shown that the DOF stabilization problem is less conservative than the SOF one. Furthermore, three simulation examples are provided to explain the aspects of the proposed controller.The examples show the superiority of the DOF controllers to stabilize the DFA in comparison to the SOF controllers.Finally, it is worth mentioning that the proposed idea can be easily extended to the nondeterministic f inite automata and logical networks (Boolean networks), as well. It is mainly because the dynamics of these systems can be rewritten as those considered in this paper. These facts can be investigated by future works in more details.