基于三阶测试诊断高中生曲线运动中的迷思概念

朱顺明 李文娟

（江苏省天一中学，江苏 无锡 214101）

1 问题的提出

曲线运动是自然界中更为常见的一种运动.在新人教版高中物理必修1中学生首先学习了直线运动，对运动学有了初步了解；学完牛顿运动定律之后，学生对力与运动的关系又有了进一步理解.在新人教版必修2《抛体运动》《圆周运动》《万有引力与航天》中，我们研究的视野由一维的直线运动拓宽到二维的平面坐标系中，将研究直线运动的方法和策略迁移到曲线运动中来.在讨论描述曲线运动的基本物理量（如位移、速度、加速度等）时，我们仍需要直线运动中相关概念进行分析.所以在曲线运动情境下的问题探讨是学生对运动学和动力学知识进一步拓展和延伸.由于人们习惯于研究直线运动，而对曲线运动规律的理解和运用更容易形成迷思概念.

“迷思概念”是我国台湾学者对英文“misconception”一词的有趣译法，其中“mis-”是音译部分，“conception”是意译部分，它是指学习者头脑中已形成的认识与科学概念不一致或相违背的概念.迷思概念的存在会影响学生对新知识的正确理解，具有普遍性、隐蔽性、顽固性和反复性，因此对迷思概念的诊断是教学研究中最重要的任务之一.

2 研究设计

2.1 研究对象

笔者在江苏省天一中学高二理科班物生地组合中随机抽取2个班级共104名学生进行测试.在学生已顺利通过2020年1月份江苏省合格性考试后，由教师亲自到班级发放测试题，采取无记名方式，答题时间规定为25 min.测试前事先告知学生本次问卷仅诊断与曲线运动有关的知识理解情况，与个人成绩和未来升学无关，这样确保学生认真答题，理性给出确定度.

本次研究共发放104份，回收94份，回收率90.4%.在录入数据时，将空白测试卷、未完全答题、没有给出确定度或确定度填写全部相同均视为无效卷.在回收的94份问卷中发现有效样本是78份，有效率82.9%.

2.2 研究方法

本研究采用三阶诊断测试和半结构化访谈来探查学生的迷思概念.

三阶诊断测试工具是参照Kaltakci，Derya&Didis，Nilufer等人研究方法，［1］将学生的诊断结果分为“知识缺失”、“迷思概念”、“行为疏忽”、“正确概念”4种（如表1所示）.其中第三阶若不确定，不管答案阶和理由阶是否正确均视为知识缺失.笔者认为存在知识缺失与迷思概念是有很大不同的，毕竟学习新知识与转变概念知识所采取的教学策略是有本质区分的.

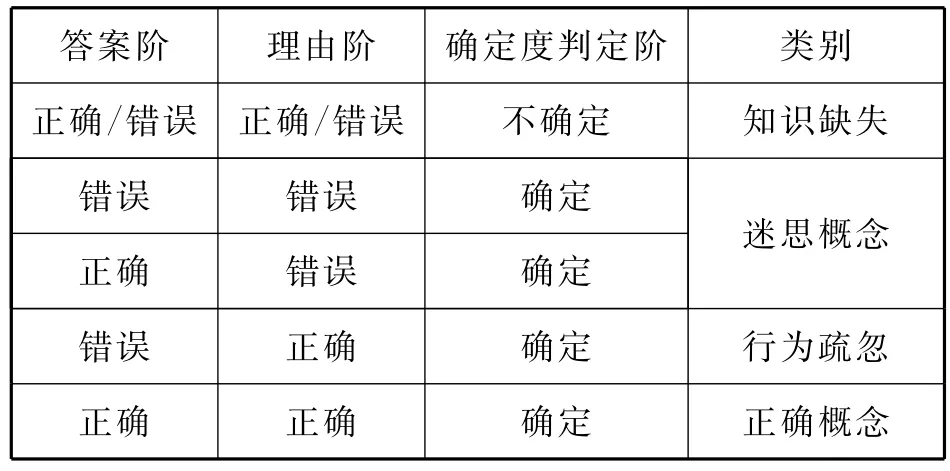
表1 迷思概念判定标准表

2.3 测试工具的编制

本测试题由三阶构成，第一阶（答案阶）考查学生对学科知识的理解情况；第二阶（理由阶）要求学生选择相应的理由，以评估学生对答案解释的合理性；第三阶（确定度判定阶）要求学生对答案阶和理由阶的整体确定性程度做出评价.目的在于辨析学生选出正确答案是猜测还是真正理解.为了更全面诊断测试，笔者研读有关曲线运动的迷思概念文献，分析教材内容，立足课堂教学实践，并与教学同仁和教研员不断探讨交流，最终编制出12道测试题.对编制好的题目先试测，针对测试结果与学生开展半结构化访谈，以深入了解学生存在迷思概念根源，完善试题表述，保证试题的可读性和针对性，最后重新修订得到较为成熟的三阶测试题.对测试数据运用SPSS软件进行计算统计，其克伦巴赫信度系数为0.789，具有较高的可信度.

2.4 测试内容分布

围绕曲线运动相关内容，本人设计的三阶测试题涉及3个知识点：运动合成与分解（分运动与合运动、平抛运动时间）；圆周运动（最高点速度、向心力）、卫星模型（运行速度、发射速度、拉格朗日点、变轨运行），共12道题目.对应的题号如表2所示.

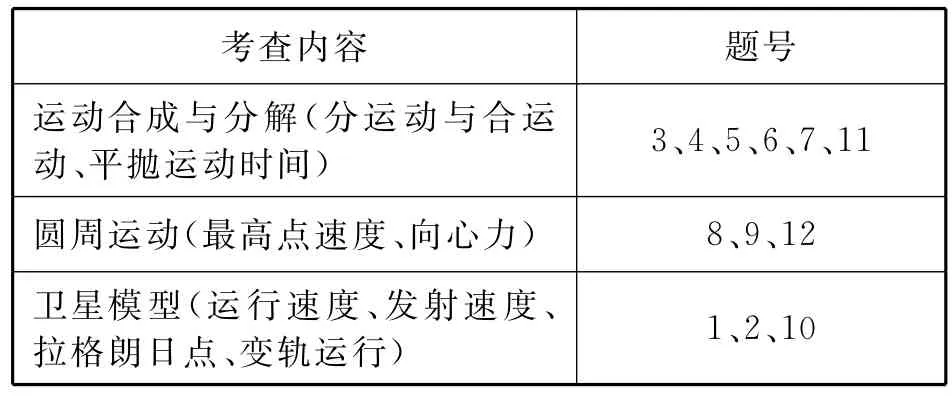
表2 考查知识点与对应题号列表

3 测试结果分析

3.1 一阶和二阶正确率对比

一阶和二阶正确率统计：一阶得分只看答案阶，正确计为1分，错误不计分；二阶得分要求答案阶和理由阶都正确才计为1分，若有任何一阶错误就不计分.［2］

如图1所示，12道测试题中第1、8、12题一阶正确率与二阶正确率相同，可见学生选择正确的答案与相应的理由匹配度较高.其他题目一阶正确率均高于二阶正确率，说明学生选择出正确答案，但并没有给出正确的理由.可见有些学生仅凭感觉答题但实际并没有真正掌握.显然单凭一阶的答题情况是无法诊断出学生的实际水平，有时难免出现高估学生的学习能力的现象.因此加入理由阶和确定度判定阶进行诊断迷思概念是十分有必要的.

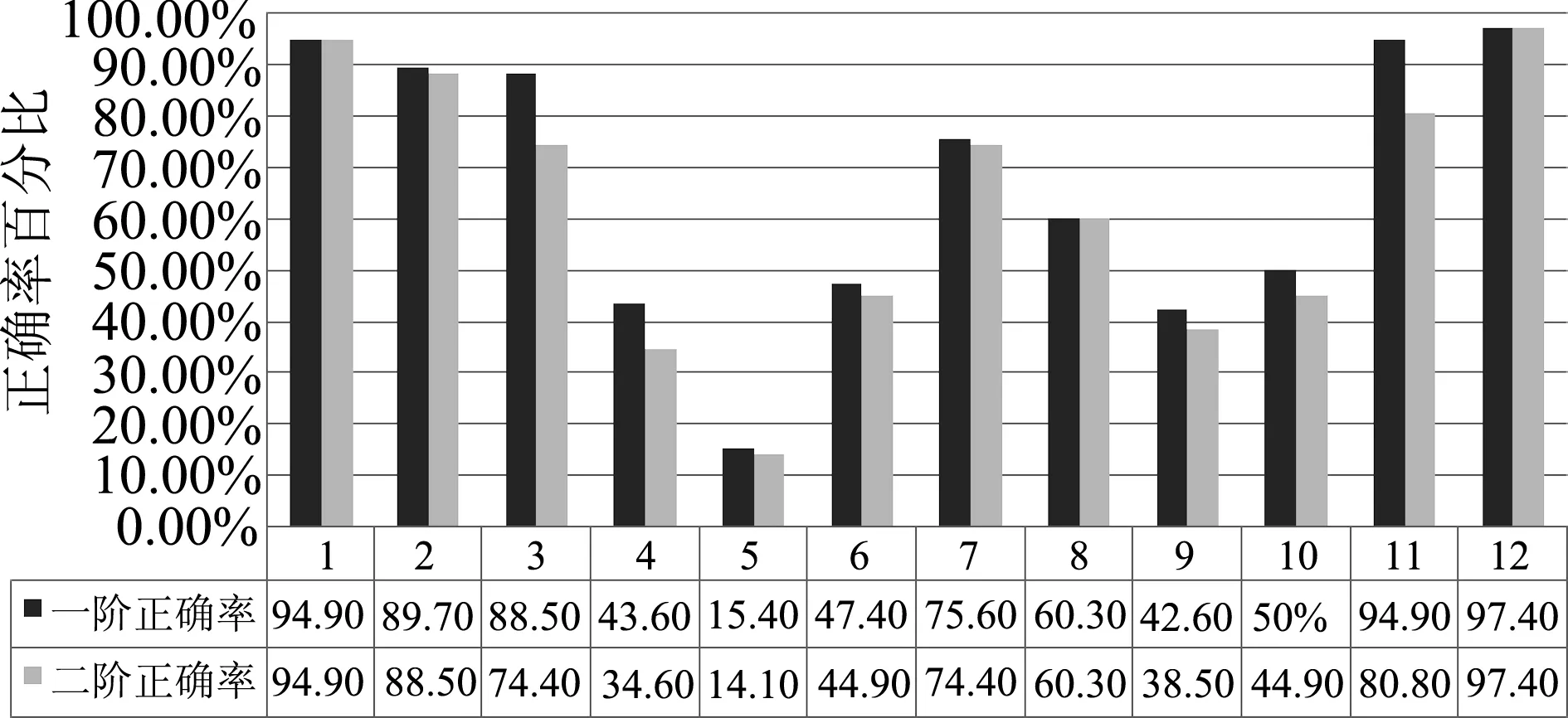
图1 一阶和二阶正确率表格数据

3.2 三阶测试结果分析

通过对问卷试题的分析，表3中列出了此次测试诊断出的11个迷思概念.其中有6个迷思概念学生表现突出，人数比例超过20%.

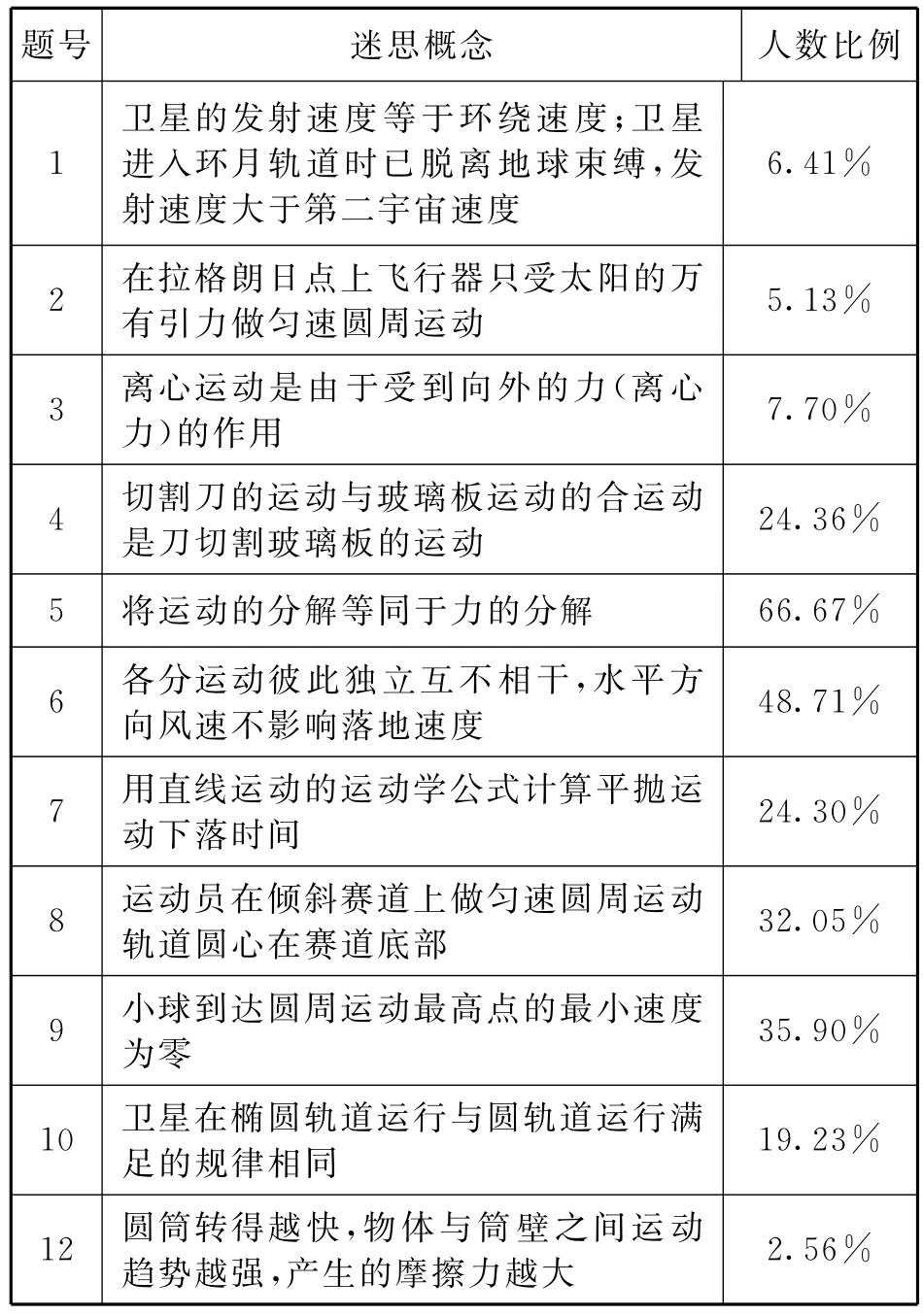
表3 与曲线运动相关知识迷思概念情况

从表3中可以看出，学生在运动的合成与分解和圆周运动概念认识上严重不足，应引起教师足够的重视，在卫星模型方面表现较好.具体分析如下：

3.2.1 运动的合成与分解迷思概念

（1）错误类比型：即学生将新知识与以往学过的旧知识间建立错误的类比迁移.24.36%的学生把刀切割玻璃问题与小船渡河相类比，认为只要保证刀对地的速度与玻璃对地的速度的合速度垂直于玻璃板即可.实际上刀垂直切割玻璃板的运动仅仅是割刀的一个分运动v刀板，另一个分运动是与玻璃板相对静止一起向右v板地，它们的合运动v刀地才是相对地面的运动.66.67%的学生将运动的分解等同于力的分解，将拉绳速度在水平方向进行分解得到船靠岸的速度.如图2所示，一人拖着旅行箱在地面上行走，根据力的效果将拉力进行分解.一般将力F向水平方向（使物体向前的力F1）和竖直方向（使物体离开地面的效果的力F2）分解.而此题小船并没有竖直向上运动的效果，所以速度分解与力的分解有所不同.

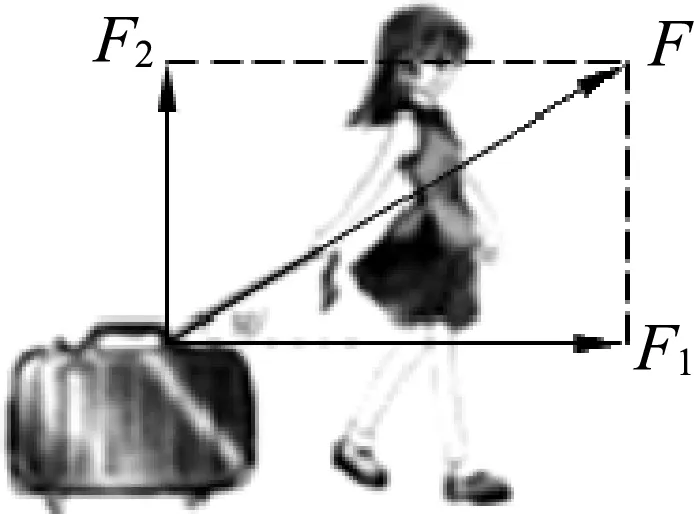
图2 人拖着旅行箱行走

（2）情境错配型：即在相同的知识概念下因所处情境变化导致出错.48.71%的学生认为水平风速不影响落地速度.这是因为在新授课中教师常常以蜡块在玻璃管中运动为例强调各分运动独立性，并且平常遇到的问题情境也都是水平风速不影响下落的时间.而现在是问降落伞落地速度变化，这时学生不能仔细甄别情境的变化，凭借对日常所做题目和配图的记忆而导致出错.

（3）思维固化型：即运用规律和方法在解决实际问题时所表现出心理活动的倾向性.它是学生对物理模型的机械记忆而产生固化的思维路线、定型化的程序模式和同一的方法套路.24.30%的学生在分析平抛运动下落时间依然直接用直线运动的运动学公式来处理.

3.2.2 圆周运动迷思概念

（1）生活经验型：生活是物理之源，观察是物理之眼.但有些看似合理的现象因缺乏科学分析而产生错误的认知.7.70%的学生认为物体在拐弯时存在向外的离心力，这与生活体验有关.比如骑自行车拐弯时人会有向外甩出去的趋势，此时人就感觉有向外的作用力，对此在进行受力分析时学生会添加向外的离心力.而实际上离心运动不是受到离心力的作用，而是向心力不足.

图3 场地自行车比赛

（3）主观臆想型：即用某一物理规律片面解释物理现象从而得到错误结论.35.90%的学生认为圆周运动最高点的最小速度为0.学生根据经验竖直上抛一个物体其速度减为0时表明物体已到达了最高点.所以主观认为小球运动到最高点的最小速度为0，接下来小球将只受重力作用做自由落体运动.但事实上做圆周运动的小球最高点的临界速度（最小速度）是（最高点绳对小球的拉力刚好为0，只有重力提供向心力）.2.56%的学生认为圆筒转得越快，物体与筒壁之间运动趋势越强，与筒壁挤压越紧弹力越大，故产生的摩擦力越大

3.2.3 卫星模型迷思概念

（1）思维固化型：即学生习惯性按照以往的思维方式思考问题，而不遵循客观事实分析.5.13%的学生认为飞行器运行规律依然遵循卫星围绕行星运动模型.而此情景中飞行器位于拉格朗日点轨道，在这个点飞行器几乎不需要消耗燃料实现与地球同轴转动.此时飞行器同时受到太阳和地球引力的共同作用，不同于常规卫星模型.

（2）模型偏差型：即受教材知识和学生能力限制，教学中需要从实际情景抽象出理想模型进行研究.这使得学生对概念的内涵和外延缺少严谨性，在使用规律时往往会产生模型混乱.19.23%的学生认为卫星在变轨运行中椭圆轨道与圆轨道遵循相同的动力学规律.新人教版必修2教材上有这样的一句话，行星的椭圆轨道与圆十分接近，在中学阶段我们一般按圆轨道来处理.并且在高中有关椭圆的曲率半径问题也没有过多涉及，这就导致学生把椭圆运动都近似为圆周运动处理.

（3）概念不清型：6.41%的学生认为当卫星进入环月轨道时已脱离地球的束缚，所以其发射速度应大于第二宇宙速度，更有甚者把发射速度直接等同于运行速度.学生孤立的认为卫星绕月运行，只受到月球的万有引力，殊不知它们仍属于地月体系.

4 研究结论与建议

4.1 研究结论

通过高中生曲线运动的三阶测试题，不仅可以了解学生的答题思路，而且可以 更深入展现学生产生迷思概念的类型，以帮助学生构建科学的物理概念提供更为可靠的诊断结果.现得到的结论如下.

（1）学生产生迷思概念的类型分别包括错误类比型、情境错配型、思维固化型、生活经验型、概念不清型、主观臆想型、模型偏差型等7种.［3］

（2）不同类型对学生的影响差异性不同.通过对3个主题的迷思概念原因深度剖析，我们发现错误类比型、情境错配型表现最为突出.所以开展概念变式教学，比较教学是教学研究者关注的方向.

（3）由于三阶测试只有一项确定度判定阶，这就要求答案阶与理由阶具有相同的确定度，但实际上可能出现答案很确定但理由却不确定现象.这就要求在答案阶和理由阶后面分别加入确定度判定阶，即四阶测试题.这样我们可以诊断出更精准的迷思概念，以帮助教师更好地对症下药，进而采用更合适地转变策略.

4.2 教学建议

通常学生已有的知识和概念是影响他们解决问题以及进一步获取新知识的能力水平.

（1）关注和挖掘学生的迷思概念.迷思概念是教师进行概念教学的起点和重要的资源库，也是实现有效教学的重要突破口.

（2）探寻和研究学生的迷思概念类型.教师根据诊断结果对若干迷思概念进行分门别类，深入了解其特点，然后有针对性地采用恰当的教学策略促进学生的概念转变.

（3）丰富教学方式整合教学资源.在教学过程中教师要将新知识与学生已有的经验有机结合起来，加强教学资源的整合，［4］注重对比与探究，创设合理的教学情境，让学生经历概念的生成，领悟概念的本质.当学生对知识理解越透彻，思维启发越严密，由认知偏差带来的负面影响就越小.当教师对转变策略掌握越丰富，遇到问题时他采取的教学方式就越多样，对迷思概念的转化就越有针对性，学生的迷思概念水平就会降低.