softmax变区段非线性双拟合方法及其FPGA实现

肖望勇，张驾祥，徐界铭，谭会生

(湖南工业大学 交通工程学院，湖南 株洲 412007)

人工神经网络作为人工智能的关键技术，已经成为世界各国争相发展的战略技术之一，也是新一轮科技和产业变革的重要驱动力量.FPGA因为具有可重构、低功耗、易控制、高性能等优势[1-2]，所以非常适合被用于实现神经网络.近年来，其在深度学习领域的应用也越来越多，许多大型公司(如百度、微软、IBM等)都有专门的FPGA研发团队.在人工神经网络的实现过程中，需要对大量的非线性激活函数进行计算，因此在该领域内研究FPGA如何高速地处理非线性激活函数具有十分重要的意义.在机器学习领域，尤其是深度卷积神经网络学习中，softmax是一个常用并且非常重要的函数，它以概率形式来显示多种分类结果，在多分类应用场景被广泛使用.

FPGA因其可重构技术的灵活性，如今已成为解决复杂函数高速计算问题的强大工具.目前用FPGA计算复杂函数的常用方法有CORDIC算法[3]、查找表法[4]、泰勒级数展开法[5]、多项式拟合法[6]等.其中，CORDIC算法是一种通过多次迭代将复杂运算转换为仅需移位和加法运算的算法，其资源需求较少.但是，随着精度要求的提高，迭代次数增加，其运行速度就会降低.查找表法是将不同输入值对应的计算结果事先保存在ROM中，使用时直接从内存中提取结果，省去了复杂的运算，运算速度快并且容易实现，但随着精度要求的提高，查找表法也需耗费大量的存储资源.泰勒级数展开法，随其阶次的增加，会加大乘法和加法器的使用量，资源消耗非常大.多项式拟合非线性函数，随着拟合函数阶次的增大，会消耗大量的乘法器资源.神经网络对激活函数的拟合需要的阶次较多，计算1个函数值就需要许多乘法器，且消耗时间长.

为解决上述问题，本文采用分段非线性逼近法来处理softmax函数，即将softmax函数在一定范围内划分为几段，每段均用次数较低的多项式进行拟合.这种方法不仅可以保证计算精度，还可以减少计算的时间，较好地平衡了两者之间的矛盾，并且它还具有资源耗费少的优点，实现也比较方便.

1 softmax变区段非线性双拟合方法

假设有1个数组V，Vi是数组中第i个元素，则这个元素的softmax值是Si= ei/ ∑ ei.其中，Si表示Vi的softmax值，即第i个元素的指数与所有元素指数和的比值；分母 ∑ ei是所有元素指数的和，为固定值.显然，只需对其中的ei进行拟合即可.下面，对分子ei进行拟合分析.

文献[7]用传统分段非线性拟合函数ei得到了较高的精确度，但未给出具体的分段方式.为了进一步提高精度，可采用非均匀分区的非线性函数拟合ei，其拟合原理参见文献[8].函数的N+1阶导数的绝对值越大或越小，表示此函数在该点处使用N阶多项式进行逼近的误差也越大或越小，所以，该点对应分段区间的间隔应该取较小或较大的值.根据ei的N+1阶导数依然是ei的性质，说明使用N阶多项式进行逼近的误差随i的增大而增大，所以，分段区间的间隔应该随i的增大而减小.由于ei函数值会随i的增大呈指数上升，拟合函数右端区间的误差相对于其他区间会偏大.针对这一问题，通过均匀分段和多次随机分段发现，若函数ei在区间(−8, 8)上以整数6为分界线，则大于分界线的区间误差比小于分界线的区间误差要大得多.因此，对大于分界线的区间，即(6, 8)，将其区间间隔设置为＜1；而对小于分界线的区间，即(−8, 6)，将其区间间隔设置为＞1.对其他函数的拟合思路也是如此，即先通过均匀分段和多次随机分段找出误差大的集中范围，再针对该范围给予相对较小的区间间隔，从而得到更高的精度.

2 softmax变区段非线性双拟合的python仿真

python具有简单易学、运行速度快、易于维护等优点，还具有丰富的函数库，其功能十分强大，是现在计算机程序设计的主流语言之一，非常适用于人工智能领域.因此，本研究选用python语言来完成函数的拟合，开发软件选用jupyter notebook.函数拟合的具体步骤如下：先调用numpy库中的polyfit函数进行拟合，再调用matplotlib库进行图像的绘制.在拟合过程中应综合考虑计算速度和所需资源，将函数ei在区间(−8, 8)分为9个子区间进行拟合，根据前文所提的高精度二次非线性拟合方法，设置好分段区间间隔.python拟合的具体流程如图1所示，拟合的函数曲线如图2所示.从图2可以看出，拟合函数曲线与指数函数曲线几乎重合，这说明函数的拟合效果良好.

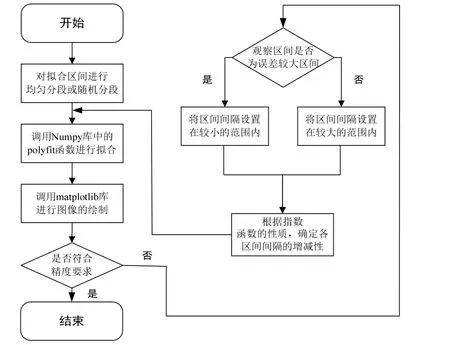
图1 非线性双拟合的python拟合流程

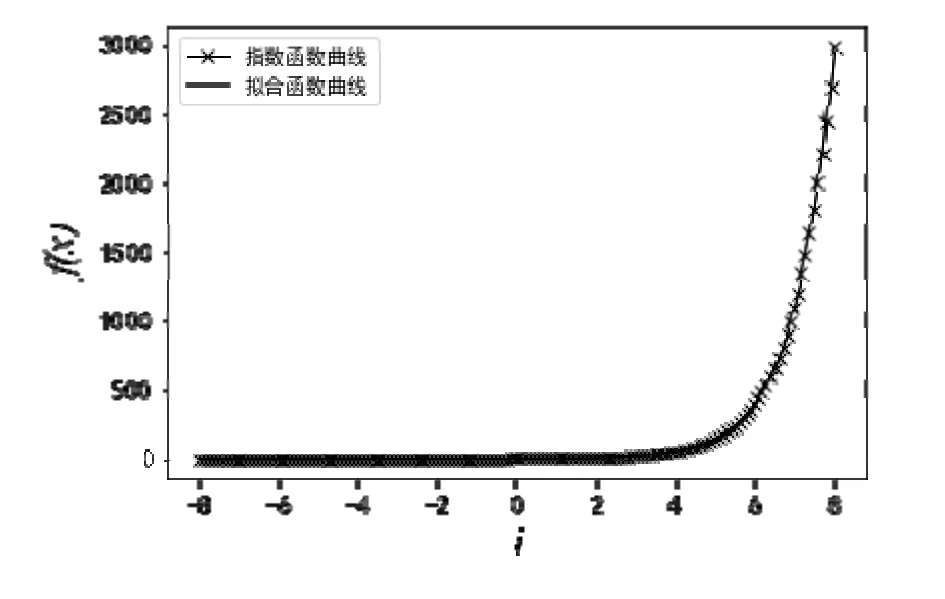
图2 非线性双拟合的python拟合函数曲线

各分段区间的拟合函数如表1所示.在区间(−8, 8)随机取10个输入数据，取点精度为0.01，所得拟合函数值的误差如表2所示.

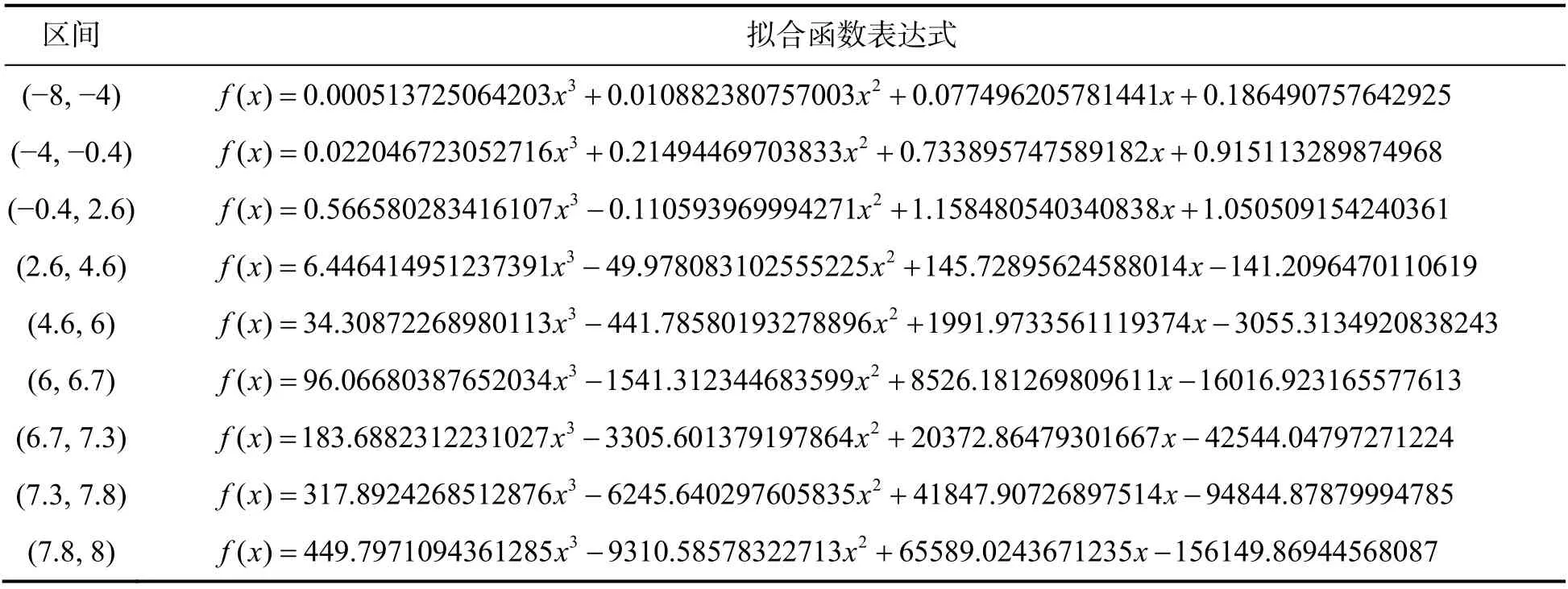
表1 python分段拟合softmax函数

由表2可看出，softmax函数随机点用python拟合的绝对误差均＜0.01，相对误差也基本＜0.4%；靠近图像右端区间的点的绝对误差只有0.001，相对误差＜0.01%.这说明拟合函数的右端区间误差相对其他区间偏大的问题得到了解决，其整体精度也较高，即利用python语言和改进的分段方式，对softmax函数的拟合效果良好.

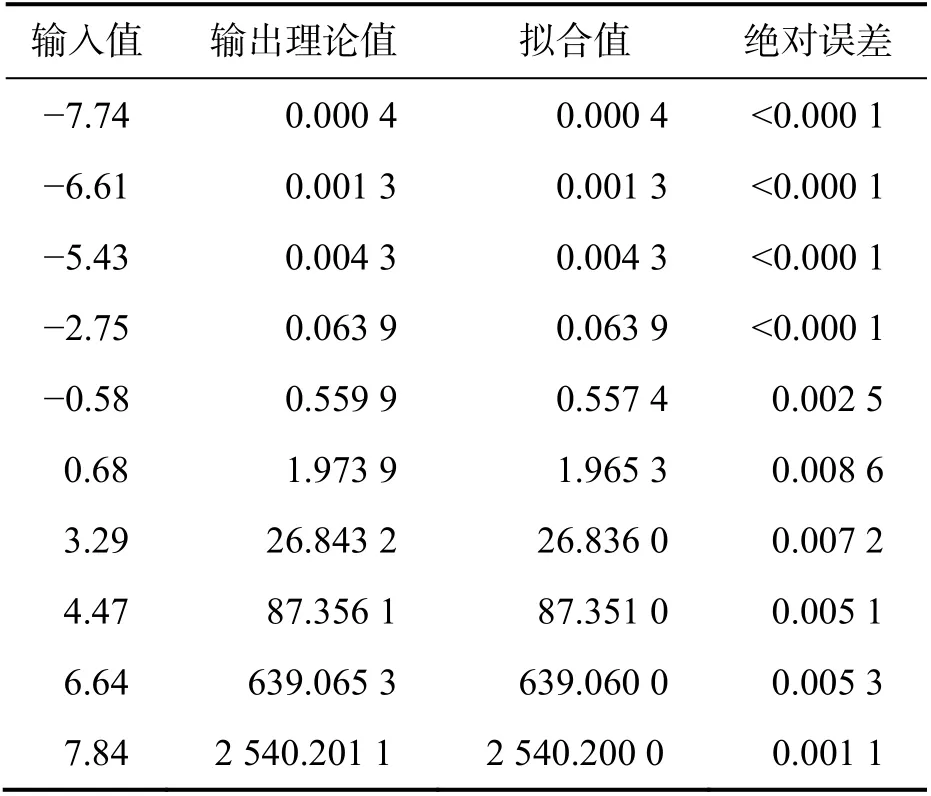
表2 softmax函数随机点的python拟合结果

3 softmax变区段非线性双拟合的FPGA实现

实验使用美国XILINX公司的XC7A35T-1CPG236C FPGA平台来实现函数拟合.从表1可知，python拟合的softmax函数是由加法和乘法组成的多项式，所以FPGA实现的硬件电路会用到乘法器和加法器，可使用Vivado软件在其Block Design中调用IP核来实现拟合函数的硬件电路，指数函数的拟合表达式为

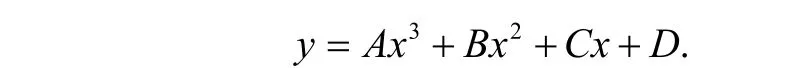
FPGA实现的结构如图3所示.

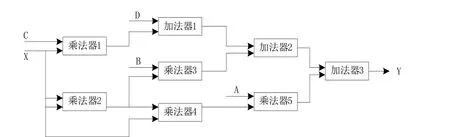
图3 非线性双拟合函数的FPGA实现

在FPGA中实现浮点数的乘法运算有2种方法，即定点小数运算和浮点运算.定点小数运算虽然方便，但由于运算过程会舍弃一些位数，降低了运算精确度，所以这里采用浮点运算专用IP核Floating-point.此IP核在浮点运算方面的性能非常好，符合IEEE-754标准，并且它使用的是AXI4-Stream总线协议，其高效、易用的特点适合在神经网络中使用.

拟合函数表达式y=Ax3+Bx2+Cx+D的具体实现过程如下：首先，创建Block Design文件，并在其中添加IP核Floating-point；其次，对IP核进行设置(可设置为加法器或乘法器)，并设定为双精度的浮点数运算；然后，绘制好电路，添加端口和连线，完成后检查程序框图是否有误；最后，点击Create HDL Wrapper，添加Testbench代码，即可开始仿真测试.分段区间的FPGA拟合函数如表3所示，FPGA仿真结果如图4所示.

表3 FPGA分段拟合softmax函数

图4 softmax函数的FPGA仿真结果

随机在区间(−8, 8)取10个数，利用FPGA硬件电路进行计算，其拟合结果如表4所示.其中，当x=7.90时，浮点数IP核所使用的是IEEE-754标准数，所得结果y为40A512900EC489C0，转换为浮点数约等于2 697.281 362 668 814 8，而当i=7.90时，ei=2 697.282 328 268 510，两者绝对误差约为0.001.

表4 softmax函数随机点的FPGA拟合结果

从表4可以看出，softmax函数随机点FPGA拟合结果的绝对误差均＜0.015，相对误差基本＜1.2%；拟合函数曲线右端区间的点的绝对误差约为0.001，相对误差＜0.01%.这说明FPGA对softmax函数的整体拟合效果良好，精度较高，并且有效地解决了ei拟合函数的右边区间点误差偏大的问题.通过仿真测试还发现，softmax函数的拟合运算时间在纳秒级，单次运算的平均时间在3.75 ns左右.

为进一步验证本文所提拟合方法的性能，将该方法与文献[7]的分段函数拟合方法在同样的平台下进行实验对比，具体结果如表5所示。

表5 不同方法的FPGA拟合性能对比

由表5可以看出，采用本文变区段非线性双拟合方法和文献[7]所提的分段非线性拟合方法来实现softmax函数，其精度与计算速度均有了较大的提升。

4 结语

本文针对人工神经网络常用的softmax函数，基于其指数函数的特性，提出了一种变区段非线性双拟合方法.首先，通过均匀分段和随机分段找出误差较大或较小的区间，对不同误差的区间进行不同间隔的分段，即变区段二次非线性拟合；其次，运用python进行softmax函数的拟合逼近实验，并最终在FPGA上得以实现.所提方法解决了使用分段非线性拟合法在某些区间点误差较大的问题，且在保持较高拟合精度的同时，利用FPGA来实现还使得系统具有良好的实时性.