非监督武术竞赛场地分割算法

孙瑞阳 孙玉滨 段炼 赵蓝飞

【摘要】    本文提出一种非监督武术竞赛场地分割算法。首先通过高斯混合模型，对武术竞赛场地进行建模;其次通过期望最大算法对高斯混合模型的参数进行最优估计并得到多个候选阈值;最后通过凸包算法对候选阈值进行筛选并最终确定武术竞赛区域。实验结果验证本文算法可以较为准确的分割武术竞赛场地。

【关键词】    武术竞赛场地分割    高斯混合模型    期望最大    凸包

Abstract：  This paper proposes an unsupervised Wushu competition field segmentation algorithm. Firstly， Gaussian mixture model is employed to modeling Wushu competition filed. Secondly， the parameters of Gaussian mixture model are optimally estimated and several candidate thresholds are obtained by expectation maximum algorithm. Finally， those candidate thresholds are filtered and the Wushu competition is segmented by convex hull algorithm. Experimental results demonstrated that the proposed algorithm has an accurate effect on Wushu competition field segmentation.

Keywords：  Wushu competition field segm

引言

近年来随着数字图像处理技术的不断进步，体育竞赛中融入了很多智能图像处理技术，例如运动员姿态估计，运动员目标检测与跟踪，运动员姿态识别以及运动员动作自动评分[1～3]。由于竞赛场地分割有助于提升运动目标检测、姿态识别、动作评分的准确度，因此这一技术成为近年来学术界研究的热点问题。

典型的竞赛场地分割算法包括：殷伟良等[4]提出的基于Hough直线检测和最小二乘拟合的自动场地检测算法。张龙飞等[5]提出的基于Canny算子和数学形态学方法的竞赛场地分割算法。Hung等[6]提出的基于颜色特征的广义竞赛场地分割算法。Homayounfar等[7]提出的基于深度结构模型的体育场地定位算法。

尽管这些算法能够分割出竞赛区域，但是场地分割结果存在漏分割或错分割等现象，另外到目前为止仍然没有一个针对武术竞赛场地分割算法。为了准确对武术竞赛区域进行分割，本文提出一种非监督武术竞赛场地分割算法。该算法根据武术竞赛场地的特点利用顏色作为数字特征，通过高斯混合模型[8]（Gaussian Mixture Model， GMM）对武术竞赛图像进行建模。

通过期望最大（Expectation Maximization， EM）算法[9]对GMM模型的未知参数进行非监督式最优估计。通过基于Jarvis步进法的凸包最优算法[10]对武术竞赛区域进行最优分割。实验结果验证本文算法可以有效地分割武术竞赛区域，准确率，召回率，交并比均高于同类算法。

一、本文算法

1.1  基于GMM模型的建模算法

假设R，G，B分别表示图像的红、绿、蓝三通道的灰度数组，由于武术竞赛场地主要由蓝色色调构成，因此为了分割武术竞赛场地本文采用如式（1）所示的色调特征用于区分某一像素是否属于竞赛场地区域。

其中i， j分别表示该像素的横、纵坐标，x表示色调特征随机变量X的一组观测值。令随机变量X的概率密度函数由K个含有未知参数的高斯函数进行加权，则X的概率密度函数如式（2）所示：

式中是未知高斯函数的参数集，μ、σ分别对应高斯函数的均值和标准差，隐变量表示样本xi， j来自哪一个高斯分布，α代表高斯模型的权重。

1.2  基于EM算法的参数估计算法

未知参数集θ的最大似然估计如式（3）所示：

1）随机选择迭代参数初始值θ（0）;

2）令第l次迭代对应的未知参数集θ值为θ（l），计算后验概率分布Q（l），令表示高斯分布概率密度函数，则Q（l）的计算方法如式（5）所示：

3）计算第l+1次迭代θ的初值为θ（l+1），其计算方法如式（6）所示：

4）重复步骤2）和步骤3）直到迭代收敛，此时得到对于未知参数的最优估计。

1.3  确定候选阈值

假设通过GMM模型和EM算法将特征值概率密度拟合为K个高斯分布，由于每两个高斯分布之间必存在一个交点，因此K个高斯分布存在个交点。令这些交点对应的特征值可以表示为。

由于每个交点代表不同的图像区域出现的概率转换点，因此本文选用这些特征值的交点作为分割武术竞赛区域的候选阈值，即对于第k个候选阈值来说，样本xi， j属于竞赛区域的条件是xi， j≥tk。

1.4  基于凸包算法的区域分割算法

由于存在多个阈值候选点，每个阈值候选点都有其对应的分割区域。即使采用最优的阈值进行图像分割，也会产生过分割或者漏分割像素点。因此本文采用基于Jarvis步进法的凸包最优算法用于筛选候选点并准确地分割武术场地区域。

二、 实验结果与分析

本文通过Matlab2016a对算法进行仿真验证。实验采用的硬件平台处理器是i5-10210U，内存16G，显卡MX250。实验部分对比Hung算法，Homayounfar算法以及本文算法。各算法对于场景一的分割结果如图1所示。

由图1可知Hung算法的错分割现象比较严重，除武术竞赛场地区域外，Hung算法将与竞赛场地区域亮度、色彩相近的区域也划归竞赛场地区域;虽然Homayounfar算法能够改善错分割现象，但是该算法在竞赛区域边界的分割效果不理想，部分非边界像素被划入到竞赛区域;通过本文算法分割出的区域与真实的武术竞赛区域重合度非常高，因此本文算法的精度高于前两种算法。

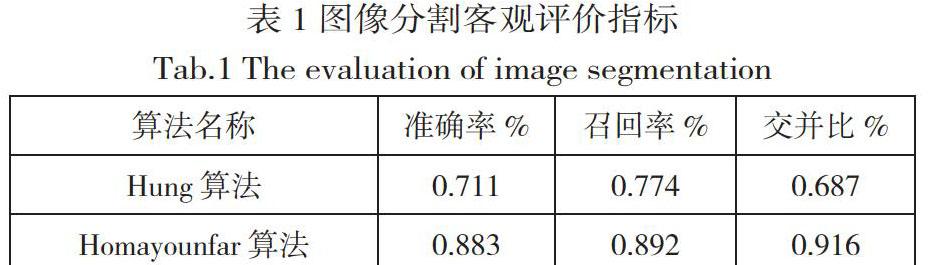
表1对比了两个场景下竞赛场地分割结果对应的准确率、召回率、交并比[12]。

由表1可以各算法的客观评价指标与如图2所示的图像分割效果基本保持一致。因此本文算法可以有效地分割武术竞赛场地区域，且分割的精确度较高。

三、结论

本文提出一种非监督武术竞赛场地分割算法，该算法通过GMM模型对武术竞赛区域进行建模，通过EM算法对GMM模型的未知参数进行最优估计，通过基于Jarvis步进法的凸包最优算法对候选阈值以及凸包区域进行筛选，进而筛选出最优的武术竞赛区域。实验结果表明本文算法能够有效地分割武术竞赛区域。

参  考  文  献

[1] Zhang F， Zhu X， Ye M. Fast human pose estimation[C]//Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 2019： 3517-3526.

[2] Buri? M， Pobar M， Iva?i?-Kos M. Object detection in sports videos[C]//2018 41st International Convention on Information and Communication Technology， Electronics and Microelectronics， 2018： 1034-1039.

[3] Merler M， Mac K N C， Joshi D， et al. Automatic curation of sports highlights using multimodal excitement features[J]. IEEE Transactions on Multimedia， 2018， 21（5）： 1147-1160.

[4]殷伟良， 陈临强， 李伟. 体育视频中场地自动检测方法[J]. 计算机系统应用， 2012， 21（5）： 184-188.

[5]张龙飞， 曹元大， 张明杰， 等.体育视频中的对象检测与分割[J]. 計算机工程， 2006（03）： 229-230+239

[6] Hung M H， Hsieh C H， Kuo C M， et al. Generalized playfield segmentation of sport videos using color features[J]. Pattern Recognition Letters， 2011， 32（7）： 987-1000.

[7] Homayounfar N， Fidler S， Urtasun R. Sports field localization via deep structured models[J]. 2017 IEEE Conference on Computer Vision and Pattern Recognition， 2017： 4012-4020.

[8] McLachlan G J， Rathnayake S. On the number of components in a Gaussian mixture model[J]. Wiley Interdisciplinary Reviews： Data Mining and Knowledge Discovery， 2014， 4（5）： 341-355.

[9] Do C B， Batzoglou S. What is the expectation maximization algorithm？[J]. Nature Biotechnology， 2008， 26（8）： 897-899.

[10]Wilderjans T F ， Ceulemans E ， Meers K . Multichull： A generic convex-hull-based model selection method[J]. Behavior Research Methods， 2017， 45（1）：1-15.

[11] Gonzalez R C， Woods R E. Digital image processing [M]. 3nd ed. Beijing： Publishing House of Electronics Industry， 2017： 497-502.

[12]Zaitoun N M， Aqel M J. Survey on image segmentation techniques[J]. Procedia Computer Science， 2015， 65： 797-806.