拉底过断层巷道中深孔爆破振动监测与分析
2021-06-06李争荣武鹏杰刘明武曹永冯兴隆王贻明
李争荣,武鹏杰 ,刘明武,曹永 ,冯兴隆,王贻明
(1.云南迪庆有色金属有限责任公司,云南 香格里拉市 674400;2.北京科技大学 金属矿山高效开采与安全教育部重点实验室,北京 100083;3.北京科技大学 土木与资源工程学院,北京 100083)
0 引言
矿山爆破施工期间,炸药爆炸产生的爆轰波瞬间作用在巷道围岩中形成强间断,并以爆源为中心、沿着巷道围岩等介质,以椭球状冲击波的形式向外扩散传播,伴随着传播距离的增大,冲击波能量迅速衰减而转化为波形较为平缓的应力波,引起巷道围岩质点振动,一旦超出安全允许范围,将导致其严重破坏。因此,为了得到爆破振动效应的衰减规律,对爆破振动进行系统的监测和研究是非常必要的。
针对爆破振动衰减规律的研究,国内外学者从20世纪初期开始做出大量研究。DOWDING[1]研究发现用介质质点位移作为爆破振动对围岩的破坏判据更符合实际。SLOBODAN Trajkovic等[2]学者讨论了如何确定爆破振动安全距离的问题,特别是研究了爆破振动效应对现场作业带来的不利影响。王先义等[3]提出了建立以质点振动速度峰值为主、振动波频谱和振动传播时间为辅的多参数安全判据。对于不同地质地形条件下的爆破振动衰减规律,也有学者进行了针对性的研究。张进平[4]指出,爆破受地质条件等因素的影响,导致爆破振动波在介质中传播的方向性以及质点振动峰速等值线的异向系数具有呈椭圆形分布的趋势。张永哲[5]通过对李家峡露天矿山爆破振动的监测与分析,发现爆破地震波在地表中传播通过断层后,大部分会出现主振频率降低、波形振动速度峰值降低的现象,但部分岩体也会出现波形主频增大的现象,说明断层对振动波的阻隔效应是复杂且非线性的。
上述研究主要通过现场试验和理论分析对爆破振动传播和衰减规律进行分析,虽已取得大量有价值的成果,但是对布置在断层破碎带附近的拉底巷道围岩的爆破振动效应研究较少,且得到的研究成果过于复杂,不利于生产应用。本文结合云南普朗铜矿地质概况,设计并实施拉底过断层中深孔爆破振动监测。通过对监测数据进行回归分析得到萨道夫斯基经验公式中的经验系数值K、α,进而获得装药量、速度、距离三者的关系,建立适用于现场地质条件的衰减规律公式,可为类似工程提供经验[6]。
1 工程概况
普朗铜矿位于滇西北迪庆藏族自治州东部,中甸县城50°方向、平距约36.4 km处[7]。普朗铜矿首采区地质构造复杂,除了大大小小的节理裂隙等构造面密集发育外,主要存在5条断层,还包括小断层若干,往往横穿多条穿脉或沿脉延伸几十米后尖灭。首采区主要断层详细情况见表1[8]。
普朗铜矿采用自然崩落法开采矿石,通过在3736m拉底水平进行中深孔拉底爆破,形成拉底空间,使上部矿体在次生应力场的作用下,内部不连续面持续扩张,并在矿石自重作用下进行崩落[9]。现场中深孔拉底爆破采用扇形中深孔炮孔,孔深3.5m~13m,根据首排炮孔设计参数,调整第2排、第3排炮孔的参数,形成交叉布置的炮孔结构,炮孔排距为1.9m。爆破炸药采用粒状铵油炸药,采用连续柱状装药结构,孔底、孔口双向起爆,起爆药包为1节Φ50mm乳化炸药。

表1 首采区主要断层特点(3760~3736m中段)
2 爆破振动监测
2.1 监测原理
中深孔爆破释放的能量在实现形成拉底空间目的的同时,有部分能量不可避免地以波的形式向四周传播并形成爆破地震波,炸药发生爆炸的整个过程是一个比较复杂的物理化学反应,同时也是一个能量转化以及传递的过程,而地震波在传播过程中不可避免地会对巷道围岩、支护体以及其他构筑物产生影响,即为爆破振动效应。根据岩石爆破的特性可知,爆破振动效应与质点振动速度的大小密切相关,在实际工程爆破中,往往采用振动速度峰值来衡量爆破振动效应,进而评估爆破振动的危害程度。为了确保构筑物的安全,必须对现场爆破质点振动速度加以监测。一般的爆破振动监测通常会将围岩物理力学参量的变化转换为电信号,通过电测法来记录围岩质点的物理力学性质改变,再对记录到的电信号进行转换与后处理,从而有效记录爆破振动的诸多参数[10]。
2.2 测点布置
本次现场爆破振动监测系统采用中科院成都分院自主研发的TC-4850爆破振动测振仪。为保证监测的可靠性,避免出现较大误差,该仪器设定采样率为8 kHz,采样时间为2 s,触发电平设置为0.2 cm/s,记录延时为−100ms。同时考虑到拉底巷道的地质条件,将爆破振动测振仪的传感器布置在距爆源2倍洞径的拉底巷道两帮上,且距底板1/3巷高,用石膏粉把三矢量传感器固定在基岩上形成刚性联结,分别监测测点水平径向、水平切向、垂直方向的质点振动速度。参考以往的监测经验及现场拉底巷道的布置情况,同时结合当前的拉底进度,此次共布置3个测点,要求每一处监测点至爆炸中心的距离按近密远疏的对数分布规律布置,因此设计每个测点至爆炸中心的距离依次为15m,30m,60m。现场测点布置如图1所示。

图1 测点布置
3 数据处理
3.1 试验结果
对拉底爆破展开多次振动监测后,把记录仪数据导入计算机,使用Blasting vibration analysis爆破振动分析软件处理数据。通过筛选对比,去掉误差较大的数据,选择其中较优的3组数据进行分析。相关振动数据以及相应的炸药量、爆心距等数据见表2。
由表2分析可得,在该拉底巷道所监测到的爆破振动主频频散现象比较明显,主频分布的频域跨度都比较大,几乎涵盖了从高到低的所有频率。可见爆破振动主频除了受到地震波传播距离和最大单响药量的影响外,拉底爆破现场的地形地质条件对频率的变化也均有影响。正是由于断层、节理裂隙等构造面的存在导致围岩传播介质的非线性,使得地震波频谱具有不规则的广谱性。

表2 爆破振动监测数据
3.2 回归分析
依据现有的研究成果,目前国内外一般采用萨道夫斯基经验公式对爆破振动监测数据进行回归分析。公式(1)中的K、α均是经验系数值,与爆破现场拉底巷道围岩的岩性条件相关,不同岩性条件下的K、α经验数据可参见表3。

表3 不同岩性条件下的K、α值
根据表2中的爆破振动速度及相对应的单段最大单响药量和爆心距,对萨氏公式进行二元线性拟合,以确定经验公式中的岩性系数K与α值,进而得到拉底过断层中深孔爆破作业的爆破振动衰减规律。

式中,V为围岩质点振动速度,cm/s;R为爆心距,即爆源与测点的直线距离,m;Q为爆破单段最大起爆药量,kg;K为与地质条件、围岩特性有关的岩性系数;α为爆破衰减系数。
将式(1)转化为一元线性回归公式
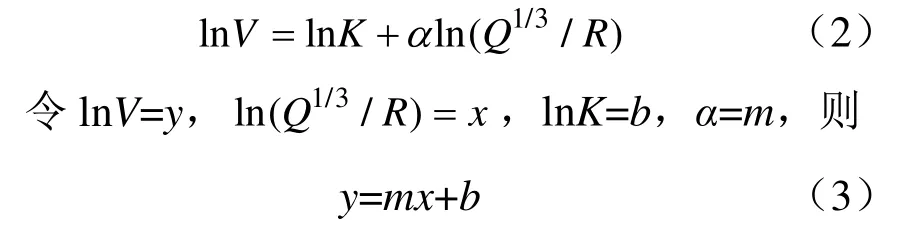
根据线形回归和最小二乘法的基本原理,使用Origin 2019软件拟合分析,得到本次测试的爆破振动衰减方程。三矢量和速度:
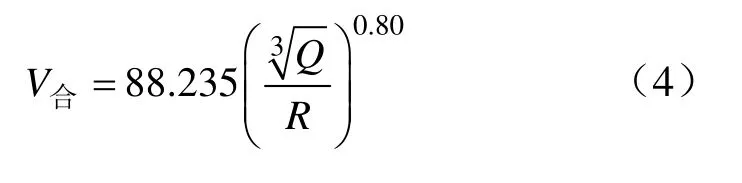
K=88.235,α=0.80,相关系数R2=0.932。
水平径向速度:

K=49.402,α=0.93,相关系数R2=0.897。
水平切向速度:

K= 61.559,α=0.89,相关系数R2=0.883。
垂直方向速度:

K=40.447,α=0.74,相关系数R2=0.927。
可得水平径向速度、水平切向速度、垂直方向速度、质点三矢量和速度与单段最大单响药量与爆心距比值的散点及线性回归图,见图2~图5。
由回归分析结果可知,拟合相关性系数较高,表明振动监测数据具有较高的可靠性,也进一步验证了公式(1)的合理性。根据表3对经验系数值的规定,发现萨氏公式适用于该矿山且经验系数K=88.235,α=0.80能真实地反映爆破振动波的衰减规律。
同时发现衰减系数α小于规定的阈值范围,α<1.3,衰减系数过小,表明质点振动速度受地质地形条件的影响,爆破振动影响范围变广、持续时间变长。这与现场实际情况相符,普朗铜矿地下有大大小小断层、破碎带,地震波在传播过程中遇到断层、节理裂隙面等结构面时,会产生折射和反射现象,此外,还会产生绕射等现象,使波的波形、频率和振动持续时间都发生变化。

图2 水平径向速度线性回归曲线

图3 水平切向速度线性回归曲线
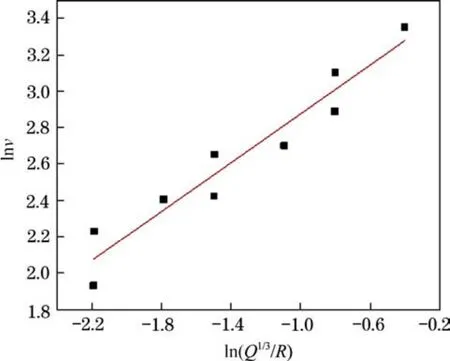
图4 垂直方向速度线性回归曲线

图5 三维合成速度线性回归曲线
4 结论
(1)由于拉底爆破施工现场地质地形条件的复杂性,且影响爆破振动衰减的因素不存在线性关系,因此对具体工程而言,应该通过现场监测,对数据进行拟合分析建立线性回归模型,从而得到符合现场地质地形条件的爆破振动衰减规律。
(2)试验区S5S拉底巷道爆破振动衰减系数K与α分别为88.235,0.80,即适用于现场的爆破振动传播数学模型为:与该区域岩性基本吻合,可以准确地反映爆破振动波在该区域的衰减规律。
(3)断层的存在导致中深孔拉底爆破振动效应影响范围变广、持续时间变长,对拉底巷道围岩及支护结构的破坏加剧。因此,后续的拉底爆破及类似工程,应及时优化爆破参数和支护巷道。
